Ce texte est destiné à ceux qui maîtrisent simplement la programmation. L'idée principale est de montrer étape par étape comment créer indépendamment le jeu à la
Wolfenstein 3D . Attention, je ne vais pas du tout rivaliser avec Carmack, c'est un génie et son code est magnifique. Je vis dans un endroit complètement différent: j'utilise l'énorme puissance de calcul des ordinateurs modernes pour que les étudiants puissent créer des projets amusants en quelques jours sans s'enliser dans la folie de l'optimisation. J'écris spécifiquement du code lent, car il est beaucoup plus court et plus facile à comprendre. Carmack
écrit 0x5f3759df , j'écris 1 / sqrt (x). Nous avons des objectifs différents.
Je suis convaincu qu'un bon programmeur n'est obtenu que de quelqu'un qui code à la maison pour le plaisir, et pas seulement assis à deux à l'université. Dans notre université, les programmeurs apprennent une série sans fin de toutes sortes de catalogues de bibliothèques et autres ennuis. Brr Mon objectif est de montrer des exemples de projets intéressants à programmer. C'est un cercle vicieux: s'il est intéressant de faire un projet, alors une personne y passe beaucoup de temps, acquiert de l'expérience et voit des choses encore plus intéressantes autour de lui (c'est devenu plus accessible!), Et encore une fois plonge dans un nouveau projet. C'est ce qu'on appelle la formation de projet, autour de bénéfices solides.
La feuille s'est avérée longue, j'ai donc divisé le texte en deux parties:
L'exécution de code à partir de mon référentiel ressemble à ceci:
Ce n'est pas un jeu fini, mais seulement un blanc pour les étudiants. Un exemple d'un jeu fini écrit par deux étudiants de première année, voir
la deuxième partie .
Il se trouve que je vous ai un peu trompé, je ne vous dirai pas comment faire un jeu complet en un week-end. Je n'ai fait qu'un moteur 3D. Les monstres ne me courent pas dessus et le personnage principal ne tire pas. Mais au moins j'ai écrit ce moteur en un samedi, vous pouvez vérifier l'historique des commits. En principe, les dimanches suffisent à rendre quelque chose de jouable, c'est-à-dire un week-end que vous pouvez rencontrer.
Au moment d'écrire ces lignes, le référentiel contient 486 lignes de code:
haqreu@daffodil:~/tinyraycaster$ cat *.cpp *.h | wc -l 486
Le projet dépend de SDL2, mais en général l'interface de la fenêtre et le traitement des événements depuis le clavier apparaissent assez tard,
à minuit samedi :), alors que tout le code de rendu a déjà été fait.
Donc, je décompose tout le code en étapes, en commençant par le compilateur C ++ nu. Comme dans mes précédents articles sur le planning (
tyts ,
tyts ,
tyts ), j'adhère à la règle «one step = one commit», car github facilite l'affichage de l'historique des changements de code.
Étape 1: enregistrer l'image sur le disque
Alors allons-y. Nous sommes encore très loin de l'interface de la fenêtre, pour commencer, nous allons simplement enregistrer les images sur le disque. Au total, nous devons être en mesure de stocker l'image dans la mémoire de l'ordinateur et de l'enregistrer sur le disque dans un format que certains programmes tiers comprendront. Je veux obtenir ce fichier:
 Voici le
Voici le code C ++ complet qui dessine ce dont nous avons besoin:
#include <iostream> #include <fstream> #include <vector> #include <cstdint> #include <cassert> uint32_t pack_color(const uint8_t r, const uint8_t g, const uint8_t b, const uint8_t a=255) { return (a<<24) + (b<<16) + (g<<8) + r; } void unpack_color(const uint32_t &color, uint8_t &r, uint8_t &g, uint8_t &b, uint8_t &a) { r = (color >> 0) & 255; g = (color >> 8) & 255; b = (color >> 16) & 255; a = (color >> 24) & 255; } void drop_ppm_image(const std::string filename, const std::vector<uint32_t> &image, const size_t w, const size_t h) { assert(image.size() == w*h); std::ofstream ofs(filename); ofs << "P6\n" << w << " " << h << "\n255\n"; for (size_t i = 0; i < h*w; ++i) { uint8_t r, g, b, a; unpack_color(image[i], r, g, b, a); ofs << static_cast<char>(r) << static_cast<char>(g) << static_cast<char>(b); } ofs.close(); } int main() { const size_t win_w = 512; // image width const size_t win_h = 512; // image height std::vector<uint32_t> framebuffer(win_w*win_h, 255); // the image itself, initialized to red for (size_t j = 0; j<win_h; j++) { // fill the screen with color gradients for (size_t i = 0; i<win_w; i++) { uint8_t r = 255*j/float(win_h); // varies between 0 and 255 as j sweeps the vertical uint8_t g = 255*i/float(win_w); // varies between 0 and 255 as i sweeps the horizontal uint8_t b = 0; framebuffer[i+j*win_w] = pack_color(r, g, b); } } drop_ppm_image("./out.ppm", framebuffer, win_w, win_h); return 0; }
Si vous n'avez pas de compilateur à portée de main, cela n'a pas d'importance, si vous avez un compte sur un github, vous pouvez voir ce code, le modifier et l'exécuter (sic!) En un clic directement depuis le navigateur.

En suivant ce lien, gitpod créera une machine virtuelle pour vous, lancera VS Code et ouvrira un terminal sur la machine distante. Dans l'historique des commandes du terminal (cliquez sur la console et appuyez sur la flèche vers le haut), il existe déjà un ensemble complet de commandes qui vous permettent de compiler le code, de l'exécuter et d'ouvrir l'image résultante.
Donc, ce que vous devez comprendre de ce code. Tout d'abord, les couleurs que je stocke dans un type entier à quatre octets uint32_t. Chaque octet est un composant de R, G, B ou A. Les fonctions pack_color () et unpack_color () vous permettent d'accéder aux composants individuels de chaque couleur.
La deuxième image bidimensionnelle que je stocke dans le tableau unidimensionnel habituel. Pour arriver au pixel avec les coordonnées (x, y) je n'écris pas l'image [x] [y], mais j'écris l'image [x + y * largeur]. Si cette méthode de regroupement d'informations bidimensionnelles dans un tableau unidimensionnel est nouvelle pour vous, saisissez dès maintenant un stylo et traitez-le. Pour moi personnellement, cette étape n'atteint même pas le cerveau, elle est traitée directement dans la moelle épinière. Les tableaux tridimensionnels et plus dimensionnels peuvent être emballés exactement de la même manière, mais nous ne dépasserons pas les deux composants.
Ensuite, je parcours ma photo dans un double cycle simple, la remplis d'un dégradé et l'enregistre sur le disque au format .ppm.
Étape 2: dessinez une carte de niveau
Nous avons besoin d'une carte de notre monde. À ce stade, je veux simplement déterminer la structure des données et dessiner une carte à l'écran. Cela devrait ressembler à ceci:

Les changements que
vous pouvez voir ici . Tout y est simple: j'ai codé en dur la carte en un tableau unidimensionnel de caractères, défini la fonction de dessiner un rectangle et parcouru la carte en dessinant chaque cellule.
Je vous rappelle que ce bouton lancera le code à ce stade:

Étape 3: ajouter un joueur
De quoi avons-nous besoin pour dessiner un joueur sur la carte? Les coordonnées GPS suffisent :)
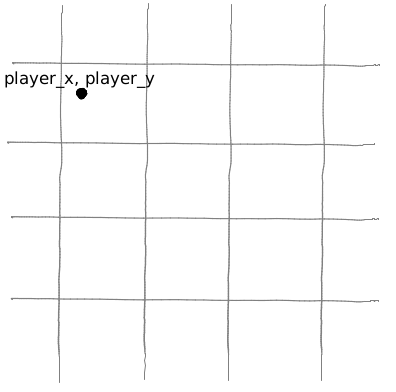
Ajoutez deux variables x et y et dessinez le joueur à l'endroit approprié:

Les changements que
vous pouvez voir ici . À propos de gitpod, je ne m'en souviendrai plus :)

Étape 4: aka trace de premier rayon du télémètre virtuel
En plus des coordonnées du joueur, ce serait bien de savoir dans quelle direction il regarde. Par conséquent, nous ajoutons une autre variable player_a, qui donne la direction du regard du joueur (l'angle entre la direction du regard et l'axe des abscisses):

Et maintenant je veux pouvoir glisser le long du rayon orange. Comment faire Extrêmement simple. Regardons un triangle vert à droite. Nous savons que cos (player_a) = a / c, et que sin (player_a) = b / c.

Que se passe-t-il si je prends arbitrairement c (positif) et compte x = player_x + c * cos (player_a) et y = player_y + c * sin (player_a)? Nous nous retrouverons au point violet; en faisant varier le paramètre c de zéro à l'infini, on peut faire glisser ce point violet le long de notre rayon orange, et c est la distance de (x, y) à (player_x, player_y)!
Le cœur de notre moteur graphique est ce cycle:
float c = 0; for (; c<20; c+=.05) { float x = player_x + c*cos(player_a); float y = player_y + c*sin(player_a); if (map[int(x)+int(y)*map_w]!=' ') break; }
On déplace le point (x, y) le long du rayon, s'il rencontre un obstacle sur la carte, alors on termine le cycle, et la variable c donne la distance à l'obstacle! Qu'est-ce qui n'est pas un télémètre laser?

Les changements que
vous pouvez voir ici .

Étape 5: Aperçu du secteur
Un faisceau est très bien, mais nos yeux voient toujours tout un secteur. Appelons l'angle de vue fov (champ de vision):

Et libérons 512 rayons (au fait, pourquoi 512?), Balayant en douceur tout le secteur de visionnement:
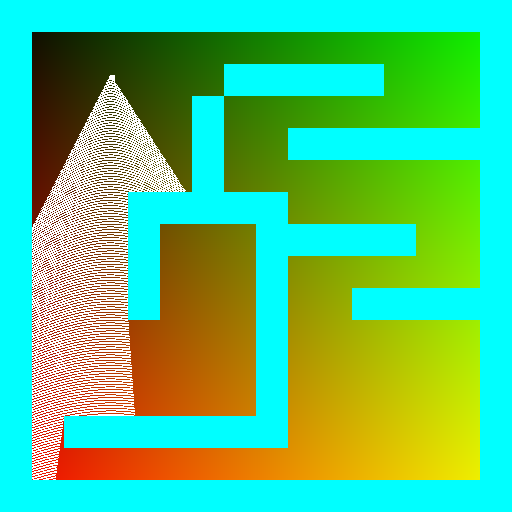
Les changements que
vous pouvez voir ici .

Étape 6: 3D!
Et maintenant le point clé. Pour chacun des 512 rayons, nous avons obtenu la distance de l'obstacle le plus proche, non? Et maintenant, faisons une deuxième image de 512 pixels de large (spoiler); dans lequel pour chaque rayon, nous dessinerons un segment vertical, et la hauteur du segment est inversement proportionnelle à la distance à l'obstacle:

Encore une fois, c'est la clé pour créer l'illusion 3D, assurez-vous de bien comprendre ce qui est en jeu. En dessinant des segments verticaux, en fait, nous dessinons une clôture de piquetage, où la hauteur de chaque piquet est la plus petite, la plus éloignée de nous:

Les changements que
vous pouvez voir ici .

Étape 7: Première animation
À ce stade, pour la première fois, nous dessinons quelque chose de dynamique (je viens de déposer 360 photos sur le disque). Tout est trivial: je change player_a, dessine une image, sauvegarde, change player_a, tire, sauvegarde. Pour le rendre un peu plus amusant, j'ai attribué une valeur de couleur aléatoire à chaque type de cellule de notre carte.
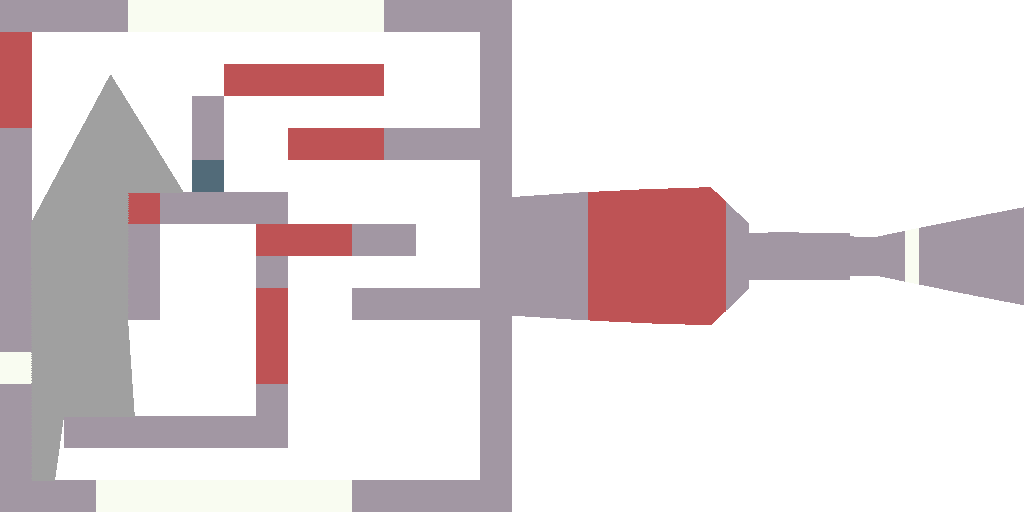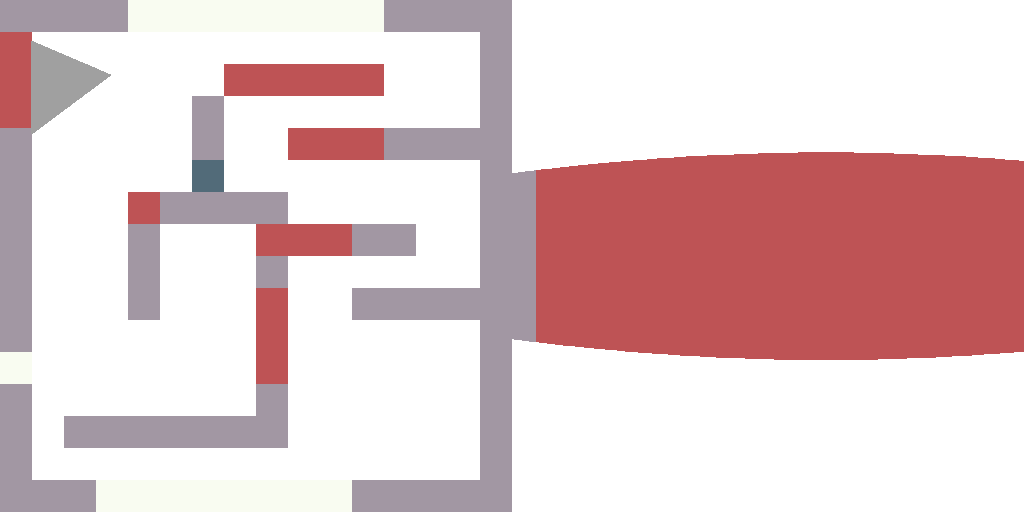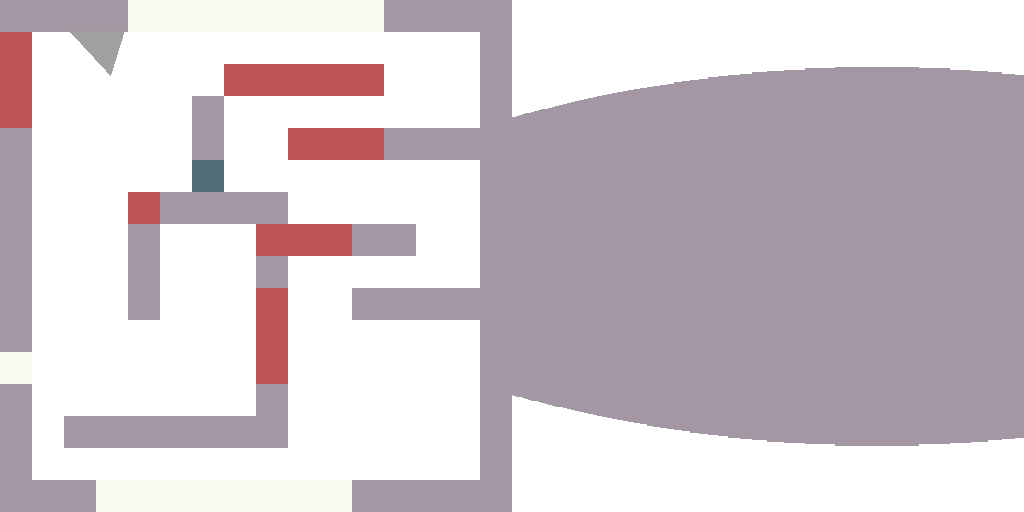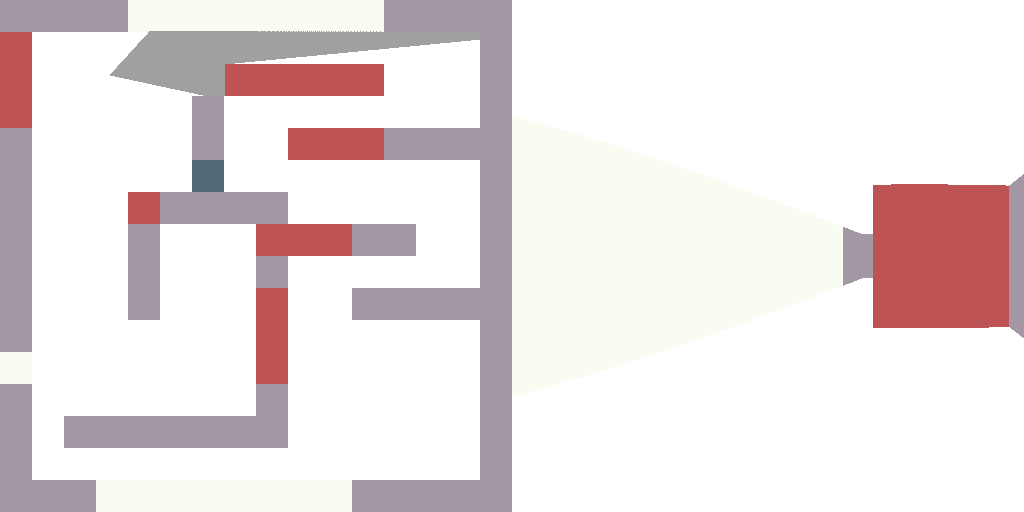
Les changements que
vous pouvez voir ici .

Étape 8: correction des yeux de poisson
Avez-vous remarqué quel grand effet fish-eye nous obtenons lorsque nous regardons un mur de près? Cela ressemble à ceci:

Pourquoi? Oui, très simple. Ici, nous regardons le mur:

Pour dessiner notre mur, nous mettons en lumière notre secteur bleu avec un rayon violet. Prenez la valeur spécifique de la direction du faisceau, comme dans cette image. La longueur du segment orange est nettement inférieure à la longueur du violet. Puisque pour déterminer la hauteur de chaque segment vertical que nous dessinons sur l'écran, nous divisons par la distance à l'obstacle, le fisheye est assez naturel.
Pour corriger cette distorsion n'est pas difficile du tout,
regardez comment cela se fait . Assurez-vous de bien comprendre d'où vient le cosinus. Dessiner un diagramme sur un morceau de papier aide beaucoup.


Étape 9: charger le fichier de texture
Il est temps de gérer les textures. Je suis paresseux pour écrire moi-même un téléchargeur d'images, j'ai donc pris l'excellente
bibliothèque stb . J'ai préparé un fichier avec des textures pour les murs, toutes les textures sont carrées et emballées horizontalement dans l'image:

À ce stade, je charge simplement les textures en mémoire. Pour tester le code écrit, je dessine simplement comme c'est la texture avec l'index 5 dans le coin supérieur gauche de l'écran:

Les changements que
vous pouvez voir ici .

Étape 10: utilisation rudimentaire des textures
Maintenant, je jette des couleurs générées de manière aléatoire et teinte mes murs en prenant le pixel supérieur gauche de la texture correspondante:
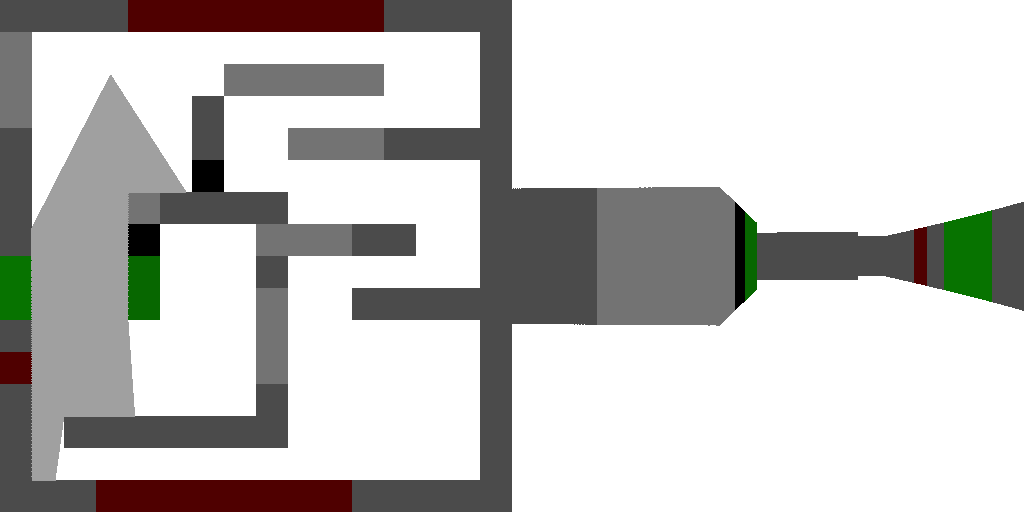
Les changements que
vous pouvez voir ici .

Étape 11: texturer les murs pour de vrai
Et maintenant, le moment tant attendu est venu où nous voyons enfin les murs de briques:

L'idée de base est très simple: ici, nous glissons le long du rayon actuel et nous nous arrêtons au point x, y. Supposons que nous nous sommes installés sur un mur «horizontal», alors y est presque entier (pas vraiment, car notre façon de se déplacer le long du rayon introduit une petite erreur). Prenons la partie fractionnaire de x et appelons-la hitx. La partie fractionnaire est inférieure à un, par conséquent, si nous multiplions hitx par la taille de la texture (j'en ai 64), cela nous donnera la colonne de texture qui doit être dessinée à cet endroit. Il reste à l'étirer à la bonne taille et la chose est dans le chapeau:

En général, l'idée est extrêmement primitive, mais nécessite une exécution minutieuse, car nous avons également des murs «verticaux» (ceux avec hitx proche de zéro [x entier]). Pour eux, la colonne de texture est déterminée par hity, la partie fractionnaire de y. Les changements que
vous pouvez voir ici .

Étape 12: il est temps de refactoriser!
A ce stade, je n'ai rien fait de nouveau, je viens de commencer le nettoyage général. Jusqu'à présent, j'avais un gigantesque fichier (185 lignes!), Et il devenait difficile de travailler dessus. Par conséquent, je l'ai divisé en un nuage de petits, malheureusement, en passant, doublant presque la taille du code (319 lignes), sans ajouter aucune fonctionnalité. Mais ensuite, il est devenu beaucoup plus pratique à utiliser, par exemple, pour générer une animation, il suffit de faire une telle boucle:
for (size_t frame=0; frame<360; frame++) { std::stringstream ss; ss << std::setfill('0') << std::setw(5) << frame << ".ppm"; player.a += 2*M_PI/360; render(fb, map, player, tex_walls); drop_ppm_image(ss.str(), fb.img, fb.w, fb.h); }
Eh bien, voici le résultat:
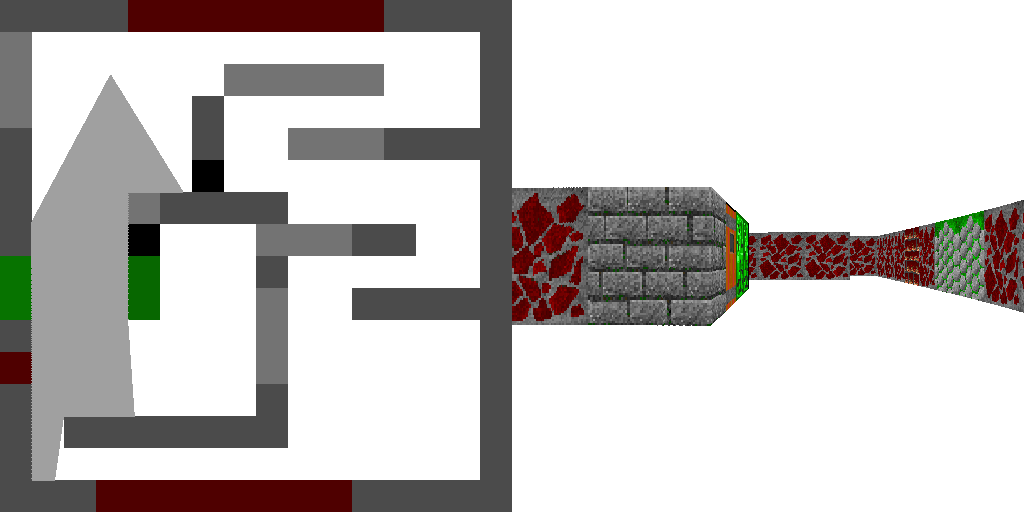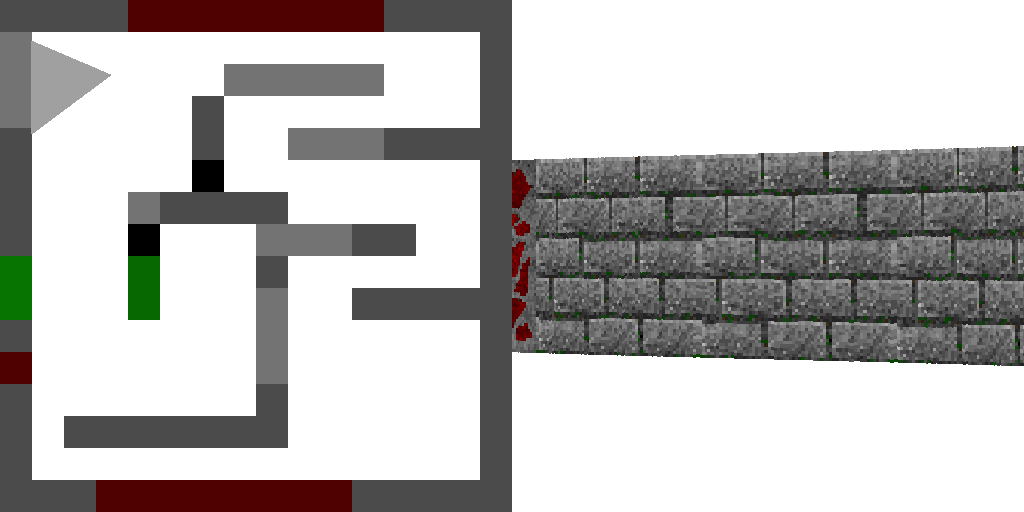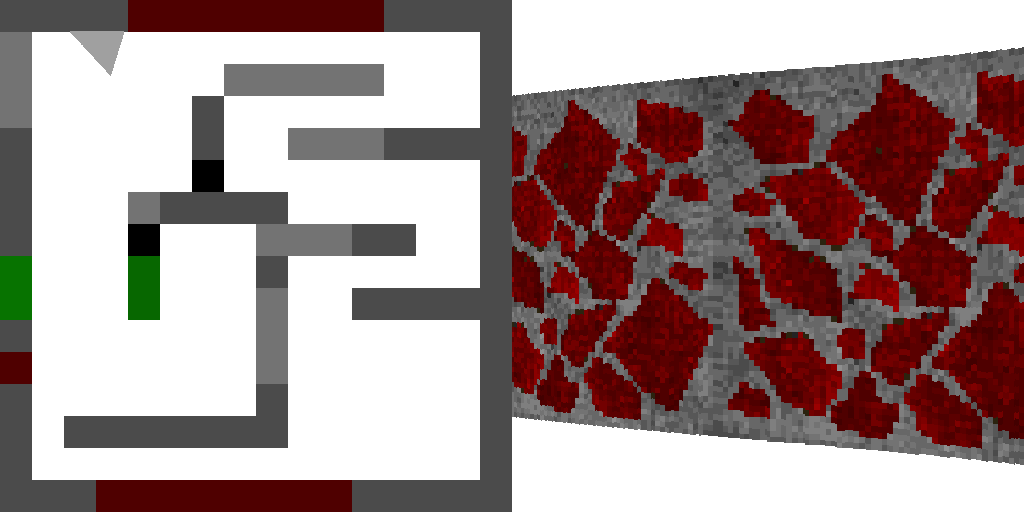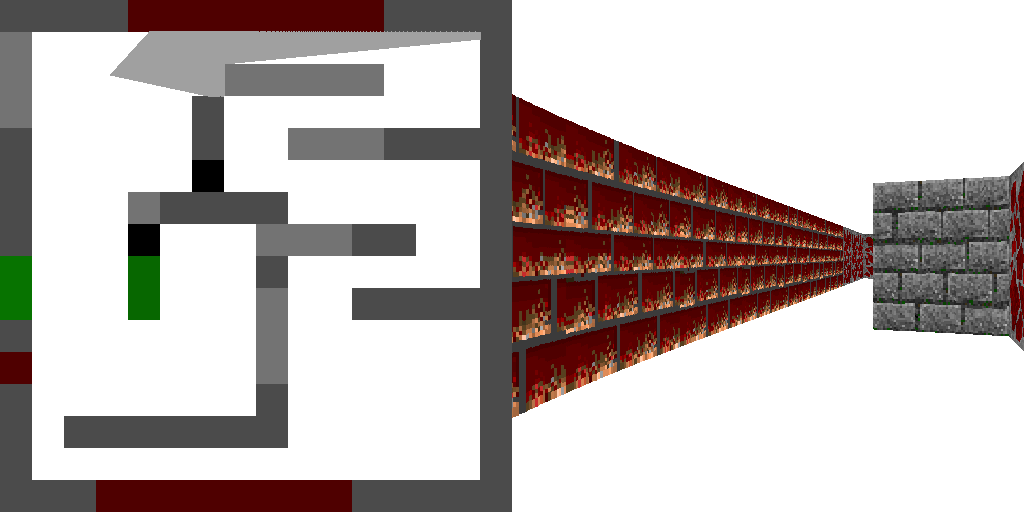
Les changements que
vous pouvez voir ici .

À suivre ... immédiatement
Sur cette note optimiste, je termine la moitié actuelle de ma feuille, la seconde moitié
est disponible ici . Nous y ajouterons des monstres et un lien vers SDL2 afin que vous puissiez vous promener dans notre monde virtuel.