Julia et la méthode de descente de coordonnées

La méthode de descente coordonnée est l'une des méthodes les plus simples d'optimisation multidimensionnelle et fait un bon travail pour trouver un minimum local de fonctions avec une topographie relativement lisse, il est donc préférable de commencer à vous familiariser avec les méthodes d'optimisation.

La recherche de l'extremum s'effectue dans la direction des axes de coordonnées, c'est-à-dire pendant le processus de recherche, une seule coordonnée est modifiée. Ainsi, le problème multidimensionnel est réduit à unidimensionnel.

Algorithme

Premier cycle:

• $$$x_1 = var$, $$$x_2 = x_2 ^ 0$, $$$x_3 = x_3 ^ 0$, ..., $$$x_n = x_n ^ 0$.
• Recherche de fonctions extremum $$$f (x_1)$. Mettre l'extremum de la fonction au point $$$x_1 ^ 1$.
• $$$x_1 = x_1 ^ 1$, $$$x_2 = var$, $$$x_3 = x_3 ^ 0$, ..., $$$x_n = x_n ^ 0$. Fonction Extremum $$$f (x_2)$est égal à $$$x_2 ^ 1$
• ...
• $$$x_1 = x_1 ^ 1$, $$$x_2 = x_2 ^ 1$, $$$x_3 = x_3 ^ 1$, ..., $$$x_n = var$.
  À la suite de l'exécution de n étapes, un nouveau point d'approche de l'extremum a été trouvé $$$(x_1 ^ 1, x_2 ^ 1, ..., x_n ^ 1)$. Ensuite, nous vérifions le critère de fin de compte: s'il est rempli, la solution est trouvée, sinon nous effectuons un cycle de plus.

La préparation

Vérifiez les versions du package:

(v1.1) pkg> status Status `C:\Users\User\.julia\environments\v1.1\Project.toml` [336ed68f] CSV v0.4.3 [a93c6f00] DataFrames v0.17.1 [7073ff75] IJulia v1.16.0 [47be7bcc] ORCA v0.2.1 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.3 [91a5bcdd] Plots v0.23.0 [ce6b1742] RDatasets v0.6.1 [90137ffa] StaticArrays v0.10.2 [8bb1440f] DelimitedFiles [10745b16] Statistics 

Nous définissons une fonction pour dessiner les lignes de surface ou de niveau dans laquelle il serait pratique d'ajuster les limites du graphique:

 using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end 

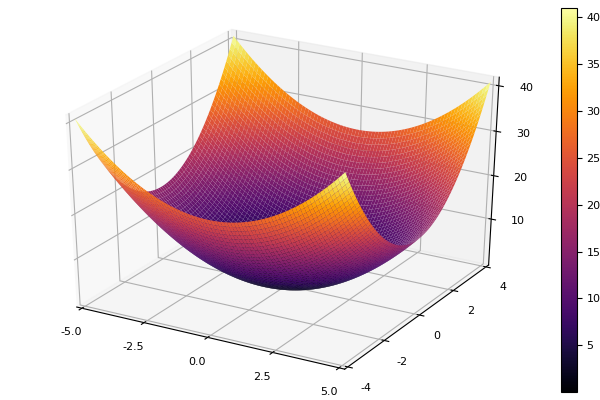
En tant que fonction modèle, nous choisissons un paraboloïde elliptique

 parabol(x) = sum(u->u*u, x) fun = parabol plotter(surface, low = [-1 -1], up = [1 1]) 

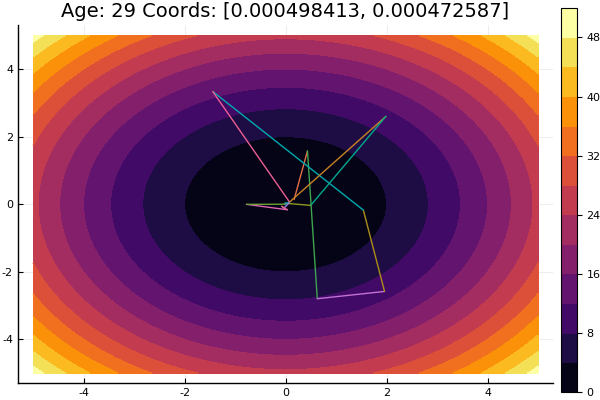
Descente coordonnée

Nous implémentons la méthode dans une fonction qui prend le nom de la méthode d'optimisation unidimensionnelle, la dimension du problème, l'erreur souhaitée, l'approximation initiale et les restrictions pour tracer des lignes de niveau. Tous les paramètres sont définis sur les valeurs par défaut.

 function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1]) k = 1 #      sumx = 0 sumz = 1 plotter(contour, low = low, up = up) #    x = [ fit[1] ] #     y = [ fit[2] ] #      while abs(sumz - sumx) > ε && k<80 fitz = copy(fit) for i = 1:ndimes odm(i, fit, ε) #    end push!(x, fit[1]) push!(y, fit[2]) sumx = sum(abs, fit ) sumz = sum(abs, fitz) #println("$k $fit") k += 1 end #     scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# , ,  p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))") end 

Ensuite, nous allons essayer différentes méthodes d'optimisation unidimensionnelle.

La méthode de Newton

$$

$$x_ {n + 1} = x_n - \ frac {f (x_n)} {f '(x_n)}$$

L'idée de la méthode est simple tout comme l'implémentation

 #  dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1] function newton2(i, fit, ϵ) k = 1 oldfit = Inf while ( abs(fit[i] - oldfit) > ϵ && k<50 ) oldfit = fit[i] tryfit = fun(fit) / dfun(fit, i) fit[i] -= tryfit println(" $k $fit") k+=1 end end ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

Newton est assez exigeant sur l'approximation initiale, et sans limitation sur les marches, il peut facilement rouler à des distances inconnues. Le calcul de la dérivée est souhaitable, mais vous pouvez vous en tirer avec une petite variation. Nous modifions notre fonction:

 function newton(i, fit, ϵ) k = 1 oldfit = Inf x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) while ( abs(oldfit - fit[i]) > ϵ && k<50 ) fx = fun(fit) oldfit = fit[i] fit[i] += 0.01 dfx = fun(fit) fit[i] -= 0.01 tryfit = fx*0.01 / (dfx-fx) #        if( abs(tryfit) > abs(fit[i])*10 ) push!(x, fit[1]) push!(y, fit[2]) break end fit[i] -= tryfit #println(" $k $fit") push!(x, fit[1]) push!(y, fit[2]) k+=1 end #  - -   plot!(x, y, w = 3, legend = false, marker = :rect ) end ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

Interpolation parabolique inverse

Une méthode qui ne nécessite pas de connaissance du dérivé et qui a une bonne convergence

 function ipi(i, fit, ϵ) # inverse parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.15 xn[i] = fit[i] + 0.15 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<80 fn = fun(xn) a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) ) b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) ) c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) ) xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i] xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4]) 

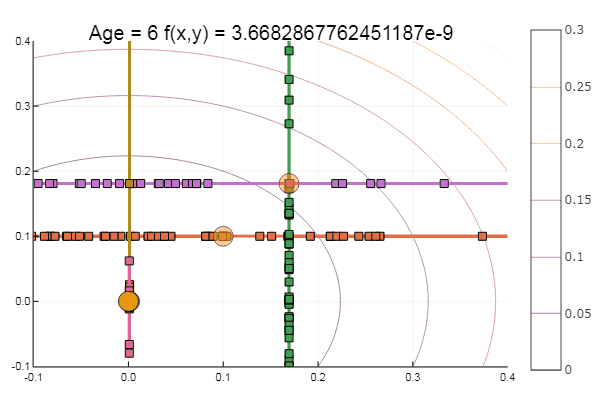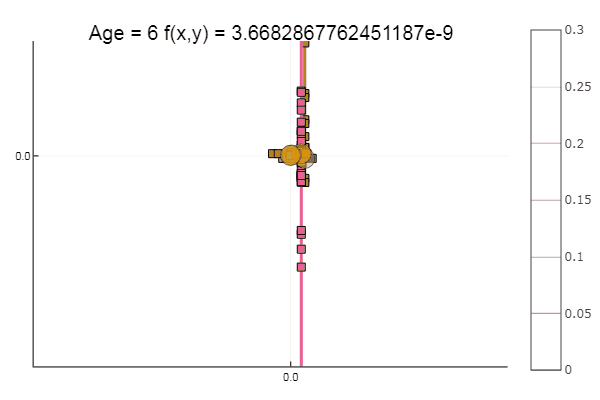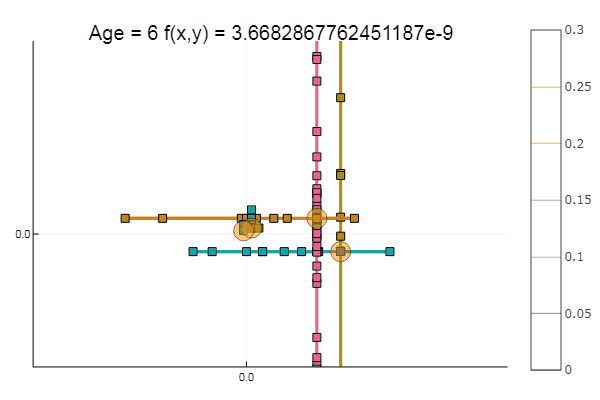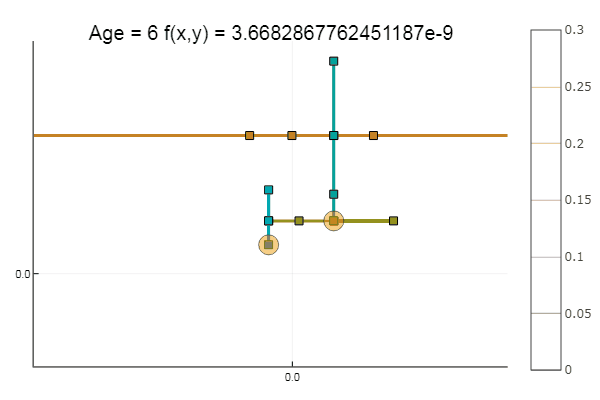
Si l'on aggrave l'approximation initiale, la méthode commencera à nécessiter un nombre immense d'étapes pour chaque époque de descente de coordonnées. À cet égard, son frère gagne

Interpolation parabolique séquentielle

Il nécessite également trois points de départ , mais sur de nombreuses fonctions de test, il donne des résultats plus satisfaisants.

 function spi(i, fit, ϵ) # sequential parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.01 xn[i] = fit[i] + 0.01 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<200 fn = fun(xn) v0 = xn1[i] - xn2[i] v1 = xn[i] - xn2[i] v2 = xn[i] - xn1[i] s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i] s1 = xn[i] *xn[i] - xn2[i]*xn2[i] s2 = xn[i] *xn[i] - xn1[i]*xn1[i] xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0) xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4]) 

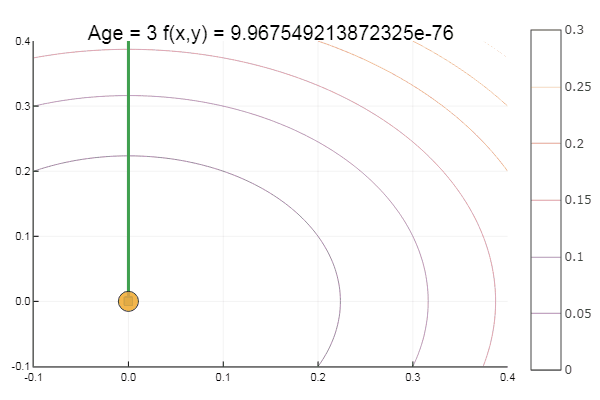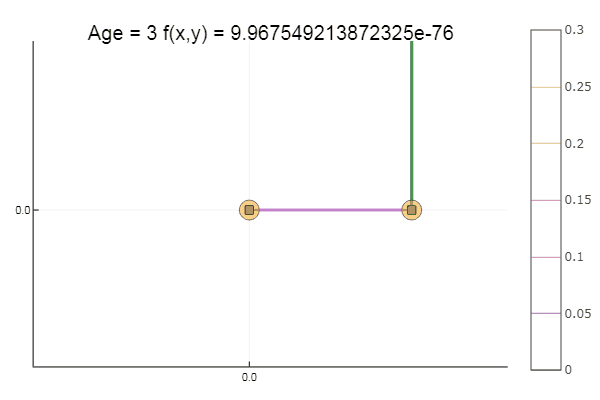
Sortir d'un point de départ très merdique s'est fait en trois étapes! Bon ... Mais toutes les méthodes ont un inconvénient - elles convergent vers un minimum local. Prenons maintenant la fonction d'Ackley pour la recherche

$$

$$f (x, y) = - 20 \ exp \ left [-0.2 {\ sqrt {0.5 \ left (x ^ {2} + y ^ {2} \ right)}} \ right] - \ exp \ left [ 0,5 \ gauche (\ cos 2 \ pi x + \ cos 2 \ pi y \ droite) \ droite] + e + 20$$

 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly plotter(surface, low = [-5 -5], up = [5 5]) 

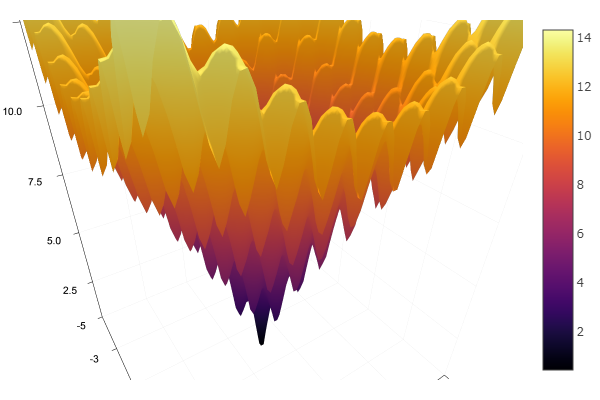
 ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4]) 

Méthode du ratio d'or

Théorie Bien que l'implémentation soit compliquée, la méthode se montre parfois bien en sautant les minima locaux

 function interval(i, fit, st) d = 0. ab = zeros(2) fitc = copy(fit) ab[1] = fitc[i] Fa = fun(fitc) fitc[i] -= st Fdx = fun(fitc) fitc[i] += st if Fdx < Fa st = -st end fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) while Fb < Fa d = ab[1] ab[1] = ab[2] Fa = Fb fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) # println("----", Fb, " ", Fa) end if st < 0 c = ab[2] ab[2] = d d = c end ab[1] = d ab end function goldsection(i, fit, ϵ) ϕ = Base.MathConstants.golden ab = interval(i, fit, 0.01) α = ϕ*ab[1] + (1-ϕ)*ab[2] β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = α Fa = fun(fit) fit[i] = β Fb = fun(fit) while abs(ab[2] - ab[1]) > ϕ if Fa < Fb ab[2] = β β = α Fb = Fa α = ϕ*ab[1] + (1-ϕ)*ab[2] fit[i] = α Fa = fun(fit) else ab[1] = α α = β Fa = Fb β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = β Fb = fun(fit) end println(">>>", i, ab) plot!(ab, w = 1, legend = false, marker = :rect ) end fit[i] = 0.5(ab[1] + ab[2]) end ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.]) 

C’est tout avec une descente coordonnée. Les algorithmes des méthodes présentées sont assez simples, il n'est donc pas difficile de les implémenter dans votre langue préférée. À l'avenir, vous pouvez envisager les outils intégrés du langage Julia , mais pour l'instant, vous voulez tout ressentir avec vos mains, pour ainsi dire, envisager des méthodes plus compliquées et plus efficaces, puis vous pouvez passer à l'optimisation globale, en comparant simultanément avec la mise en œuvre dans une autre langue.

Littérature

1. Zaitsev V.V. Méthodes numériques pour les physiciens. Equations non linéaires et optimisation: un tutoriel. - Samara, 2005 - 86s.
2. Ivanov A.V. Méthodes informatiques pour l'optimisation des systèmes optiques. Guide d'étude. –SPb: SPbSU ITMO, 2010 - 114s.
3. Popova T. M. Méthodes d'optimisation multidimensionnelle: lignes directrices et tâches pour les travaux de laboratoire dans la discipline "Méthodes d'optimisation" pour les étudiants de la direction "Mathématiques Appliquées" / comp. T. M. Popova. - Khabarovsk: maison d'édition du Pacifique. état Université, 2012 .-- 44 p.