Comment fonctionnent réellement les indicateurs techniques en bourse?

Quiconque a déjà été intéressé par les actions ou les crypto-monnaies a vu ces lignes supplémentaires sur les graphiques. Vous avez peut-être entendu l'opinion selon laquelle cela ne fonctionne pas. Mais ils améliorent considérablement ma capacité de trading, tout en affichant de nombreuses données importantes. Mais comment fonctionnent-ils réellement? Et à qui cela peut être utile?

Vous devriez certainement lire ceci si:

1. Vous les utilisez dans le day trading
2. Vous envisagez d'écrire un bot de trading
3. Si vous souhaitez mettre en place vous-même une stratégie ou des indicateurs de trading

Le plus souvent, les indicateurs techniques sont une fonction de fenêtre, une fonction récursive ou une fonction pondérée des prix / volumes tirée de la bourse au format UOHLCV (heure unix, ouverture, haut, bas, fermeture, volume). Il n'est pas rare que les indicateurs utilisent différents filtrages, minimums et maximums ou d'autres indicateurs comme base pour les calculs ultérieurs.

Moyenne mobile simple (SMA)

Lors du codage des indicateurs, il est très pratique d'utiliser une approche fonctionnelle. Par exemple, la moyenne mobile est juste la moyenne de chaque valeur de la fenêtre mobile.

function sma($close, window) { return rolling(x => mean(x), window, $close); } 

où la moyenne est l'opération qui calcule la moyenne du tableau et le roulement est la combinaison de la fonction de fenêtre qui, pour chaque élément existant dans le tableau, produit un tableau des n derniers éléments et l' opération qui plie cette fenêtre en un nombre.

 function rolling(operation, window, array) { let result = []; for (let i = 0; i < array.length; i++) { if (i + 1 < window) { result.push(NaN); } else { result.push(operation(array.slice(i + 1 - window, i + 1))); } } return result; } 

Le SMA est un indicateur en retard et permet de déterminer la tendance. Il est dessiné en superposition sur le graphique et les premières valeurs sont généralement supprimées. Deux moyennes mobiles peuvent être utilisées ensemble pour générer des signaux de croisement.



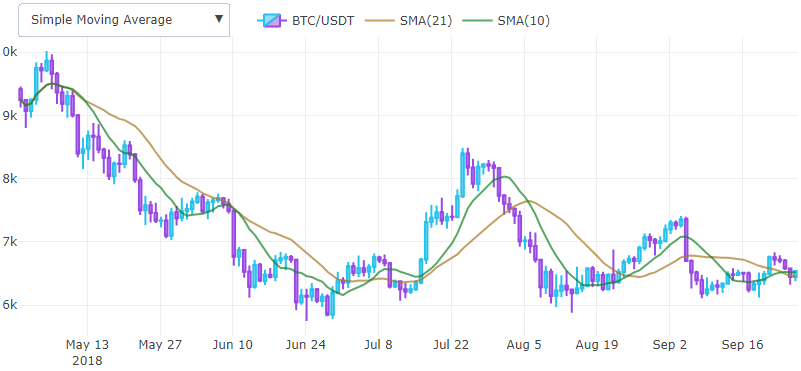
Un croisement haussier se produit lorsqu'une moyenne mobile relativement courte éclate la moyenne mobile longue. La moyenne mobile à pondération exponentielle est plus souvent utilisée dans la pratique, car une fonction de fenêtre pondérée réduit l'effet de retard.

Écart type (STDEV)

Si nous remplaçons la fonction moyenne dans SMA par l'écart-type, nous obtiendrons un écart-type glissant

 function stdev($close, window) { return rolling(x => sd(x), window, $close); } 

Où sd est considéré comme la racine carrée de la variance et généralement sans correction de Bessel. Nous supposerons que tout le monde comprend comment implémenter sd

$$

$$sd (x) = \ sqrt {\ frac {\ sum (x_i- \ hat x) ^ 2} {N}}.$$

La racine carrée de la variance est utilisée parce que la variance elle-même mesurée en dollars suqare en termes de théorie des dimensions et non parce que quelqu'un a déposé une marque ou quoi que ce soit.

Bandes de Bollinger (BBAND)

Ainsi, nous avons déjà mis en place deux indicateurs de base que nous pouvons combiner et en obtenir de nouveaux. Par exemple, si nous considérons l'ajout ponctuel de la moyenne mobile et de l'écart-type multiplié par 2, nous obtiendrons la partie supérieure de la bande de Bollinger et la partie inférieure que nous obtiendrons si nous soustrayons.

 function bb($close, window, mult) { let middle = sma($close, window); let upper = pointwise((a, b) => a + b * mult, middle, stdev($close, window)); let lower = pointwise((a, b) => a - b * mult, middle, stdev($close, window)); return { lower : lower, upper : upper}; } 

où la fonction point par point est une autre fonction utile

 export function pointwise(operation, ...arrays) { let result = []; for (let i = 0, len = arrays[0].length; i < len; i++) { let iarr = (i) => arrays.map(x => x[i]); result[i] = operation(...iarr(i)); } return result; } 

et il suffit d'effectuer une opération avec plusieurs tableaux



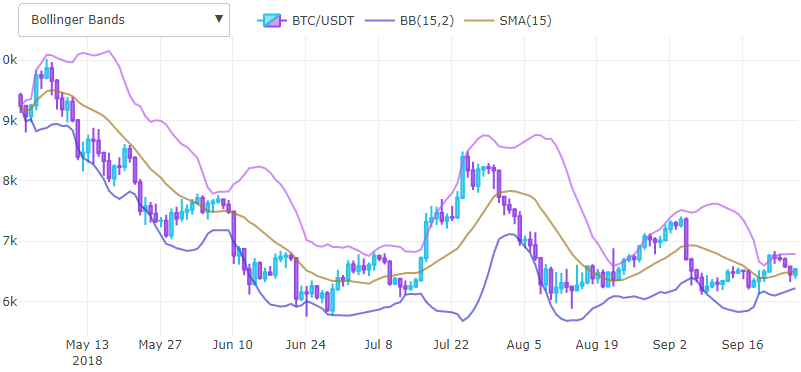
Les bandes de Bollinger aident à déterminer le calme avant le mouvement des grands prix et sont utilisées comme un outil pour déplacer la volatilité directement sur le graphique, l'écart-type soustrait / ajouté de la moyenne mobile afin d'être affiché en superposition sur un graphique avec le prix.

Moyenne mobile exponentielle (EMA)

Comment réduire le décalage de la moyenne mobile simple? Puisqu'il calcule la moyenne des n derniers cours de clôture, nous pouvons comprendre que nous pouvons effectuer la sommation avec un certain poids et réduire la contribution des anciens prix.

$$

$$\ bar x = \ frac {\ sum x_i} {N} = \ frac {\ sum 1 \ cdot x_i} {\ sum 1} \ quad \ Rightarrow \ quad \ widetilde {x} = \ frac {\ sum x_i w_i } {\ sum w_i}$$

Par exemple, si nous choisissons $$$w_n = q ^ n$et une constante $$$q$c'est moins d'un, alors nous obtenons un poids infiniment décroissant, si nous ajoutons les prix en commençant par le plus récent.



Il est également possible d'approximer les calculs et d'obtenir une équation récursive si nous développons la fenêtre sur toute sa longueur et supposons que la contribution des queues est faible.

$$

$$1 + q + q ^ 2 + ... + q ^ n \ underset {n \ to \ infty} {\ underset {q <0} {=}} \ frac {1} {1-q} \\ \ mathrm {EMA} _ {curr} = \ frac {\ sum x_i q ^ i} {\ sum q ^ i} = (1-q) \ sum x_i q ^ i \\ \ mathrm {EMA} _ {next} = \ frac {x_ {suivant} + q \ cdot \ sum x_i q ^ i} {1 + q \ cdot \ sum q ^ i} = (1-q) \ cdot \ left [x_ {suivant} + q \ cdot \ sum x_i q ^ i \ right] \\ \ mathrm {EMA} _ {next} = (1-q) \ cdot x_ {next} + q) \ cdot \ mathrm {EMA} _ {curr}$$

Enfin, nous avons besoin d'une valeur α = 1 - q comme constante de lissage. Il est possible de prouver que lorsque nous choisissons $$$\ alpha = 2 / (N + 1)$Le centre de masse des tableaux de poids EMA et SMA ci-dessus devient égal. Dans le code, cela semble beaucoup plus simple.

 function ema($close, window, weight = null) { weight = weight ? weight : 2 / (window + 1); let ema = [ mean($close.slice(0, window)) ]; for (let i = 1; i < $close.length; i++) { ema.push($close[i] * weight + ema[i - 1] * (1 - weight)); }; return ema; } 

En général, c'est la même moyenne mobile mais plus sensible.


L'efficacité de l'utilisation dépend de votre expérience et des paramètres utilisés. Par exemple sur ce site les paramètres sont assez bien choisis.

Divergence de convergence moyenne mobile (MACD)

Gerald Appel en 1979 a proposé l'un des indicateurs les plus simples et les plus efficaces disponibles. Il transforme deux indicateurs de tendance EMA en oscillateur de momentum et offre le meilleur des deux mondes: suivi de tendance et momentum. En gros, l'histogramme MACD est un dérivé du prix. Il est dessiné dans un nouveau système de coordonnées plutôt qu'une superposition et il représente avec deux lignes et un histogramme.



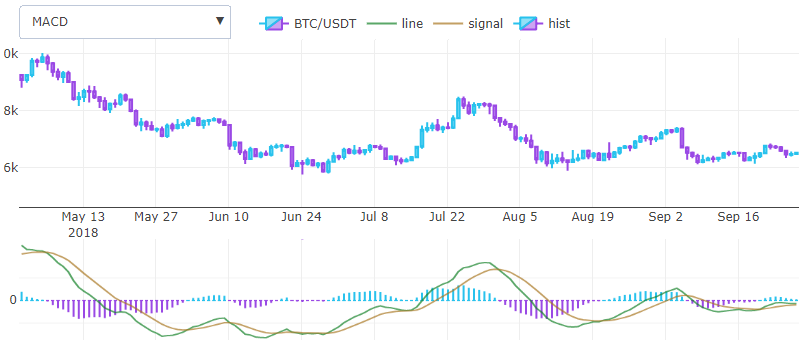
Pour calculer la ligne MACD, nous devons soustraire EMA long de court, c'est tout. Un autre EMA de cette ligne avec une petite fenêtre produira la ligne de signal. L'histogramme est obtenu par différence entre les deux résultats précédents.

 function macd($close, wshort, wlong, wsig) { let line = pointwise((a, b) => a - b, ema($close, wshort), ema($close, wlong)); let signal = ema(line, wsig); let hist = pointwise((a, b) => a - b, line, signal); return { line : line, signal : signal, hist : hist }; } 

Matrice de corrélation

Si vous vous intéressez à l'investissement à long terme et à l'analyse de portefeuille, vous trouverez la matrice de corrélation utile.

 function cor(f, g) { let Ef = mean(f), Eg = mean(g); let Ef2 = mean(pointwise((a) => a * a, f)); let Eg2 = mean(pointwise((a) => a * a, g)); let Efg = mean(pointwise((a, b) => a * b, f, g)); return (Efg - Ef * Eg) / Math.sqrt((Ef2 - Ef * Ef) * (Eg2 - Eg * Eg)); } 

Voici la matrice de corrélation de différents crypto-actifs en 2 mois.

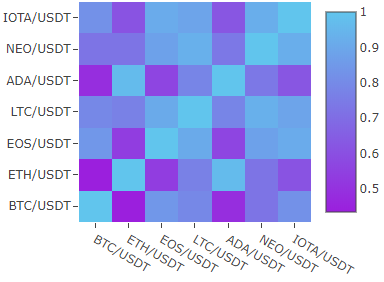
Test d'unité d'indicateur

Si nous avons des tableaux précis de valeurs d'indicateur, nous pouvons tester avec précision notre calcul. Il existe différentes façons de déterminer la mesure d'erreur entre les deux fonctions, mais dans ce cas, l'erreur quadratique moyenne normalisée est mieux adaptée car elle est une quantité sans dimension contrairement à RMSE et elle est relative.

$$

$$\ mathrm {NRMSE} = \ gauche. \ sqrt {\ frac {\ sum (\ hat x_i - x_i) ^ 2} {N}} \ middle / (\ max {x_i} - \ min {x_i}) \ right.$$

Par exemple, le bitcoin peut coûter 20 000 $ et une différence de 10 $ est faible, tandis que lorsque l'altcoin entier peut coûter 1 $ et la différence de 10 $ est énorme.

 function nrmse(f, g) { let sqrDiff = pointwise((a, b) => (a - b) * (a - b), f, g); return Math.sqrt(mean(sqrDiff)) / (Math.max(...f) - Math.min(...f)); } 

Nous pouvons également utiliser MAPE mais ce n'est pas comutatif et avoir un problème proche de zéro.

Conclusion

Voilà. En quelques lignes de code, nous pouvons exprimer les indicateurs techniques de base, si vous aimez cette explonation, consultez ma bibliothèque sur github. Vous y trouverez bien plus. Si vous souhaitez utiliser des algorithmes d'apprentissage automatique pour votre bot, cochez l'indicateur Zig-Zag comme points d'entrée.

Les références

1. StockCharts - une liste d'algorithmes avec des données de test dans les tableaux.
2. Cryptowatch - paramètres d'indicateurs bien réglés.
3. Github - mon code source.

PS Si vous trouvez des erreurs dans le texte, veuillez m'en informer directement.