Connaissance du réseau neuronal le plus simple et de sa mise en œuvre pas à pas

Une fois, je suis tombé sur un livre intitulé "Créez votre réseau neuronal" , écrit par Tarik Rashid . Contrairement à de nombreux autres livres sur les réseaux de neurones, tout a été présenté dans un langage simple, avec un nombre suffisant d'exemples et de conseils

Inspiré par ce livre, je veux le parcourir pas à pas - à savoir sa partie pratique - en écrivant le code d'un réseau neuronal simple .
Cet article s'adresse à ceux qui veulent faire des réseaux de neurones et de l'apprentissage automatique, mais qui ont jusqu'à présent du mal à comprendre ce domaine scientifique étonnant. Le squelette le plus simple du code d'un réseau neuronal sera décrit ci-dessous, afin que beaucoup comprennent le principe le plus simple de construction et d'interaction de tout ce que ce réseau neuronal consiste.




Les théories sur l'apprentissage automatique et les réseaux de neurones sur l'Habré suffisent. Mais si quelqu'un en a besoin, je laisserai quelques liens à la fin de l'article. Et maintenant, nous allons commencer à écrire du code directement, et nous allons écrire en Python , je recommande d'utiliser Jupyter-Notebook lors de l'écriture de code

Étape 1. Initialisation du réseau

Tout d'abord, bien sûr, nous devons initialiser tous les composants actifs de notre réseau

# numpy —    Python,        import numpy #  scipy.special , -scipy    , ,  ,      ,       ,   - " " import scipy.special #,      import matplotlib.pyplot #     class neuralNetwork: #     def __init__(self, inputnodes, hiddennodes, outputnodes, learningrate): #     ,   ,   ,  ) #     ,  ,   self.inodes = inputnodes self.hnodes = hiddennodes self.onodes = outputnodes #    , wih -       ,    who-       self.wih = numpy.random.rand(self.hnodes, self.inodes) self.who = numpy.random.rand(self.onodes, self.hnodes) #   -  ,  ,  ,    ,     ,     ,  ,  ,   self.lr = learningrate #  -   self.activation_function = lambda x: scipy.special.expit(x) 

Sigmoïde

Cette fonction appartient à la classe des fonctions continues, prend un nombre réel arbitraire (c'est-à-dire pas nécessairement un entier) à l'entrée et donne un nombre réel dans la plage de 0 à 1 à la sortie .

En particulier, les grands nombres (modulo) négatifs se transforment en zéro et les grands nombres positifs en deviennent un .

Sa sortie est bien interprétée comme le niveau d'activation des neurones: de l' absence d'activation (0) à l' activation complètement saturée (1).

La sigmoïde est exprimée par la formule:



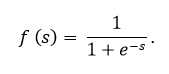
Le graphique de la fonction sigmoïde conformément à la figure ci-dessous:



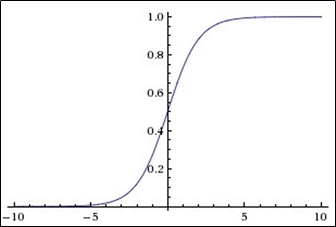
La fonction sigmoïde est:

• continu
• en augmentation monotone;
• différenciable.

Dans ce code, le sigmoïde est présent, comme vous pouvez le voir, sous le nom expit (x)

Un peu sur l'apparence d'un nœud dans un réseau de neurones

L'image montre le plus ce nœud, seulement il est généralement présenté sous la forme d'un cercle, pas d'un rectangle. Comme nous le voyons, à l'intérieur d'un rectangle (enfin, ou d'un cercle) - tout cela est abstrait, il y a 2 fonctions:

La 1ère fonction est engagée dans le fait qu'elle reçoit toutes les entrées, en tenant compte des poids, des données, et parfois même en tenant compte du neurone de déplacement (un neurone spécial qui permet simplement aux graphiques de se déplacer, et non de se mélanger dans un tas laid, c'est tout)

La 2e fonction prend comme paramètre la même valeur que la première fonction additionnée, et cette deuxième fonction est appelée fonction d'activation. Dans notre cas, un sigmoïde

Nous continuons :

Partie 2. Formation au réseau neuronal

 def train(self, inputs_list, targets_list): #       inputs = numpy.array(inputs_list, ndmin=2).T #     input targets = numpy.array(targets_list, ndmin=2).T #  targets #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,       .    ,       hidden_inputs (1 ),        -   (2 ) hidden_outputs = self.activation_function(hidden_inputs) #    ()  final_inputs = numpy.dot(self.who, hidden_outputs) #  ,     final_outputs = self.activation_function(final_inputs) #   ( - ) output_errors = targets - final_outputs #      ,    <b>  </b>,   <b>       </b>(      ) hidden_errors = numpy.dot(self.who.T, output_errors) #        ( ,      ) self.who += self.lr * numpy.dot((output_errors * final_outputs * (1.0 - final_outputs)), numpy.transpose(hidden_outputs)) #       (       ) self.wih += self.lr * numpy.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), numpy.transpose(inputs)) 

Et maintenant nous approchons de la fin

Partie 3. Interrogation d'un réseau de neurones

 #  ,      def query(self, inputs_list): #         inputs = numpy.array(inputs_list, ndmin=2).T #      hidden_inputs = numpy.dot(self.wih, inputs) #  ,     hidden_outputs = self.activation_function(hidden_inputs) #      final_inputs = numpy.dot(self.who, hidden_outputs) #     ,     final_outputs = self.activation_function(final_inputs) return final_outputs 

Nous le menons à terme

 #     ,  ,  (  <b></b>-    , ,   input_nodes = 3 hidden_nodes = 3 output_nodes = 3 #    -   , ... 0.3! learning_rate = 0.3 #   (n    neuralNetwork ,      __init__ ,        n = neuralNetwork(input_nodes,hidden_nodes,output_nodes, learning_rate) 

PS

Ci-dessus a été présenté le modèle le plus simple d'un réseau de neurones. Mais aucune application spécifique n'a été montrée.

Si vous le souhaitez, vous pouvez aller plus loin en ajoutant la possibilité de reconnaître le texte manuscrit dans le code MNIST , pour cela vous pouvez comprendre complètement (et juste vous amuser) avec ce fichier jupyter , ma tâche était de démontrer le code et, si possible, de mâcher sur le réseau et pour quelles réponses

PPS

Vous trouverez ci-dessous des liens utiles:

1. Lien vers Github Tarik ->
2. Son livre ->
3. Théorie de l'apprentissage automatique ->
4. Théorie de l'apprentissage automatique ->
5. Théorie de l'apprentissage automatique ->