Julia et l'essaim de particules

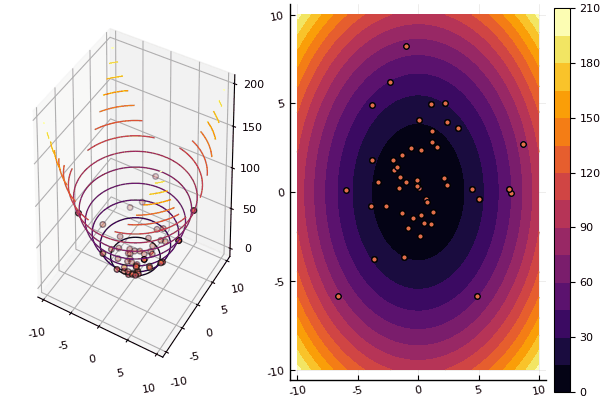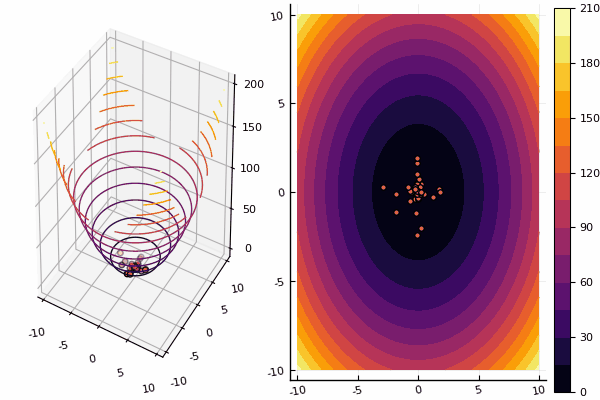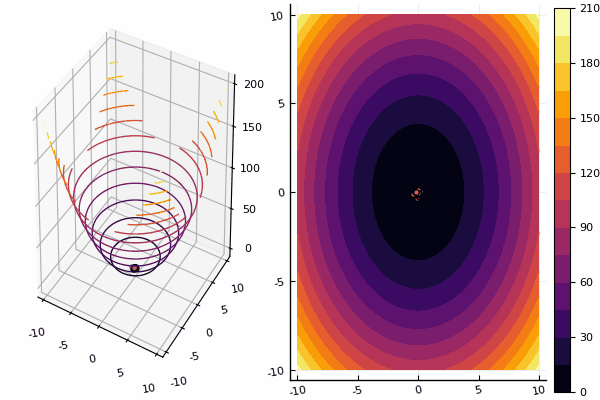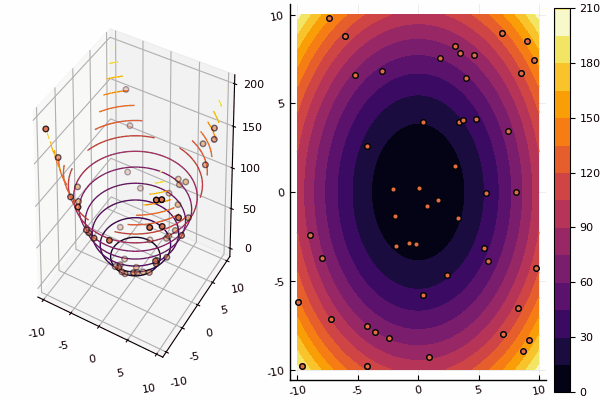
Nous continuons d' étudier les méthodes d'optimisation multidimensionnelle, et la prochaine en ligne est la méthode de l'essaim de particules, qui recherche un minimum global.

Théorie

• Wikipédia
• Diverses méthodes d'essaim de particules et leurs topologies
• Un essaim de particules en Python et C #
• Méthode d'optimisation d'un pack de joints

L'algorithme est assez simple:

La position de chaque particule à un certain moment est calculée par la formule:

O Where $$$p_i$- coordonnées de la meilleure solution pour une particule particulière, $$$g_i$- les coordonnées de la meilleure solution pour toutes les particules de cette époque, $$$C_p$et $$$C_g$- facteurs de pondération (sélectionnés pour un modèle spécifique), $$$A_c$Est le coefficient d'inertie, il peut être rendu dépendant du nombre d'une époque, puis les vitesses des particules changeront en douceur.

Fonctions de test

Puisqu'il est très agréable de regarder le travail de la méthode, nous aurons plus de fonctions de test:

parabol(x) = sum(u->u*u, x) # f(0,0) = 0, x_i ∈ [-10,10] shvefel(x) = sum(u-> -u*sin(sqrt(abs(u))), x) # f(420.9687,420.9687) = -819?, x_i ∈ [-500,500] rastrigin(x) = 10*length(x) + sum(u->u*u-10*cos(2*pi*u), x) # f(0,0) = 0, x_i ∈ [-5,5] ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] bill(x) = (1.5-x[1]+x[1]*x[2])^2 + (2.25-x[1]+x[1]*x[2]*x[2])^2 + (2.625-x[1]+x[1]*x[2]^3)^2 # f(3,0.5) = 0, x_i ∈ [-5,5] boot(x) = (x[1]+2x[2]-7)^2 + (2x[1]+x[2]-5)^2 # f(1,3) = 0, x_i ∈ [-10,10] bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] levy13(x) = sinpi(3x[1])^2 + (1+sinpi(3x[2])^2)*(x[1]-1)^2 + (1+sinpi(2x[2])^2)*(x[2]-1)^2 # f(1,1) = 0, x_i ∈ [-10,10] himmelblau(x) = (x[1]^2+x[2]-11)^2 + (x[1]+x[2]^2-7)^2 # f(3,2)... = 0, x_i ∈ [-5,5] camel3humped(x) = 2x[1]^2 - 1.05x[1]^4 + x[1]^6 /6 + x[1]*x[2] + x[2]^2 # f(0,0) = 0, x_i ∈ [-5,5] izom(x) = -cos(x[1])*cos(x[2])*exp(-( (x[1]-pi)^2 + (x[2]-pi)^2 )) # f(π,π) = -1, x_i ∈ [-100,100] holdertable(x) = -abs(sin(x[1])*cos(x[2])exp(abs( 1-sqrt(x[1]^2+x[2]^2)/pi ))) # f(±8.05502,±9.66459) = -19.2085, x_i ∈ [-10,10] shaffer4(x) = 0.5 + (cos(sin(abs(x[1]^2-x[2]^2)))^2-0.5) / (1+0.001(x[1]^2+x[2]^2))^2 # f(0,1.25313) = 0.292579, x_i ∈ [-100,100] 

Et, en fait, la MRC elle-même:

 function mdpso(; nparts = 50, ndimes = 2, ages = 50, #   lover = [-10 -10], upper = [10 10], C1 = [1.9 1.9], #  - C2 = [1.8 1.8], Ac = [0.1 0.1], ) minind = 0 V = zeros(nparts,ndimes) #   n  n X = zeros(nparts,ndimes) funmin = -Inf Fmin = Inf Fbest = fill(Fmin, nparts) funx = zeros(nparts) xmem = zeros(nparts,ndimes) xbest = zeros(ndimes) #   #      for i in 1:nparts, j in 1:ndimes X[i,j] = randomer(lover[j], upper[j]) end for i in 1:ages for j in 1:nparts funx[j] = fun(X[j,:]) if funx[j] < Fbest[j] Fbest[j] = funx[j] xmem[j,:] = X[j,:] end end #      ploter(lover, upper, X, funx, i); funmin = minimum(funx) minind = argmin(funx) if funmin < Fmin Fmin = funmin xbest[:] = X[minind,:] end for j in 1:nparts, k in 1:ndimes R1 = rand() R2 = rand() V[j,k] = Ac[k]*V[j,k] + C1[k]*R1*(xmem[j,k] - X[j,k]) + C2[k]*R2*(xbest[k] - X[j,k]) X[j,k] += V[j,k] end println("Age № $i\n xbest:\n $(xbest[1]) $(xbest[2])") println("Fmin: $Fmin\n") end f = open("$fun.txt","w") #      write(f,"C1 = $C1, C2 = $C2, Ac = $Ac, lower = $lover, upper = $upper, ages = $ages, parts = $nparts") close(f) end 

Avec les dessins, cependant, le calcul prend plus de temps, mais il est plus joli:

 using Plots pyplot() function ploter(l, u, xy, z, n_age ) contour(Xs, Ys, Zs, fill = true); #    (   ) #   ,       scatter!(xy[:,1], xy[:,2], legend = false, xaxis=( (l[1], u[1])), yaxis=( (l[2], u[2])) ); #savefig("$fun $n_age.png") #        end fun = bill low = [-4 -4] up = [4 4] Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] surface(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) 

 mdpso(C1 = [1.2 1.2], C2 = [1.1 1.1], Ac = [0.08 0.08], lower = [-4 -4], upper = [4 4], ages = 30) 

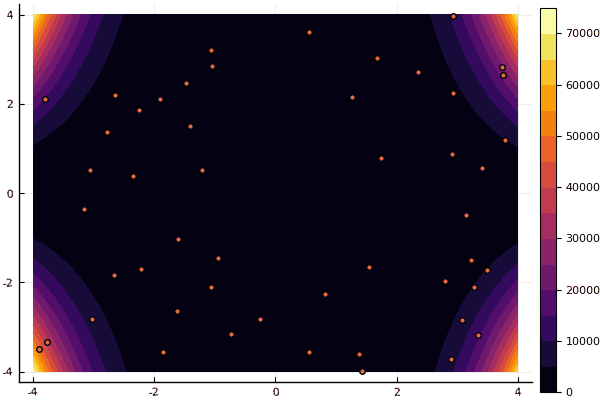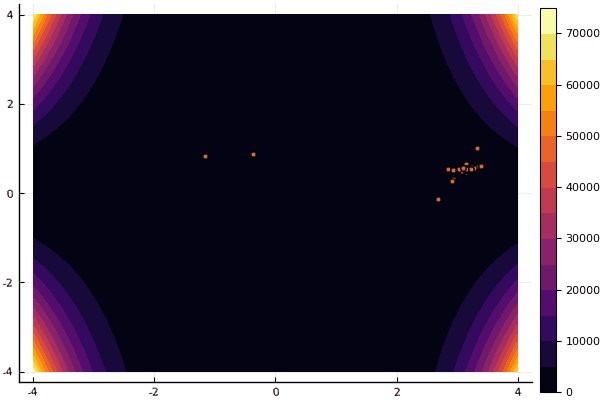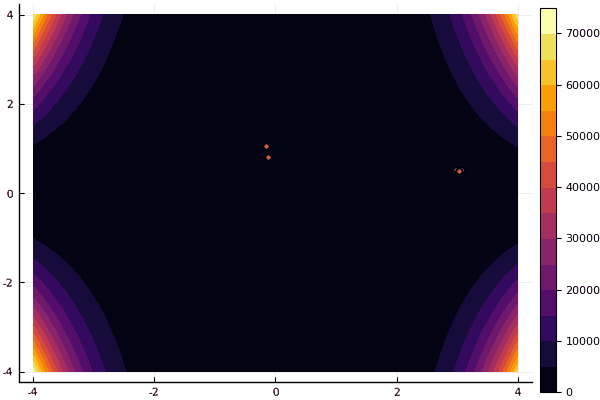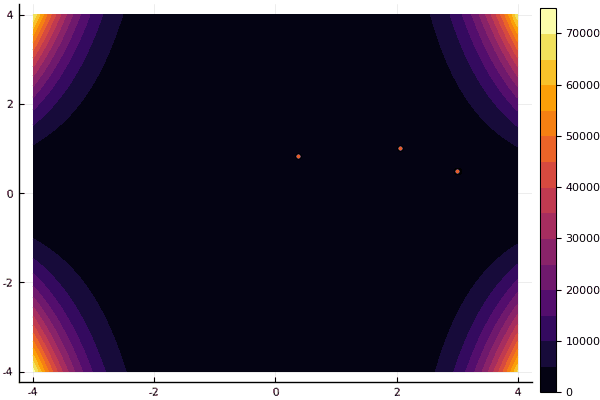
 fun = ekly mdpso(C1 = [1.7 1.7], C2 = [1.7 1.7], Ac = [0.07 0.07], lower = [-5 -5], upper = [5 5], ages = 15) 

 fun = himmelblau mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-5 -5], upper = [5 5], ages = 20, parts = 50) 

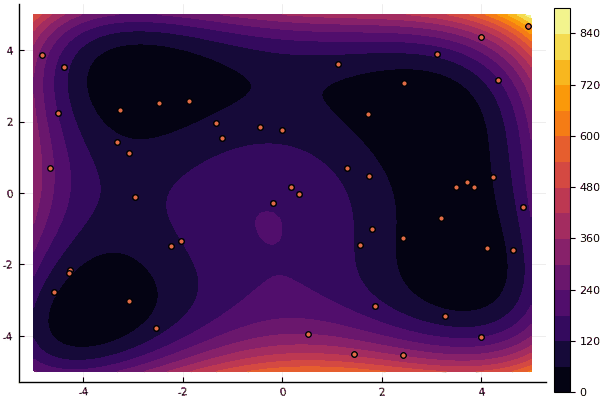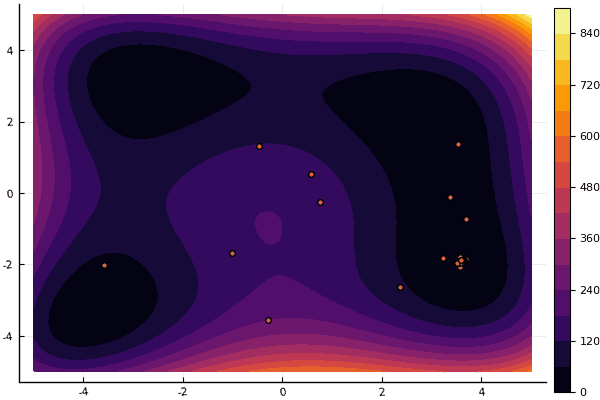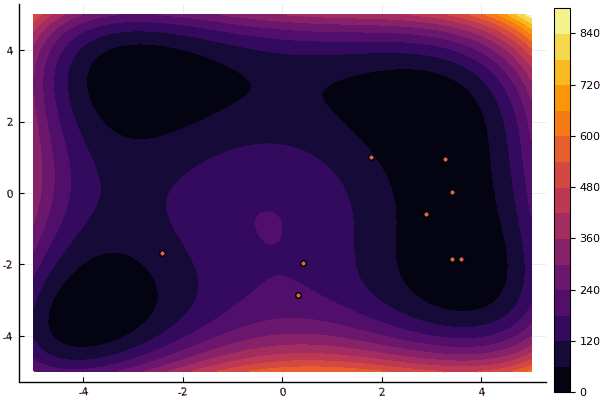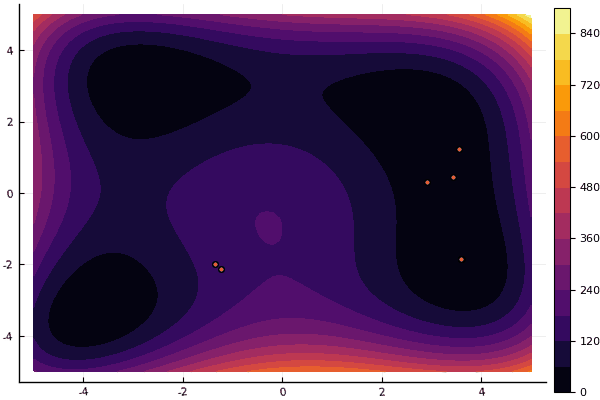
 fun = holdertable mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

 fun = levy13 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

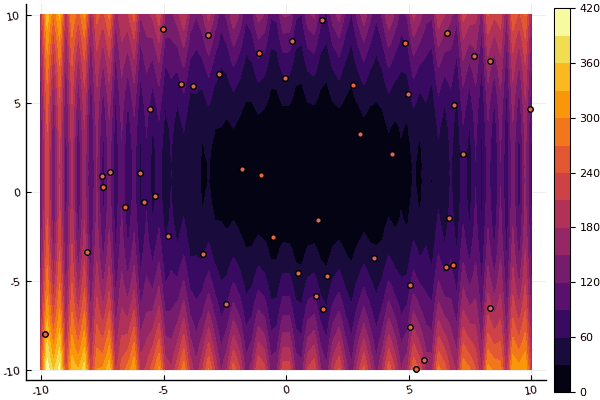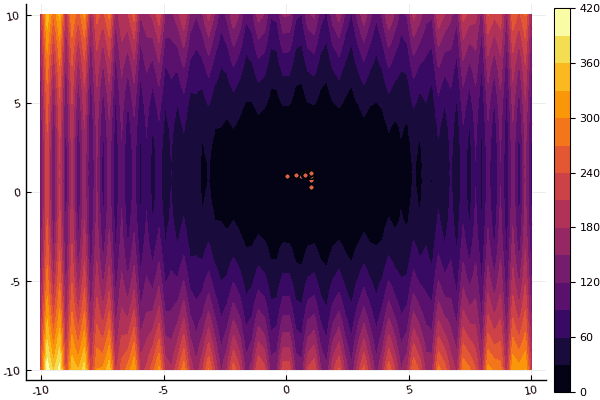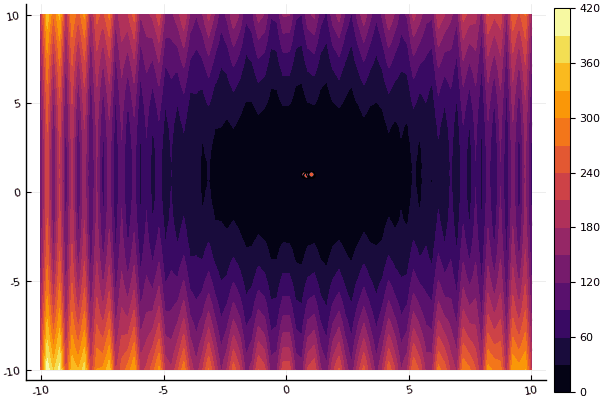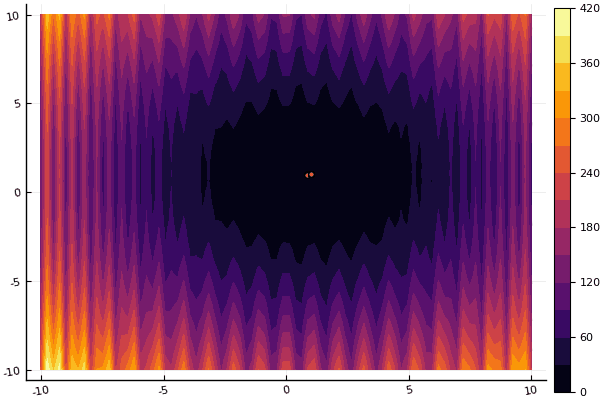
 fun = shaffer4 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-100 -100], upper = [100 100], ages = 20, parts = 50) 

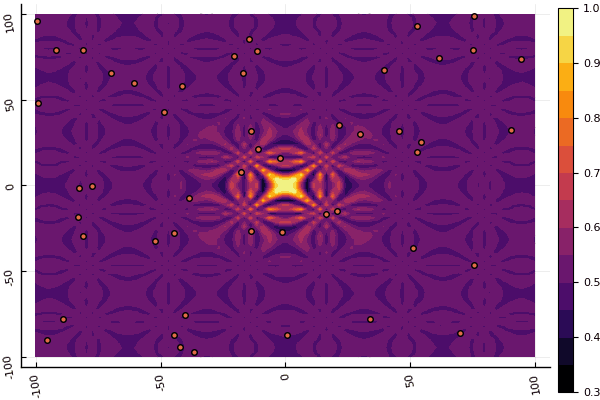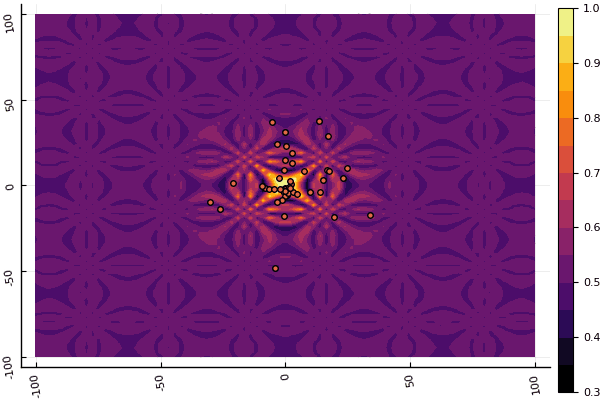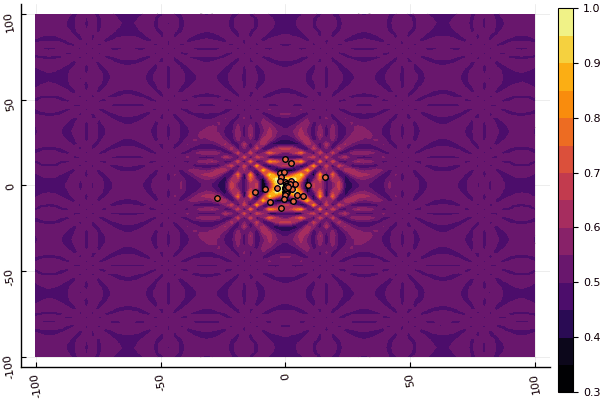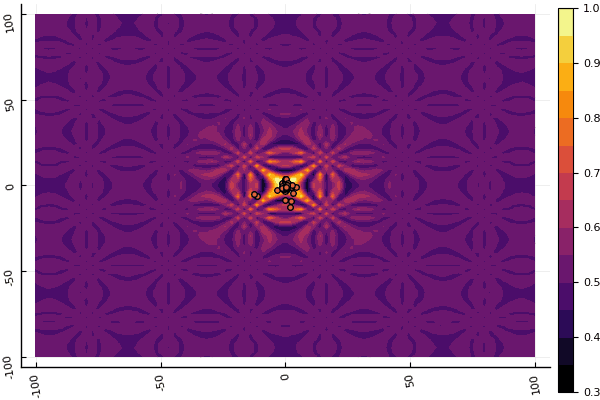
Ce qui déprime vraiment, ce sont les paramètres et un élément aléatoire: si une particule ne vole pas près du minimum global, alors tout cela peut tomber en local:

 fun = rastrigin mdpso(mdpso(C1 = [0.1 0.1], C2 = [1 1], Ac = [0.08 0.08], lover = low, upper = up, ages = 30)) 

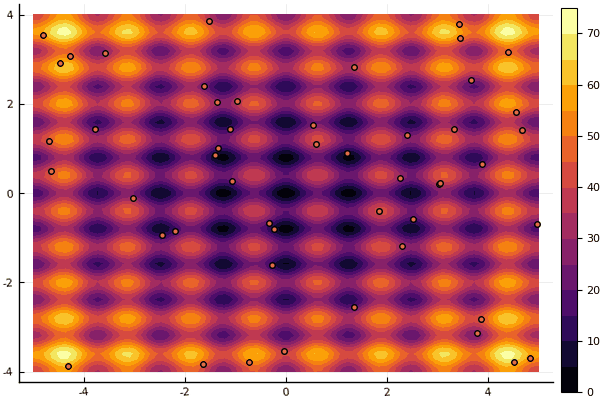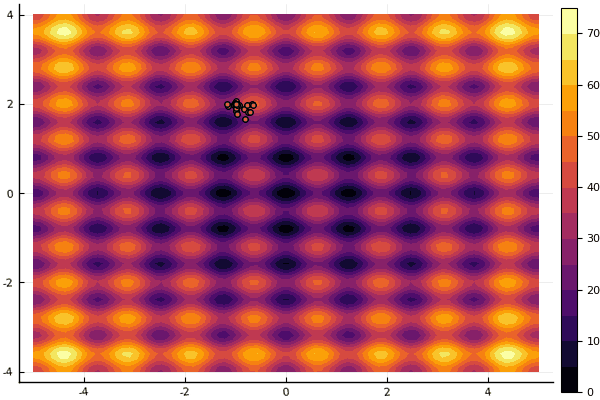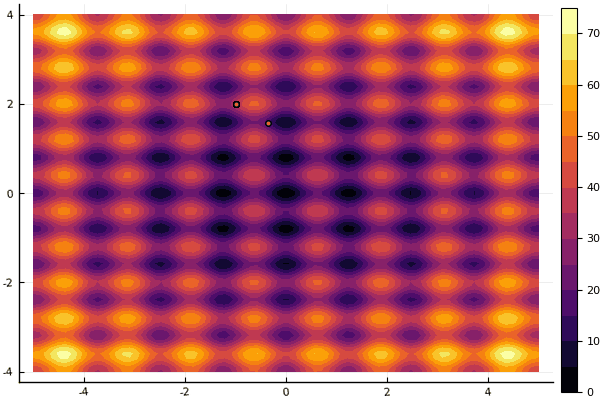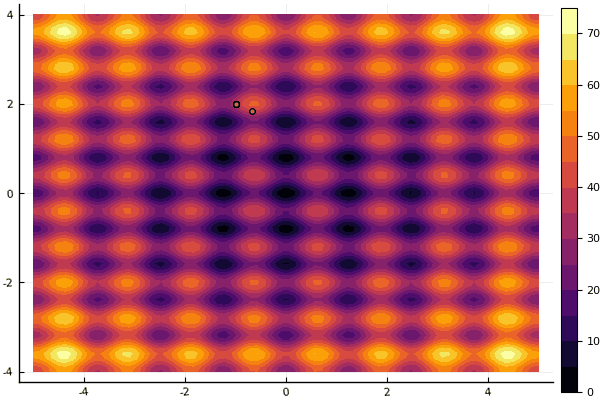
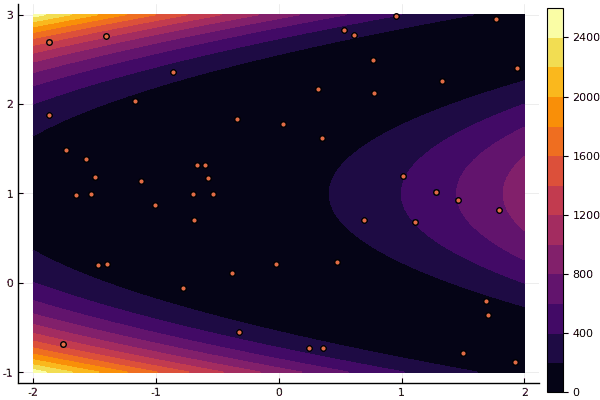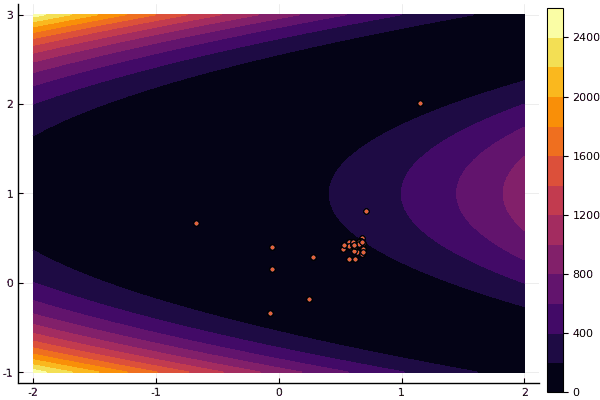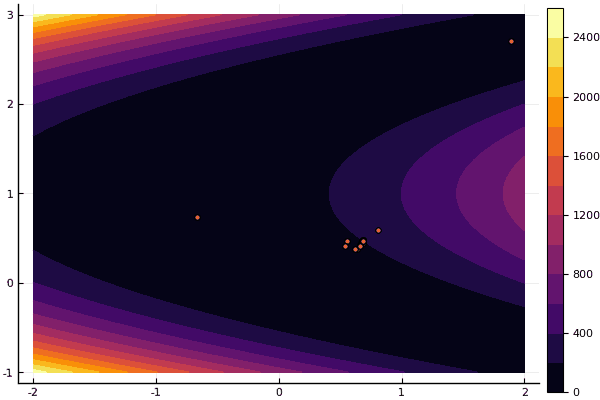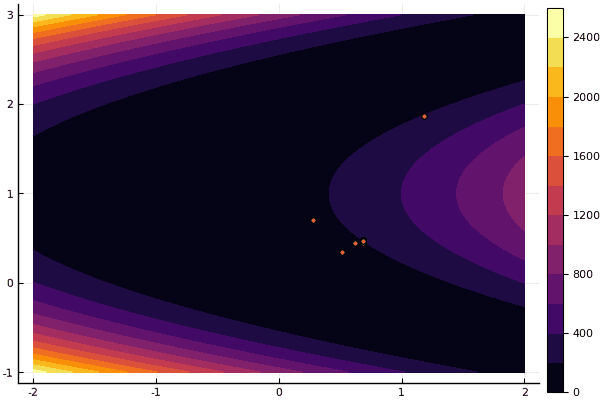
Oui et vieux pas très bon Rosenbrock ne permet toujours pas de se comprendre:

 fun = rosenbrok mdpso(C1 = [1.7 1.7], C2 = [1.5 1.5], Ac = [0.15 0.15], lover = low, upper = up, ages = 20, nparts = 50) ... Age № 20 xbest: 0.37796421341886866 0.12799160066705667 Fmin: 0.409026370833564 

Mais comme je l'ai dit plus tôt, vous pouvez utiliser le FDM pour rechercher une bonne approximation du minimum global, puis spécifier, par exemple, Nelder-Mead:

 vecl(x) = sqrt( sum(u -> u*u, x) ) function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] end function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) k = 0 N = ndimes Xx = zeros(N, N+1) for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end println(k, " ", p, " ", Xx[:,1]) p = normx(Xx) end #while fit = Xx[:,1] end 

 ofNelderMid(fit = [0.37796 0.127992]) ... 92 0.00022610400555036366 [1.0, 1.0] 93 0.00015987967588703512 [1.0, 1.0] 94 0.00011305200343052599 [1.0, 1.0] 2-element Array{Float64,1}: 0.9999999996645973 0.9999999995466575 

Pour le MFC classique, tout n'est pas clair avec le critère d'arrêt: le meilleur point peut tenir la position de plusieurs époques, les distances entre certaines particules ne peuvent pas non plus changer longtemps. Par conséquent, une limite sur le nombre d'époques est utilisée. Pour augmenter les chances de trouver un minimum global, il faut augmenter le nombre de particules et d'époques, ce qui est très coûteux en mémoire et, en plus, en temps (pas de blague, 50 appels de la fonction objectif pour chaque dimension à chaque itération).

Moral

• Si vous ne voulez pas ou ne pouvez pas utiliser des méthodes complexes et modernes, vous pouvez utiliser des compositions de méthodes plus simples
• Très souvent, pour un problème, il existe une méthode étroitement affûtée (par exemple, pour les fonctions de ravin)
• Il est conseillé d'avoir plusieurs OM différents sous la main pour une comparaison cohérente
• Il n'est pas toujours possible de mettre votre tâche dans la méthode et d'obtenir la bonne réponse tout de suite - vous devriez passer du temps à rechercher, à varier les paramètres, si vous ne pouvez pas voir le relief, vous devez au moins imprimer les calculs intermédiaires afin de suivre la convergence.

C'est tout pour aujourd'hui, merci de votre attention et je vous souhaite à tous une bonne optimisation!