Les preuves / arguments à connaissance zéro sont une technologie cryptographique émergente qui promet de nous rapprocher du Saint Graal de la blockchain: la confidentialité et l'auditabilité des données.
Les applications potentielles pour la connaissance zéro incluent, mais ne sont pas limitées à:
Une autre application pour les preuves à connaissance zéro aide à faire évoluer les chaînes de blocs. Les ZKP permettent la «compression» des calculs pour les transactions blockchain sans sacrifier la sécurité.
Dans cet article, nous décrivons comment la connaissance zéro (en particulier, Bulletproofs ) peut être appliquée pour créer un service axé sur la confidentialité à l'aide de la plate-forme Exonum de Bitfury.
Analyse situationnelle
Il est possible d'atteindre un
certain niveau de confidentialité des données dans les applications blockchain en utilisant l'approche du «jardin clos», où les données sont cachées car l'accès y est restreint à l'aide de pare-feu, d'un contrôle d'accès basé sur les rôles, de
douves et d'autres mesures de sécurité du périmètre . Les données sensibles dans la blockchain peuvent être cryptées (peut-être, avec un schéma de cryptage à clé publique, avec les clés publiques pertinentes gérées par la même blockchain) et / ou stockées en dehors de la blockchain (dans ce cas, la blockchain stocke uniquement les empreintes digitales de hachage de les données). Cette approche est utilisée dans de nombreux cadres de registres distribués autorisés.
Cependant, les inconvénients de l'approche du «jardin clos» deviennent de plus en plus évidents. Pour le dire franchement, l'approche est contraire à l'un des principaux arguments de vente de la blockchain - l'auditabilité. Si les données sur la blockchain ne peuvent pas être auditées en consultant la logique du contrat intelligent, la blockchain devient un service d'
horodatage lié glorifié. Le fait qu'il y ait des données sur la blockchain ne signifie plus que ces données sont valides selon les règles du contrat intelligent. Le deuxième inconvénient majeur de l'approche du jardin clos est qu'elle n'est pas évolutive. Le directeur technique de R3, Richard Brown, par exemple, a bien
comparé le modèle de confidentialité de leur solution aux canaux Slack - il est difficile d'ajouter ou de retirer des participants du jardin en toute sécurité, d'autant plus lorsqu'il n'y a aucune attente préalable quant au nombre et à l'identité de ces derniers. participants.
C'est là que la
connaissance zéro peut être précieuse. De par leur conception, les preuves et arguments à connaissance zéro prouvent de manière convaincante une déclaration sur les données privées sans rien révéler des données, à l'exception de la déclaration prouvée. Il est facile de rendre les preuves de connaissance zéro
universellement vérifiables, sans sacrifier la vie privée! ² Cette fonctionnalité est exactement ce qui est nécessaire pour construire un système à la fois respectueux de la vie privée et vérifiable.
Notre recherche
Pour démontrer l'utilisation de preuves à connaissance nulle, nous allons créer un service de crypto-monnaie avec des fonctionnalités similaires aux services de didacticiel de la
documentation Exonum . Le service permet d'enregistrer les utilisateurs et les portefeuilles (en fournissant un solde de jetons initial en récompense) et de transférer des jetons entre les partis enregistrés. Toutes les transactions sont authentifiées à l'aide d'un cryptosystème de signature numérique, Ed25519, intégré aux services Exonum. Nous ne cachons pas l'identité des parties à la transaction (c'est-à-dire leurs clés publiques), mais nous masquons le nombre de jetons traités et le solde de chaque compte dans le système. Nous discutons également de la façon dont nous pourrions améliorer le service pour masquer les entités de transaction à la fin de l'article.
Le service est entièrement open source et peut être consulté
ici .
Fond de cryptographie
Afin de comprendre le fonctionnement du service, nous devons d'abord nous présenter au cœur de la primitive cryptographique qui sous-tend les Bulletproofs - un concept appelé
engagements Pedersen . Un schéma d'engagement cryptographique est un peu comme une fonction de hachage: quelqu'un entre des données secrètes (l'ouverture) et obtient la sortie qui est brouillée de manière méconnaissable (l'engagement). On peut alors révéler l'ouverture pour prouver que la valeur engagée y correspond.
La différence avec les fonctions de hachage est qu'en plus d'être
contraignant (personne ne peut concevoir deux ouvertures différentes produisant le même engagement), un schéma d'engagement devrait également se
cacher (il est impossible d'inverser le schéma et de produire une ouverture avec un engagement). Une fonction de hachage se cache si son entrée est répartie uniformément sur tout l'espace d'entrée, mais cette hypothèse ne s'applique pas le plus souvent aux engagements (en effet, il doit être possible de valider une valeur à partir d'un très petit ensemble, tel que booléen). En tant que telle, l'ouverture contient, outre la charge utile, le
facteur aveuglant qui rend (au moins statistiquement) improbable de deviner la charge utile compte tenu de l'engagement.
Le schéma d'engagement de Pedersen utilise un
groupe d'ordre premier , dans lequel le
problème du logarithme discret (DLP) est considéré comme difficile, avec deux générateurs,
G et
H. G et
H doivent être choisis de telle manière que la relation logarithmique discrète entre eux soit inconnue; en d'autres termes, personne ne connaît
k tel que
H = kG .³ L'ouverture est une paire
(x, r) , où
x est la valeur engagée et
r est le facteur aveuglant; les deux sont des scalaires de groupe (essentiellement, des entiers avec «débordement» semblables aux types d'entiers finis utilisés dans la plupart des langages de programmation). L'engagement est calculé comme
Comm (x; r) = xG + rH . Il peut être prouvé que si DLP dans le groupe est difficile, l'engagement Pedersen est contraignant sur le plan informatique et se cache parfaitement.
La propriété cruciale des engagements Pedersen est qu'ils sont additifs: la somme (ou la différence) de 2 engagements est un engagement à la somme (ou différence) des valeurs engagées. En effet,
C1 = x1 G + r1 H; C2 = x2 G + r2 H => C1 + C2 = (x1 + x2) G + (r1 + r2) H = Comm(x1 + x2; r1 + r2).
Nous n'incluons pas les détails ici sur la façon dont les pare-balles sont construits et vérifiés, mais plus d'informations peuvent être trouvées dans les ressources suivantes - [
1 ] et [
2 ]. Il suffit de noter que la borne supérieure
M est supposée avoir la forme
2 ^ (2 ^ n) , ce qui conduit à la construction de preuve la plus efficace.
Construire un service
Grâce à nos connaissances, nous pouvons masquer en toute sécurité les soldes des comptes et les montants de transfert à l'aide des engagements de Pedersen. En utilisant des preuves de portée, nous pouvons prouver / vérifier qu'un transfert est correct:
- Le montant transféré est positif
- L'expéditeur dispose d'un solde suffisant sur son compte.
Pour la première preuve, nous prenons l'engagement sur le montant du transfert,
C_a (il est directement présent dans la transaction de transfert), et vérifions que la valeur engagée dans
C_a-Comm (1; 0) se situe dans la plage
[0, M) . En effet, cela revient à prouver que
C_a correspond à une valeur dans la plage
[1, M] . L'expéditeur peut produire cette preuve, car il connaît le montant transféré
a .
Pour la deuxième preuve, nous devons prendre l'engagement pour le solde actuel de l'expéditeur,
C_s , et vérifier que la valeur engagée dans
C_s-C_a se situe dans la plage
[0, M) . Encore une fois, l'expéditeur peut produire cette preuve car il connaît l'ouverture aux deux
C_s et
C_a .
Pour appliquer le transfert à l'état blockchain, nous soustrayons l'engagement de montant
C_a de l'engagement de
solde de l'expéditeur (comme nous l'avons vérifié, il ne peut pas conduire à un solde négatif ou à l'augmentation du solde de l'expéditeur), puis ajouter
C_a à celui du destinataire. engagement d'équilibre.
Détails clés
Il est important de noter que quelques conditions peuvent rendre le service implémenté plus complexe.
Le destinataire d'un transfert doit trouver l'ouverture à
C_a quelque part; sinon, il ne connaît plus l'ouverture de son équilibre et ne peut plus rien faire avec son portefeuille. L'ouverture n'est pas présente dans le texte en clair de la transaction de transfert (qui est le point entier). Nous
pourrions supposer que le récepteur obtient de manière fiable l'ouverture via un canal hors chaîne (par exemple, envoyé par l'expéditeur via Telegram), mais ce n'est pas un scénario illustratif. Donc, à la place, nous chiffrons l'ouverture en utilisant un chiffrement à clé publique à deux parties basé sur l'échange de clés Diffie-Hellman (libsodium appelle ce type de
boîte de chiffrement). Pour l'avantage supplémentaire, les clés Curve25519 requises pour la routine de
boîte peuvent être converties à partir des clés Ed25519, nous pouvons donc continuer à utiliser une seule paire de clés pour chaque utilisateur au lieu d'introduire des clés de chiffrement distinctes.

Une fois que nous avons introduit le cryptage, nous ne pouvons plus appliquer le transfert de manière atomique. En effet, l'expéditeur peut fournir de manière malveillante ou involontaire des ordures au lieu du cryptage d'ouverture, et la logique de la chaîne de blocs ne pourra pas dire que c'est le cas.⁶ Ainsi, nous demandons au destinataire d'accepter explicitement le transfert via une transaction distincte.
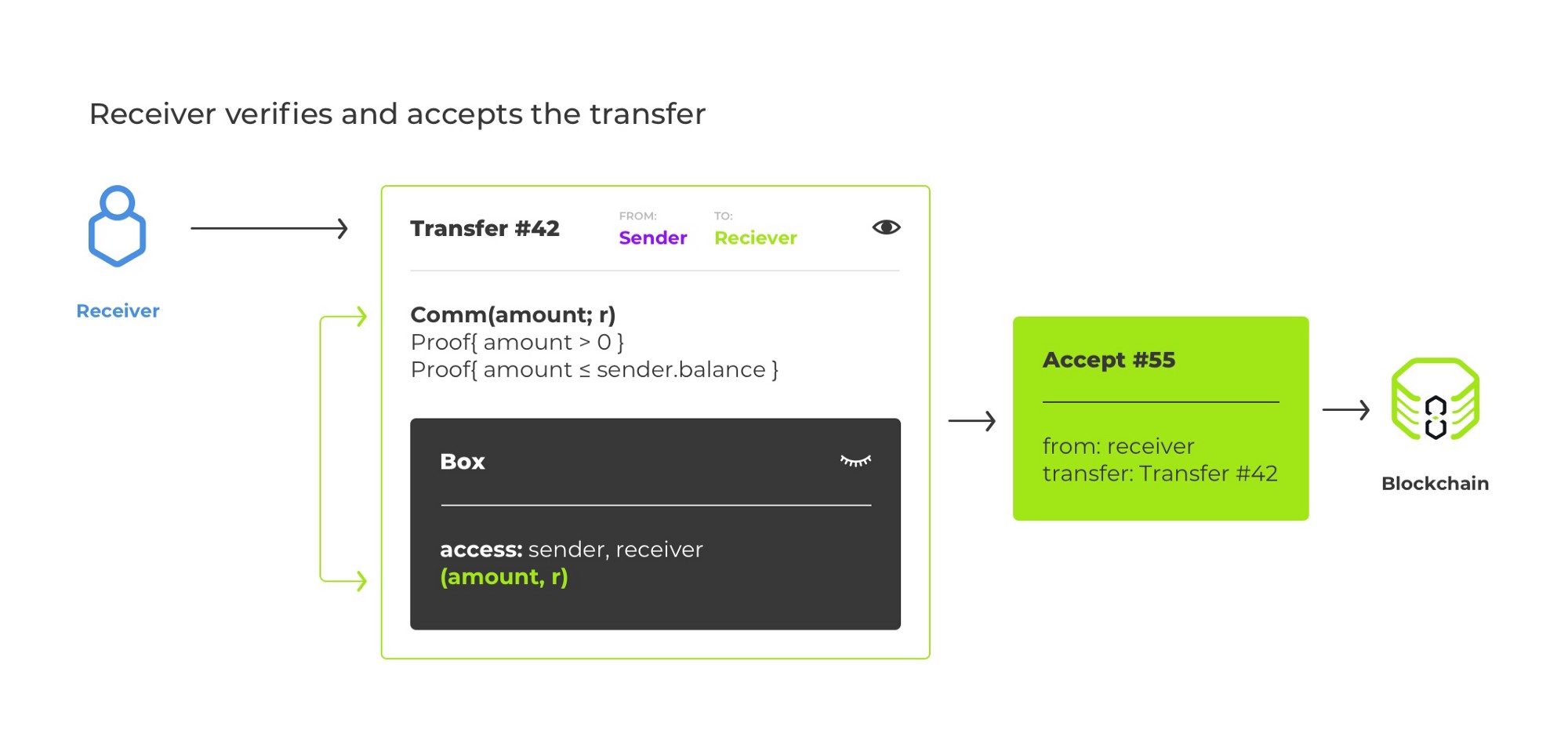
Avant qu'un virement ne soit accepté, il modifie l'engagement de solde de l'expéditeur (sinon, nous autoriserions une double dépense!), Mais pas celui du destinataire.

Une fois la transaction d'acceptation confirmée par le réseau blockchain, le solde du récepteur est mis à jour et le transfert est terminé.

Pour éviter les interblocages, un transfert spécifie un délai de verrouillage temporel (en hauteur relative de la blockchain,
CSV du Bitcoin) pour que le récepteur signale l'acceptation. Si le verrouillage de l'heure est expiré, le transfert est automatiquement remboursé à l'expéditeur (Exonum le permet via le crochet
Service :: beforeCommit () ).
Un autre problème est plus complexe. Pour produire la preuve d'un solde suffisant, l'expéditeur doit connaître son solde actuel, ce qui n'est pas toujours le cas. Une transaction d'acceptation ou un remboursement erroné peut augmenter le solde de l'expéditeur à son insu; dans ce cas, le transfert échouera à la vérification et l'expéditeur sera raisonnablement frustré.
Pour atténuer ce problème, nous permettons aux transferts de référencer ce que l'expéditeur pense être son état de portefeuille actuel (plus précisément, la référence prend la forme du nombre d'événements qui changent le solde du compte - transferts et remboursements). Lors de la vérification de la preuve d'un solde suffisant, nous utilisons l'état référencé pour obtenir l'engagement de solde de l'expéditeur. De plus, nous vérifions qu'aucun transfert sortant ne s'est produit depuis l'état référencé. Si tel est le cas, nous pouvons être certains que si nous soustrayons le montant du transfert du solde
actuel de l'expéditeur, nous aboutirons à une valeur non négative. En effet, les événements de l'historique du compte après le point de référence (virements entrants et remboursements) ne peuvent qu'augmenter le solde! ⁷
Avec des points de référence en place, l'expéditeur est encore quelque peu contraint; il / elle ne doit avoir aucun transfert en attente lors de la création d'un nouveau transfert. Pourtant, cette restriction est beaucoup moins limitative que l'exigence de connaître l'état de son compte au moment du virement; fondamentalement, nous faisons dépendre l'expéditeur de ce
qu'il a fait auparavant, mais pas des actions des autres.
Implémentation
Nous utilisons une bibliothèque pare-balles écrite en
rouille pure, qui a récemment atteint le stade de la
pré-version . Comme la plateforme Exonum est écrite en Rust, elle s'intègre parfaitement à la bibliothèque. En prime, contrairement à la version des pare-balles décrite dans le livre blanc original (qui est développé en
C et utilise la courbe elliptique secp256k1 de Bitcoin), la bibliothèque que nous utilisons est basée sur Curve25519, qui est déjà utilisé dans Exonum comme composant principal du Cryptosystème à signature numérique ED25519.
La mise en œuvre du service sur la base de la description ci-dessus est assez simple. La partie la plus difficile a été de construire des preuves Merkle qui authentifient les informations retournées à l'utilisateur afin qu'il / elle n'ait pas à faire aveuglément confiance aux nœuds Exonum avec lesquels il communique. L'amélioration de l'expérience des développeurs de services à cet égard est l'un des principaux objectifs de la version
Exonum 1.0 .
Prochaines étapes
Le service que nous avons construit ne cache pas l'identité de l'expéditeur et du destinataire des transferts, ce qui constitue une limitation majeure pour les applications du monde réel. Heureusement, il existe des moyens de résoudre ce problème.
La technique générique utilisée dans
zCash (mais principalement applicable à d'autres cas d'utilisation, comme
Ethereum ) est basée sur la création d'un
arbre Merkle de l'état du système. Par exemple, zCash crée l'
arborescence d'engagement de note , qui est à peu près équivalente aux sorties de transaction jamais créées dans Bitcoin. Les preuves de connaissance zéro englobent ensuite les chemins d'authentification (alias branches de Merkle) dans cet arbre, révèlent quelque chose sur un élément de l'arbre sans révéler à quel élément il est fait référence. L'inconvénient de cette approche est que les fonctions de hachage cryptographiques utilisées pour créer des arbres Merkle sont difficiles à transférer dans le domaine de la connaissance zéro; les preuves résultantes deviennent coûteuses en termes de calcul - une seule preuve peut prendre des secondes, voire des minutes à créer. La recherche de fonctions de hachage cryptographiques plus «compatibles avec ZKP» est le domaine de la recherche active.
Si nous admettons des contraintes supplémentaires, il peut y avoir une solution plus simple. Par exemple, un article récent de
Narula et al . décrit un système avec un nombre limité, a priori connu de participants, qui peut effectuer des transactions entre eux sans révéler les participants ou les montants transférés pour toute transaction. (Pensez à un réseau de blockchain axé sur la confidentialité pour les virements interbancaires.)
Sur une note plus prosaïque, il existe probablement de nombreuses améliorations techniques dont le service développé peut bénéficier: plus de couverture de test, séparation des clés de signature et de cryptage, analyse comparative, etc. Une amélioration majeure du service UX serait de permettre un ordre déterministe des transactions provenant du même utilisateur, que nous prévoyons de résoudre peu de temps après la sortie d'Exonum 1.0.
Conclusion
Nous avons décrit comment construire un cryptotoken basé sur un compte avec une confidentialité élevée activée par des preuves à connaissance zéro (en particulier, des pare-balles). La logique de jeton a été implémentée en tant que service Exonum. Bien qu'actuellement, le service ne soit qu'une preuve de concept, il montre comment la plate-forme Exonum peut être utilisée pour créer au-dessus de primitives cryptographiques complexes avec une surcharge très faible imposée par l'environnement d'exécution.
- Il existe une distinction complexe entre les preuves et les arguments, que nous n'entrerons pas ici. Dans un souci de simplicité, nous ferons référence à toutes les constructions à connaissance zéro dans cet article comme des preuves à connaissance nulle même si cela n'est pas toujours correct du point de vue théorique.
- Cela peut être accompli via une technique très générale connue sous le nom de transformation Fiat - Shamir , qui convertit un protocole de preuve interactif en un protocole non interactif et universellement vérifiable. Sacrifiant une fois de plus la rigueur scientifique, nous ne préciserons pas explicitement que les preuves de connaissance zéro que nous utilisons ne sont pas interactives.
- Les générateurs sont généralement choisis avec une méthode «rien dans ma manche». Par exemple, G peut faire partie de la spécification de groupe pour son utilisation dans la cryptographie à clé publique, et H est dérivé de G via une fonction de hachage: H ~ hachage (G) .
- Ce dernier signifie que même un adversaire avec une puissance de calcul infinie ne peut pas déduire ce à quoi l'engagement s'engage; en effet, si le DLP du groupe est rompu, chaque engagement peut être ouvert à toute valeur possible.
- Il s'agit en partie d'une décision de validation de principe; en général, réutiliser des clés à des fins différentes est une mauvaise idée.
- Il est théoriquement possible de fournir une preuve de connaissance nulle pour que la valeur chiffrée soit équivalente au solde engagé; cependant, cela augmenterait considérablement la complexité du système.
- Il convient de mentionner que certains transferts enfreignant la règle «pas de transferts sortants depuis l'état référencé» peuvent toujours être corrects; nous n'avons tout simplement aucun moyen de vérifier cela.