Si vous n'avez pas lu mon premier article sur le sujet, je vous conseille de commencer par
celui-ci .
Comme j'ai mentionné une certaine attitude, quoique très indirecte, envers les mathématiciens financiers, permettez-moi de développer le sujet au point d'absurdité en fonction de la façon dont il est développé dans Risk Analytics. Lors du calcul du prix d'une option, ils tiennent souvent compte de la sensibilité de ce prix à un ensemble de paramètres. Par exemple, comment le prix de l'option changera lorsque le prix de l'action pour laquelle l'option est émise change, ou lorsque la volatilité du prix de l'action, ou le taux de la Banque centrale change, etc.
Nous pouvons être intéressés par la façon dont la probabilité de gagner un jeu change lorsque la probabilité de gagner un point change. En fait, nous voulons calculer la dérivée de la première à la seconde. L'approche la plus simple consiste à l'évaluer à l'œil nu à partir du graphique. On peut voir que le maximum est atteint dans une situation de 50:50. Si les chances de gagner un point passent de 0,45 à 0,55, la probabilité de gagner au badminton passe de 0,26 à 0,74, soit 0,48. Une estimation approximative donne un dérivé de l'ordre de 5. Autrement dit, si vous atteignez 0,51 (soit 51%) avec des chances égales, l'augmentation de la probabilité de gagner le jeu sera d'environ 0,05 (ou 5%). De même, vous pouvez calculer la dérivée à tout autre point du graphique.
En finance, l'approche «bump and run» est généralement utilisée, c'est-à-dire qu'ils modifient légèrement le paramètre et calculent le nouveau prix de l'option et le dérivé. Ayant agi de manière similaire, je cite les données exactes sur le graphique (j'ai pris le changement d'un pourcentage, légèrement grossier, mais acceptable dans cette situation). Pour plus de clarté, il a ajouté des matchs jusqu'à 5 et 31 points. Soit dit en passant, le tir au biathlon peut être considéré comme une fête jusqu'à 5. Ce n'est pas une analogie absolue, car le nombre total de tirs est fixe. Mais les méthodes de solution sont presque les mêmes.
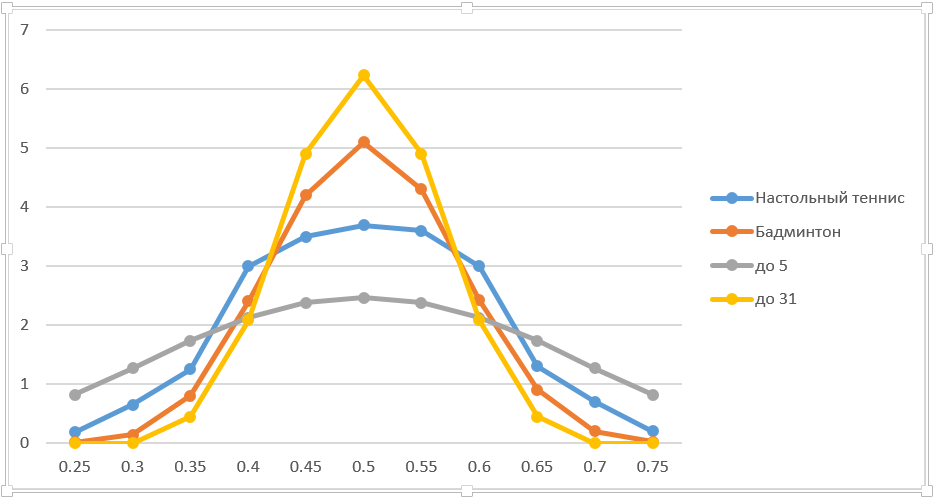
De toute évidence, plus le lot est long, plus le dérivé est élevé à 50:50. Si la durée de la fête tend vers l'infini, la victoire d'un joueur avec même un avantage minime est pratiquement garantie. La largeur de la courbe diminue en conséquence. En général, les conclusions sont assez évidentes.
Vous pouvez calculer la sensibilité à la décharge accidentelle d'un point. Par exemple, alimentez le filet. Dans quelle mesure un glissement affecte-t-il le résultat du jeu? En fait, il s'agit d'une réduction du score gagnant de l'adversaire d'un point. Le graphique ci-dessous reflète cette situation. Naturellement, au tennis de table, il est plus important de perdre un point qu'au badminton. À forces égales, la probabilité de l'issue du jeu diminue autant que possible - de 0,5 à 0,41. Faites attention à l'asymétrie des courbes (contrairement à la plupart des autres). Ce n'est pas un hasard. Le fait est que l’équilibre passe de 50:50 à une probabilité plus élevée de gagner un point, car un point perdu aggrave les chances d’un joueur.
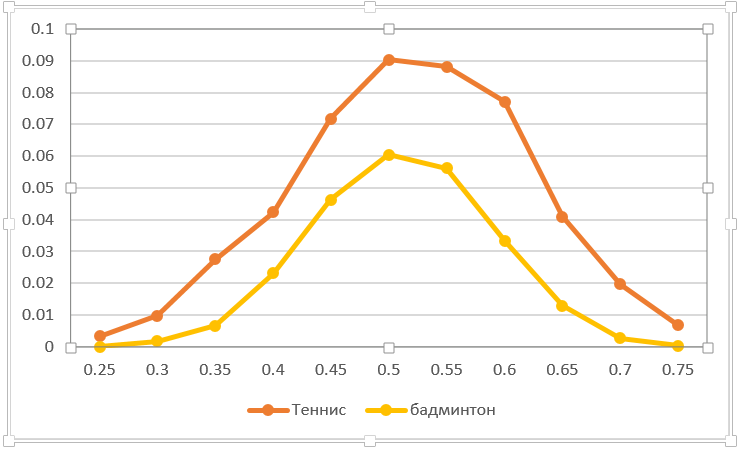
Mettons une autre expérience intéressante. Imaginez que l'un des joueurs puisse se concentrer et jouer 3 points au-dessus de la moyenne (p1 + delta). Supposons qu'après cela, l'alignement revienne à l'original (à la moyenne attendue sans tenir compte de la "poussée de force"). Il est clair que la probabilité de gagner augmentera. La question est: est-ce important de se concentrer - au début ou à la fin du jeu? Je propose de faire une hypothèse avant de poursuivre la lecture.
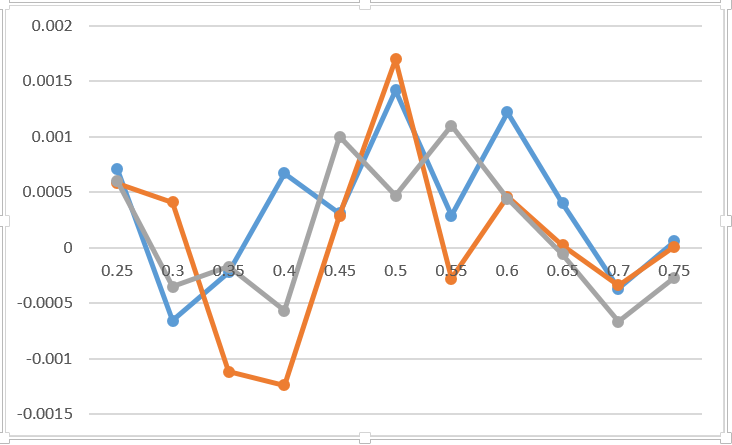
Ainsi, comme le montre l'expérience, il n'y a absolument aucune différence quand exactement se concentrer (les facteurs du plan moral ne sont pas pris en compte). Le graphique montre la différence entre la probabilité de gagner la partie en cas de concentration à 3 endroits différents de la partie par rapport à la concentration sur les 3 premiers points. Je pense que ce graphique reflète l'erreur de Monte Carlo et rien de plus. J'ai ajouté 0,2 au résultat du match nul pour le premier joueur pour trois matchs nuls. Je n’indique même pas sur le graphique quelle ligne correspond à quelle option. Cela ne change absolument rien. Le seul conseil précieux à ce sujet est de se préparer avant qu'il ne soit trop tard.
Voyons maintenant ce qui se passera si l'un des joueurs a de la stabilité. Les nerfs sont des nerfs, un jeu responsable se produit. Supposons, en moyenne, qu'il gagne le même pourcentage de points, mais lorsque vous dessinez un point spécifique, ce pourcentage flotte. Par exemple, la moitié des points sont joués avec la probabilité p1 + delta, et l'autre moitié avec p1-delta. Dans ce cas, la moyenne p1 reste l'original, la perte de + delta ou –delta se produit aléatoirement avec une probabilité de 0,5. Cela affectera-t-il en quelque sorte le résultat du jeu? Comme l'ont montré mes expériences avec l'aide de Monte Carlo, la différence n'est pratiquement pas tracée. En fait, en ajoutant ou en soustrayant un certain montant, bien qu'au hasard, nous restons à la même probabilité moyenne de gagner un point. La suggestion suggère elle-même que la courbe de distribution n'affecte pas le résultat du jeu, mais seulement la moyenne, mais je ne le prendrai pas sur moi. Ici, vous devez réfléchir.
Je voudrais également dériver une équation différentielle, telle que Black Scholes en finance, pour compléter l'association. Identifier les dérivées significatives, mettre à zéro la composante aléatoire ... Nous devons également faire face à la discrétion. Je laisserai peut-être cela aux vrais mathématiciens financiers.