😝 💃 🤛🏻 Julia et l'optimisation 👩🏾‍⚕️ 💃🏿 🕌

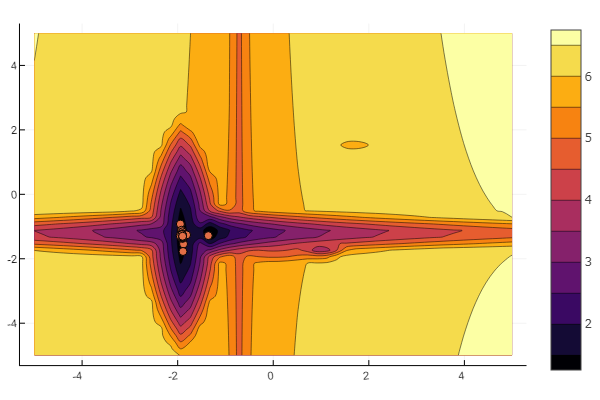
Il est temps d' envisager des packages qui fournissent des méthodes pour résoudre les problèmes d'optimisation. Beaucoup de problèmes peuvent être réduits à trouver le minimum d'une fonction, vous devriez donc avoir un ou deux solveurs dans l'arsenal, et plus encore un package complet.

Entrée

La langue Julia continue de gagner en popularité . Sur https://juliacomputing.com, vous pouvez voir pourquoi les astronomes, la robotique et les financiers choisissent cette langue, et sur https://academy.juliabox.com, vous pouvez commencer des cours gratuits pour apprendre la langue et l'utiliser dans tout type d'apprentissage automatique. Pour ceux qui ont sérieusement décidé de commencer à apprendre, je vous conseille de regarder la vidéo, de lire des articles et de cliquer sur les ordinateurs portables jupiter sur https://julialang.org/learning/ ou au moins de passer par le hub de bas en haut: il y aura une installation, des fonctionnalités et une application pour les entreprises urgent. Passons maintenant aux bibliothèques.

Blackboxoxptim

BlackBoxOptim - package d'optimisation globale pour Julia ( http://julialang.org/ ). Il prend en charge à la fois les problèmes d'optimisation polyvalents et à usage unique et se concentre sur les algorithmes (méta) heuristiques / stochastiques (DE, NES, etc.) qui NE nécessitent PAS que la fonction optimisée soit différenciable, contrairement aux algorithmes déterministes plus traditionnels, qui sont souvent basés sur des gradients / différentiabilité. Il prend également en charge le calcul parallèle pour accélérer l'optimisation des fonctions qui sont évaluées lentement.

Téléchargez et connectez la bibliothèque

]add BlackBoxOptim using BlackBoxOptim

Définissez la fonction Rosenbrock:

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

Nous recherchons un minimum sur l'intervalle (-5; 5) pour chaque coordonnée pour un problème à deux dimensions:

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

Ce que la réponse suivra:

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000

et beaucoup de données illisibles, mais un minimum a été trouvé. Étant donné que stochastique est utilisé, les appels de fonction seront un peu trop, donc pour les tâches multidimensionnelles, il est préférable d'utiliser la sélection des méthodes

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

Convexe

Convex est le package de programmation convexe disciplinaire de Julia (programmation convexe disciplinaire?). Convex.jl peut résoudre des programmes linéaires, des programmes linéaires entiers mixtes et des programmes convexes compatibles DCP à l'aide de divers solveurs, notamment Mosek, Gurobi, ECOS, SCS et GLPK, via l'interface MathProgBase. Il prend également en charge l'optimisation avec des variables et des coefficients complexes.

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS")

Il existe de nombreux exemples sur le site: Tomographie (processus de restauration de la distribution de densité par des intégrales données sur les zones de distribution. Par exemple, vous pouvez travailler avec la tomographie en images noir et blanc), maximiser l'entropie, la régression logistique, la programmation linéaire, etc.

Par exemple, vous devez remplir les conditions:

\ begin {array} {ll} \ mbox {satisf} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}

$\ begin {array} {ll} \ mbox {satisf} & \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {array}$

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value

Donnera une réponse

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783

Sauter

JuMP est un langage d'optimisation mathématique spécifique au domaine intégré à Julia. Il prend actuellement en charge un certain nombre de solveurs ouverts et commerciaux (Artelys Knitro, BARON, Bonmin, Cbc, Clp, Couenne, CPLEX, ECOS, FICO Xpress, GLPK, Gurobi, Ipopt, MOSEK, NLopt, SCS).

JuMP facilite l'identification et la résolution des problèmes d'optimisation sans connaissances d'experts, mais en même temps, il permet aux experts de mettre en œuvre des méthodes algorithmiques avancées, telles que l'utilisation de démarrages à chaud efficaces dans la programmation linéaire ou l'utilisation de rappels pour interagir avec les solveurs de branche et de frontière. JuMP est également rapide - l'analyse comparative a montré qu'elle peut gérer des calculs à des vitesses similaires à des outils commerciaux spécialisés tels que AMPL, tout en conservant l'expressivité d'un langage de programmation universel de haut niveau. JuMP peut être facilement intégré dans des workflows complexes, y compris des simulations et des serveurs Web.

Cet outil vous permet de faire face à des tâches telles que:

LP = programmation linéaire
QP = Programmation quadratique
SOCP = programmation conique du second ordre (y compris les problèmes avec les contraintes quadratiques convexes et / ou le but)
MILP = Programmation linéaire mixte en nombres entiers
PNL = Programmation non linéaire
MINLP = programmation non linéaire d'entiers mixtes
SDP = programmation semi-définie
MISDP = programmation semi-définie d'entiers mixtes

L'analyse de ses capacités sera suffisante pour plusieurs articles, donc pour l'instant passons à ce qui suit:

Optim

Optim Il existe de nombreux solveurs disponibles à la fois à partir de sources gratuites et commerciales, et beaucoup sont déjà emballés pour être utilisés dans Julia. Peu d'entre eux sont écrits dans cette langue. En termes de performances, cela pose rarement problème, car ils sont souvent écrits en Fortran ou en C. Cependant, les solveurs écrits directement en Julia présentent certains avantages.

Lors de l'écriture de logiciels Julia (packages) pour lesquels quelque chose doit être optimisé, le programmeur peut soit écrire sa propre procédure d'optimisation, soit utiliser l'un des nombreux solveurs disponibles. Par exemple, cela pourrait être quelque chose de l'ensemble NLOpt. Cela signifie ajouter une dépendance qui n'est pas écrite dans Julia, et vous devez faire plus d'hypothèses sur l'environnement dans lequel se trouve l'utilisateur. L'utilisateur dispose-t-il de compilateurs appropriés? Puis-je utiliser du code GPL dans un projet?

Il est également vrai que l'utilisation d'un solveur écrit en C ou en Fortran ne permet pas d'utiliser l'un des principaux avantages de Julia: l'envoi multiple. Étant donné qu'Optim est entièrement écrit en Julia, nous pouvons actuellement utiliser un système de répartition pour faciliter l'utilisation des préréglages personnalisés. Une fonctionnalité prévue dans ce sens est de permettre une sélection de solveurs pilotée par l'utilisateur pour les différentes étapes de l'algorithme, basée entièrement sur la répartition plutôt que sur les capacités prédéfinies choisies par les développeurs Optim.

Un package sur Julia signifie également qu'Optim a accès aux fonctions de différenciation automatique via des packages dans JuliaDiff .

Guide

Continuez:

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0)

Nous obtenons une réponse avec un rapport pratique:

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118

Et comparez avec mon Nelder Mead!

spoiler

Le mien sera plus lent :(

Niché

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1

Au cours de la vérification, il s'est également avéré que mon implémentation ne fonctionne pas si vous utilisez l'approximation initiale (0, 0). Comme critère d'arrêt, vous pouvez utiliser le volume du simplexe , mais j'utilise la norme d'une matrice composée de sommets. Ici, vous pouvez lire sur l'interprétation géométrique de la norme. Dans les deux cas, une matrice de zéros est obtenue - un cas particulier d'une matrice dégénérée; par conséquent, la méthode n'effectue aucune étape. Vous pouvez configurer la création d'un simplex de départ, par exemple, en définissant la distance de ses sommets par rapport à l'approximation initiale (et pas comme la mienne - la moitié de la longueur du vecteur, fu, quelle honte ...), puis le paramètre de méthode sera plus flexible, ou assurez-vous que tous les sommets ne sont pas assis à un moment donné:

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end

Eh bien oui, mon simplex goraaazdo est plus lent:

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1

Maintenant plus de raisons de revenir au package d'étude

Vous pouvez choisir la méthode utilisée:

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67

et obtenez une documentation détaillée et des références

 ?LBFGS()

Vous pouvez définir des fonctions jacobiennes et hessoises

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14

Comme vous pouvez le voir, il a automatiquement élaboré la méthode Newton. Et donc vous pouvez définir la zone de recherche et utiliser la descente de gradient:

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382

Eh bien, ou je ne sais pas, disons que vous vouliez résoudre l'équation

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8

et il vous a choisi la méthode Brent .
Ou ayant des données expérimentales, vous devez optimiser les coefficients du modèle

F (p_{1}, p_{2}, x) = p_{1} c o s (p_{2} x) + p_{2} s i n (p_{1} x)

$F (p_1, p_2, x) = p_1 \ cos (p_2x) + p_2 \ sin (p_1x)$

p_{1} = 1, p_{2} = 0, 2

$p_1 = 1, p_2 = 0,2$

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y)

Bonus Créez votre fonction de test

L' idée est reprise de l'article de Khabrov . Vous pouvez configurer vous-même chaque minimum local:

 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Et vous pouvez tout laisser à la volonté du tout-puissant aléatoire

 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

Mais comme vous pouvez le voir sur la photo de départ, un essaim de particules avec un tel relief n'est pas intimidant.

Cela devrait être fait. Comme vous pouvez le voir, Julia dispose d'un environnement mathématique assez puissant et moderne qui permet des recherches numériques complexes sans se pencher sur des abstractions de programmation de bas niveau. Et c'est une excellente occasion de continuer à étudier cette langue.

Bonne chance à tous!