Dans cet article, je présente une nouvelle séquence quasi aléatoire à faible divergence qui offre une amélioration significative par rapport aux séquences modernes, telles que Sable, Niederreiter, etc.Figure 1. Comparaison de diverses séquences quasi aléatoires avec une faible divergence. Notez que le proposé par moi R -séquence crée des points plus uniformément répartis que toutes les autres méthodes. De plus, toutes les autres méthodes nécessitent une sélection minutieuse des paramètres de base et, en cas de sélection incorrecte, conduisent à la dégénérescence (par exemple, en haut à droite)Sujets traités dans cet article- Séquences à faible divergence en une dimension
- Méthodes de faible divergence en deux dimensions
- Distance d'emballage
- Ensembles multiclasses à faible écart
- Séquences quasi aléatoires à la surface d'une sphère
- Carrelage plan quasi-périodique
- Masques de tramage en infographie
Il y a quelque temps, ce message a été publié sur la page d'accueil de Hacker News. Vous pouvez y lire sa
discussion .
Introduction: aléatoire versus quasi aléatoire
Dans la figure 1, vous pouvez remarquer qu'avec un simple échantillonnage aléatoire uniforme d'un point à l'intérieur d'un carré unitaire, une accumulation de points est observée, ainsi que des zones sans points («bruit blanc»). Une
séquence quasi aléatoire à
faible divergence est une méthode de construction (infinie) de points consécutifs de manière déterministe, qui réduit la probabilité d'accumulation (divergence), tout en assurant une couverture uniforme de tout l'espace («bruit bleu»).
Séquences quasi-aléatoires en une dimension
Les méthodes pour créer des séquences quasi aléatoires complètement déterminées avec une faible divergence dans une dimension sont très bien étudiées et résolues en termes généraux. Dans cet article, je vais principalement considérer les séquences ouvertes (infinies), d'abord dans une dimension, puis passer à des dimensions plus élevées. L'avantage fondamental des séquences ouvertes (c'est-à-dire extensibles en
n ) réside dans le fait que si les erreurs totales basées sur un nombre fini de membres sont trop grandes, alors la séquence peut être étendue sans ignorer tous les points calculés précédents. Il existe de nombreuses façons de créer des séquences ouvertes. Vous pouvez diviser différents types en catégories par la méthode de construction de leurs paramètres (hyper) de base:
- fractions irrationnelles: Kronecker, Richtmayer, Ramshaw
- (mutuellement) nombres premiers: Van der Corpute, Holton, Foret
- Polynômes irréductibles: Niederreiter
- Polynômes primitifs: sable
Par souci de concision, dans cet article, je comparerai principalement le nouvel additif
récursif R - une séquence qui appartient à la première catégorie, c'est-à-dire aux méthodes récursives basées sur des nombres irrationnels (souvent appelés séquences de Kronecker,
Weil ou Richtmeier), qui sont des réseaux de rang 1, et une séquence de Holton, qui est basée sur la séquence canonique unidimensionnelle de van der Corpute. La séquence récursive canonique de Kronecker est définie comme suit:
R_1 (\ alpha): \; \; t_n = \ {s_0 + n \ alpha \}, \ quad n = 1,2,3, ...
où
alpha - tout numéro irrationnel. Notez que l'entrée
\ {x \} désigne la partie fractionnaire
x . Dans les calculs, cette fonction est souvent exprimée comme
R1( alpha):tn=s0+n alpha( textrmmod1); quadn=1,2,3,...
À
s0=0 premiers membres de la séquence
R( phi) égal à:
tn=0,618,0,236,0,854,0,472,0,090,0,708,0,327,0,944,0,562,0,180,798,416,0,034,0,652,0,271,0,888,...
Il est important de noter que le sens
s0 n'affecte pas les caractéristiques générales de la séquence, et dans presque tous les cas est égal à zéro. Cependant, dans le calcul de l'option
s neq0 offre un degré de liberté supplémentaire, ce qui est souvent utile. Si
s neq0 , alors la séquence est souvent appelée «séquence de réseau décalé». Malgré le fait que par défaut
s=0 Je crois qu'il y a des considérations théoriques et pratiques pour lesquelles la valeur devrait être standard
s=1/2 . Valeur
alpha donnant le plus petit écart possible si
alpha=1/ phi où
phi - C'est le nombre d'or. C’est
phi equiv frac sqrt5+12 simeq1.61803398875...;
Il est intéressant de noter qu'il existe un nombre infini d'autres valeurs.
alpha , qui nous permettent également d'obtenir l'écart optimal, et ils sont tous liés les uns aux autres par la transformation Mobius
alpha′= fracp alpha+qr alpha+s quad textrmpourtouslesentiersp,q,r,s quad textrmtelque|ps−qr|=1
Nous comparons maintenant cette méthode récursive avec les séquences bien connues de van der Korput avec ordre inverse des décharges [
van der Korput, 1935 ]. Les séquences de Van der Corpute sont en fait une famille de séquences, chacune étant définie par un hyperparamètre unique
b . Les premiers membres de la séquence avec b = 2 sont égaux:
t[2]n= frac12, frac14, frac34, frac18, frac58, frac38, frac78, frac116, frac916, frac516, frac1316, frac316, frac1116, frac716, frac1516,...
Dans la section suivante, nous comparons les caractéristiques générales et l'efficacité de chacune de ces séquences. Considérez le problème du calcul d'une certaine intégrale
A= int10f(x) textrmdx
Nous pouvons l'approcher comme:
A simeqAn= frac1n sumni=1f(xi), quadxi in[0,1]
- Si \ {x_i \} sont égaux i/n , c'est la formule des rectangles ;
- Si \ {x_i \} sélectionné au hasard, alors c'est la méthode de Monte Carlo ; mais
- Si \ {x_i \} sont des éléments d'une séquence avec une faible divergence, alors c'est la méthode quasi-Monte Carlo .
Le graphique ci-dessous montre les courbes d'erreur typiques.
sn=|A−An| pour approximer une certaine intégrale associée à cette fonction,
f(x)= textrmexp( frac−x22),x dans[0,1] pour: (i) des points quasi-aléatoires de récursion additive, où
alpha=1/ phi , (bleu); (ii) des points quasi aléatoires de la séquence de van der Corput, (orange); (iii) des points choisis au hasard, (vert); (iv) Séquences de sable (rouge).
Cela montre que pour
n=106 une solution de points avec échantillonnage aléatoire conduit à une erreur
simeq10−4 , la séquence de van der Corput mène à une erreur
simeq10−6 , alors que
R( phi) - la séquence conduit à une erreur
simeq10−7 que dans
sim 10 fois mieux que l'erreur de van der Corput et
sim 1000 fois mieux qu'un échantillonnage aléatoire (uniforme).
Figure 2. Comparaison de l'intégration numérique unidimensionnelle à l'aide de diverses méthodes Monte Carlo quasi aléatoires. Plus la valeur est basse, mieux c'est. Nouveau R2 - la séquence (bleue) et la séquence de sable (rouge) sont évidemment les meilleures.Les éléments suivants méritent d'être mentionnés ici:
- cela correspond à la connaissance que les erreurs d'échantillonnage aléatoire uniforme diminuent asymptotiquement 1/ sqrtn , et l'erreur pour les deux séquences quasi-aléatoires a tendance à
 .
. - Résultats pour R1( phi) -les séquences (bleues) et les séquences de sable (rouge) sont les meilleures.
- Le graphique montre que la séquence van der Corpute fournit de bons résultats, mais incroyablement cohérents pour les tâches d'intégration!
- On peut voir ici que pour toutes les valeurs n séquence R1( phi) donne de meilleurs résultats que la séquence de van der Corput.
Nouvelle séquence R1 , qui est la séquence de Kronecker utilisant le nombre d'or, est l'une des meilleures options pour les méthodes d'intégration Monte Carlo quasi-aléatoires unidimensionnelles (Quasirandom Monte Carlo, QMC).
Il convient également de noter que, bien que
alpha= phi fournit théoriquement une option prouvée optimale,
sqrt2 très proche de l'optimal, et presque toute autre valeur irrationnelle
alpha fournit des courbes d'erreur supérieures pour une intégration unidimensionnelle. C'est pourquoi il est très souvent utilisé
alpha= sqrtp pour tout nombre premier. De plus, du point de vue des calculs, la valeur aléatoire choisie dans l'intervalle
alpha in[0,1] ce sera presque certainement (dans les limites de la précision de la machine) un nombre irrationnel, et est donc un bon choix pour une séquence avec une faible divergence. Pour la lisibilité visuelle, la figure ci-dessus ne montre pas les résultats de la séquence Niederreiter, car ils sont pratiquement indiscernables des résultats des séquences Sobol et
R . Les séquences Niederreiter et Sable (ainsi que leur sélection optimisée de paramètres) qui ont été utilisées dans cet article ont été calculées dans Mathematica en utilisant ce que l'on appelle des "générateurs propriétaires fermés et entièrement optimisés de la bibliothèque Intel MKL" dans la documentation.
Séquences quasi-aléatoires en deux dimensions
La plupart des méthodes modernes pour construire une faible variance dans des dimensions plus élevées se combinent simplement (composant par composant)
d séquences unidimensionnelles. Par souci de concision, dans ce post, nous considérerons principalement la séquence de
Holton [
Holton, 1960 ], la séquence de Sable et
d -Séquence de Kronecker dimensionnelle.
La séquence de Holton est construite à l'aide de simples
d diverses séquences van der Corpute unidimensionnelles, dont la base est mutuellement simple pour toutes les autres. Autrement dit, ce sont des nombres premiers par paire. Sans aucun doute, l'option la plus courante en raison de sa simplicité et de sa logique évidentes est le choix du premier
d nombres premiers. La distribution des 625 premiers points définis par la séquence Holton (2,3) est illustrée à la figure 1. Bien que de nombreuses séquences Holton bidimensionnelles soient d'excellentes sources de séquences à faible divergence, il est bien connu que bon nombre d'entre elles sont très problématiques et ne présentent pas de faible divergence. Par exemple, la figure 3 montre que la séquence de Holton (11,13) génère des lignes très visibles. De grands efforts ont été déployés pour développer des méthodes de sélection des modèles et des paires problématiques.
(p1,p2) . Dans des dimensions supérieures, le problème devient encore plus compliqué.
Lors de la généralisation à des dimensions supérieures, les méthodes récursives de Kronecker rencontrent des difficultés encore plus grandes. Bien qu'en utilisant
alpha= sqrtp d'excellentes séquences unidimensionnelles sont créées, il est extrêmement difficile de trouver même des paires de nombres premiers pouvant servir de base à un cas bidimensionnel
qui ne pose
pas de problème! Il a été suggéré d'utiliser d'autres nombres irrationnels bien connus comme solution de contournement, par exemple
phi, pi,e,... . Ils fournissent des résultats modérément acceptables, mais ne sont généralement pas utilisés, car ils ne sont généralement pas aussi bons qu'une séquence Holton correctement sélectionnée. De gros efforts sont faits pour résoudre ces problèmes de dégénérescence.
Les solutions proposées utilisent le saut / gravure, le saut / amincissement. Et pour le codage (brouillage) des séquences finales, une autre technique est utilisée, souvent utilisée pour surmonter ce problème. Le brouillage ne peut pas être utilisé pour créer une séquence ouverte (infinie) avec une faible divergence.
Figure 3. La séquence (11,13) -Holton n'est évidemment pas une séquence à faible divergence (à gauche). Ce n'est pas non plus une séquence additive récursive (11,13) (au milieu). Certaines séquences récursives additives bidimensionnelles qui utilisent des nombres irrationnels bien connus sont plutôt bonnes (à droite).De même, malgré les résultats généralement meilleurs de la séquence de Sable, sa complexité et, plus important encore, la nécessité d'une sélection très attentive des hyperparamètres la rend moins conviviale.
Encore une fois, dans
d mesures:
- les séquences Kronecker typiques nécessitent un choix d nombres irrationnels linéairement indépendants;
- La séquence Holton nécessite d entiers mutuellement premiers par paire; mais
- La séquence de sable nécessite un choix d nombres guides.
Nouvelle séquence Rd - le seul d -séquence quasi aléatoire dimensionnelle avec une faible divergence, ne nécessitant pas un choix de paramètres de base.
Généralisation du nombre d'or
tl; dr Dans cette partie, je vais parler de la façon de construire une nouvelle classe
d - séquence ouverte (infinie) dimensionnelle à faible divergence, ne nécessitant pas un choix de paramètres de base, ayant d'excellentes propriétés de faible divergence.
Il existe de nombreuses façons de généraliser la séquence de Fibonacci et / ou le nombre d'or. La méthode proposée ci-dessous pour généraliser le nombre d'or
n'est pas nouvelle [
Krchadinac, 2005 ]. De plus, le polynôme caractéristique est associé à de nombreuses zones d'algèbre, y compris les
nombres de Perron et les
nombres de Piso-Vijayaraghavan . Cependant, le lien explicite entre cette forme généralisée et la construction de séquences de grande dimension avec une faible divergence est nouveau en elle. Nous définissons une vision généralisée du nombre d'or
phid comme une racine positive unique
xd+1=x+1 . Autrement dit,
Pour
d=1 ,
phi1=1.61803398874989484820458683436563... , qui est le nombre d'or canonique.
Pour
d=2 ,
phi2=1,32471795724474602596090885447809... . Cette valeur est souvent appelée constante plastique et possède de
belles propriétés (voir également
ici ). On suppose que cette valeur est très probablement optimale pour le problème bidimensionnel correspondant [
Hensley, 2002 ].
Pour
d=3 ,
phi3=1,220744084605759475361685349108831...Pour
d>3 , bien que les racines de cette équation n'aient pas de forme algébrique fermée, nous pouvons facilement obtenir une approximation numérique soit par des méthodes standard, par exemple, la méthode de Newton, soit en notant que pour la séquence suivante
Rd( phid) :
t0=t1=...=td=1;
tn+d+1=tn+1+tn, quad textrmforn=1,2,3,..
Cette séquence particulière de constantes
phid a été nommé en 1928 par l'architecte et moine Hans van de Laan comme "
nombres harmoniques ". Ces significations spéciales peuvent être exprimées très élégamment comme suit:
phi1= sqrt1+ sqrt1+ sqrt1+ sqrt1+ sqrt1+...
\ phi_2 = \ sqrt [3] {1+ \ sqrt [3] {1+ \ sqrt [3] {1+ \ sqrt [3] {1+ \ sqrt [3] {1 + ...}}}}}}
\ phi_3 = \ sqrt [4] {1+ \ sqrt [4] {1+ \ sqrt [4] {1+ \ sqrt [4] {1+ \ sqrt [4] {1 + ...}}}}}}
Nous avons également la propriété très élégante suivante:
phid= limn to infty fractn+1tn
Cette séquence, parfois appelée séquence de Fibonacci généralisée ou différée, a été étudiée en profondeur [
As, 2004 ,
Wilson, 1993 ], et la séquence de
d=2 souvent appelée séquence Padovan [
Stuart, 1996 ,
OEIS A000931 ], et la séquence
d=3 répertorié dans [
OEIS A079398 ]. Comme indiqué ci-dessus, la tâche principale de cet article est de décrire le lien explicite entre cette séquence généralisée et la construction
d -séquences dimensionnelles à faible divergence.
Résultat principal: le non paramétrique suivant d -dimensionnelle séquence ouverte (infinie) Rd( phid) présente d'excellentes caractéristiques de faible écart par rapport aux autres méthodes existantes.
\ mathbf {t} _n = \ {n \ pmb {\ alpha} \}, \ quad n = 1,2,3, ...
textrmwhere quad pmb alpha=( frac1 phid, frac1 phi2d, frac1 phi3d,... frac1 phidd)
textrmet phid textrmestuneracinepositiveuniquexd+1=x+1
Pour deux dimensions, cette séquence généralisée pour
n=150 comme le montre la figure 1. Les points sont évidemment répartis de façon beaucoup plus
R2 -séquences que dans les séquences (2, 3) -Holton, séquences de Kronecker basées sur
( sqrt3, sqrt7) , Niederreiter et Sable. (En raison de la complexité des séquences Niederreiter et Sable, elles ont été calculées dans Mathematica à l'aide d'un code propriétaire fourni par Intel.) Ce type de séquence dans lequel le vecteur de base
pmb alpha est fonction d'une seule valeur matérielle, souvent appelée séquence de Korobov [Korobov, 1959]
Regardez de nouveau la figure 1 pour comparer diverses séquences quasi aléatoires bidimensionnelles à faible divergence.Code et démos
Dans une dimension, pseudo-code pour
n membre (
n = 1,2,3, ....) est défini comme
g = 1.6180339887498948482 a1 = 1.0/g x[n] = (0.5+a1*n) %1
En deux dimensions, le pseudo-code des coordonnées
x et
yn membre (
n = 1,2,3, ....) Sont définis comme
g = 1.32471795724474602596 a1 = 1.0/g a2 = 1.0/(g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1
Pseudocode en trois dimensions pour les coordonnées
x ,
y et
zn membre (
n = 1,2,3, ....) est défini comme
g = 1.22074408460575947536 a1 = 1.0/g a2 = 1.0/(g*g) a3 = 1.0/(g*g*g) x[n] = (0.5+a1*n) %1 y[n] = (0.5+a2*n) %1 z[n] = (0.5+a3*n) %1
Modèle de code Python. (notez que les tableaux et les boucles Python partent de zéro!)
import numpy as np
J'ai écrit le code de manière à ce qu'il corresponde à la notation mathématique utilisée dans ce post. Cependant, pour des raisons de conventions de programmation et / ou d'efficacité, certaines modifications méritent d'être mentionnées. Premièrement, depuis
R2 est une séquence
récursive additive, formulation alternative
z qui ne nécessite pas de multiplication en virgule flottante et maintient une grande précision pour les très grandes
n a la forme
z[i+1] = (z[i]+alpha) %1
Deuxièmement, dans les langages vectorisables, le code d'une fonction fractionnaire peut être vectorisé comme suit:
for i in range(n): z[i] = seed + alpha*(i+1) z = z %1
Enfin, nous pouvons remplacer ces ajouts de nombres à virgule flottante et entiers en multipliant toutes les constantes par
232 , puis en modifiant la fonction frac (.) en conséquence. Voici les démos de code source créées par d'autres personnes sur la base de cette séquence:
Distance minimale d'emballage
Nouveau R2 -séquence est la seule séquence quasi aléatoire bidimensionnelle avec une faible divergence dans laquelle la distance de compactage minimale est réduite uniquement à 1/ sqrtn .
Bien que l'analyse technique standard du calcul de l'écart consiste à évaluer
d∗ - divergences, nous mentionnerons d'abord quelques autres méthodes géométriques (et, peut-être, beaucoup plus intuitives!) pour montrer à quel point la nouvelle séquence est préférable à d'autres méthodes standard. Si nous dénotons la distance entre les points
i et
j pour
dij et
d0= textrminfdij le tableau ci-dessous montre comment il varie
d0(n) pour
R -séquences, (2,3) - Séquences Holton, Sable, Niederreiter et séquences aléatoires. Cela peut être vu dans la figure 6.
Comme dans la figure précédente, la valeur de distance minimale est normalisée par le coefficient
1/ sqrtn . Vous remarquerez peut-être qu'après
n=300 des points dans une séquence aléatoire (vert) apparaissent presque certainement deux points qui sont extrêmement proches l'un de l'autre. On voit également que, bien que la séquence de Holton (2,3) soit bien meilleure que l'échantillonnage aléatoire, elle diminue malheureusement également de façon asymptotique jusqu'à zéro. Pour la séquence de sable, la raison de la normalisation diminue à zéro
d0 réside dans le fait que
Sable lui-même a montré que
la séquence de
Sable tombe à une vitesse
/n - ce qui est bien, mais évidemment bien pire que
R2 qui ne diminue que de
1/ sqrtn .
Pour séquence
R( phi2) (bleu) la distance minimale entre deux points tombe constamment dans l'intervalle de

avant

. A noter que le diamètre optimal de 0,868 correspond à un facteur de remplissage de 59,2%. Comparez cela avec d'autres
emballages de cercles .
Notez également que l'
échantillonnage du disque de Bridson Poisson , qui n'est
pas extensible à
n et est généralement recommandé par défaut, il crée toujours un facteur d'emballage de 49,4%. Il convient de considérer que le concept
d0 lie étroitement les séquences
phid faible divergence avec des nombres / vecteurs peu
d mesures [
Hensley, 2001 ]. Bien que nous en sachions peu sur les nombres mal approchés en deux dimensions, la construction
phid peut nous fournir un nouveau regard sur des nombres mal approchés dans des dimensions plus élevées.
Figure 4. Distance par paire minimale pour diverses séquences à faible divergence. Notez que R2 - la séquence (bleue) est toujours la meilleure option; de plus, c'est la seule séquence dans laquelle la distance normalisée n'a pas tendance à zéro à n rightarrow infty . La séquence de Holton (orange) prend la deuxième place, et les séquences de sable (vert) et de Niederreiter (rouge) ne sont pas si bonnes, mais toujours bien mieux que aléatoires (violet). Plus c'est grand, mieux c'est, car cela correspond à une distance d'emballage plus longue.Diagrammes de Voronoi
Une autre façon de visualiser la distribution uniforme des points est de créer un diagramme de Voronoi à partir du premier
n points d'une séquence bidimensionnelle avec coloration ultérieure de chaque zone en fonction de sa
zone . La figure ci-dessous montre les nuanciers Voronoi pour (i)
R2 -séquences; (ii) (2,3) séquences de Holton, (iii) récursion principale; et (iv) un échantillonnage aléatoire simple. Pour toutes les figures, utilisez la même échelle de couleurs. Là encore, il est évident que
R2 La séquence fournit une distribution beaucoup plus uniforme que la séquence de Holton ou un simple échantillonnage aléatoire. L'image est la même que ci-dessus, colorée uniquement en fonction du nombre de sommets dans chaque cellule de Voronoi. Il n'est pas seulement évident ici que
R - la séquence fournit une distribution plus uniforme que Holton ou un échantillonnage aléatoire simple, mais le fait que les valeurs clés sont plus visibles
n se composent uniquement d'hexagones! Si nous considérons la séquence de Fibonacci généralisée, alors
A1=A2=A3=1; quadAn+3=An+1+An . C’est
An :
$$ afficher $$ \ begin {array} {r} 1 & 1 & 1 & 2 & 2 & 3 & 4 & 5 & 7 \\ 9 & \ textbf {12} & 16 & 21 & 28 & 37 & \ textbf {49} & 65 & 86 \\ 114 & \ textbf {151 } & 200 & 265 & 351 & 465 & \ textbf {616} & 816 & 1081 \\ 1432 & \ textbf {1897} & 2513 & 3329 & 4410 & 5842 & \ textbf {7739} & 10252 & 13581 \\ 17991 & \ textbf {23833} & 31572 & 41824 & 55405 & 7 {97229} & 128801 & 170625 \\ 226030 & \ textbf {299426} & 396655 & 525456 & 696081 & 922111 & \ textbf {1221537} & 1618192 & 2143648 \\ \ end {array} $$ display $$
Toutes les valeurs dans lesquelles
n=A9k−2 ou
n=A9k+2 se composent uniquement d'hexagones.
Figure 4. Visualisation de la forme des diagrammes de Voronoi en fonction de l'aire de chaque polygone de Voronoi pour (i) R2 -séquences; (ii) (2,3) - séquences basées sur des nombres premiers; (iii) la séquence (2,3) de Holton, (iv) Niederraiter; (v) Sable; et (iv) un échantillonnage aléatoire simple. Les couleurs indiquent le nombre de côtés de chaque polygone Voronoi. Je le répète: il est évident que R( phi) -séquence fournit une distribution beaucoup plus uniforme que toute autre séquence avec une faible divergence.À certaines valeurs n Grille Voronoi pour R2 -séquence se compose uniquement d'hexagones.
Figure 5. Visualisation de la forme des diagrammes de Voronoi en fonction du nombre de côtés de chaque polygone de Voronoi pour (i) R2 -séquences; (ii) (2,3) - séquences basées sur des nombres premiers; (iii) la séquence (2,3) de Holton, (iv) Niederraiter; (v) Sable; et (iv) un échantillonnage aléatoire simple. Les couleurs indiquent le nombre de côtés de chaque polygone Voronoi. Je le répète: il est évident que R( phi) -séquence fournit une distribution beaucoup plus uniforme que toute autre séquence avec une faible divergence.Mosaïque quasi-aléatoire de Delaunay pour un avion
R -séquence est la seule séquence quasi aléatoire à faible divergence qui peut être utilisée pour créer d pavages quasipériodiques tridimensionnels utilisant son maillage Delaunay.
La triangulation de Delaunay, qui est similaire au comte Voronoi, offre une opportunité de regarder ces distributions différemment. Cependant, plus important encore, la triangulation de Delaunay fournit une nouvelle méthode pour créer un pavage quasi-périodique (mosaïque) d'un plan. Triangulation de Delaunay
R2 -séquences fournit un modèle beaucoup plus uniforme qu'une séquence de Holton ou un échantillonnage aléatoire. En particulier, si la triangulation de Delaunay des distributions ponctuelles est effectuée, où
n égal à l'une des séquences de Fibonacci généralisées:
AN=$1,1,1,2,3,4,5,7,9,12,16,21,28,37,... , alors la triangulation de Delaunay se compose de seulement trois triangles identiques, c'est-à-dire de parallélogrammes (rhomboïdes)! (Sauf pour les triangles qui ont un sommet commun avec une coque convexe.) De plus,
Aux valeurs n=Ak Triangulation de Delaunay R2 -séquences forme des pavages quasipériodiques, chacun composé de seulement trois triangles de base (rouge, jaune, bleu), qui sont toujours connectés par paires et forment un pavage quasipériodique bien défini (pavage) du plan avec trois parallélogrammes (rhomboïdes).
Figure 6. Visualisation de la triangulation de Delaunay pour (i) R( phi2) -séquences; (ii) (2,3) séquences de Holton, (iii) récursion principale; et (iv) un échantillonnage aléatoire simple. Les couleurs indiquent l'aire de chaque triangle. Les quatre graphiques utilisent la même échelle. Et là encore, il est évident que R( phi2) -séquence fournit une distribution beaucoup plus uniforme que toute autre séquence avec une faible divergence.Notez que
R2 basé sur
phi2=1,32471795724474602596 étant le plus petit nombre de piso, (un
phi=1,61803... Est le plus grand nombre de pisos). La connexion du carrelage quasi-périodique avec des nombres quadratiques et cubiques de Piso n'est pas nouvelle [
Elkharrat et Masakova], mais je crois que pour la première fois, le carrelage quasi-périodique a été créé sur la base de
phi2=1,324719... .
L'animation ci-dessous montre comment le maillage Delaunay pour la séquence
R2 changements avec l'ajout progressif de points. Notez que lorsque le nombre de points est égal à un membre de la séquence de Fibonacci généralisée, alors la grille de Delaunay entière n'est constituée que de parallélogrammes (rhomboïdes) rouges, bleus et jaunes, disposés sous une double forme quasi-périodique.
Bien que la disposition des parallélogrammes rouges démontre une régularité considérable, on peut clairement voir que les parallélogrammes bleu et jaune sont placés sous une forme quasi-périodique. Le spectre de Fourier de ce réseau peut être vu sur la figure 11, il représente les spectres ponctuels classiques. (Notez qu'une séquence récursive basée sur des nombres premiers semble également quasi-périodique dans le sens où il s'agit d'un motif ordonné non répétitif. Cependant, son motif dans l'intervalle
n pas si constant, et dépend également de manière critique du choix des paramètres de base. Par conséquent, nous ne concentrerons notre intérêt pour les pavages quasipériodiques que par la séquence
R2 .) Il se compose de seulement trois triangles: rouge, jaune, bleu. Notez que dans cette séquence
R( phi2) tous les parallélogrammes de chaque couleur ont la même taille et la même forme. Le rapport d'aspect de ces triangles individuels est incroyablement élégant. À savoir
textrmZone(rouge):Zone(jaune):Zone(bleu)=1: phi2: phi22
Il en va de même pour la fréquence relative des triangles:
f( textrmred):f( textrmyellow):f( textrmblue)=1: phi2:1
Il en résulte que l'aire relative totale couverte par ces trois triangles dans l'espace est:
f( textrmred):f( textrmyellow):f( textrmblue)=1: phi22: phi22
On peut également supposer que nous pouvons créer ce pavage quasi-périodique par substitution basée sur la séquence A.
A rightarrowB; quadB rightarrowC; quadC rightarrowBA
Pour trois dimensions, si nous considérons la séquence de Fibonacci généralisée, alors
B1=B2=B3=B4=1; quadBn+4=Bn+1+Bn . C’est
B_n = \ {1,1,1,1,2,2,2,3,4,4,5,7,8,9,12,15,17,21,27,32,38,48,59 , 70,86,107,129, ...
À certaines valeurs n=Bk Maillage 3D Delaunay associé à une séquence R3 , définit un réseau cristallin quasi-périodique.
Emballage discrétisé, partie 2
La figure ci-dessous montre le premier
n=2500 points pour chaque séquence bidimensionnelle à faible divergence. De plus, chacune des cellules 50 × 50 = 2500 n'est colorée en vert que si elle contient
exactement 1 point. Autrement dit, plus les carrés sont verts, plus la distribution de 2500 points dans 2500 cellules est uniforme. Le pourcentage de cellules vertes pour chacun des chiffres est le suivant:
R2 (75%), Holton (54%), Kronecker (48%), Niederreiter (54%), Sable (49%) et aléatoire (38%).
Ondes sonores
Juste pour le plaisir, à la demande d'
un lecteur de News Hacker, j'ai modélisé comment toutes ces distributions de points quasi-aléatoires peuvent
sonner ! J'ai utilisé la fonction Listplay de Mathematica: "
ListPlay [{a1, a2, ...}] crée un objet qui se reproduit sous forme de son, dont l'amplitude est donnée comme une séquence de niveaux." Par conséquent, sans aucun commentaire, je vous laisse décider par vous-même lesquelles vous préférez parmi les distributions quasi-aléatoires unidimensionnelles (mono) et les distributions quasi-aléatoires bidimensionnelles (stéréo).
| Mono | Stéréo |
|---|
| Aléatoire | | |
| Sable | | |
| Niederreiter | | |
| Holton | | |
| Kronecker | | |
| R | | |
Ensembles multiclasses à faible écart
Certaines séquences à faible divergence démontrent ce qu'on appelle une «faible divergence multi-classe». Jusqu'à ce moment, nous avons supposé que lorsque nous devons distribuer le plus uniformément possible
n points, alors tous les points sont les mêmes et ne se distinguent pas les uns des autres. Cependant, dans de nombreuses situations, il existe différents types de points. Nous considérons le problème de la distribution uniforme
n de sorte que non seulement tous les points sont répartis uniformément, mais aussi les points de la même classe. En particulier, supposons qu'il existe
nk taper des points
k , (où
n1+n2+n3+...+nk=n ), alors la distribution du multiset avec une distribution faible est une distribution dans laquelle chaque
nk points uniformément répartis. Dans notre cas, nous avons constaté que
R -La séquence et la séquence Holton sont faciles à adapter aux séquences de multisets à faible divergence, simplement en plaçant alternativement des points de chaque type.
La figure ci-dessous montre comment ils sont distribués
n=150 les points, tandis que 75 sont bleus, 40 sont poivrés, 25 sont verts et 10 sont rouges. Pour une séquence récursive additive, cela est résolu trivialement: les 75 premiers membres correspondent simplement au bleu, les 40 suivants à l'orange, les 25 suivants au vert et les 10 derniers aux points rouges. Cette technique fonctionne presque pour les séquences Holton et Kronecker, mais fonctionne très mal dans les séquences Niederreiter et Sable. De plus, il n'existe aucune technique connue pour la génération continue de distributions ponctuelles multi-échelles dans les séquences de Niederreiter et de Sable. Cela montre que les
distributions de points multiclasses , par exemple, comme les
yeux des poulets , peuvent maintenant être décrites et construites directement à l'aide de séquences à faible divergence.
Séquence R2 Est une séquence quasi aléatoire à faible divergence qui permet de construire facilement une faible divergence à plusieurs classes.
Figure 9. Séquences multi-échelles avec faible divergence. En séquence R non seulement tous les points sont répartis uniformément, mais aussi les points de chaque couleur individuelle.Points quasi aléatoires sur une sphère
Dans les domaines de l'infographie et de la physique, il est souvent nécessaire de répartir aussi uniformément que possible les points à la surface d'une sphère tridimensionnelle. Lorsque vous utilisez des séquences quasi-aléatoires ouvertes (infinies), ce problème se réduit uniquement à placer des points quasi-aléatoires uniformément répartis dans un carré unitaire à la surface de la sphère en utilisant la projection égale de Lambert. Transformation de projection standard de Lambert en plaçant un point
(u,v) inU[0,1] to(x,y,z) inS2 a la forme:
(x,y,z)=( cos lambda cos phi, cos lambda sin phi, sin lambda)
textrmoù quad cos( lambda− pi/2)=(2u−1); quad phi=2 piv
Depuis
phi2 -la séquence est complètement ouverte, elle vous permet d'aligner une séquence infinie de points à la surface de la sphère, un point à la fois. Cela contraste avec d'autres méthodes, comme le
réseau de la spirale de Fibonacci , qui nécessitent de connaître à l'avance le nombre de points. En ce qui concerne l'inspection visuelle, nous pouvons à nouveau clairement voir que
n=1200 nouveau
R( phi2) - La séquence est beaucoup mieux répartie que l'échantillonnage par superposition Holton ou l'échantillonnage Kronecker, qui, à son tour, est beaucoup plus uniforme que l'échantillonnage aléatoire.
Figure 10Infiltration d'infographie
La plupart des techniques de tramage modernes (par exemple, le tramage Floyd-Steinberg) sont basées sur la distribution des erreurs, ce qui n'est pas très approprié pour le traitement parallèle et / ou l'optimisation directe dans le GPU. Dans de tels cas, le tramage ponctuel avec des masques de tramage statiques (c'est-à-dire complètement dépendants de l'image cible) présente d'excellentes caractéristiques de performance. Les masques de tramage les plus célèbres et les plus utilisés sont probablement basés sur des matrices
Bayer , mais les plus récents tentent de simuler de plus près les caractéristiques du bruit bleu. La difficulté non triviale de créer des masques de tramage basés sur des séquences à faible divergence et / ou bruit bleu est que ces séquences à faible divergence projettent un entier
Z à un point à deux dimensions dans l'intervalle
[0,1)2 .
Mais pour un masque de tramage, une fonction est requise qui projette les coordonnées entières bidimensionnelles du masque tramé en valeur de luminosité / seuil réelle dans l'intervalle [0,1) .
Je suggère l'approche suivante basée sur R-séquences. Pour chaque pixel (x, y) du masque, nous attribuons sa valeur de luminositéI(x,y) où:I(x,y)=α1x+α2y(mod1);
αα=(α1,α2)=(1ϕ2,1ϕ22)
ϕ2 - x3=x+1
C’est x=1.32471795724474602596… , ce qui signifieα1=0.75487766624669276;α2=0.569840290998
De plus, si une fonction d'onde triangulaire est ajoutée pour éliminer la discontinuité causée par la fonction frac (.) Sur chaque frontière entière:T(z)={2z,if 0≤z<1/22−2z,if1/2≤z<1
I(x,y)=T[α1x+α2y(mod1)];
puis le masque et son diagramme de Fourier / fréquence sont encore améliorés. Nous notons également que depuislimn→∞AnAn+1=0.754878;limn→∞AnAn+2=0.56984
alors la forme de l'expression ci-dessus est liée à l'équation congruente suivanteAnx+An+1y(modAn+2) for integers x,y
Les masques R tramés créent des résultats qui rivalisent avec les méthodes modernes basées sur les masques de bruit bleu. Mais contrairement aux masques de bruit bleu, ils n'ont pas besoin d'être calculés à l'avance, car ils peuvent être calculés en temps réel.
Il convient de noter que cette structure a également été proposée par Mittring , mais il trouve les coefficients empiriquement (et ne reproduit pas les valeurs finales). De plus, cela aide à comprendre pourquoi la formule empirique de Jorge Jimenez utilisée pour créer «Call of Duty» (souvent appelé «Interleaved Gradient Noise») fonctionne si bien .I(x,y)=(FractionalPart[52.9829189∗FractionalPart[0.06711056∗x+0.00583715∗y]]
Cependant, il nécessite 3 multiplications à virgule flottante et deux opérateurs% 1, et la formule précédente montre que nous pouvons le faire avec seulement deux multiplications à virgule flottante et une opération% 1. Mais plus important encore, cet article fournit une compréhension mathématique plus claire de la raison pour laquelle un masque de tramage sous cette forme est si efficace, sinon optimal. Les résultats de cette matrice de tramage sont présentés ci-dessous en utilisant l'image de test classique Lena 256 × 256 ainsi qu'un modèle de test d'échecs. Il montre également les résultats de l'utilisation de masques de tramage Bayer standard, ainsi qu'un exemple avec du bruit bleu. Les deux méthodes de bruit bleu les plus courantes sont l'échantillonnage à disque vide et à grappes et Poisson. Par souci de concision, je n'ai montré que les résultats de la méthode Void et cluster. [ Peters]. Le bruit de gradient entrelacé fonctionne mieux que le bruit de Bayer et bleu, mais pas aussi bon queRtramage. Vous pouvez voir que le tramage Bayer montre une dissonance notable de blanc dans les zones gris clair. DitheringR- la séquence et le bruit bleu sont généralement comparables, bien que des différences mineures puissent être constatées. Il convient de noter certains aspects du tramage R:- Il n'est pas isotrope! Les spectres de Fourier ne montrent que des points individuels et discrets. Il s'agit d'une caractéristique classique des pavages quasipériodiques et des spectres de diffraction des quasi-cristaux. En particulier, les spectres de Fourier pourR Les masques correspondent au fait que la triangulation de Delaunay pour la séquence R canonique consiste en un pavage quasi-périodique de trois parallélogrammes.
- Le tramage R lorsqu'il est combiné avec une onde triangulaire fournit un masque incroyablement uniforme!
- R- , .
- , , R- , .
- (I(x,y) , .
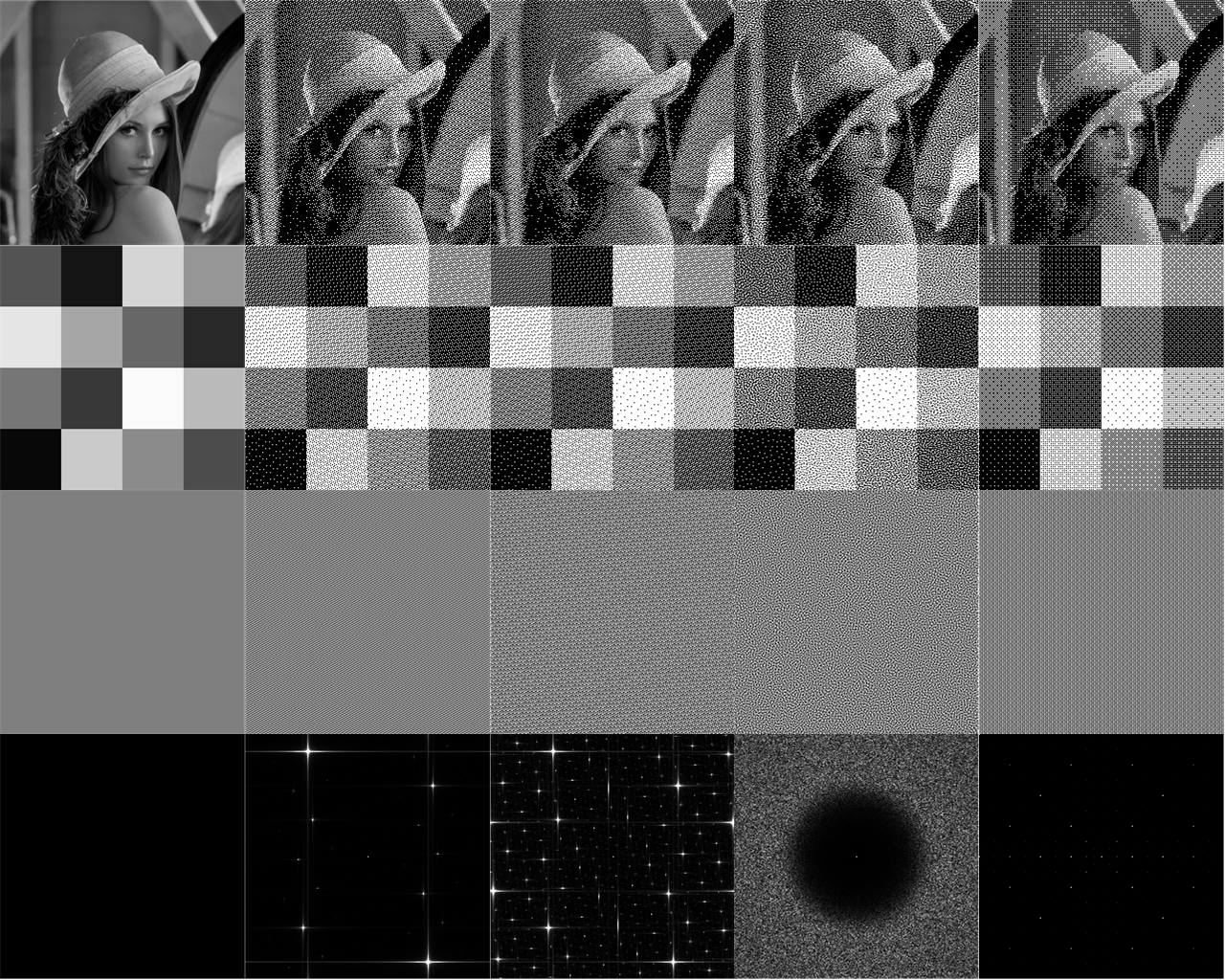
Dimensions supérieures
Semblable à la section précédente, mais pour cinq (5) mesures, le graphique ci-dessous montre la distance minimale (globale) entre deux points R(ϕ5)-séquences, (2,3,5,7,11) -séquences de Holton et séquences aléatoires. Cette fois, la valeur normalisée de la distance minimale est normalisée par un facteur1/5√n .
Vous pouvez voir qu'en raison de la «malédiction des dimensions», la distribution aléatoire est meilleure que toutes les séquences à faible divergence - à l'exception de R5 -séquences. Dans
R(ϕ5) -séquences même avec n≃106 points, la distance minimale entre deux points est toujours constamment proche 0.8/√n et toujours plus haut 0.631/√n .
Séquence R2 - le seul d -séquence dimensionnelle à faible divergence, dans laquelle la distance d'emballage commence à diminuer uniquement avec la vitesse n−1/d .
Figure 12. Cela montre que la séquence R (bleue) est toujours meilleure que Holton (orange); Sable (vert); Niederreiter (rouge); et aléatoire (violet). Gardez à l'esprit que plus c'est grand, mieux c'est, car cela correspond à une distance d'emballage plus longue.Intégration numérique
Le graphique suivant montre les courbes d'erreur typiques. sn=|A−An| pour approcher une certaine intégrale associée à une fonction gaussienne demi-largeur σ=√d ,
f(x)=exp(−x22d),x∈[0,1] , tandis que: (i) Rϕ(bleu); (ii) séquence Holton (orange); (iii) aléatoire (vert); (iv) Sable (rouge). Le graphique montre que pourn=106il y a maintenant moins de différences entre l'échantillonnage aléatoire et la séquence de Holton. Cependant, comme cela a été montré dans le cas unidimensionnel,R- Séquence et Sable sont toujours meilleurs que la séquence de Holton. Cela nous permet également de savoir que la séquence de Sable est légèrement meilleure.R -séquences.Figure 13. Méthodes quasi aléatoires de Monte Carlo pour l'intégration à 8 dimensions. Plus la valeur est basse, mieux c'est. La nouvelle séquence R et la nouvelle séquence Sable se montrent beaucoup mieux que la séquence Holton.