Un autre week-end est venu, ce qui signifie que j'écris quelques dizaines de lignes de code et que j'en fais une ou deux illustrations. Dans des articles précédents, j'ai expliqué comment faire le lancer de rayons et même faire exploser des trucs . Cela peut vous surprendre, mais l'infographie est assez simple: même quelques centaines de lignes de C ++ nu peuvent produire des images très excitantes.

Le sujet d'aujourd'hui est la vision binoculaire, et nous ne briserons même pas la barrière des 100 lignes en le faisant. Étant donné que nous pouvons dessiner des scènes 3D, il serait stupide d'ignorer les paires stéréo, alors aujourd'hui, nous allons créer quelque chose comme ceci:




La folie pure des créateurs de Magic Carpet me souffle encore. Pour ceux qui ne le savent pas, ce jeu vous a permis de faire un rendu 3D en mode anaglyphe et stéréogramme depuis le menu principal des paramètres ! C'était fou pour moi.

Parallax

Alors, commençons. Pour commencer, qu'est-ce qui fait que notre appareil de vision perçoit la profondeur dans les objets? Il y a un terme intelligent de «parallaxe». Concentrons-nous sur l'écran. Tout ce qui se trouve dans le plan de l'écran est enregistré par notre cerveau comme étant un seul objet. Mais si une mouche vole entre nos yeux et l'écran, le cerveau la perçoit comme deux objets. L'araignée derrière l'écran sera également doublée.



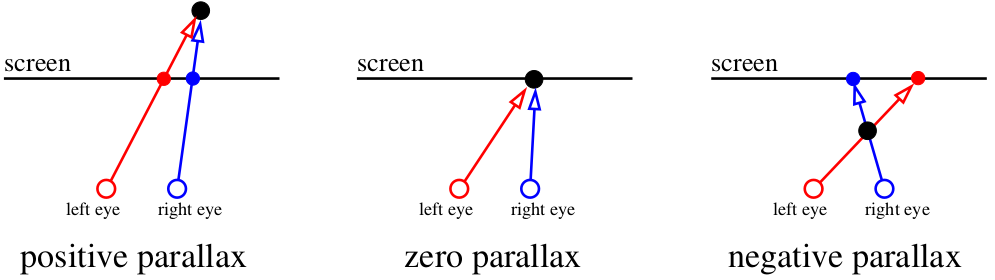
Notre cerveau est très efficace pour analyser des images légèrement différentes. Il utilise la disparité binoculaire pour obtenir des informations sur la profondeur des images 2D provenant de la rétine en utilisant une stéréopsie . Eh bien, vissez les gros mots et dessinons des images!

Imaginons que notre moniteur soit une fenêtre sur le monde virtuel :)



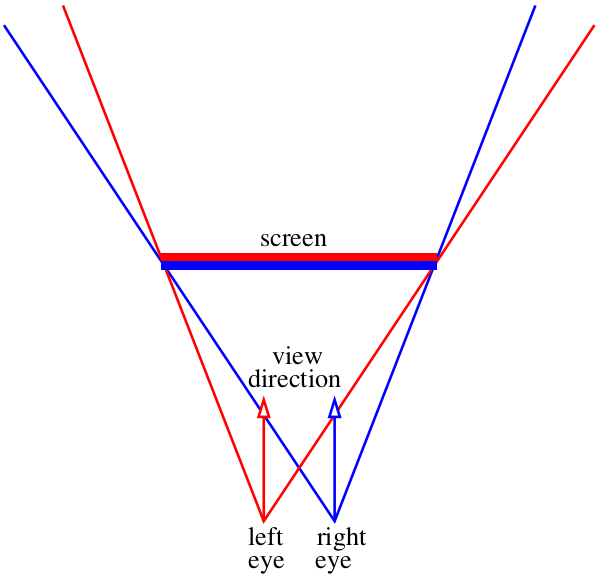
Notre tâche consiste à dessiner deux images de ce que nous voyons à travers cette «fenêtre», une pour chaque œil. Sur la photo ci-dessus, le "sandwich" rouge-bleu. Oublions pour l'instant comment délivrer ces images à notre cerveau, à ce stade, nous avons juste besoin d'enregistrer deux fichiers distincts. En particulier, je veux savoir comment obtenir ces images en utilisant mon minuscule raytracer .

Supposons que l'angle ne change pas et que c'est le vecteur (0,0, -1). Supposons que nous puissions déplacer la caméra dans la zone située entre les yeux, mais alors quoi? Un petit détail: la vue tronconique à travers notre «fenêtre» est asymétrique. Mais notre traceur de rayons ne peut que rendre un tronc symétrique:



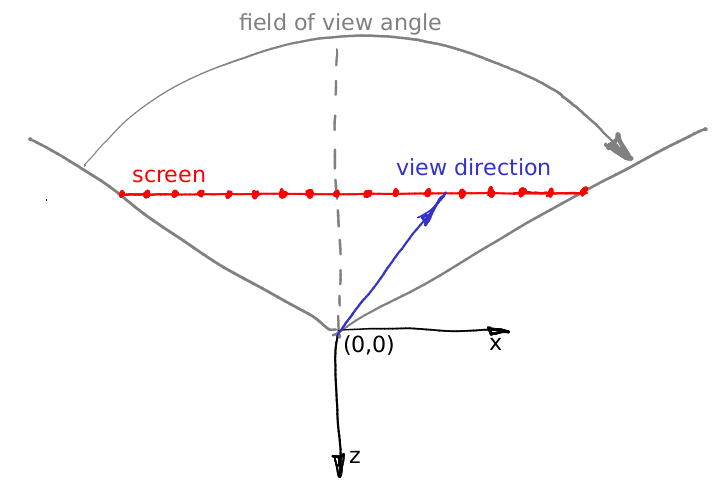
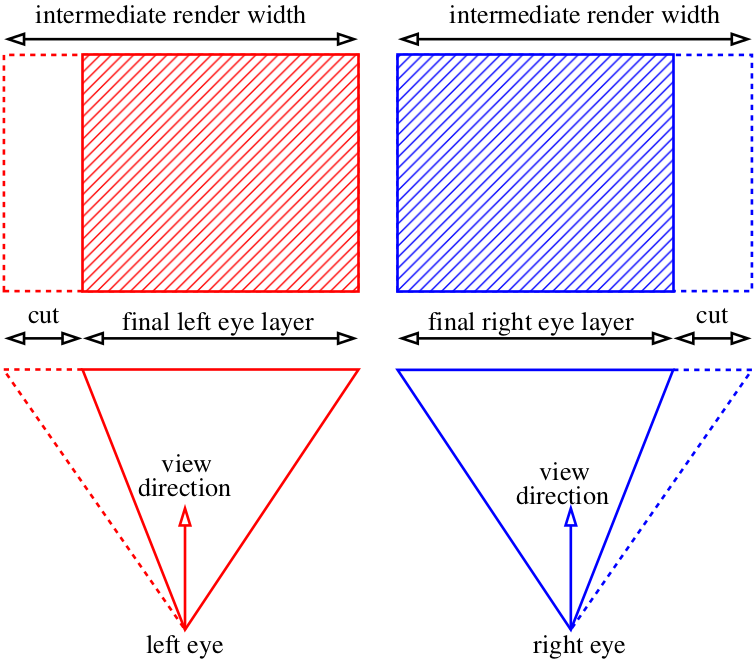
Et qu'est-ce qu'on fait maintenant? Tricher :)

Nous pouvons rendre des images légèrement plus larges que ce dont nous avons besoin, puis découper les parties supplémentaires:

Anaglyphe

Je pense que nous avons couvert le mécanisme de rendu de base, et maintenant nous abordons la question de la livraison de l'image à notre cerveau. La manière la plus simple est ce type de lunettes:



Nous réalisons deux rendus en niveaux de gris et attribuons des images gauche et droite respectivement aux canaux rouge et bleu. Voici ce que nous obtenons:



Le verre rouge coupe un canal, tandis que le verre bleu coupe l'autre. Combinés, les yeux obtiennent une image différente et nous la percevons en 3D. Voici les modifications apportées au commit principal à partir du tinyraytracer. Les changements incluent le positionnement de la caméra pour les yeux et l'assemblage des canaux.

Le rendu anaglyphe est l'un des moyens les plus anciens de regarder des images stéréo (générées par ordinateur). Il présente de nombreux inconvénients, par exemple une mauvaise transmission des couleurs. Mais d'un autre côté, ceux-ci sont très faciles à créer à la maison.

Si vous n'avez pas de compilateur sur votre ordinateur, ce n'est pas un problème. Si vous avez un compte guithub, vous pouvez visualiser, éditer et exécuter le code (sic!) En un clic dans votre navigateur.



Lorsque vous ouvrez ce lien, gitpod crée une machine virtuelle pour vous, lance VS Code et ouvre un terminal sur la machine distante. Dans l'historique des commandes (cliquez sur la console et appuyez sur la touche haut), il y a un ensemble complet de commandes qui vous permet de compiler le code, de le lancer et d'ouvrir l'image résultante.

Stéréoscope

Les smartphones étant devenus courants, nous nous sommes souvenus de l'invention du XIXe siècle appelée stéréoscope. Il y a quelques années, Google a suggéré d'utiliser deux lentilles (qui, malheureusement, sont difficiles à créer à la maison, vous devez l'acheter), un peu de carton (disponible partout) et un smartphone (dans votre poche) pour créer plutôt crédible Lunettes VR.



Ils sont nombreux sur AliExpress et coûtent environ 3 $ la paire. Par rapport au rendu anaglyphe, nous n'avons même pas trop à faire: il suffit de prendre deux photos et de les mettre côte à côte. Voici le commit .



À strictement parler, en fonction de l'objectif, nous pourrions avoir besoin de corriger la distorsion de l'objectif , mais je ne me suis pas soucié de cela, car cela avait l'air bien malgré tout. Mais si nous devons vraiment appliquer la pré-distorsion en barillet qui compense la distorsion naturelle de l'objectif, c'est à quoi cela ressemble pour mon smartphone et mes lunettes:



Voici le lien gitpod:

Autostéréogrammes

Et que faisons-nous si nous ne voulons pas utiliser d'équipement supplémentaire? Ensuite, il n'y a qu'une seule option - plisser les yeux. La photo précédente, honnêtement, est assez suffisante pour une visualisation stéréo, plissez simplement les yeux (en croisant les yeux ou en les murant). Voici un schéma qui nous indique comment regarder l'illustration précédente. Deux lignes rouges montrent les images perçues par la rétine gauche, deux bleues - la rétine droite.



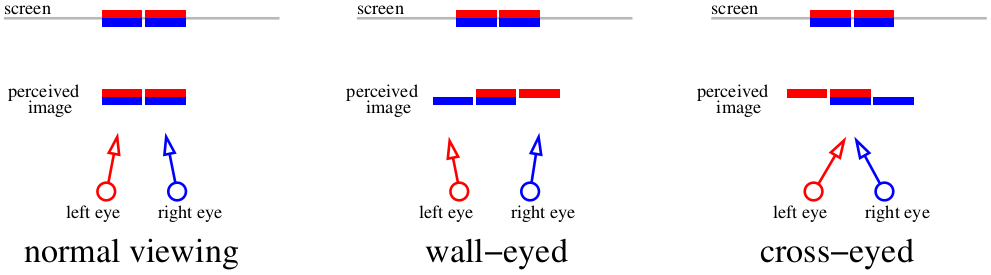
Si nous nous concentrons sur l'écran, quatre images se combinent en deux. Si nous croisons les yeux ou si nous nous concentrons sur un objet éloigné, il est possible de nourrir le cerveau «trois» images. Les images centrales se chevauchent, ce qui crée l'effet stéréo.

Différentes personnes utilisent des méthodes différentes: par exemple, je ne peux pas croiser les yeux, mais les cloisonner facilement. Il est important que l'autostéréogramme construit pour une certaine méthode ne soit visualisé qu'avec cette méthode, sinon nous obtenons une carte de profondeur inversée (rappelez-vous la parallaxe positive et négative?). Le problème est qu'il est difficile de beaucoup croiser les yeux, donc cela ne fonctionne que sur de petites images. Et si nous en voulons de plus gros? Sacrifions entièrement les couleurs et concentrons-nous uniquement sur la partie perception de la profondeur. Voici l'image que nous espérons obtenir d'ici la fin de l'article:



Ceci est un autostéréogramme aux yeux muraux. Pour ceux qui préfèrent l'autre méthode, voici une image pour cela . Si vous n'êtes pas habitué aux autostéréogrammes, essayez différentes conditions: plein écran, image plus petite, luminosité, obscurité. Notre objectif est de cloisonner nos yeux afin que les deux bandes verticales proches se chevauchent. Le plus simple est de se concentrer sur la partie supérieure gauche de l'image, car c'est clair. Personnellement, j'ouvre l'image en plein écran. N'oubliez pas de retirer également le curseur de la souris!

Ne vous arrêtez pas à un effet 3D incomplet. Si vous voyez vaguement des formes arrondies et que l'effet 3D est faible, l'illusion est incomplète. Les sphères sont censées «sauter» hors de l'écran vers le spectateur, l'effet doit être stable et durable. La stéréopsie a une gisteresis: une fois que vous obtenez une image stable, elle devient plus détaillée plus vous l'observez. Plus les yeux sont éloignés de l'écran, plus l'effet de perception de la profondeur est grand.

Ce stéréogramme a été dessiné en utilisant une méthode suggérée il y a 25 ans dans cet article: " Affichage d'images 3D: algorithmes pour les stéréogrammes à points aléatoires à image unique ".

Commençons

Le point de départ du rendu des autostéréogrammes est la carte de profondeur (puisque nous abandonnons les couleurs). Cette validation dessine l'image suivante:



Les plans de plus en plus rapprochés définissent notre profondeur: le point le plus éloigné de ma carte a la profondeur de 0, tandis que le plus proche a la profondeur de 1.

Les principes de base

Disons que nos yeux sont à une distance d de l'écran. Nous plaçons notre plan lointain (imaginaire) (z = 0) à la même distance «derrière» l'écran. Nous choisissons la variable μ, qui détermine l'emplacement du plan proche (z = 1), qui sera à une distance μd du plan lointain. Pour mon code, j'ai choisi μ = ⅓. Dans l'ensemble, notre «monde» entier vit à distance de d-μd à d derrière l'écran. Disons que nous connaissons la distance entre les yeux (en pixels, j'ai choisi 400 pixels):



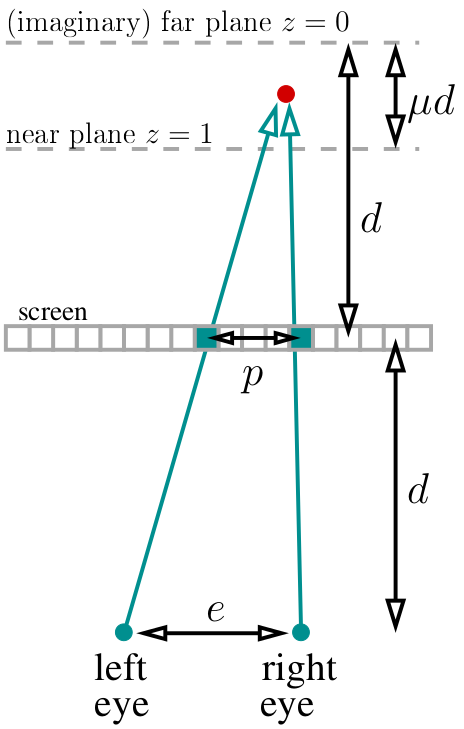
Si nous regardons le point rouge, alors deux pixels marqués en vert devraient avoir la même couleur dans le stéréogramme. Comment calculer la distance entre eux? Facile Si le point projeté actuel a la profondeur de z, alors la parallaxe divisée par la distance entre les yeux est égale à la fraction entre les profondeurs correspondantes: p / e = (d-dμz) / (2d-dμz). Soit dit en passant, d est simplifié et n'apparaît nulle part ailleurs! Ensuite, p / e = (1-μz) / (2-μz), ce qui signifie que la parallaxe est égale à p = e * (1-μz) / (2-μz) pixels.

L'idée principale derrière l'autostéréogramme est la suivante: nous parcourons l'intégralité de la carte de profondeur, pour chaque valeur de profondeur, nous déterminons quels pixels auront la même couleur et la déposerons dans notre système de contraintes. Ensuite, nous partons de l'image aléatoire et essayons de satisfaire toutes les contraintes que nous avons définies précédemment.

Préparation de l'image source

Ici, nous préparons l'image qui sera plus tard contrainte par des contraintes de parallaxe. Voici le commit , et il dessine ceci:



Notez que les couleurs sont principalement aléatoires, à l'exception du canal rouge où j'ai mis rand () * sin pour créer un motif périodique. Les bandes sont distantes de 200 pixels, ce qui (étant donné μ = 1/3 et e = 400) la valeur de parallaxe maximale dans notre monde (le plan lointain). Le motif n'est pas techniquement nécessaire, mais cela aidera à concentrer les yeux.

Rendu autostéréogramme

En fait, le code complet qui dessine l'autostéréogramme ressemble à ceci:

int parallax(const float z) { const float eye_separation = 400.; // interpupillary distance in pixels const float mu = .33; // if the far plane is a distance D behind the screen, then the near plane is a distance mu*D in front of the far plane return static_cast<int>(eye_separation*((1.-z*mu)/(2.-z*mu))+.5); } size_t uf_find(std::vector<size_t> &same, size_t x) { return same[x]==x ? x : uf_find(same, same[x]); } void uf_union(std::vector<size_t> &same, size_t x, size_t y) { if ((x=uf_find(same, x)) != (y=uf_find(same, y))) same[x] = y; } int main() { [...] for (size_t j=0; j<height; j++) { // autostereogram rendering loop std::vector<size_t> same(width); std::iota(same.begin(), same.end(), 0); // initialize the union-find data structure (same[i]=i) for (size_t i=0; i<width; i++) { // put the constraints int par = parallax(zbuffer[i+j*width]); int left = i - par/2; int right = left + par; // works better than i+par/2 for odd values of par if (left>=0 && right<(int)width) uf_union(same, left, right); // left and right pixels will have the same color } for (size_t i=0; i<width; i++) { // resolve the constraints size_t root = uf_find(same, i); for (size_t c=0; c<3; c++) framebuffer[(i+j*width)*3+c] = framebuffer[(root+j*width)*3+c]; } } [...] 

Voici la validation , la fonction int parallaxe (const float z) nous donne la distance entre les pixels de la même couleur pour la valeur de profondeur actuelle. Nous rendons le stéréogramme ligne par ligne, car les lignes sont indépendantes les unes des autres (nous n'avons pas de parallaxe verticale). La boucle principale parcourt simplement chaque ligne; chaque fois qu'il démarre avec un ensemble illimité de pixels, puis pour chaque pixel il ajoute une contrainte d'égalité. Au final, cela nous donne un certain nombre de clusters de pixels de même couleur. Par exemple, les pixels avec des index gauche et droit devraient finir identiques.

Comment stocker cet ensemble de contraintes? Le moyen le plus simple est la structure de données union-find . Je n'entrerai pas dans les détails, allez simplement sur Wikipedia, c'est littéralement trois lignes de code. Le point principal est que pour chaque cluster, il y a un certain pixel «racine» responsable du cluster. Le pixel racine conserve sa couleur initiale et tous les autres pixels du cluster doivent être mis à jour:

  for (size_t i=0; i<width; i++) { // resolve the constraints size_t root = uf_find(same, i); for (size_t c=0; c<3; c++) framebuffer[(i+j*width)*3+c] = framebuffer[(root+j*width)*3+c]; } 

Conclusion

Voilà, vraiment. Vingt lignes de code et notre autostéréogramme sont prêts à vous en casser les yeux. Soit dit en passant, si nous essayons assez fort, il est possible de transmettre des informations sur les couleurs.

Je n'ai pas couvert d'autres systèmes stéréoscopiques comme les systèmes 3D polarisés , car ils sont beaucoup plus chers à fabriquer. Si j'ai raté quelque chose, n'hésitez pas à me corriger!