Programmation relationnelle: douleur, intérêt et douleur à nouveau

Dans le post précédent, nous avons expliqué en détail ce que nous enseignons aux étudiants dans le domaine de la "programmation industrielle". Pour ceux dont le domaine d'intérêt se situe dans un domaine plus théorique, par exemple, attiré par les nouveaux paradigmes de programmation ou les mathématiques abstraites utilisées dans la recherche théorique sur la programmation, il existe une autre spécialisation - «Langages de programmation».

Aujourd'hui je vais vous parler de mes recherches dans le domaine de la programmation relationnelle, que je fais à l'université et en tant qu'étudiant-chercheur au laboratoire des outils linguistiques JetBrains Research.

Qu'est-ce que la programmation relationnelle? Habituellement, nous exécutons une fonction avec des arguments et obtenons le résultat. Et dans le cas relationnel, vous pouvez faire le contraire: corriger le résultat et un argument, et obtenir le deuxième argument. L'essentiel est d'écrire le code correctement et d'être patient et d'avoir un bon cluster.

À propos de moi

Je m'appelle Dmitry Rozplohas, je suis un étudiant de première année du HSE de Saint-Pétersbourg, et l'année dernière j'ai obtenu mon diplôme du programme de baccalauréat de l'Université académique dans le domaine des «langages de programmation». Depuis la troisième année d'études de premier cycle, je suis également étudiante de recherche au laboratoire d'outils linguistiques JetBrains Research.

Programmation relationnelle

Faits généraux

La programmation relationnelle, c'est quand, au lieu de fonctions, vous décrivez la relation entre les arguments et le résultat. Si le langage est affiné pour cela, vous pouvez obtenir certains bonus, par exemple, la possibilité d'exécuter la fonction dans le sens opposé (restaurer les valeurs possibles des arguments en conséquence).

En général, cela peut être fait dans n'importe quel langage logique, mais l'intérêt pour la programmation relationnelle est apparu simultanément avec l'avènement d'un miniKanren en langage logique pur minimaliste il y a une dizaine d'années, ce qui a permis de décrire et d'utiliser commodément de telles relations.

Voici certains des cas d'utilisation les plus avancés: vous pouvez écrire un vérificateur de preuve et l'utiliser pour trouver des preuves ( Near et al., 2008 ) ou créer un interpréteur pour une langue et l'utiliser pour générer des programmes de suite de tests ( Byrd et al., 2017 ).

Exemple de syntaxe et de jouet

miniKanren est un petit langage; seules les constructions mathématiques de base sont utilisées pour décrire les relations. Il s'agit d'un langage intégré, ses primitives sont une bibliothèque pour certains langages externes et de petits programmes miniKanren peuvent être utilisés dans un programme dans une autre langue.

Langues étrangères adaptées à miniKanren, tout un tas. Initialement, il y avait Scheme, nous travaillons avec la version pour Ocaml ( OCanren ), et la liste complète peut être consultée sur minikanren.org . Les exemples de cet article concerneront également OCanren. De nombreuses implémentations ajoutent des fonctions d'assistance, mais nous nous concentrerons uniquement sur le langage principal.

Commençons par les types de données. Classiquement, ils peuvent être divisés en deux types:

• Les constantes sont des données du langage dans lequel nous sommes intégrés. Chaînes, nombres, même tableaux. Mais pour le miniKanren de base, tout cela est une boîte noire, l'égalité des constantes ne peut être vérifiée.
  
• Un «terme» est un tuple de plusieurs éléments. Couramment utilisé de la même manière que les constructeurs de données dans Haskell: constructeur de données (chaîne) plus zéro ou plusieurs paramètres. OCanren utilise des constructeurs de données réguliers d'OCaml.
  

Par exemple, si nous voulons travailler avec des tableaux dans miniKanren lui-même, alors il doit être décrit en termes de termes similaires aux langages fonctionnels - comme une liste liée individuellement. Une liste est soit une liste vide (indiquée par un terme simple), soit une paire du premier élément de la liste («tête») et d'autres éléments («queue»).

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil))) 

Un programme miniKanren est la relation entre certaines variables. Au démarrage, le programme donne toutes les valeurs possibles des variables sous une forme générale. Souvent, les implémentations vous permettent de limiter le nombre de réponses dans la sortie, par exemple, ne trouvez que la première - la recherche ne s'arrête pas toujours après avoir trouvé toutes les solutions.

Vous pouvez écrire plusieurs relations définies les unes par rapport aux autres et même appelées de manière récursive en tant que fonctions. Par exemple, ci-dessous, nous au lieu de la fonction $$$append (a, b) → avec$définir la relation $$$appendo (a, b, c)$: liste $$$c$est une concaténation de listes $$$a$et $$$b$. Les fonctions qui renvoient des relations se terminent traditionnellement par un «o» pour les distinguer des fonctions ordinaires.

Une relation est écrite comme une déclaration concernant ses arguments. Nous avons quatre opérations de base :

• Unification ou égalité (===) de deux termes, les termes peuvent inclure des variables. Par exemple, vous pouvez écrire la relation «liste $$$l$se compose d'un élément $$$x$":
  
  

   let isSingletono xl = l === Cons (x, Nil) 

• Conjonction (logique «et») et disjonction (logique «ou») - comme dans la logique ordinaire. OCanren sont appelés &&& et |||. Mais il n'y a fondamentalement aucun déni logique dans MiniKanren.
  
• Ajout de nouvelles variables. En logique, c'est un quantificateur d'existence. Par exemple, pour vérifier la liste de non-vide, vous devez vérifier que la liste se compose d'une tête et d'une queue. Ce ne sont pas des arguments de la relation, vous devez donc créer de nouvelles variables:
  
  

   let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 

Une relation peut s'invoquer récursivement. Par exemple, vous devez définir l'élément "relation" $$$x$se trouve sur la liste. " Nous allons résoudre ce problème en analysant des cas triviaux, comme dans les langages fonctionnels:

1. Ou la tête de liste est $$$x$
   
2. Soit $$$x$se trouve dans la queue
   

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) ) 

La version de base du langage est construite sur ces quatre opérations. Il existe également des extensions qui vous permettent d'utiliser d'autres opérations. Le plus utile d'entre eux est la contrainte de déséquilibre pour fixer l'inégalité de deux termes (= / =).

Malgré le minimalisme, miniKanren est un langage assez expressif. Par exemple, regardez la concaténation relationnelle de deux listes. La fonction de deux arguments se transforme en une triple relation " $$$ab$est une concaténation de listes $$$a$et $$$b$".

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb))) 

La solution n'est pas structurellement différente de la façon dont nous l'écririons dans un langage fonctionnel. Nous analysons deux cas unis par une clause:

1. Si la première liste est vide, la deuxième liste et le résultat de la concaténation sont égaux.
   
2. Si la première liste n'est pas vide, alors nous l'analysons dans la tête et la queue et construisons le résultat en utilisant un appel récursif de la relation.
   

Nous pouvons faire une demande à cette relation, en fixant le premier et le deuxième argument - nous obtenons la concaténation des listes:

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q) 

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil)))) 

Nous pouvons corriger le dernier argument - nous obtenons toutes les partitions de cette liste en deux.

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil))))) 

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil 

Vous pouvez faire autre chose. Un exemple légèrement plus non standard, dans lequel nous ne corrigeons qu'une partie des arguments:

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil)))))) 

⇒

 q = 2, r = Cons (3, Cons (4, Nil)) 

Comment ça marche

Du point de vue de la théorie, il n'y a rien d'impressionnant ici: vous pouvez toujours simplement commencer à rechercher toutes les options possibles pour tous les arguments, en vérifiant pour chaque ensemble s'ils se comportent par rapport à une fonction / relation donnée comme nous le souhaiterions (voir "The British Museum Algorithm" ) . Il est intéressant de noter qu'ici, la recherche (en d'autres termes, la recherche d'une solution) utilise uniquement la structure de la relation décrite, grâce à laquelle elle peut être relativement efficace dans la pratique.

La recherche est en relation avec l'accumulation d'informations sur diverses variables dans l'état actuel. Soit nous ne savons rien de chaque variable, soit nous savons comment elle est exprimée en termes, valeurs et autres variables. Par exemple:

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

En passant par l'unification, nous examinons deux termes avec ces informations à l'esprit et mettons à jour l'état ou terminons la recherche si deux termes ne peuvent pas être unifiés. Par exemple, en complétant l'unification b = c, nous obtenons de nouvelles informations: x = 10, y = z. Mais l'unification b = Nil provoquera une contradiction.

Nous recherchons les conjoints de manière séquentielle (afin que les informations s'accumulent), et dans une disjonction, nous divisons la recherche en deux branches parallèles et continuons, en alternant les étapes en elles - c'est ce que l'on appelle la recherche entrelacée. Grâce à cette alternance, la recherche est terminée - chaque solution appropriée sera trouvée après un temps limité. Par exemple, dans le langage Prolog, ce n'est pas le cas. Il fait quelque chose comme une exploration profonde (qui peut s'accrocher à une branche infinie), et la recherche entrelacée est essentiellement une modification de l'analyse large délicate.

Voyons maintenant comment fonctionne la première requête de la section précédente. Puisque appendo a des appels récursifs, nous ajouterons des index aux variables pour les distinguer. La figure ci-dessous montre l'arbre d'énumération. Les flèches indiquent le sens de diffusion de l'information (à l'exception du retour de récursivité). Entre les disjonctions, l'information n'est pas distribuée, et entre les conjonctions est distribuée de gauche à droite.

1. Nous commençons par un appel externe à appendo. La branche gauche de la disjonction décède en raison d'une controverse: liste $$$a$pas vide.
   
2. Dans la branche de droite, des variables auxiliaires sont introduites, qui sont ensuite utilisées pour «analyser» la liste $$$a_1$sur la tête et la queue.
   
3. Après cela, l'appel récursif appendo se produit pour a = [2], b = [3, 4], ab = ?, dans lequel des opérations similaires se produisent.
   
4. Mais dans le troisième appel à appendo, nous avons déjà a = [], b = [3,4], ab =?, Puis la disjonction gauche fonctionne, après quoi nous obtenons les informations ab = b. Mais dans la bonne branche, il y a une contradiction.
   
5. Nous pouvons maintenant écrire toutes les informations disponibles et restaurer la réponse en substituant les valeurs des variables:
   
   a_1 = [1, 2]
b_1 = [3, 4]
ab_1 = Cons h_1 tb_1
h_1 = 1
a_2 = t_1 = [2]
b_2 = b_1 = [3, 4]
ab_2 = tb_1 = Cons h_2 tb_2
h_2 = 2
a_3 = t_2 = Nil
b_3 = b_2 = b_1 = [3, 4]
ab_3 = tb_2 = b_3 = [3, 4]

   
6. Il s'ensuit que $$$ab_1$= Contre (1, Contre (2, [3, 4])) = [1, 2, 3, 4], selon les besoins.
   

Ce que j'ai fait au premier cycle

Tout ralentit

Comme toujours: ils vous promettent que tout sera super déclaratif, mais en réalité, vous devez vous adapter à la langue et tout écrire de manière spéciale (en gardant à l'esprit comment tout sera exécuté) afin qu'au moins quelque chose fonctionne, à l'exception des exemples les plus simples. C'est décevant.

L'un des premiers problèmes auxquels est confronté un programmeur débutant de miniKanren est qu'il dépend beaucoup de l'ordre dans lequel vous décrivez les conditions (conjoints) dans le programme. Avec une seule commande, tout va bien, mais deux conjonctions ont été échangées et tout a commencé à fonctionner très lentement ou n'a pas fini du tout. C'est inattendu.

Même dans l'exemple avec appendo, le lancement dans la direction opposée (générant la division de la liste en deux) ne se termine pas sauf si vous spécifiez explicitement le nombre de réponses que vous souhaitez (alors la recherche se terminera une fois le nombre requis trouvé).

Supposons que nous fixions les variables d'origine comme suit: a = ?, B = ?, Ab = [1, 2, 3] (voir la figure ci-dessous) Dans la deuxième branche, ces informations ne seront en aucun cas utilisées lors d'un appel récursif (la variable ab et les restrictions sur $$$h_1$et $$$tb_1$n'apparaissent qu'après cet appel). Par conséquent, au premier appel récursif, tous ses arguments seront des variables libres. Cet appel générera toutes sortes de triplets à partir de deux listes et de leur concaténation (et cette génération ne se terminera jamais), puis parmi eux seront choisis ceux pour lesquels le troisième élément s'est avéré exactement la façon dont nous avons besoin.



Tout n'est pas aussi mauvais que cela puisse paraître à première vue, car nous allons trier ces triplets en grands groupes. Les listes avec la même longueur mais des éléments différents ne diffèrent pas du point de vue de la fonction, donc elles tomberont dans une solution - il y aura des variables libres à la place des éléments. Néanmoins, nous allons toujours trier toutes les longueurs de liste possibles, bien que nous n'en ayons besoin que d'une seule, et nous savons laquelle. Il s'agit d'une utilisation très irrationnelle (non-utilisation) des informations dans la recherche.

Cet exemple spécifique est facile à corriger: il vous suffit de déplacer l'appel récursif à la fin et tout fonctionnera comme il se doit. Avant l'appel récursif, l'unification avec la variable ab aura lieu et l'appel récursif sera effectué à partir de la fin de la liste donnée (comme une fonction récursive normale). Cette définition avec un appel récursif à la fin fonctionnera bien dans toutes les directions: à l'appel récursif, nous parvenons à accumuler toutes les informations possibles sur les arguments.

Cependant, dans tout exemple légèrement plus complexe, lorsqu'il y a plusieurs appels significatifs, un ordre spécifique pour lequel tout ira bien n'existe pas. L'exemple le plus simple: développer une liste en utilisant la concaténation. Nous corrigeons le premier argument - nous avons besoin de cet ordre particulier, nous corrigeons le second - nous devons échanger les appels. Sinon, la recherche est longue et la recherche ne s'arrête pas.

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr)) 

En effet, l'entrelacement des processus de recherche se conjugue de manière séquentielle, et personne ne pouvait penser à comment le faire différemment sans perdre une efficacité acceptable, bien qu'ils aient essayé. Bien sûr, toutes les solutions seront un jour trouvées, mais avec le mauvais ordre, elles seront recherchées de manière si irréaliste qu'il n'y a aucun sens pratique à cela.

Il existe des techniques pour écrire des programmes pour éviter ce problème. Mais beaucoup d'entre eux nécessitent des compétences et une imagination particulières pour être utilisés, et le résultat est de très gros programmes. Un exemple est le terme technique de délimitation de taille et la définition de la division binaire avec le reste par multiplication avec son aide. Au lieu d'écrire bêtement une définition mathématique

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm)) 

Je dois écrire une définition récursive de 20 lignes + une grande fonction auxiliaire qui n'est pas réaliste à lire (je ne comprends toujours pas ce qui se fait là-bas). Il peut être trouvé dans la dissertation de Will Bird dans la section Pure Binary Arithmetic.

Compte tenu de ce qui précède, je voudrais proposer une sorte de modification de la recherche afin que des programmes simples et écrits naturellement fonctionnent également.

Optimiser

Nous avons remarqué que lorsque tout va mal, la recherche ne se terminera que si vous indiquez explicitement le nombre de réponses et le cassez. Par conséquent, ils ont décidé de lutter précisément contre le caractère incomplet de la recherche - il est beaucoup plus facile à concrétiser que «ça marche depuis longtemps». En général, bien sûr, je veux juste accélérer la recherche, mais c'est beaucoup plus difficile à formaliser, alors nous avons commencé avec une tâche moins ambitieuse.

Dans la plupart des cas, lorsque la recherche diverge, une situation se produit qui est facile à suivre. Si une fonction est appelée récursivement, et dans un appel récursif, les arguments sont identiques ou moins spécifiques, puis dans l'appel récursif une autre de ces sous-tâches est à nouveau générée et une récursion infinie se produit. Formellement, cela ressemble à ceci: il y a une substitution, en appliquant laquelle aux nouveaux arguments, nous obtenons les anciens. Par exemple, dans la figure ci-dessous, un appel récursif est une généralisation de l'original: vous pouvez remplacer $$$c_2$= [x, 3], $$$d_2$= x et obtenez l'appel d'origine.



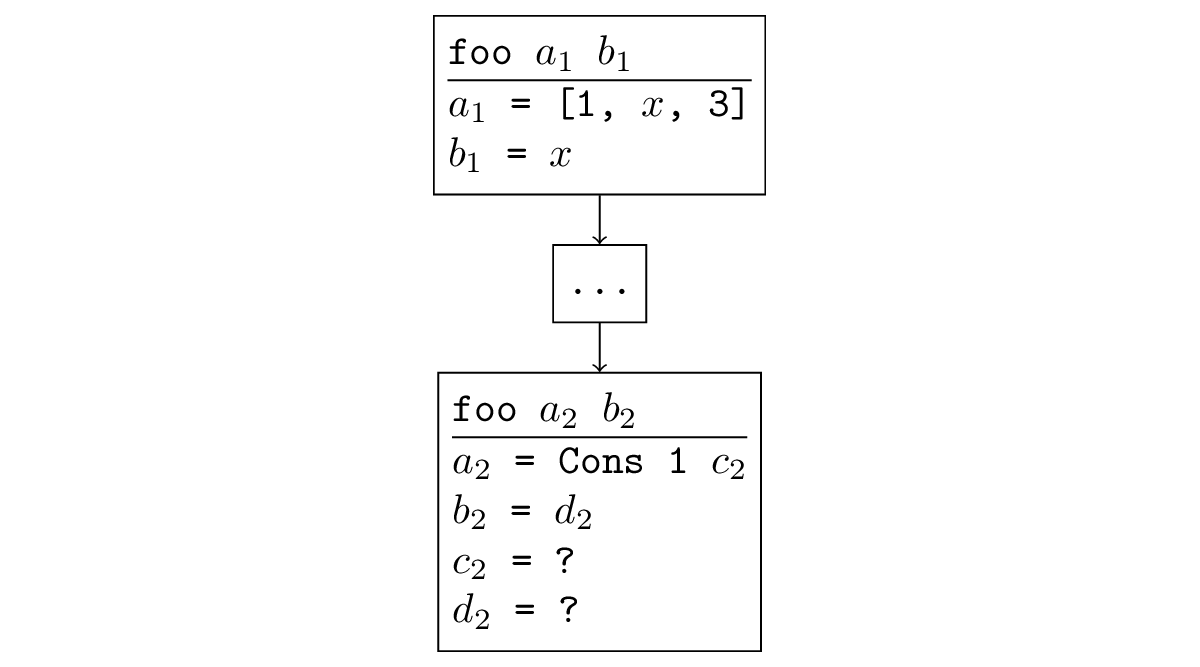
On peut constater que cette situation se produit également dans les exemples de divergence que nous avons déjà rencontrés. Comme je l'ai écrit plus tôt, lorsque vous exécutez appendo dans la direction opposée, un appel récursif sera effectué avec des variables libres au lieu de toutes les variables, ce qui, bien sûr, est moins spécifique que l'appel d'origine, dans lequel le troisième argument a été fixé.

Si nous exécutons reverso avec x =? et xr = [1, 2, 3], on peut voir que le premier appel récursif se produira à nouveau avec deux variables libres, donc de nouveaux arguments peuvent de nouveau être évidemment transférés aux précédents.

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *) 

En utilisant ce critère, nous pouvons détecter une divergence dans le processus d'exécution du programme, comprendre que tout va mal avec cet ordre et le changer dynamiquement en un autre. Grâce à cela, idéalement, la bonne commande sera sélectionnée pour chaque appel.
Vous pouvez le faire naïvement: si une divergence est trouvée dans le conjonctif, alors nous martelons toutes les réponses qu'il a déjà trouvées et reportons son exécution pour plus tard, «sautant en avant» le prochain conjonctif. Ensuite, peut-être, lorsque nous continuerons à l'exécuter, plus d'informations seront déjà connues et aucune divergence ne se produira. Dans nos exemples, cela conduira aux conjonctions de swap souhaitées.

Il existe des moyens moins naïfs qui permettent, par exemple, de ne pas perdre le travail déjà fait, de reporter la performance. Déjà avec la variante la plus stupide de changer l'ordre, la divergence a disparu dans tous les exemples simples souffrant de la non-commutativité de la conjonction, que nous connaissons, notamment:

• trier la liste des nombres (c'est aussi la génération de toutes les permutations de la liste),
  
• Arithmétique peano et arithmétique binaire,
  
• génération d'arbres binaires d'une taille donnée.
  

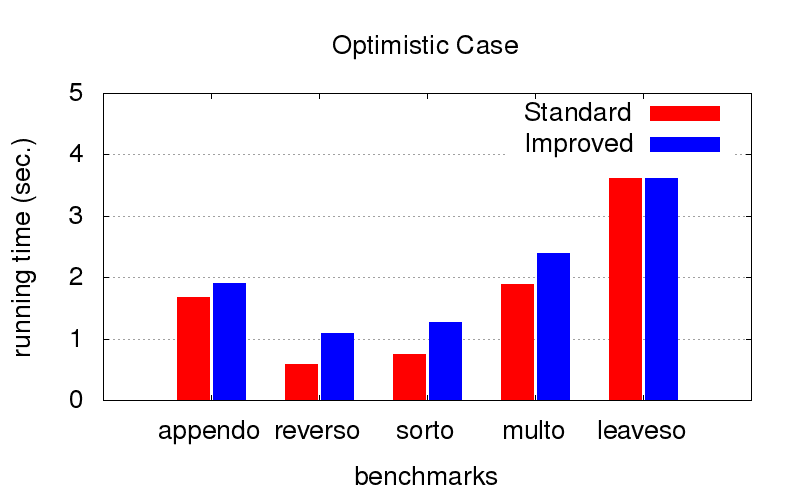
Ce fut une surprise inattendue pour nous. En plus de la divergence, l'optimisation lutte également contre les ralentissements de programme. Les diagrammes ci-dessous montrent le temps d'exécution de programmes avec deux ordres différents en conjonction (relativement parlant, l'un des meilleurs et l'un des nombreux mauvais). Il a été lancé sur un ordinateur avec la configuration du processeur Intel Core i7 M 620, 2,67 GHz x 4, 8 Go de RAM avec le système d'exploitation Ubuntu 16.04.

Lorsque l' ordre est déjà optimal (nous le sélectionnons à la main), l'optimisation ralentit un peu l'exécution, mais pas critique


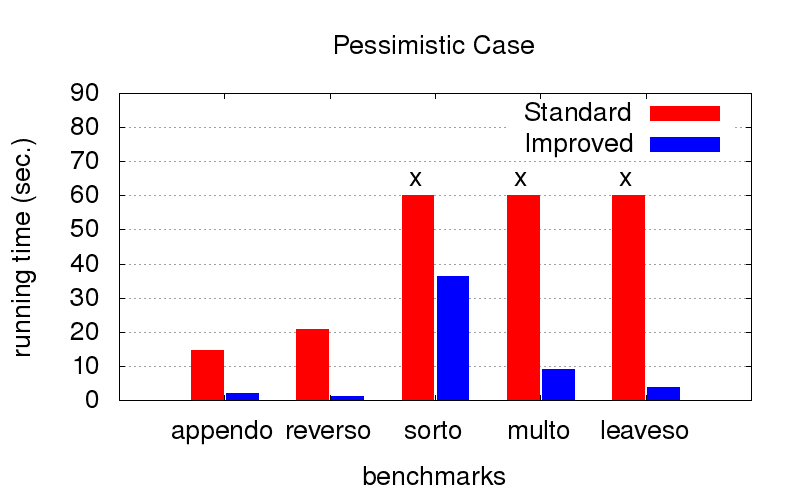
Mais lorsque la commande n'est pas optimale (par exemple, ne convient que pour un lancement dans la direction opposée), avec l'optimisation, cela se révèle beaucoup plus rapide. Les croix signifient que nous ne pouvions tout simplement pas attendre la fin, cela fonctionne beaucoup plus longtemps

Comment ne rien casser

Tout cela était basé uniquement sur l'intuition et nous voulions le prouver strictement. Théorie après tout.

Pour prouver quelque chose, nous avons besoin d'une sémantique formelle du langage. Nous avons décrit la sémantique opérationnelle pour miniKanren. Il s'agit d'une version simplifiée et mathématique d'une implémentation de langage réel. Il utilise une version très limitée (donc facile à utiliser), dans laquelle vous ne pouvez spécifier que l'exécution finale des programmes (la recherche doit être finale). Mais pour nos besoins, c'est exactement ce dont nous avons besoin.

Pour prouver le critère, le lemme est d'abord formulé: l'exécution du programme à partir d'un état plus général fonctionnera plus longtemps. Formellement: l'arborescence de sortie en sémantique a une grande hauteur. Cela est prouvé par induction, mais l'énoncé doit être très soigneusement généralisé, sinon l'hypothèse inductive ne sera pas assez forte. Il résulte de ce lemme que si un critère a fonctionné pendant l'exécution du programme, alors l'arbre de sortie a son propre sous-arbre de hauteur supérieure ou égale. Cela donne une contradiction, car pour une sémantique inductive, tous les arbres sont finis. Cela signifie que dans notre sémantique, l'exécution de ce programme est inexprimable, ce qui implique que sa recherche ne se termine pas.

La méthode proposée est conservatrice: nous ne changeons quelque chose que lorsque nous sommes convaincus que tout est déjà complètement mauvais et impossible de faire pire, donc nous ne cassons rien en termes d'achèvement du programme.

La preuve principale contient beaucoup de détails, nous avons donc voulu la vérifier formellement en écrivant à Coq . Cependant, cela s'est avéré assez difficile techniquement, nous avons donc calmé notre ardeur et nous nous sommes sérieusement engagés dans la vérification automatique uniquement dans la magistrature.

Publication

Au milieu du travail, nous avons présenté cette étude lors de la session d' affiches de l' ICFP-2017 au Concours de recherche des étudiants . Nous y avons rencontré les créateurs de la langue - Will Bird et Daniel Friedman - et ils ont dit qu'elle était significative et que nous devions la regarder plus en détail. Soit dit en passant, Will est généralement ami avec notre laboratoire de JetBrains Research. Toutes nos recherches sur miniKanren ont commencé quand, en 2015, Will a organisé une école d'été en programmation relationnelle à Saint-Pétersbourg.

Un an plus tard, nous avons amené notre travail sous une forme plus ou moins complète et présenté l' article aux Principes et pratiques de la programmation déclarative 2018.

Que dois-je faire à l'école d'études supérieures

Nous voulions continuer à nous engager dans une sémantique formelle pour miniKanren et une preuve rigoureuse de toutes ses propriétés. Dans la littérature, les propriétés (souvent loin d'être évidentes) sont simplement postulées et démontrées à l'aide d'exemples, mais personne ne prouve rien. Par exemple, le livre principal sur la programmation relationnelle est une liste de questions et réponses, chacune étant consacrée à un morceau de code spécifique. Même pour la déclaration d'intégralité de la recherche entrelacée (et c'est l'un des avantages les plus importants de miniKanren par rapport au Prolog standard), il est impossible de trouver une formulation stricte. Vous ne pouvez pas vivre comme ça, nous avons décidé, et, après avoir reçu une bénédiction de Will, nous nous sommes mis au travail.

Permettez-moi de vous rappeler que la sémantique que nous avons développée à l'étape précédente avait une limitation importante: seuls les programmes à recherche finie ont été décrits. Dans miniKanren, les programmes en cours d'exécution sont également intéressants car ils peuvent répertorier un nombre infini de réponses. Par conséquent, nous avions besoin d'une sémantique plus cool.

Il existe de nombreuses façons standard de définir la sémantique d'un langage de programmation, nous n'avons eu qu'à en choisir une et à l'adapter à un cas spécifique. Nous avons décrit la sémantique comme un système de transition étiqueté - un ensemble d'états possibles dans le processus de recherche et les transitions entre ces états, dont certains sont marqués, ce qui signifie qu'à ce stade de la recherche, une autre réponse a été trouvée. L'exécution d'un programme particulier est ainsi déterminée par la séquence de ces transitions. Ces séquences peuvent être finies (arriver à un état terminal) ou infinies, décrivant simultanément la fin et la fin de programmes. Afin de spécifier complètement un tel objet mathématiquement, il faut utiliser une définition coinductive.

— . , (, , — ..). , miniKanren' ( ).

, , — . . ( ), , .
( ): , , , .

, , / .

Coq'a. , , «. Qed». .