🌽 ☦️ 🤦🏻 Wolfensteiny 3D - reverse engineering 251 octets de JavaScript 🚒 🤼 👨‍✈️

Lors de l'écriture de code, beaucoup ne pensent à rien d'autre qu'à la logique du programme lui-même. Moins de gens pensent à optimiser le code au fil du temps, de la mémoire. Mais seuls quelques-uns atteignent le dernier niveau - compresser le programme à une taille record.

Regardez, par exemple, le résultat de seulement 251 octets de JavaScript:

Eh bien, découvrons comment cela fonctionne!

D'où vient-il?

Ce code, ainsi que beaucoup de ce vers quoi je me suis tourné dans cet article, est situé sur le site p01.org du magnifique Mathieu 'p01' Henri, développeur JavaScript et pas seulement souvent impliqué dans la compression du code à des tailles impossibles. Le matériel source de cet article est ici .

Donc, avant que vous soyez les 251 octets de code source.

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

Il est clair que rien n'est clair.

Rendre le code lisible

Tout d'abord, j'ai mis tout le code JavaScript dans une balise séparée, pour plus de commodité.

On peut voir que les variables E , h , Q , F et autres sont des constantes qui peuvent être remplacées par leurs valeurs / objets elles-mêmes, ainsi que changer les noms.

 var context = c.getContext("2d") var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,bd?4:D/2,D/2))for(D=0;'.'<F[D*y/hD/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1" var t = 75 var size = 75 function render(){ t += 0.2; c.height=300; for(let x = size; x--;) for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2)) for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 } setInterval(render, 75);

Ici, le code de la chaîne a déjà été extrait de la fonction, et la chaîne elle-même est intacte, nous en aurons besoin à l'avenir.

Convertissez maintenant les deux boucles externes en while .

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1 context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2); y--; } x--; } }

Comment voyons-nous cela?

Comprenons pourquoi nous le voyons du tout. Si vous regardez à nouveau l'image, vous pouvez comprendre beaucoup de choses.

Image cliquable

Voici ce que nous voyons:

Plus le sujet est éloigné, plus il est sombre
La partie oblique des obstacles rencontrés est inondée différemment de lignes et non de points.

Dans le code, le dessin se reflète comme ceci:

 // ,  ,       //   ||     // | | || | | // ↓ ↓ ↓↓ ↓ ↓ context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

Pourquoi voit-on des objets volumétriques dans ce flot de points noirs? Après tout, nous devons nous contenter de différentes nuances de noir - la taille des points noirs (nous ne pouvons pas changer la couleur, E.fillStyle est trop long!). En fait, cela fonctionne simplement parce que dans une image en deux dimensions, notre œil repose principalement sur l'ombre et la luminosité de la lumière.

Imaginez-vous marchant le long d'un couloir sombre avec seulement une lampe de poche dans vos mains. Vous brillez devant vous et voyez que certains objets sont plus proches et plus lumineux (une lampe de poche brille, un obstacle est brillant, il n'y a pas d'ombres), tandis que d'autres sont plus lointains et plus sombres (la lumière est dispersée, faible, et nous voyons l'obscurité - et nous sentons la distance). Donc ici - plus l'objet est éloigné ( D plus grand), plus la taille est grande, nous dessinons un carré noir sur l'écran.
Mais comment savoir ce qui doit être brillant et ce qui ne l'est pas?

Comptez le pixel

Maintenant, parlons de ce monstre:

 for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d) D += 0.1

Alors. Toute cette expression est un algorithme de raymarching à pas fixe qui vous permet de trouver l'intersection du faisceau avec les blocs. Pour chaque pixel de l'écran, nous lançons un faisceau, et nous le suivons avec un pas fixe de 0.1 , et dès que nous rencontrons un obstacle, nous terminons l'algorithme et dessinons un pixel sur l'écran, connaissant la distance à l'obstacle.

Commençons à lire ce code en plusieurs parties.

Condition D * y / size - D / 2 | 0 D * y / size - D / 2 | 0 peut être représenté par

D * (f r a c y t a i l l e - f r a c 12) = D * (f r a c y - t a i l l e / 2 t a i l l e) < 1

$D * (\ frac {y} {taille} - \ frac {1} {2}) = D * (\ frac {y - taille / 2} {taille}) <1$ , alors l'expression entre parenthèses montrera la «déviation» y rapport au centre de l'écran (en fractions de l'écran). Nous essayons donc de comprendre si le faisceau est entre le sol et le plafond ou non. Par conséquent, si nous touchons le sol (ou le plafond), nous sortons de la boucle plus loin, pour dessiner et dessiner un pixel.
Et si on ne touche pas, alors on continue les calculs: on cherche les coordonnées actuelles du faisceau.

 var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t)   //    var xcoord = t + depth * Math.cos(T); var ycoord = 3.5 + depth * Math.cos(T - 8); //

Pourquoi cos (T - 8)?

Il s'avère donc que

c o s (x - 8) a p p r o x s i n (x)

$cos (x-8) \ approx sin (x)$ avec une précision de 0,15 radians. Tout ça parce que

f r a c 5 p i 2 e n v i r o n 8, 15 e n v i r o n 8

$\ frac {5 \ pi} {2} \ environ 8,15 \ environ 8$

et puis

c o s (a l p h a - 8) a p p r o x c o s (a l p h a - f r a c 5 p i 2) = c o s (a l p h a - f r a c p i 2) = s i n (a l p h a)

$cos (\ alpha-8) \ approx cos (\ alpha- \ frac {5 \ pi} {2}) = cos (\ alpha - \ frac {\ pi} {2}) = sin (\ alpha)$

Il vaut la peine de parler de la façon dont un point dans l'espace est vérifié pour un bloc en général. La carte elle-même est extraite du code source ( F ) et ressemble à ceci:

 t+=.2,Q= ----> ░█░█░█░░ Math.cos ----> ░░░░█░░░ ;c.heigh ----> ░░█░░░░░   - t=300;fo ----> ░░░░░░░░ <----  , r(x=h;x- ----> ░█░░░░░█     -;)for(y ----> █░█░░░█░ =h;y--;E ----> ░░░░██░░ .fillRec ----> █░░░░░░░

Il semble donc en mouvement, le champ de vision de la caméra est indiqué ici.

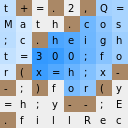
Les cellules dont le code de symbole est inférieur au code de point - "." Sont marquées en noir "." - c'est-à-dire les caractères !"#$%&'()*+,-. Maintenant nous arrondissons les coordonnées du faisceau, et essayons de savoir si la lettre dans ces" coordonnées "est sombre (un obstacle) ou pas (nous faisons voler le faisceau plus loin).

Étant donné que l'index est un et que les coordonnées sont deux, nous utilisons le hack:

 var boxIndex = xcoord & 7 | ycoord << 3;

En conséquence, nous obtenons un nombre qui reflète le numéro de bloc (enfin, ou vide).

Revenons au code. Maintenant, il a l'air décent.

Le code est un peu gras

 function render(){ t += 0.2; c.height=300; let x = size; while(x > 0){ let y = size; while(y > 0){ var depth = 0 while(depth < 8){ depth += 0.1 var T = x / size - .5 + Math.cos(t) / 8; //   var isFloorOrCeiling = depth * y / size - depth / 2 | 0; //      ? if(isFloorOrCeiling) break; var xcoord = t + depth * Math.cos(T) & 7; var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin boxIndex = xcoord | ycoord << 3; //     , //    if ('.' >= F[boxIndex]) break; b = xcoord; //  ?  ! } context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2) y--; } x--; } }

Retour au dessin

Pourquoi avions-nous besoin de tout cela? Maintenant, après avoir exécuté cet algorithme, nous connaissons la distance à l'objet et nous pouvons la dessiner. Mais une question est restée sans réponse: comment distinguer le plafond d'une unité séparée? Après tout, la distance au plafond et au bloc sont des nombres qui ne sont pas différents! En fait, nous avons déjà répondu à cette question.

 // ,  ,      // || // ↓↓ context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

Il y a une condition dans le code liée à la variable b , et affectant la largeur du "gros pixel noir": b - xcoord ? 4 : depth / 2 b - xcoord ? 4 : depth / 2 . Supprimons cette condition et voyons ce qui se passe sans:

Il n'y a pas de frontières entre les blocs et le plafond! (cliquable)

La condition b - xcoord nous donnera une largeur constante lorsque le changement de coordonnées est 0. Et quand cela ne peut-il pas se produire? Cela ne se produit pas uniquement lorsque nous n'atteignons pas la ligne (2) dans le code:

 // .... var xcoord = t + depth * Math.cos(T) & 7; // <---    (1) // ... if ('.' >= F[boxIndex]) // <---    (3) break; b = xcoord; // <---     (2) // ....

Cela signifie que le programme quitte le cycle plus tôt, sur la ligne (3) , lorsque le faisceau pénètre dans un bloc opaque dans la direction presque perpendiculaire à sa paroi, c'est-à-dire qu'il tombe dans la face "face" du bloc. Ainsi, tous les blocs sont différents du sol et du plafond.

Donc, c'est ainsi que cette belle image 3D se révèle, ce qui non seulement plaît à l'œil, mais vous fait également réfléchir à comment et pourquoi cela fonctionne. Vous pouvez voir ce code en action ici (off. Site du développeur de ce miracle).

Wolfensteiny 3D - reverse engineering 251 octets de JavaScript

Rendre le code lisible

Comment voyons-nous cela?

Comptez le pixel

Retour au dessin

More articles: