En 1974, le mathématicien britannique Roger Penrose a créé un ensemble révolutionnaire de carreaux qui peuvent être utilisés pour remplir un plan infini avec un motif qui ne se répète jamais. En 1982, le cristallographe israélien Daniel Shekhtman a découvert un alliage métallique dont les atomes étaient disposés dans un ordre jamais rencontré auparavant dans la science des matériaux. Penrose a obtenu une reconnaissance publique massive, rarement accordée aux mathématiciens. Shekhtman a reçu le prix Nobel. Les deux scientifiques ont contesté l'intuition humaine et changé les bases de la compréhension de la structure de la nature, constatant qu'une variabilité infinie peut se produire même dans un environnement hautement ordonné.
Au cœur de leurs découvertes se trouve une «symétrie interdite», appelée ainsi parce qu'elle contredit la connexion profondément enracinée entre la symétrie et la répétabilité. La symétrie est basée sur les axes de réflexion - tout ce qui se trouve d'un côté de la ligne est dupliqué de l'autre. En mathématiques, cette connexion est exprimée par des modèles d'espace de mosaïque. Les formes symétriques, telles que les rectangles et les triangles, peuvent remplir le plan sans lacunes ni superpositions, créant un motif répétitif constant. Les motifs répétitifs sont appelés «périodiques» et ils auraient une «symétrie de transfert». Si vous déplacez le motif (motif) d'un endroit à l'autre, il se ressemblera.
En tant que scientifique audacieux et ambitieux, Penrose n'était plus intéressé par les mêmes modèles et répétabilité, mais par une variabilité infinie. Plus précisément, il s'intéressait au carrelage «apériodique», c'est-à-dire aux ensembles de figures qui peuvent remplir un plan infini sans lacunes ni superpositions, et le motif de carrelage n'est jamais répété. C'était une tâche difficile car il ne pouvait pas utiliser des figures (tuiles) avec deux, trois, quatre ou six axes de symétrie - rectangles, triangles, carrés ou hexagones - parce que sur un plan infini, ils créeraient des motifs périodiques ou répétitifs. Autrement dit, il avait besoin d'utiliser des figures qui étaient censées laisser des lacunes lors du remplissage de l'avion - des figures qui ont interdit la symétrie.
Pour créer son propre plan de motifs non répétitifs, Penrose s'est tourné vers la symétrie à cinq axes - vers les pentagones, en particulier parce que, selon lui, il est «tout simplement agréable de regarder les pentagones». La chose remarquable au sujet des figures de Penrose était que bien qu'il ait obtenu ces chiffres des lignes et des coins des rectangles, ils ne laissaient pas de vides trous. Ils s'ajustent étroitement l'un contre l'autre, se pliant et tournant sur l'avion, étant toujours proches de la répétabilité, mais ne l'atteignant jamais.
La mosaïque de Penrose a attiré l'attention du public pour deux raisons principales. Tout d'abord, il a trouvé un moyen de générer des motifs changeant à l'infini à partir de seulement deux types de formes. Deuxièmement, ses carreaux étaient des figures simples et symétriques, qui en elles-mêmes ne présentaient aucun signe de propriétés inhabituelles.

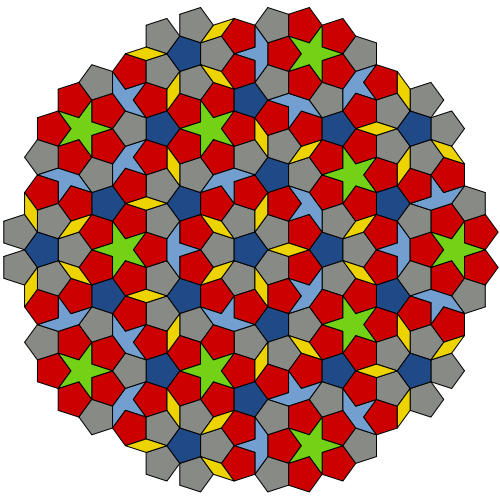
Penrose a créé plusieurs variétés de ses ensembles apériodiques de figures. L'un des plus célèbres s'appelle «serpent» et «fléchette». Le «cerf-volant» ressemble à un cerf-volant pour enfants et le «fléchette» ressemble à la silhouette simplifiée d'un bombardier furtif. Les deux sont clairement divisés le long des axes de symétrie et chacun d'eux a de simples arcs symétriques à la surface. Penrose a défini une règle pour le placement des formes: pour le placement "correct" des tuiles, ces arcs doivent correspondre, créant des courbes inextricables. Sans cette règle, les «serpents» et les «fléchettes» peuvent être organisés en motifs répétitifs. Si vous suivez cette règle, la répétition ne se produit jamais. «Serpent» et «fléchette» remplissent infiniment l'avion, dansant autour de leurs cinq axes, créant des étoiles et des décagones, courbant des courbes, des papillons et des fleurs. Les chiffres se répètent, mais de nouvelles variations y apparaissent.
Le professeur clinicien de mathématiques Edmund Harriss de l'Université de l'Arkansas, qui a écrit un doctorat sur les carreaux de Penrose, propose une telle comparaison. «Imaginez que vous vivez dans un monde de carrés. Vous commencez à marcher et lorsque vous arrivez au bout de la place, la suivante est exactement la même, et vous savez ce que vous verrez si vous continuez à bouger sans fin. " Les carreaux de Penrose ont exactement la nature opposée. «Quelles que soient les informations dont vous disposez, quelle que soit la partie du schéma que vous voyez, vous ne pouvez jamais prédire ce qui va se passer ensuite. Il y aura toujours quelque chose que vous n'avez jamais vu auparavant. »
L'un des aspects curieux de la division apériodique d'un avion est que les informations de positionnement sont en quelque sorte transmises sur de longues distances - la tuile Penrose, posée au même endroit, interfère avec le placement d'autres tuiles dans les centaines (et aussi des milliers et des millions) de tuiles. «Une contrainte locale crée en quelque sorte une contrainte globale», explique Harriss. "Cela suggère qu'à aucune échelle ces carreaux ne créeront quelque chose de périodique." Vous pouvez avoir le choix de placer, disons, un «serpent» dans une zone, ou une «fléchette» dans un endroit éloigné. N'importe laquelle des tuiles fera l'affaire, mais pas les deux.
Ces tuiles, formant un motif sans fin et non répétitif, expriment le rapport de Fibonacci, également connu sous le nom de "nombre d'or". On dit que deux nombres ont un nombre d'or si le rapport d'un plus petit nombre à un plus grand est le même que le rapport d'un plus grand nombre à la somme de deux nombres. Dans ce cas, le rapport de l'aire du "serpent" à l'aire de la "fléchette" est le nombre d'or. Le rapport du côté long du "serpent" à son côté court est également le nombre d'or.
Les carreaux Penrose peuvent également être subdivisés en versions plus petites d'eux-mêmes. Un «serpent» se compose de deux «serpents» plus petits et de deux moitiés de «fléchettes». La «fléchette» se compose d'un petit «serpent» et de deux tapis «fléchettes». (Dans toute mosaïque appropriée de Penrose, ces moitiés des «fléchettes» sont alignées les unes avec les autres. Du point de vue des mathématiques, cela leur permet d'être considérées comme des «fléchettes» entières.) "" Dit Harriss. «Si je les subdivise, j'obtiendrai 2« serpents »
A +
B et « fléchettes »
A +
B.Si vous effectuez cette substitution un nombre infini de fois, vous pouvez calculer la part totale de chaque type de tuile, comme si elle était disposée sur un plan infini. Dans de tels calculs, un motif
répétitif conduit toujours à un nombre rationnel. Si la proportion est un nombre irrationnel, cela signifie que le motif ne se répétera jamais réellement. Dans les calculs des tuiles de Penrose, non seulement le nombre irrationnel est obtenu, leur rapport est le rapport de Fibonacci - le rapport des "fléchettes" aux "serpents" est égal au rapport des "serpents" au nombre total de tuiles.
Étant donné que la proportion de Fibonacci est omniprésente dans la nature - des ananas aux populations de lapins - il est encore plus étrange que cette proportion soit fondamentale pour le système de carrelage, qui, semble-t-il, n'a rien à voir avec le monde physique. Penrose a créé quelque chose de nouveau dans la science, intriguant précisément là qu'il ne devrait pas fonctionner comme le fait la nature. C'était comme si Penrose avait écrit une histoire de science-fiction sur une nouvelle espèce animale, puis le zoologiste a découvert cette espèce vivant sur Terre. En fait, les carreaux Penrose sont associés au nombre d'or, aux mathématiques que nous avons inventées et aux mathématiques du monde qui nous entoure.

Reprenant l'étude de la symétrie interdite, Penrose ne pouvait pas deviner qu'il était devenu partie intégrante du changement de pensée qui avait conduit à la découverte d'un nouveau domaine de la science mathématique. Après tout, la symétrie est fondamentale à la fois pour les mathématiques pures et le monde naturel. L'astrophysicien Mario Livio a qualifié la symétrie de "l'un des outils les plus nécessaires pour déchiffrer la structure de la nature". La nature utilise des carrés et des hexagones pour la même raison que les humains: ils sont simples, efficaces et ordonnés. Si les pentagones semblaient peu pratiques, même pour une tâche aussi simple que le remplissage de carreaux de sol dans la décoration intérieure, alors, bien sûr, on pensait qu'ils ne pouvaient pas être utilisés pour créer des atomes dans des matériaux solides comme les cristaux.
Les cristaux sont constitués de réseaux tridimensionnels d'atomes. Les cristaux se développent en ajoutant de nouveaux atomes et en élargissant les réseaux. Cela se produit plus efficacement lorsque les atomes s'alignent en motifs répétitifs. Pendant des décennies, l'histoire s'est arrêtée là: les cristaux répétaient des structures. Le point.
Mais ensuite, en 1982, Shekhtman a pris un congé créatif de l'Université Technion à Haïfa et a commencé à travailler au National Bureau of Standards. Il a tâtonné dans un laboratoire d'alliage aluminium-manganèse. Les motifs de diffraction créés par ses structures cristallines ne semblaient ressembler à aucune des symétries standard connues des cristallographes. En fait, les atomes se sont alignés dans les pentagones, les losanges, les «serpents» et les «fléchettes» que Penrose a découverts dans le monde des mathématiques.
«Bien sûr, je connaissais les carreaux Penrose», explique Schechtman. Mais il n'avait aucune raison de soupçonner leur lien avec cet alliage. «Je n'ai pas compris ce que c'est. Au cours des mois suivants, j'ai répété mes expériences encore et encore. À la fin de mes vacances créatives, je savais exactement ce que ce n'était pas, mais je n'avais toujours aucune idée de ce que c'était. »
Pour comprendre ce qu'il a découvert, Schechtman, comme Penrose, a dû remettre en question ses idées intuitives habituelles. Il a dû accepter la symétrie interdite et sa confusion pentagonale avec un manque de répétabilité. Pendant son séjour en Israël, il hésitait à reconnaître qu'il avait découvert une structure atomique cristalline non répétitive. Cependant, personne dans le monde de la science des matériaux ne pouvait au départ attribuer cette découverte aux cristaux. Par conséquent, ils ont été appelés «quasi-cristaux».
Les mathématiques bizarres de Penrose semblaient avoir éclaté dans le monde naturel. «Depuis 80 ans, les cristaux ont été définis comme des structures« ordonnées et périodiques », car tous les cristaux que nous avons étudiés depuis 1912 étaient périodiques», explique Schechtman. «Ce n'est qu'en 1992 que l'Union internationale des cristallographes a organisé un comité pour sélectionner une nouvelle définition du mot cristal. Cette nouvelle définition est un changement de paradigme pour la cristallographie. »
Ce n’est pas seulement la simple inertie de la pensée qui a empêché Shekhtman de comprendre et d’accepter la découverte. Les structures cristallines apériodiques n'étaient pas seulement inconnues - elles étaient considérées comme non naturelles. Rappelez-vous que l'emplacement d'une tuile Penrose peut affecter les formes de milliers de tuiles - les restrictions locales en créent des globales. Mais si un cristal est formé atome par atome, alors il ne devrait pas y avoir de loi de la nature qui crée les restrictions inhérentes aux carreaux de Penrose.
Il s'est avéré que les cristaux ne forment pas toujours atome par atome. «Dans les composés intermétalliques très complexes, les éléments sont énormes. Ils ne sont pas locaux », explique Schechtman. Lorsque de gros fragments de cristal se forment en même temps, plutôt que par la croissance progressive des atomes, les atomes situés très loin les uns des autres peuvent influencer la position mutuelle, tout comme dans les carreaux de Penrose.
Comme c'est le cas avec de nombreux tabous, la symétrie interdite a été reconnue comme l'une des formes d'existence acceptables dans la nature. Les quasi-cristaux ne sont pas seulement devenus un objet d'étude dans un nouveau domaine de recherche scientifique: il s'est avéré qu'ils ont de nombreuses propriétés utiles qui découlent de leur structure inhabituelle. Par exemple, leur configuration asymétrique d'atomes leur fournit une faible énergie de surface, c'est-à-dire que peu de choses peuvent s'y coller. Ainsi, les revêtements quasi-cristallins ont commencé à être utilisés dans les ustensiles de cuisine antiadhésifs. (Lorsque Penrose a créé ses nouvelles tuiles, il ne pouvait pas imaginer qu'elles seraient utilisées en cristallographie, sans parler de la friture des œufs.) De plus, les quasi-cristaux ont généralement un faible frottement et une faible usure, ce sont donc des revêtements idéaux pour les rasoirs et les chirurgiens. instruments ou tout autre instrument tranchant se rapportant au corps humain.

Étant donné que les structures quasi-cristallines ne sont jamais répétées, elles créent des modèles de diffraction uniques de rayonnement électromagnétique. Les chercheurs en photonique s'intéressent à la façon dont ils affectent la transmission de la lumière, la réflectivité et la photoluminescence. S'ils sont refroidis, leur résistance électrique chute à un niveau presque nul. Mais ils absorbent également le rayonnement infrarouge, de sorte qu'ils se réchauffent très rapidement à des températures élevées. De ce fait, ils s'avèrent être un ajout très utile aux imprimantes 3D, dans lesquelles la poudre plastique est utilisée comme matériau de départ. Shekhtman explique: si une poudre quasi-périodique est mélangée avec elle et exposée à un rayonnement infrarouge, alors la poudre quasi-périodique "s'échauffe extrêmement rapidement et fait fondre les particules de plastique environnantes, ce qui les fait coller ensemble."
Personne ne sait comment se termine l'histoire de la symétrie interdite. Les mathématiciens continuent d'explorer les propriétés des carreaux Penrose. Les quasi-cristaux restent le sujet d'étude en recherche fondamentale et appliquée. Mais jusqu'à présent, ce voyage a été incroyable. Au cours des 40 dernières années, la symétrie à cinq axes est passée de l'impraticable au précieux, du non naturel au complètement naturel, de l'interdit au dominant. Et pour cette transformation, il faut remercier deux scientifiques qui ont abandonné leurs idées habituelles pour découvrir une nouvelle forme remarquable de variations infinies de la nature.
À propos de l'auteur: Patchen Bars est un journaliste et auteur basé à Toronto. Il travaille actuellement sur un livre sur la relation entre les mathématiques pures et le monde naturel.