Fractales en nombre irrationnel

Cet article fait suite à mon premier article , Fractals in Prime Numbers .

Article suivant: Fractales en nombres irrationnels. 2e partie



Dans un article précédent, nous avons appris à dessiner des modèles auto-similaires à l'aide de nombres premiers mutuellement. Dans cet article, je montrerai la nature fractale du nombre $$$\ sqrt {2}$.
Sans préface. Sous le chat.

Nous définirons la terminologie et la notation. En mathématiques, les systèmes décrits ci-dessous sont appelés billards . De plus, nous utiliserons ce terme. Les dimensions du billard rectangulaire seront indiquées par $$$M$(largeur) et $$$N$(hauteur).

Billard binaire

Dans l'article précédent, nous avons pris un billard rectangulaire avec des côtés $$$M$et $$$N$, a lancé une balle dedans et a marqué la trajectoire avec une ligne pointillée à travers la cellule:



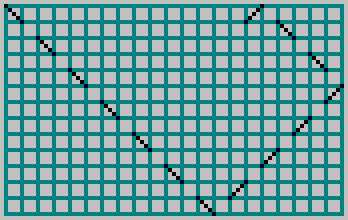
Pour mutuellement simple $$$M$et $$$N$nous obtenons le motif:



Dans la version binaire, nous marquons la trajectoire non pas avec une ligne pointillée, mais en peignant alternativement les cellules en noir et blanc (nous formons un tableau binaire, mettons 0 pour le noir et 1 pour le blanc dans la cellule correspondante):



Règles de réflexion des frontières:



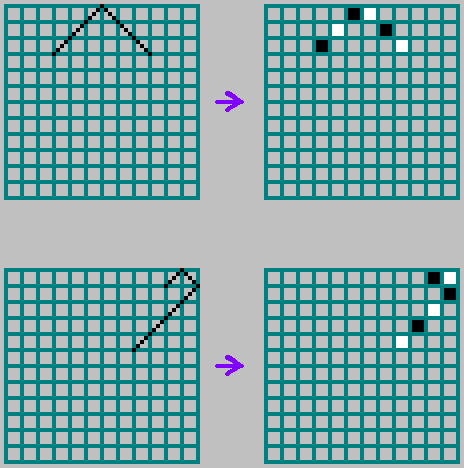
Pour mutuellement simple $$$M$et $$$N$la trajectoire traverse chaque cellule:




Si les parties ont un diviseur commun, la balle entre dans le coin avant de passer à travers chaque cellule:



Il est commode de considérer ce cas comme un billard dans un rectangle avec des côtés $$$\ frac {M} {GCD}$et $$$\ frac {N} {GCD}$(GCD est le plus grand facteur commun):



Avant de continuer, remplissez le tableau proposé par l'utilisateur Captain1312 dans son article (nous diviserons les côtés du billard en GCD).

$$$(1, 0)$un peu

Pour chaque table de billard $$$M$et $$$N$prendre un peu de coordonnées $$$(1, 0)$.



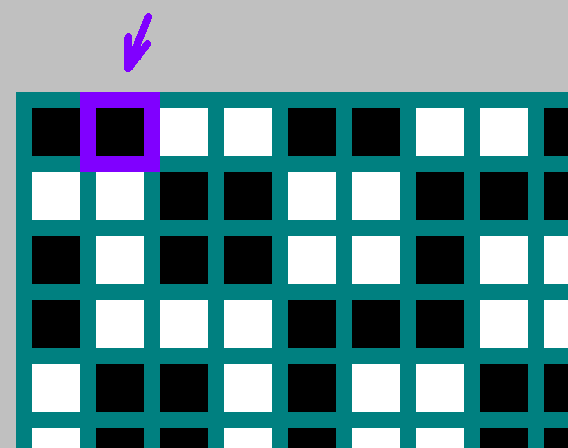
Si $$$M$est un diviseur $$$N$- puis un peu avec les coordonnées $$$(1, 0)$manquant ( $$$\ frac {M} {GCD} = 1$) Dans ce cas, nous prenons le bit inversé avec les coordonnées $$$(0, 1)$.

Remplissez le tableau. L'origine est le coin supérieur gauche. Par $$$x$- largeur de billard $$$M$par $$$y$- hauteur $$$N$. Pour chaque billard nous marquons un peu $$$(1, 0)$, ou bit inversé $$$(0, 1)$(nous reviendrons sur ce sujet ci-dessous).

Séquence binaire

Pourquoi avons-nous inversé le bit lorsque la largeur du billard $$$M = 1$? Pour mutuellement simple $$$M$et $$$N$, la trajectoire de la balle traverse chaque cellule. Entre les parois supérieure et gauche du billard, la balle passe à chaque fois un nombre pair de cellules.





Les bits de la colonne de gauche sont les bits inversés de la ligne supérieure. Nous ne prenons pas le bit zéro - la trajectoire commence avec:



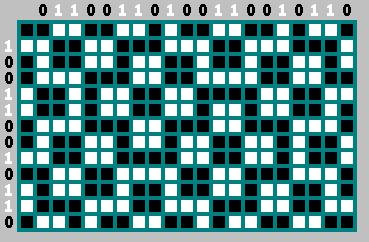
De plus, nous pouvons jeter en toute sécurité chaque deuxième bit de cette séquence (bit $$$2_ {n-1}$- bit inversé $$$2_ {n}$):



Vous avez la séquence $$ pour billard $$$(21,13)$. La séquence est unique à tout le monde. $$$M$et $$$N$.

Quelle que soit la hauteur $$$N$nous ne l'avons pas pris - le ballon suit toujours la trajectoire $$$2N$entre deux reflets de la paroi supérieure. Depuis la paroi supérieure, le mouvement commence toujours par un bit "0" (cellule noire) et se termine par un bit "1" (cellule blanche):



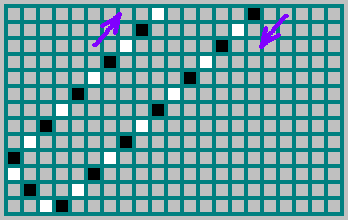
En fait, la séquence (que nous avons souligné ci-dessus - $$ ) indique de quel côté la balle est entrée: 1 - si la balle est entrée, réfléchie par le mur de droite et 0 - si la balle est entrée, réfléchie par le mur de gauche. Dans l'image, la trajectoire de la balle est marquée en noir si la balle s'est déplacée vers la droite et en blanc si elle s'est déplacée vers la gauche:




Cette séquence ( $$ ) contient toutes les informations nécessaires sur le modèle. Avec lui, nous pouvons restaurer le motif d'origine (et même regarder au-delà de la bordure inférieure du motif). Prenez un carré avec des côtés $$$M$. Nous organisons les morceaux de notre séquence aux endroits où la balle a frappé la paroi supérieure (la distance entre les touches adjacentes de la balle est de 2 cellules).



Si le bit correspondant = 1 - nous commençons à nous déplacer vers la gauche, marquant la trajectoire à travers la cellule. Si bit = 0 - déplacez-vous vers la droite.



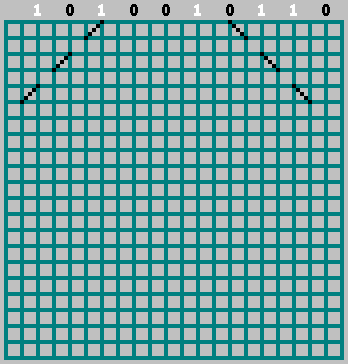
Dans ce cas, n'oubliez pas le bit zéro:



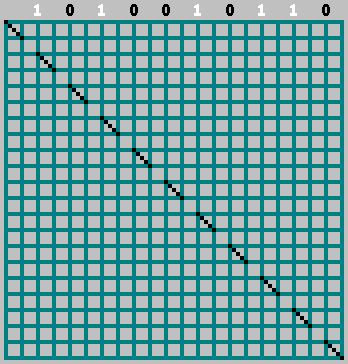
Gif:



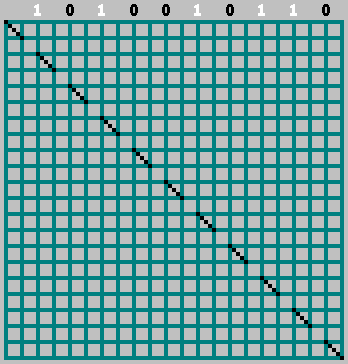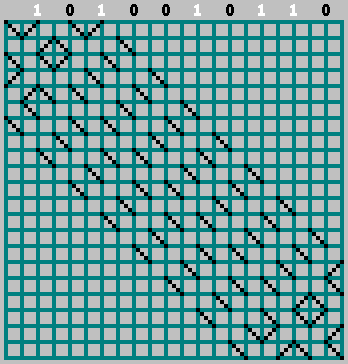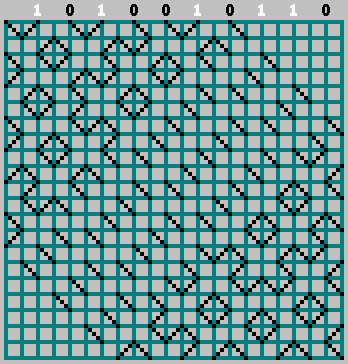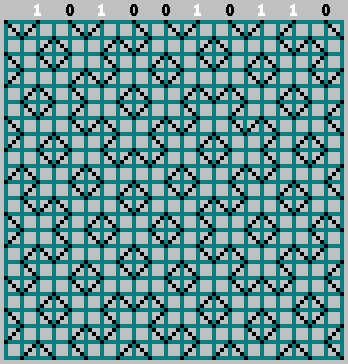
Nous avons obtenu le motif d'origine (et regardé un peu au-delà de la bordure inférieure):



Script pour visualiser des séquences binaires

Nous pouvons construire cette séquence en utilisant le reste de la division.

Billard unidimensionnel

Sur l'axe numérique $$$X$prendre deux points: $$$0$et $$$M$.



Passer d'un point à un autre, mesurer la distance $$$N$:



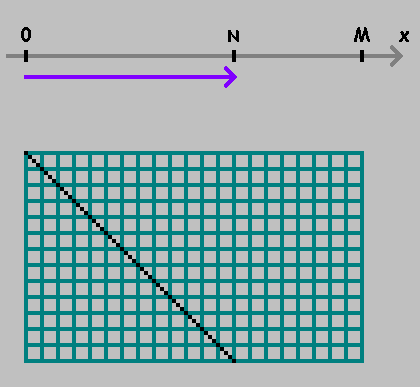
A marqué le point. Nous continuons à mesurer la distance de ce point, en gardant la direction. Si vous avez atteint le point $$$0$ou $$$M$- changer de direction:



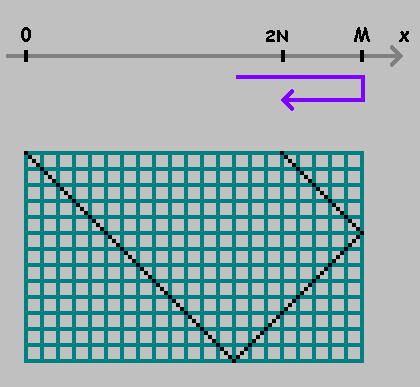
Comme on peut le voir sur les figures ci-dessus, le premier point montre l'endroit où la balle touche la paroi inférieure du billard. Ce point ne nous intéresse pas. Nous ne fixerons que des points $$$2kN$pour $$$k = 0,1,2, ...$.

Comment marquer ces points? Tournez nos billards sur l'axe $$$X$. Marquez les points $$ . Atteignant maintenant le point $$$M$nous ne changeons pas la direction du mouvement, mais continuons d'avancer au point $$ .



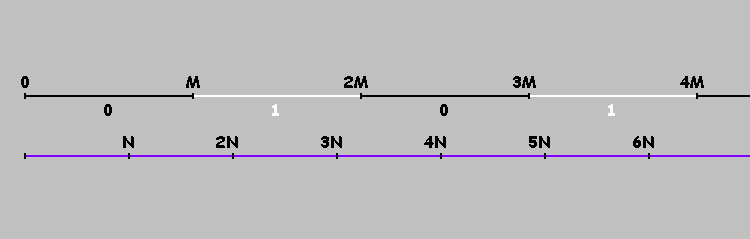
Multiples $$$M$, divisons notre axe en segments. Nous marquons conditionnellement ces segments avec des uns et des zéros (en alternance). Sur les segments marqués de zéros, la balle (dans un billard rectangulaire) se déplace de gauche à droite. Sur les segments marqués d'unités - de droite à gauche. Ou plus simple: la balle se déplace de gauche à droite si $$$Q_k = 0$pour

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

(Une attention particulière doit être portée à cette formule. Ensuite, nous y reviendrons)

Il est facile de voir que le point auquel la balle a touché la paroi supérieure du billard est le reste de la division $$$2kN$sur $$$M$. Dans ce cas, on ne peut pas fixer le mouvement du ballon dans la direction opposée. Nous prenons toute la partie de la division $$$2kN$sur $$$M$s'il est pair - nous considérons le reste de la division $$$2kN$sur $$$M$. Divisez le reste résultant par 2 (la distance entre les points de contact adjacents est de deux cellules). Vous avez les indices des éléments du tableau, que nous devons remplir de zéros. Les éléments restants sont remplis d'unités (la balle s'est déplacée du mur de droite vers la gauche).

Longueur de séquence = $$$\ frac {M} {2}$.

function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001 

Maintenant, nous pouvons construire une séquence binaire pour les billards avec tous les côtés $$$M$et $$$N$(en nombres naturels).
Quelques exemples:
144x89 (numéros de Fibonacci):
010100101101001011010110100101101001010010110100101101011010010110100101

169x70 (numéros Pell):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233x55 (nombres de Fibonacci impairs $$$F_n$et $$$F_ {n-3}$):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100


Nous avons des séquences. Sinon, comment pouvez-vous visualiser des séquences binaires? Utilisation de Turtle Graphics .

Graphiques de tortue

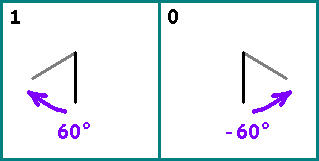
Tracez une ligne. Ensuite, nous prenons alternativement les bits de notre séquence. Si bit = 1 - tourner le segment par rapport au précédent $$ (dans le sens des aiguilles d'une montre). Si bit = 0 - tournez le segment de $$$-60 ^ {\ circ}$. Le début du segment suivant est la fin du précédent.



Prenez deux nombres de Fibonacci assez grands: $$$F_ {29} = 514229$et $$$F_ {28} = 317811$.

Construit la séquence:
00101101001011010010100101101001011010110100101101001010010110100101 ... (257114 caractères plus zéro bit).

Nous visualisons en utilisant des graphiques de tortues. La taille du segment initial est de 10 pixels (le segment initial dans le coin inférieur droit):



La taille du segment initial est de 5 pixels:



La taille du segment initial est de 1 pixel:



L'exemple suivant est les nombres Pell.

$$

$$P_n = \ begin {cases} 0, n = 0; \\ 1, n = 1 \\ 2P_ {n-1} + P_ {n-2}, n> 1 \ end {cases}$$

Prenez $$$P_ {16} = 470832$et $$$P_ {15} = 195025$.

Séquence:
0010100101011010100101011010100101001010110101001010110101000010101101 (235415 caractères plus zéro bit).

La taille du segment initial est de 1 pixel:



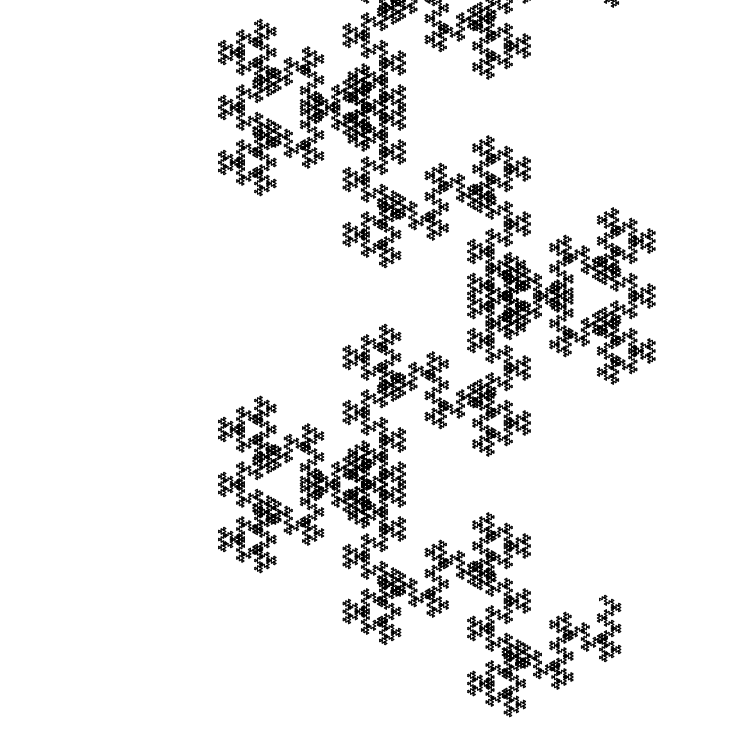
Un autre exemple est le nombre impair de Fibonacci $$$F_n$et $$$F_ {n-3}$.
Prenez $$$F_ {28} = 317811$et $$$F_ {25} = 75025$.
Séquence:
00110110010010011111001001001001101101100100110110110010010011011011001001 ... (158905 plus zéro bit).
Au lieu de coins $$ et $$$-60 ^ {\ circ}$nous utiliserons les coins $$ et $$$-90 ^ {\ circ}$.
La taille du segment initial est de 5 pixels:



La taille du segment initial est de 0,4 pixels:



Cette courbe a un nom - « fractal de mot de Fibonacci ». La dimension de Hausdorff pour cette courbe est connue:

$$

$$D = 3 {\ frac {\ log \ Phi} {\ log (1 + {\ sqrt {2}})}} = 1,6379; \ quad \ Phi = \ frac {1 + {\ sqrt {5}}} {2}$$

Script pour visualiser des séquences binaires à l'aide de Turtle Graphics

Le problème

Est-il possible de dessiner un motif pour le billard, dont les côtés sont incommensurables (l'un des côtés est un nombre irrationnel)? La tâche n'est pas anodine. En essayant de résoudre ce problème, nous serons confrontés à un certain nombre de questions:

1. Si les parties sont incommensurables - nous ne pouvons pas paver le billard avec des cellules de même taille.
2. Si les côtés sont incommensurables - la balle sera réfléchie à l'infini et ne frappera jamais le coin.
3. Les séquences de billard ne sont pas remplies dans l'ordre, mais au hasard.



Les deux premières questions n'ont évidemment pas de solution. Mais s'il y avait un moyen de remplir la séquence dans l'ordre, alors nous pourrions, en déplaçant la séquence de gauche à droite, restaurer le modèle de la manière que nous avons utilisée ci-dessus. Et ainsi voir à quoi ressemble le motif dans le coin supérieur gauche du billard, dont les côtés sont incommensurables.

Magie noire

Prenez le billard, dont les côtés sont égaux aux numéros de Fibonacci (avec d'autres numéros, une telle astuce peut ne pas fonctionner). Exécutez la balle dedans et fixez le numéro de la balle touchant la paroi supérieure. Remplissez les chiffres en blanc - si la balle s'est déplacée de droite à gauche et en noir - si la balle s'est déplacée de gauche à droite:



La couleur blanche correspond à un dans la séquence, noir - zéro. Maintenant, organisons les numéros dans l'ordre:



Nous avons obtenu exactement la même séquence de uns et de zéros.


En fait, dans certains cas, nous n'avons pas besoin de prendre le reste de la division. Pour les nombres de Fibonacci, il suffit de vérifier la parité de la partie entière de la division $$$2kN$sur $$$M$:

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Au numérateur nous avons $$$F_ {n}$. Au dénominateur - $$$F_ {n + 1}$.

Comme vous le savez:

$$

$$\ lim_ {n \ to \ infty} \ frac {F_n} {F_ {n + 1}} = \ frac {1} {\ Phi}$$

$$$\ Phi$- Le nombre d'or. Numéro irrationnel. Maintenant, nous pouvons écrire notre formule comme suit:

$$

$$Q_k = \ lfloor \ frac {2k} {\ Phi} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Nous avons obtenu une formule avec laquelle nous pouvons remplir la séquence pour le billard dans l'ordre, dont la largeur est égale à $$$\ Phi$et hauteur $$$1$. Longueur de séquence = $$$\ infty$, mais nous pouvons restaurer une partie du motif, en se déplaçant de gauche à droite en séquence et regarder dans le coin supérieur gauche du billard. Reste à savoir comment compter $$$\ Phi$

L'unité divisée par le nombre d'or peut être réécrite comme suit:

$$

$$\ frac {1} {\ Phi} = \ frac {-1 + {\ sqrt {5}}} {2}$$

On peut se débarrasser de deux:

$$

$$\ frac {2k} {\ Phi} = \ frac {2k (-1 + {\ sqrt {5}})} {2} = k \ sqrt {5} -k$$

Notre formule se présente sous la forme:

$$

$$Q_k = \ lfloor k \ sqrt {5} -k \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Pour plus de clarté, j'ai dessiné un tableau. Dans la troisième colonne, nous jetons la partie fractionnaire et laissons le tout. Dans la quatrième colonne, nous vérifions la parité de la partie entière:



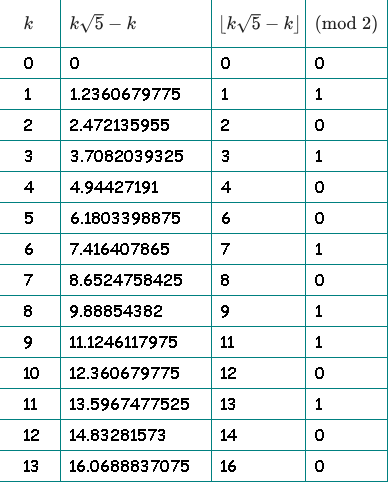
Dans la quatrième colonne, nous avons notre séquence: 01010010110100 ...

Nous continuons à calculer les bits pour le reste $$$k$. Restauration d'une partie du motif de billard avec des côtés $$$1$et $$$\ Phi$:



Si vous n'enlevez pas à chaque fois $$$k$- puis tous les deux bits de la séquence sont inversés. Nous obtenons la formule générale:

$$

$$Q_k = \ lfloor k \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

Qu'est-ce qui nous empêche d'utiliser la racine carrée de trois ou, disons, de deux au lieu de la racine carrée de cinq? Rien.

Nous construisons une séquence pour $$$k \ sqrt {3} + k$

 var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2; 

Les premiers bits de la séquence:
00100101101001001011010010110110100101101001001011010010010110100101 ...

Nous allons visualiser en utilisant des graphiques de tortues. Angles de 90 et -90 degrés. La taille initiale du segment est de 5 pixels:



La taille du segment initial est de 0,5 pixels:



Nous construisons une séquence pour $$$k \ sqrt {2}$

 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2; 

Les premiers bits de la séquence ( A083035 ):
01001101100100110010011011001101100100110110011011001001100100110110 ...

Angles de 90 et -90 degrés. La taille initiale du segment est de 5 pixels:



La taille du segment initial est de 0,5 pixels:





Angles de 60 et -60 degrés. La taille initiale du segment est de 5 pixels:



Script de visualisation

Quelqu'un peut douter que la parité de la partie entière de $$$k \ sqrt {2}$donne une séquence fractale. Nous visualisons une partie de cette séquence de la seconde manière:



Pour plus de clarté, j'ai peint sur la plus longue courbe du motif résultant:



Cette courbe a un nom - «fractal de mot de Fibonacci».

Comment obtenir cette séquence en utilisant le billard? Nous prenons des billards, dont la largeur = 1, et la hauteur = $$$\ sqrt {2}$. Aux limites supérieure et inférieure, nous fixons la direction du mouvement de la balle. Si la balle s'est déplacée de gauche à droite - écrire 0, si de droite à gauche - écrire 1.



Deux graphiques:

$$

$$z = \ lfloor y \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2)$$

$$

$$z = \ lfloor yx \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2)$$

Vous pouvez continuer dans cette veine pendant très longtemps - les motifs ont de nombreuses propriétés intéressantes. Mais l'article était déjà trop lourd. Je vais vous parler d'une des propriétés intéressantes à la fin.