
Lors du développement de
meshoptimizer , la question se pose souvent: "Cet algorithme peut-il utiliser SIMD?"
La bibliothèque est axée sur les performances, mais SIMD n'offre pas toujours des avantages de vitesse importants. Malheureusement, SIMD peut rendre le code moins portable et moins maintenable. Par conséquent, dans chaque cas, il est nécessaire de rechercher un compromis. Lorsque les performances sont primordiales, vous devez développer et maintenir des implémentations SIMD distinctes pour les jeux d'instructions SSE et NEON. Dans d'autres cas, vous devez comprendre quel est l'effet de l'utilisation de SIMD. Aujourd'hui, nous allons essayer d'accélérer le simplificateur de maillage bâclé - un nouvel algorithme récemment ajouté à la bibliothèque - en utilisant les jeux d'instructions SSEn / AVXn.
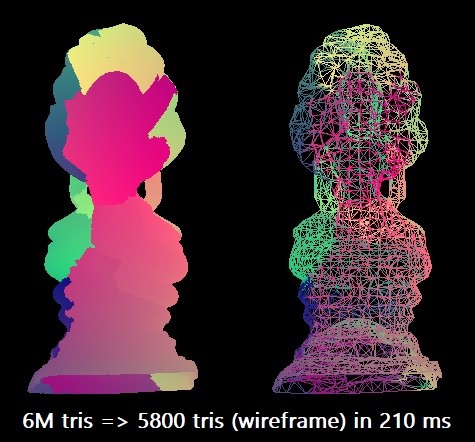
Pour notre référence, nous simplifions le modèle du Bouddha thaï de 6 millions de triangles à 0,1% de ce nombre. Nous utilisons le compilateur Microsoft Visual Studio 2019 pour l'architecture x64 cible. L'algorithme scalaire peut effectuer une telle rationalisation en environ 210 ms dans un seul thread Intel Core i7-8700K (à ~ 4,4 GHz). Cela correspond à environ 28,5 millions de triangles par seconde. Peut-être que cela suffit dans la pratique, mais j'étais curieux d'explorer les capacités maximales de l'équipement.
Dans certains cas, la procédure peut être parallélisée en divisant la grille en morceaux, mais pour cela, il est nécessaire de procéder à une analyse supplémentaire de la connectivité afin de maintenir les limites, donc pour l'instant nous nous limiterons à des optimisations purement SIMD.
Sept mesures
Pour comprendre les possibilités d'optimisation, nous effectuerons le profilage à l'aide d'Intel VTune. Exécutez la procédure 100 fois pour vous assurer qu'il y a suffisamment de données.

Ici, j'ai activé le mode microarchitecture pour fixer le temps d'exécution de chaque fonction, ainsi que pour trouver des goulots d'étranglement. On voit que la rationalisation se fait à l'aide d'un ensemble de fonctions, chacune nécessitant un certain nombre de cycles. La liste des fonctions est triée par heure. Les voici par ordre d'exécution pour rendre l'algorithme plus facile à comprendre:
rescalePositions normalise les positions de tous les sommets dans un seul cube pour préparer la quantification à l'aide de computeVertexIdscomputeVertexIds calcule un identifiant quantifié de 30 bits pour chaque sommet sur une grille uniforme d'une taille donnée, où chaque axe est quantifié sur une grille (taille de grille 10 bits, donc l'identifiant est 30)countTriangles calcule le nombre approximatif de triangles que l'innovateur créera pour une taille de grille donnée, en supposant l'union de tous les sommets dans une cellule de grillefillVertexCells remplit un tableau qui fillVertexCells tous les sommets aux cellules correspondantes; tous les sommets avec le même ID correspondent à une cellulefillCellQuadrics remplit la structure Quadric (matrice symétrique Quadric ) pour chaque cellule afin de refléter les informations agrégées sur la géométrie correspondantefillCellRemap calcule l'indice de sommet pour chaque cellule, en choisissant l'un des sommets de cette cellule et minimise la distorsion géométriquefilterTriangles affiche l'ensemble final de triangles selon les tables sommet-cellule-sommet construites précédemment; la traduction naïve peut produire en moyenne ~ 5% de triangles en double, donc la fonction filtre les doublons.
computeVertexIds et
countTriangles sont exécutés plusieurs fois: l'algorithme détermine la taille du maillage pour la fusion des sommets, effectue une recherche binaire accélérée pour atteindre le nombre cible de triangles (dans notre cas 6000) et calcule le nombre de triangles que chaque taille de maillage générera à chaque itération. Les autres fonctions sont lancées une fois. Dans notre fichier, cinq passes de recherche donnent un maillage cible de 40
3 .
VTune signale utilement que la fonction la plus gourmande en ressources est celle qui calcule les quadriques: cela prend presque la moitié du temps d'exécution total de 21 s. Il s'agit du premier objectif d'optimisation de SIMD.
SIMD pièce par pièce
Jetons un coup d'œil au code source de
fillCellQuadrics pour mieux comprendre ce qu'il calcule exactement:
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); float weight = single_cell ? 3.f : 1.f; Quadric Q; quadricFromTriangle(Q, vertex_positions[i0], vertex_positions[i1], vertex_positions[i2], weight); if (single_cell) { quadricAdd(cell_quadrics[c0], Q); } else { quadricAdd(cell_quadrics[c0], Q); quadricAdd(cell_quadrics[c1], Q); quadricAdd(cell_quadrics[c2], Q); } } }
La fonction parcourt tous les triangles, calcule une quadrique pour chacun d'eux et l'ajoute aux quadriques de chaque cellule. Quadrique - une matrice symétrique 4 × 4, présentée sous la forme de 10 nombres à virgule flottante:
struct Quadric { float a00; float a10, a11; float a20, a21, a22; float b0, b1, b2, c; };
Le calcul d'une quadrique nécessite de résoudre l'équation plane d'un triangle, de construire une matrice quadratique et de la peser en utilisant l'aire du triangle:
static void quadricFromPlane(Quadric& Q, float a, float b, float c, float d) { Q.a00 = a * a; Q.a10 = b * a; Q.a11 = b * b; Q.a20 = c * a; Q.a21 = c * b; Q.a22 = c * c; Q.b0 = d * a; Q.b1 = d * b; Q.b2 = d * c; Qc = d * d; } static void quadricFromTriangle(Quadric& Q, const Vector3& p0, const Vector3& p1, const Vector3& p2, float weight) { Vector3 p10 = {p1.x - p0.x, p1.y - p0.y, p1.z - p0.z}; Vector3 p20 = {p2.x - p0.x, p2.y - p0.y, p2.z - p0.z}; Vector3 normal = { p10.y * p20.z - p10.z * p20.y, p10.z * p20.x - p10.x * p20.z, p10.x * p20.y - p10.y * p20.x }; float area = normalize(normal); float distance = normal.x*p0.x + normal.y*p0.y + normal.z*p0.z; quadricFromPlane(Q, normal.x, normal.y, normal.z, -distance); quadricMul(Q, area * weight); }
Il semble qu'il existe de nombreuses opérations en virgule flottante, elles peuvent donc être parallélisées à l'aide de SIMD. Tout d'abord, nous représentons chaque vecteur comme un vecteur SIMD à 4 larges, et modifions également la structure
Quadric à 12 nombres à virgule flottante au lieu de 10 afin qu'elle s'intègre exactement dans trois registres SIMD (l'augmentation de la taille n'affecte pas les performances) et changeons l'ordre des champs afin que les calculs
quadricFromPlane est devenu plus uniforme:
struct Quadric { float a00, a11, a22; float pad0; float a10, a21, a20; float pad1; float b0, b1, b2, c; };
Ici, certains calculs, en particulier le produit scalaire, ne sont pas très cohérents avec les versions antérieures de SSE. Heureusement, une instruction pour un produit scalaire est apparue dans SSE4.1, ce qui est très utile pour nous.
static void fillCellQuadrics(Quadric* cell_quadrics, const unsigned int* indices, size_t index_count, const Vector3* vertex_positions, const unsigned int* vertex_cells) { const int yzx = _MM_SHUFFLE(3, 0, 2, 1); const int zxy = _MM_SHUFFLE(3, 1, 0, 2); const int dp_xyz = 0x7f; for (size_t i = 0; i < index_count; i += 3) { unsigned int i0 = indices[i + 0]; unsigned int i1 = indices[i + 1]; unsigned int i2 = indices[i + 2]; unsigned int c0 = vertex_cells[i0]; unsigned int c1 = vertex_cells[i1]; unsigned int c2 = vertex_cells[i2]; bool single_cell = (c0 == c1) & (c0 == c2); __m128 p0 = _mm_loadu_ps(&vertex_positions[i0].x); __m128 p1 = _mm_loadu_ps(&vertex_positions[i1].x); __m128 p2 = _mm_loadu_ps(&vertex_positions[i2].x); __m128 p10 = _mm_sub_ps(p1, p0); __m128 p20 = _mm_sub_ps(p2, p0); __m128 normal = _mm_sub_ps( _mm_mul_ps( _mm_shuffle_ps(p10, p10, yzx), _mm_shuffle_ps(p20, p20, zxy)), _mm_mul_ps( _mm_shuffle_ps(p10, p10, zxy), _mm_shuffle_ps(p20, p20, yzx))); __m128 areasq = _mm_dp_ps(normal, normal, dp_xyz);
Il n'y a rien de particulièrement intéressant dans ce code; nous utilisons abondamment des instructions de chargement / stockage non alignées. Bien que l'entrée de Vector3 puisse être alignée, il ne semble pas y avoir de pénalité notable pour les lectures non alignées. Veuillez noter que dans la première moitié des fonctions, les vecteurs ne sont pas utilisés, ce qui est bien - nos vecteurs ont trois composants, et dans certains cas un seul (voir calcul surfacesq / surface / distance), tandis que le processeur effectue 4 opérations en parallèle. Dans tous les cas, voyons comment la parallélisation a aidé.

Une centaine de démarrages de
fillCellQuadrics s'exécute désormais en 5,3 s au lieu de 9,8 s, ce qui permet d'économiser environ 45 ms sur chaque opération - pas mal, mais pas très impressionnant. Dans de nombreuses instructions, nous utilisons trois au lieu de quatre composants, ainsi qu'une multiplication précise, ce qui donne un délai assez important. Si vous avez déjà écrit des instructions pour SIMD, vous savez comment faire correctement le produit scalaire.
Pour ce faire, vous devez faire quatre vecteurs à la fois. Au lieu de stocker un vecteur complet dans un registre SIMD, nous utilisons trois registres - dans l'un, nous stockons quatre composantes de
x , dans l'autre nous stockons
et dans le troisième
z . Ici, quatre vecteurs sont nécessaires pour travailler à la fois: cela signifie que nous traiterons quatre triangles simultanément.
Nous avons de nombreux tableaux avec indexation dynamique. Habituellement, cela aide à transférer des données vers des tableaux préparés de composants
x /
y /
z (ou plutôt, généralement de petits registres SIMD sont utilisés, par exemple,
float x[8], y[8], z[8] , pour chacun des 8 sommets en entrée données: cela s'appelle AoSoA (tableaux de structures de tableaux) et donne un bon équilibre entre la localisation du cache et la facilité de chargement dans les registres SIMD), mais ici l'indexation dynamique ne fonctionnera pas très bien, alors chargez les données pour quatre triangles comme d'habitude, et transposez les vecteurs en utilisant un moyen pratique macro
_MM_TRANSPOSE .
Théoriquement, vous devez calculer chaque composante de quatre quadriques finies dans son propre registre SIMD (par exemple, nous aurons
__m128 Q_a00 avec quatre composantes de
a00 quadriques finies). Dans ce cas, les opérations sur les quadriques s'intègrent assez bien dans les instructions SIMD à 4 larges, et la conversion ralentit en fait le code - par conséquent, nous transposons uniquement les vecteurs initiaux, puis transposons les équations planes en arrière et exécutons le même code que nous avons utilisé pour calculer les quadriques, mais répétons-le quatre fois. Voici le code qui calcule ensuite les équations de l'avion (les parties restantes sont omises par souci de concision):
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; unsigned int i20 = indices[(i + 2) * 3 + 0]; unsigned int i21 = indices[(i + 2) * 3 + 1]; unsigned int i22 = indices[(i + 2) * 3 + 2]; unsigned int i30 = indices[(i + 3) * 3 + 0]; unsigned int i31 = indices[(i + 3) * 3 + 1]; unsigned int i32 = indices[(i + 3) * 3 + 2];
Le code est devenu un peu plus long: nous traitons maintenant quatre triangles à chaque itération, et nous n'avons plus besoin d'instructions SSE4.1 pour cela. En théorie, les unités SIMD devraient être utilisées plus efficacement. Voyons comment cela a aidé.

D'accord, ça va. Le code a très légèrement accéléré, bien que la fonction
fillCellQuadrics fonctionne désormais presque deux fois plus vite que la fonction d'origine sans SIMD, mais il n'est pas clair si cela justifie une augmentation significative de la complexité. Théoriquement, vous pouvez utiliser AVX2 et traiter 8 triangles par itération, mais ici, vous devrez continuer de tourner la boucle manuellement (idéalement, tout ce code est généré à l'aide d'ISPC, mais mes tentatives naïves pour le faire générer du bon code n'ont pas réussi: au lieu de charger / stocker des séquences il a constamment émis un rassemblement / diffusion, ce qui ralentit considérablement l'exécution). Essayons autre chose.
AVX2 = SSE2 + SSE2
L'AVX2 est un peu un ensemble d'instructions. Il possède des registres à virgule flottante sur 8 larges, et une instruction peut effectuer 8 opérations; mais en substance, une telle instruction ne diffère pas de deux instructions SSE2 exécutées sur deux moitiés du registre (pour autant que je sache, les premiers processeurs avec prise en charge AVX2 ont décodé chaque instruction en deux ou plusieurs micro-opérations, donc le gain de performances a été limité par la phase d'extraction des instructions). Par exemple,
_mm_dp_ps effectue un produit scalaire entre deux registres SSE2 et
_mm256_dp_ps produit deux produits scalaires entre deux moitiés de deux registres AVX2, il est donc limité à 4 larges pour chaque moitié.
Pour cette raison, le code AVX2 diffère souvent du «SIMD 8-wide» universel, mais ici il fonctionne en notre faveur: au lieu d'essayer d'améliorer la vectorisation en transposant des vecteurs 4-wide, nous revenons à la première version de SIMD et doublons la boucle en utilisant des instructions AVX2 au lieu de SSE2 / SSE4. Nous devons encore charger et stocker des vecteurs de largeur 4, mais en général, nous changeons simplement
__m128 en
__m256 et
_mm_ en
_mm256 dans le
_mm256 avec plusieurs paramètres:
unsigned int i00 = indices[(i + 0) * 3 + 0]; unsigned int i01 = indices[(i + 0) * 3 + 1]; unsigned int i02 = indices[(i + 0) * 3 + 2]; unsigned int i10 = indices[(i + 1) * 3 + 0]; unsigned int i11 = indices[(i + 1) * 3 + 1]; unsigned int i12 = indices[(i + 1) * 3 + 2]; __m256 p0 = _mm256_loadu2_m128( &vertex_positions[i10].x, &vertex_positions[i00].x); __m256 p1 = _mm256_loadu2_m128( &vertex_positions[i11].x, &vertex_positions[i01].x); __m256 p2 = _mm256_loadu2_m128( &vertex_positions[i12].x, &vertex_positions[i02].x); __m256 p10 = _mm256_sub_ps(p1, p0); __m256 p20 = _mm256_sub_ps(p2, p0); __m256 normal = _mm256_sub_ps( _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, yzx), _mm256_shuffle_ps(p20, p20, zxy)), _mm256_mul_ps( _mm256_shuffle_ps(p10, p10, zxy), _mm256_shuffle_ps(p20, p20, yzx))); __m256 areasq = _mm256_dp_ps(normal, normal, dp_xyz); __m256 area = _mm256_sqrt_ps(areasq); __m256 areanz = _mm256_cmp_ps(area, _mm256_setzero_ps(), _CMP_NEQ_OQ); normal = _mm256_and_ps(_mm256_div_ps(normal, area), areanz); __m256 distance = _mm256_dp_ps(normal, p0, dp_xyz); __m256 negdistance = _mm256_sub_ps(_mm256_setzero_ps(), distance); __m256 normalnegdist = _mm256_blend_ps(normal, negdistance, 0x88); __m256 Qx = _mm256_mul_ps(normal, normal); __m256 Qy = _mm256_mul_ps( _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 2, 2, 1)), _mm256_shuffle_ps(normal, normal, _MM_SHUFFLE(3, 0, 1, 0))); __m256 Qz = _mm256_mul_ps(negdistance, normalnegdist);
Ici, vous pouvez prendre chaque moitié de 128 bits des
Qz Qx /
Qz /
Qz et exécuter le même code que nous avons utilisé pour ajouter les quadriques. Au lieu de cela, nous supposons que si un triangle a trois sommets dans une cellule (
single_cell == true ), il est très probable qu'un autre triangle ait trois sommets dans une autre cellule, et nous effectuons également l'agrégation finale des quadriques en utilisant AVX2:
unsigned int c00 = vertex_cells[i00]; unsigned int c01 = vertex_cells[i01]; unsigned int c02 = vertex_cells[i02]; unsigned int c10 = vertex_cells[i10]; unsigned int c11 = vertex_cells[i11]; unsigned int c12 = vertex_cells[i12]; bool single_cell = (c00 == c01) & (c00 == c02) & (c10 == c11) & (c10 == c12); if (single_cell) { area = _mm256_mul_ps(area, _mm256_set1_ps(3.f)); Qx = _mm256_mul_ps(Qx, area); Qy = _mm256_mul_ps(Qy, area); Qz = _mm256_mul_ps(Qz, area); Quadric& q00 = cell_quadrics[c00]; Quadric& q10 = cell_quadrics[c10]; __m256 q0x = _mm256_loadu2_m128(&q10.a00, &q00.a00); __m256 q0y = _mm256_loadu2_m128(&q10.a10, &q00.a10); __m256 q0z = _mm256_loadu2_m128(&q10.b0, &q00.b0); _mm256_storeu2_m128(&q10.a00, &q00.a00, _mm256_add_ps(q0x, Qx)); _mm256_storeu2_m128(&q10.a10, &q00.a10, _mm256_add_ps(q0y, Qy)); _mm256_storeu2_m128(&q10.b0, &q00.b0, _mm256_add_ps(q0z, Qz)); } else {
Le code résultant est plus simple, concis et plus rapide que notre approche SSE2 infructueuse:

Bien sûr, nous n'avons pas atteint une accélération de 8 fois, mais seulement 2,45 fois. Les opérations de chargement et de stockage sont toujours à 4 niveaux, car nous sommes obligés de travailler avec une disposition de mémoire inconfortable en raison de l'indexation dynamique, et les calculs ne sont pas optimaux pour SIMD. Mais maintenant
fillCellQuadrics n'est plus le goulot d'étranglement dans notre pipeline de profils, et vous pouvez vous concentrer sur d'autres fonctions.
Rassemblez-vous, les enfants
Nous avons économisé 4,8 secondes lors du test (48 ms à chaque test), et maintenant notre principal intrus est
countTriangles . Il semblerait que ce soit une fonction simple, mais elle est exécutée non pas une fois, mais cinq fois:
static size_t countTriangles(const unsigned int* vertex_ids, const unsigned int* indices, size_t index_count) { size_t result = 0; for (size_t i = 0; i < index_count; i += 3) { unsigned int id0 = vertex_ids[indices[i + 0]]; unsigned int id1 = vertex_ids[indices[i + 1]]; unsigned int id2 = vertex_ids[indices[i + 2]]; result += (id0 != id1) & (id0 != id2) & (id1 != id2); } return result; }
La fonction énumère tous les triangles source et calcule le nombre de triangles non dégénérés en comparant les identifiants des sommets. Il n'est pas immédiatement clair comment le paralléliser à l'aide de SIMD ... sauf si vous utilisez les instructions de collecte.
Le jeu d'instructions AVX2 a ajouté une famille d'instructions de collecte / diffusion au SIMD x64; chacun d'eux prend un registre vectoriel avec 4 ou 8 valeurs - et effectue simultanément 4 ou 8 opérations de chargement ou de sauvegarde. Si vous utilisez recueillir ici, vous pouvez télécharger trois index, exécuter regrouper pour tous à la fois (ou en groupes de 4 ou 8) et comparer les résultats. Rassembler sur les processeurs Intel a toujours été assez lent, mais essayons. Par souci de simplicité, nous téléchargeons les données de 8 triangles, transposons les vecteurs de la même manière que lors de notre précédente tentative et comparons les éléments correspondants de chaque vecteur:
for (size_t i = 0; i < (triangle_count & ~7); i += 8) { __m256 tri0 = _mm256_loadu2_m128( (const float*)&indices[(i + 4) * 3 + 0], (const float*)&indices[(i + 0) * 3 + 0]); __m256 tri1 = _mm256_loadu2_m128( (const float*)&indices[(i + 5) * 3 + 0], (const float*)&indices[(i + 1) * 3 + 0]); __m256 tri2 = _mm256_loadu2_m128( (const float*)&indices[(i + 6) * 3 + 0], (const float*)&indices[(i + 2) * 3 + 0]); __m256 tri3 = _mm256_loadu2_m128( (const float*)&indices[(i + 7) * 3 + 0], (const float*)&indices[(i + 3) * 3 + 0]); _MM_TRANSPOSE8_LANE4_PS(tri0, tri1, tri2, tri3); __m256i i0 = _mm256_castps_si256(tri0); __m256i i1 = _mm256_castps_si256(tri1); __m256i i2 = _mm256_castps_si256(tri2); __m256i id0 = _mm256_i32gather_epi32((int*)vertex_ids, i0, 4); __m256i id1 = _mm256_i32gather_epi32((int*)vertex_ids, i1, 4); __m256i id2 = _mm256_i32gather_epi32((int*)vertex_ids, i2, 4); __m256i deg = _mm256_or_si256( _mm256_cmpeq_epi32(id1, id2), _mm256_or_si256( _mm256_cmpeq_epi32(id0, id1), _mm256_cmpeq_epi32(id0, id2))); result += 8 - _mm_popcnt_u32(_mm256_movemask_epi8(deg)) / 4; }
La macro
_MM_TRANSPOSE8_LANE4_PS dans AVX2 est l'équivalent de
_MM_TRANSPOSE4_PS , qui ne se trouve pas dans l'en-tête standard, mais est facilement affichée. Il prend quatre vecteurs AVX2 et transpose deux matrices 4 × 4 indépendamment l'une de l'autre:
#define _MM_TRANSPOSE8_LANE4_PS(row0, row1, row2, row3) \ do { \ __m256 __t0, __t1, __t2, __t3; \ __t0 = _mm256_unpacklo_ps(row0, row1); \ __t1 = _mm256_unpackhi_ps(row0, row1); \ __t2 = _mm256_unpacklo_ps(row2, row3); \ __t3 = _mm256_unpackhi_ps(row2, row3); \ row0 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(1, 0, 1, 0)); \ row1 = _mm256_shuffle_ps(__t0, __t2, _MM_SHUFFLE(3, 2, 3, 2)); \ row2 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(1, 0, 1, 0)); \ row3 = _mm256_shuffle_ps(__t1, __t3, _MM_SHUFFLE(3, 2, 3, 2)); \ } while (0)
En raison de certaines fonctionnalités des jeux d'instructions SSE2 / AVX2, nous devons utiliser des opérations de registre à virgule flottante lors de la transposition de vecteurs. Nous chargeons les données un peu négligemment; mais cela n'a pas d'importance, car les performances de collecte nous limitent:

Maintenant,
countTriangles est environ 27% plus rapide et remarque le terrible CPI (cycles par instruction): nous envoyons environ quatre fois moins d'instructions, mais rassembler prend beaucoup de temps. C'est génial que cela accélère le travail global, mais, bien sûr, le gain de performances est quelque peu déprimant. Nous avons réussi à dépasser
fillCellQuadrics dans le profil, ce qui nous amène à la dernière fonction en haut de la liste, que nous n'avons pas encore examinée.
Chapitre 6, où tout commence à fonctionner comme il se doit
La dernière fonction est
computeVertexIds . Dans l'algorithme, il est effectué 6 fois, il représente donc également un excellent objectif d'optimisation. Pour la première fois, nous voyons une fonction qui semble être créée pour une optimisation claire dans SIMD:
static void computeVertexIds(unsigned int* vertex_ids, const Vector3* vertex_positions, size_t vertex_count, int grid_size) { assert(grid_size >= 1 && grid_size <= 1024); float cell_scale = float(grid_size - 1); for (size_t i = 0; i < vertex_count; ++i) { const Vector3& v = vertex_positions[i]; int xi = int(vx * cell_scale + 0.5f); int yi = int(vy * cell_scale + 0.5f); int zi = int(vz * cell_scale + 0.5f); vertex_ids[i] = (xi << 20) | (yi << 10) | zi; } }
Après les optimisations précédentes, nous savons quoi faire: dérouler le cycle 4 ou 8 fois, car il ne sert à rien d'accélérer une seule itération, de transposer les composantes vectorielles et d'exécuter les calculs en parallèle. Faisons-le avec AVX2, en traitant 8 sommets à la fois:
__m256 scale = _mm256_set1_ps(cell_scale); __m256 half = _mm256_set1_ps(0.5f); for (size_t i = 0; i < (vertex_count & ~7); i += 8) { __m256 vx = _mm256_loadu2_m128( &vertex_positions[i + 4].x, &vertex_positions[i + 0].x); __m256 vy = _mm256_loadu2_m128( &vertex_positions[i + 5].x, &vertex_positions[i + 1].x); __m256 vz = _mm256_loadu2_m128( &vertex_positions[i + 6].x, &vertex_positions[i + 2].x); __m256 vw = _mm256_loadu2_m128( &vertex_positions[i + 7].x, &vertex_positions[i + 3].x); _MM_TRANSPOSE8_LANE4_PS(vx, vy, vz, vw); __m256i xi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vx, scale), half)); __m256i yi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vy, scale), half)); __m256i zi = _mm256_cvttps_epi32( _mm256_add_ps(_mm256_mul_ps(vz, scale), half)); __m256i id = _mm256_or_si256( zi, _mm256_or_si256( _mm256_slli_epi32(xi, 20), _mm256_slli_epi32(yi, 10))); _mm256_storeu_si256((__m256i*)&vertex_ids[i], id); }
Et regardez les résultats: nous avons accéléré
nous avons accéléré computeVertexIdsdeux fois. Compte tenu de toutes les optimisations, le temps total d'exécution du programme a été réduit à environ 120 ms, ce qui correspond au calcul de 50 millions de triangles par seconde.Il peut sembler que nous n'ayons pas encore atteint la croissance de productivité attendue: computeVertexIdsne devrait- elle pas accélérer plus de deux fois après la parallélisation? Pour répondre à cette question, essayons de voir combien de travail cette fonction effectue.computeVertexIdsIl est exécuté six fois pour un démarrage de programme: cinq fois pendant la recherche binaire et une fois à la fin pour calculer les identifiants finaux qui sont utilisés pour un traitement ultérieur. Chaque fois, cette fonction traite 3 millions de sommets, lisant 12 octets pour chaque sommet et écrivant 4 octets.Au total, sur plus de 100 exécutions de l'innovateur, cette fonction traite 1,8 milliard de sommets, lisant 21 Go et réécrivant 7 Go. Le traitement de 28 Go en 1,46 seconde nécessite une bande passante de bus de 19 Go / s. Nous pouvons vérifier la bande passante mémoire en exécutant memcmp(block1, block2, 512 MB). Le résultat est de 45 ms, soit environ 22 Go / s sur un seul cœur (bien que la référence AIDA64 montre des vitesses de lecture sur mon système jusqu'à 31 Go / s, mais il utilise plusieurs cœurs). En fait, nous nous sommes approchés de la limite de mémoire maximale réalisable, et une nouvelle augmentation des performances nécessitera un compactage plus étroit de ces sommets afin qu'ils occupent moins de 12 octets.Conclusion
Nous avons pris un algorithme assez bien optimisé qui simplifie les très grandes grilles à une vitesse de 28 millions de triangles par seconde, et avons utilisé les jeux d'instructions SSE et AVX pour l'accélérer presque deux fois, à 50 millions de triangles par seconde. Au cours de ce voyage, nous avons dû apprendre différentes façons d'utiliser SIMD: registres pour stocker des vecteurs à 3 larges, SoA transpose, instructions AVX2 pour stocker deux vecteurs à 3 larges, rassembler des instructions pour accélérer le chargement des données par rapport aux instructions scalaires, et enfin nous avons directement appliqué AVX2 pour le traitement en streaming.SIMD n'est souvent pas le meilleur point de départ pour l'optimisation: le rationaliseur de maillage a traversé de nombreuses itérations d'optimisation algorithmique et de microoptimisation sans utiliser d'instructions spécifiques à la plate-forme. Mais à un moment donné, ces possibilités sont épuisées, et si les performances sont critiques, alors SIMD est un outil fantastique qui peut être utilisé si nécessaire.Je ne sais pas laquelle de ces optimisations tombera dans la branche principale meshoptimizer: au final, ce n'est qu'une expérience pour voir combien le code est overclocké sans changement fondamental dans les algorithmes. J'espère que l'article s'est avéré être informatif et vous donnera des idées pour optimiser le code. Les sources finales de cet article sont ici ; ce travail est basé sur la version de meshoptimizer 99ab49et le modèle Thai Buddha est publié sur Sketchfab .