Présentation
Plusieurs articles [1,2,3] ont été publiés sur Habr et se rapportent directement ou indirectement à ce sujet. À cet égard, on ne peut manquer de noter la publication [1] avec le titre «Mathématiques sur les doigts: régulateur linéaire-quadratique», qui explique couramment le principe de fonctionnement du contrôleur LQR optimal.
Je voulais continuer ce sujet, après avoir examiné l'application pratique de la méthode d'optimisation dynamique, mais déjà sur un exemple concret utilisant Python. Tout d'abord, quelques mots sur la terminologie et la méthode d'optimisation dynamique.
Les méthodes d'optimisation sont divisées en statique et dynamique. L'objet de contrôle est dans un état de mouvement continu sous l'influence de divers facteurs externes et internes. Par conséquent, l'évaluation du résultat de contrôle est donnée pour le temps de contrôle T, et c'est une tâche d'optimisation dynamique.
En utilisant des méthodes d'optimisation dynamique, les problèmes associés à la distribution de ressources limitées sur une période de temps sont résolus, et la fonction objectif est écrite comme une fonction intégrale.
Les appareils mathématiques pour résoudre de tels problèmes sont des méthodes variationnelles: calcul classique des variations, principe du maximum L.S. Pontryagin et programmation dynamique R. Bellman.
L'analyse et la synthèse des systèmes de contrôle sont effectuées dans le temps, la fréquence et les espaces d'état. L'analyse et la synthèse des systèmes de contrôle dans l'espace d'état sont introduites dans le programme d'études, mais les techniques présentées dans les supports de formation utilisant le contrôleur SQR sont conçues pour Matlab et ne contiennent pas d'exemples pratiques d'analyse.
Le but de cette publication est d'examiner les méthodes d'analyse et de synthèse des systèmes de contrôle linéaires dans l'espace d'état en utilisant l'exemple bien connu d'optimisation du système de contrôle d'un moteur électrique et d'un avion en utilisant le langage de programmation Python.
Justification mathématique de la méthode d'optimisation dynamique
Pour l'optimisation, les critères d'amplitude (MO), symétrique (CO) et compromis optimum (KO) sont utilisés.
Lors de la résolution de problèmes d'optimisation dans l'espace d'état, un système stationnaire linéaire est donné par des équations matricielles vectorielles:
dotx= fracdxdt=A cdotx+B cdotu;y=C cdotx, (1)
Les critères intégrés pour la consommation d'énergie minimale de commande et la vitesse maximale sont fixés par les fonctions:
Jx= int infty0(xTQx+uTRu+2xTNu)dt rightarrowmin, (2)
Ju= int infty0(yTQy+uTRu+2yTNu)dt rightarrowmin. (3)
La loi de commande u se présente sous la forme d'une rétroaction linéaire sur les variables d'état x ou sur les variables de sortie y:
u= pmKx,u= pmKyUn tel contrôle minimise les critères de qualité quadratiques (2), (3). Dans les relations (1) ÷ (3), Q et R sont des matrices définies positives symétriques de dimension [n × n] et [m × m], respectivement; K est une matrice de coefficients constants de dimension [m × n], dont les valeurs ne sont pas limitées. Si le paramètre d'entrée N est omis, il est considéré comme nul.
La solution à ce problème, appelé problème d'optimisation quadratique intégrale linéaire (optimisation LQR), dans l'espace d'état est déterminée par l'expression:
u=R−1BTPxoù la matrice P doit satisfaire l'équation de Ricatti:
ATP+PA+PBR−1BTP+Q=0Les critères (2), (3) sont également contradictoires, car la mise en œuvre du premier terme nécessite une source de puissance infiniment élevée, et pour le second, une source de puissance infiniment basse. Cela peut s'expliquer par l'expression suivante:
Jx= int infty0xTQxdt ,
qui est la norme
Mod(x) vecteur x, c'est-à-dire une mesure de son oscillation dans le processus de régulation, et, par conséquent, prend des valeurs plus petites dans les transitoires rapides avec moins d'oscillation, et l'expression:
Ju= int infty0uTRudtest une mesure de la quantité d'énergie utilisée pour le contrôle; c'est une pénalité pour les coûts énergétiques du système.
Les matrices de poids Q, R et N déterminent les contraintes des coordonnées correspondantes. Si un élément de ces matrices est égal à zéro, la coordonnée correspondante n'a aucune restriction. En pratique, le choix des valeurs des matrices Q, R, N est effectué par la méthode des expertises, essais, erreurs et dépend de l'expérience et des connaissances de l'ingénieur d'études.
Pour résoudre ces problèmes, les opérateurs MATLAB suivants ont été utilisés:
beginbmatrixR,S,E endbmatrix=lqr(A,B,Q,R,N) et
beginbmatrixR,S,E endbmatrix=lqry(Ps,Q,R,N) qui minimisent les fonctionnelles (2), (3) par le vecteur d'état x ou par le vecteur de sortie y.
Modèle d'objet de gestion
Ps=ss(A,B,C,D). Le résultat du calcul est la matrice K de rétroactions optimales par rapport aux variables d'état x, la solution de l'équation de Ricatti S et les valeurs propres E = eiq (A-BK) du système de contrôle en boucle fermée.
Composants fonctionnels:
Jx=x0TP1x0,Ju=x0TP2x0où x0 est le vecteur des conditions initiales;
P1 et
P2 - matrices inconnues qui sont une solution des équations matricielles de Lyapunov. Ils sont trouvés en utilisant des fonctions;
P1=lyap(NN,Q) et
P2=lyap(NN,KTRK) ,
NN=(A+BK)TCaractéristiques de l'implémentation de la méthode d'optimisation dynamique à l'aide de Python
Bien que la bibliothèque de systèmes de contrôle Python [4] ait des fonctions: control.lqr, control.lyap, l'utilisation de control.lqr n'est possible que si le module slycot est installé, ce qui est un problème [5]. Lors de l'utilisation de la fonction lyap dans le contexte d'une tâche, l'optimisation se traduit par un control.exception.ControlArgument: Q doit être une erreur de matrice symétrique [6].
Par conséquent, pour implémenter les fonctions lqr () et lyap (), j'ai utilisé scipy.linalg:
from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)
À propos, vous ne devez pas abandonner complètement le contrôle, car les fonctions step (), pole (), ss (), tf (), feedback (), acker (), place () et d'autres fonctionnent bien.
Un exemple d'optimisation LQR dans un entraînement électrique
(un exemple est tiré de la publication [7])Considérons la synthèse d'un contrôleur linéaire-quadratique qui satisfait au critère (2) pour un objet de contrôle défini dans l'espace d'état par des matrices:
A = \ begin {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\\ end {bmatrix}; C = \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0
Les éléments suivants sont considérés comme des variables d'état:
x1 - tension du convertisseur, V;
x2 - courant moteur, A;
x3 - vitesse angulaire
c−1 . Il s'agit du système TP-DPT avec HB: moteur R nom = 30 kW; Unom = 220 V; Inom = 147 A ;;
omegaω 0 = 169
c−1 ;
omegaω max = 187
c−1 ; moment de résistance nominal Mnom = 150 N * m; multiplicité du courant de démarrage = 2; convertisseur thyristor: Unom = 230 V; Uy = 10 B; Inom = 300 A; multiplicité de surintensité de courte durée = 1,2.
Pour résoudre le problème, nous acceptons la matrice Q diagonale. À la suite de la modélisation, il a été constaté que les valeurs minimales des éléments matriciels R = 84, et
Q=[[0,01,0,0],[0,0,01,0],[0,0,0.01]]. Dans ce cas, un processus de transition monotone de la vitesse angulaire du moteur est observé (Fig. 1). À R = 840
Q=[[0,01,0,0],[0,0,01,0],[0,0,0.01]] processus transitoire (Fig. 2) répond au critère MO. Le calcul des matrices P1 et P2 a été effectué à x0 = [220 147 162].
Liste du programme (Fig. 1). 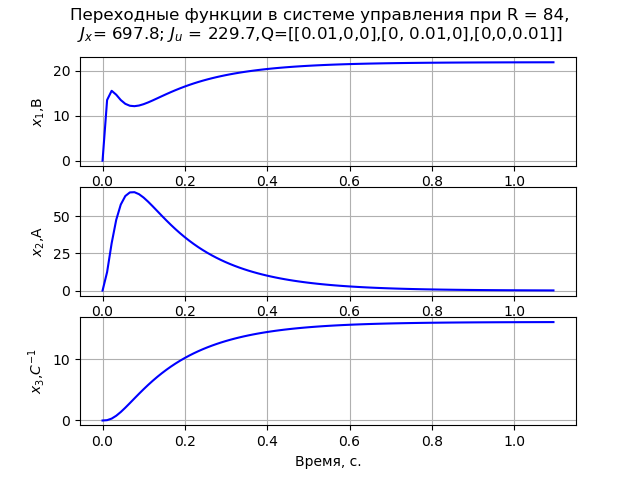 Fig. 1
Fig. 1Liste du programme (Fig. 2). 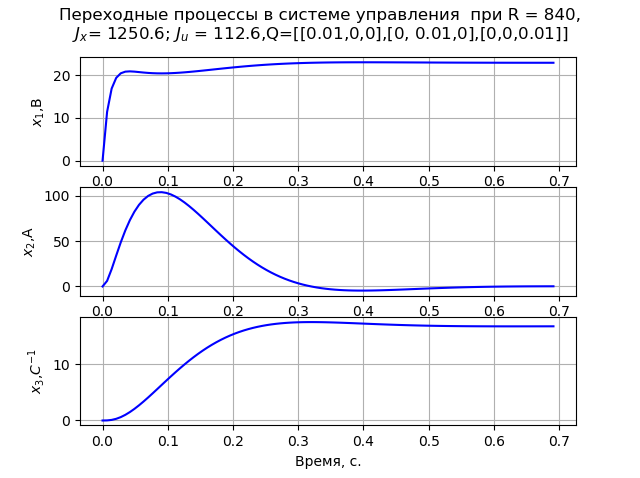 Fig. 2
Fig. 2Par une sélection appropriée des matrices R et Q, il est possible de réduire le courant de démarrage du moteur à des valeurs acceptables égales à (2–2,5) In (Fig. 3). Par exemple, avec R = 840 et
Q = ([[[0.01,0,0]], [0,0.88,0], [0,0,0.01]], sa valeur est de 292 A et le temps du processus de transition dans ces conditions est de 1,57 s.
Liste du programme (Fig. 3). 
Fig.3
Dans tous les cas considérés, les retours sur tension et courant sont négatifs, et sur la vitesse, positifs, ce qui n'est pas souhaitable selon les exigences de stabilité. De plus, le système synthétisé est astatique pour la tâche et statique pour la charge. Par conséquent, nous considérons la synthèse d'un contrôleur PI dans l'espace d'état avec une variable d'état supplémentaire
x4 - coefficient de transfert de l'intégrateur.
Nous représentons les informations initiales sous forme de matrices:
A = \ begin {bmatrix} & -100 & 0 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 0 & 1 & 0 \ end {bmatrix}; B = \ begin {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix}; C = œil (4)); D = 0Les transitoires de tâche correspondant au critère MO ont été obtenus à R = 100, q11 = q22 = q33 = 0,001 et q44 = 200. La figure 4 montre les variables d'état transitoires confirmant l'astatisme du système par tâche et par charge.
Liste des programmes (Fig.4). 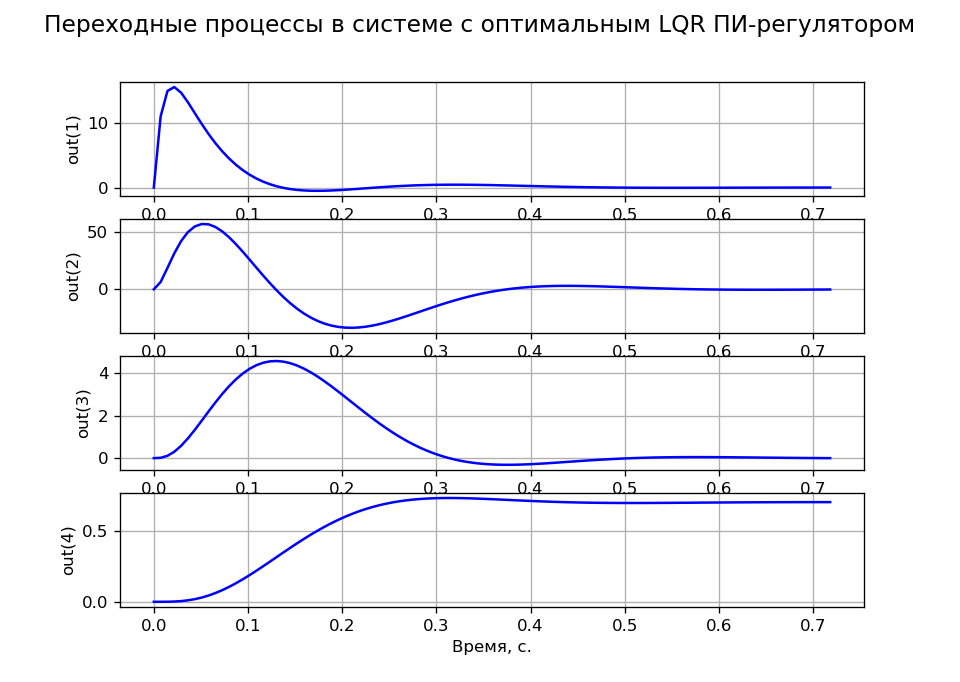 Fig. 4
Fig. 4Pour déterminer la matrice K, la bibliothèque des systèmes de contrôle Python a deux fonctions K = acker (A, B, s) et K = place (A, B, s), où s est le vecteur - la ligne des pôles souhaités de la fonction de transfert du système de contrôle en boucle fermée. La première commande ne peut être utilisée que pour les systèmes avec une entrée en u pour n≤5. Le second n'a pas de telles restrictions, mais la multiplicité des pôles ne doit pas dépasser le rang de la matrice B. Un exemple d'utilisation de l'opérateur acker () est illustré dans la liste et dans (Fig. 5).
Liste des programmes (Fig.5).  Fig. 5
Fig. 5Conclusion
La mise en œuvre de l'optimisation LQR de l'entraînement électrique donnée dans la publication, en tenant compte de l'utilisation des nouvelles fonctions lqr () et lyap (), nous permettra d'abandonner l'utilisation du programme sous licence MATLAB lors de l'étude de la section correspondante de la théorie du contrôle.
Un exemple d'optimisation LQR dans un avion (LA)
(un exemple est tiré de la publication d'Astrom et Mruray, chapitre 5 [8] et finalisé par l'auteur de l'article en termes de remplacement de la fonction lqr () et de réduction de la terminologie à celle généralement acceptée)La partie théorique, une brève théorie, l'optimisation LQR a déjà été considérée ci-dessus, alors passons à l'analyse de code avec les commentaires correspondants:
Bibliothèques requises et fonction de contrôleur LQR. from scipy.linalg import*
Conditions initiales et matrices de base Modèles A, B, C, D. xe = [0, 0, 0, 0, 0, 0];
Nous construisons des entrées et des sorties correspondant aux changements pas à pas de la position xy. Les vecteurs xd et yd correspondent à l'état stationnaire souhaité dans le système. Les matrices Cx et Cy sont les sorties correspondantes du modèle. Pour décrire la dynamique du système, nous utilisons un système d'équations à matrice vectorielle:
\ left \ {\ begin {matrix} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {matrix} \ à droite.
La dynamique d'une boucle fermée peut être modélisée à l'aide de la fonction step (), pour K \ cdot xd et K \ cdot xd comme vecteurs d'entrée, où:
xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);
La bibliothèque actuelle de contrôle 0.8.1 ne prend en charge qu'une partie des fonctions SISO Matlab pour créer des contrôleurs de rétroaction.Par conséquent, pour lire les données du contrôleur, il est donc nécessaire de créer des vecteurs d'indexation lat (), alt () pour la dynamique latérale -x et verticale -y.
lat = (0,2,3,5); alt = (1,4);
Les graphiques sont affichés séquentiellement, un pour chaque tâche.
figure(); title(" x y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()
Graphique: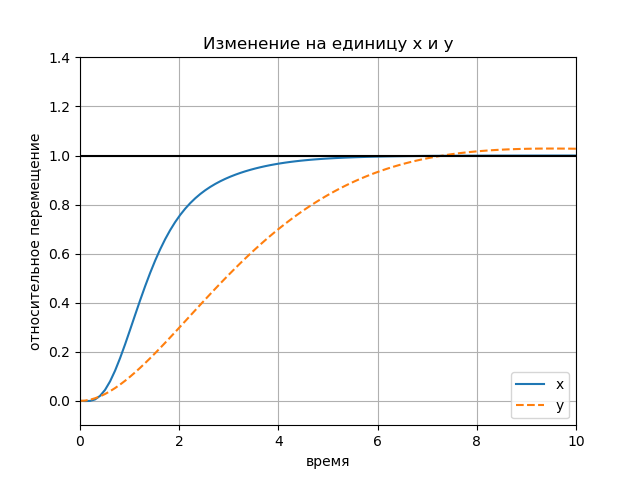
L'influence de l'amplitude des actions d'entrée Graphique: Graphique:
Graphique: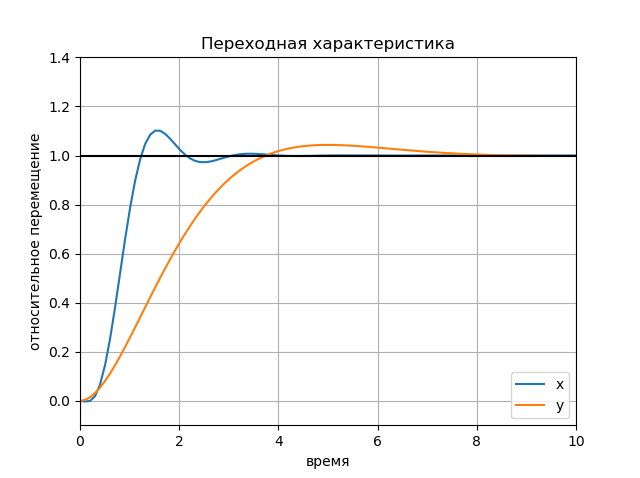
Réponse transitoire à base physique Graphique: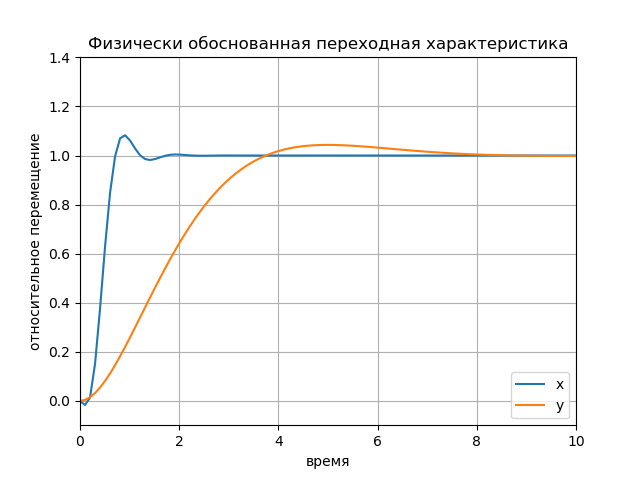
Conclusion:
La mise en œuvre de l'optimisation LQR dans l'avion présenté dans la publication, en tenant compte de l'utilisation de la nouvelle fonction lqr (), nous permettra d'abandonner l'utilisation du programme sous licence MATLAB lors de l'étude de la section correspondante de la théorie du contrôle.
Les références
1.
Mathématiques sur les doigts: contrôleur linéaire-quadratique.2.
L'espace d'état dans les problèmes de conception de systèmes de contrôle optimaux.3.
Utilisation de la bibliothèque de systèmes de contrôle Python pour concevoir des systèmes de contrôle automatique.4.
Bibliothèque de systèmes de contrôle Python.5.
Python - ne peut pas importer le module slycot dans spyder (RuntimeError & ImportError).6.
Bibliothèque de systèmes de contrôle Python.7.
Critères pour un contrôle optimal et une optimisation lqr dans un entraînement électrique.