Comment un puzzle pour enfants aide à révéler les secrets du magnétisme

Les aimants sont connus des gens depuis l'Antiquité, mais la physique du ferromagnétisme reste un mystère. Maintenant, un puzzle familier rapproche les physiciens des réponses aux questions

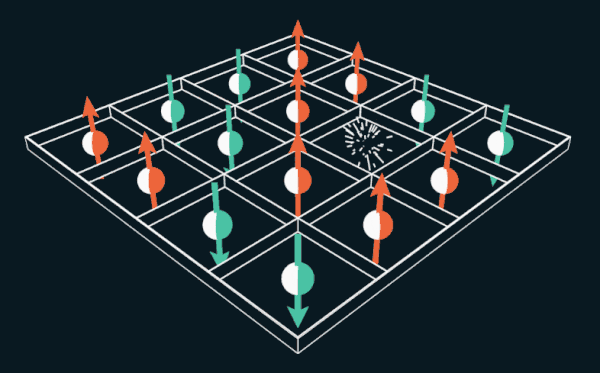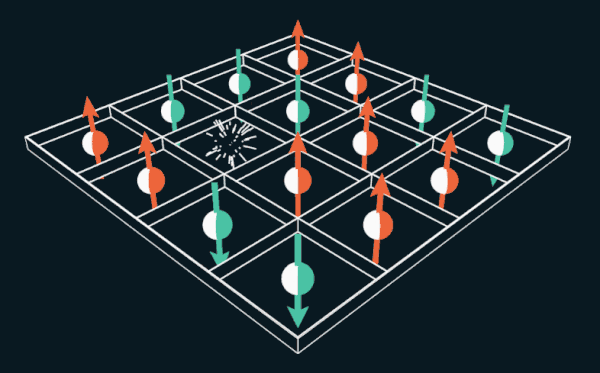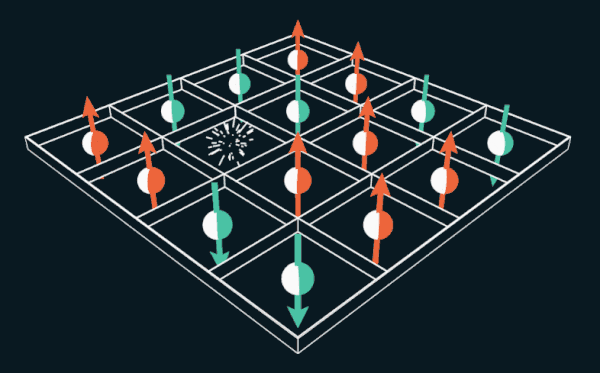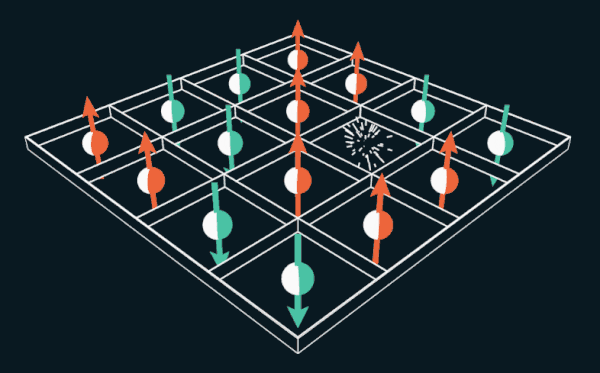Le jeu de 15 propose au joueur de déplacer les tuiles numérotées dans la grille. Si vous remplacez les nombres par les spins d'électrons, le puzzle peut être utilisé pour expliquer le fonctionnement des aimants permanents.

Pendant plusieurs mois au cours de l'année 1880, des régions entières des États-Unis ont succombé à la dépendance, dont personne n'avait jamais vu d'analogues auparavant. "Une épidémie a littéralement éclaté à travers le pays", écrit le magazine The Weekly News-Democrat à Imperia, Kansas, le 12 mars 1880. "Des villes entières sont attirées, les gens perdent le sommeil et deviennent fous." L'épidémie s'est propagée en Europe et a même atteint l'Australie avec la Nouvelle-Zélande.

La maladie est devenue une nouvelle passion: décourager le simple puzzle mécanique "15". Il est encore connu et se compose d'un champ carré 4x4 dans lequel vous pouvez déplacer 15 tuiles numérotées afin de les disposer dans l'ordre.

Selon les normes d'aujourd'hui, le jeu semble démodé, mais en 1880, il était au sommet de sa popularité. "Aucun enfant ne peut résister à un tel divertissement, aucun adulte ne sera aussi fort ou arrogant pour échapper à son charme", écrit le journal. Et la déception peut provenir du fait mathématiquement prouvé que seule la moitié des configurations de ce puzzle peut être résolue avec succès (ce qui était probablement inconnu de ceux qui ont subi son influence).

Aujourd'hui, près de 140 ans plus tard, l'intérêt pour le jeu "15" a repris, mais cette fois-ci, il ne s'agit pas d'une distraction, mais d'un moyen de comprendre un puzzle apparemment sans rapport et beaucoup plus compliqué: le fonctionnement des aimants.

Les aimants permanents, comme ceux accrochés à la porte de votre réfrigérateur, sont attirés par un phénomène tel que le ferromagnétisme . Dans un ferromagnet, les spins des électrons sont alignés, et ensemble ils génèrent un champ magnétique. Plus précisément, les métaux tels que le fer, le cobalt et le nickel présentent un magnétisme à bande, car leurs électrons sont capables de se déplacer librement dans le matériau. Chaque électron a son propre moment magnétique, mais pour comprendre comment et pourquoi tous ces moments s'alignent dans un aimant, il est nécessaire de calculer les interactions quantiques entre tous les électrons, ce qui est excessivement difficile à faire.

«Le magnétisme de zone est en fait l'un des plus grands défis de la physique théorique de la matière condensée», a déclaré Wai Lee, physicien à l'Université Johns Hopkins.

Cependant, Lee et deux étudiants diplômés, Eric Bobrov et Keaton Stewbis, se sont peut-être rapprochés un peu plus de ce problème. En utilisant le casse-tête mathématique "15", ils ont développé le théorème bien connu décrivant l'état idéalisé du magnétisme de zone. Dans leur nouvelle analyse , publiée dans Physical Review B, ils étendent le théorème pour expliquer un système plus large et plus réaliste, ce qui pourrait potentiellement conduire à un modèle d'aimants plus précis.

"C'est un excellent travail", a déclaré Daniel Arovas , physicien à l'Université de Californie à San Diego. «J'aime particulièrement ce travail car il y a trop peu de résultats détaillés concernant le magnétisme de zone et ils sont trop fragmentés.»

Saut de trou

Au niveau le plus élémentaire, les électrons dans un métal doivent obéir à deux restrictions majeures. Premièrement, ils sont tous chargés négativement, ils se repoussent donc. Deuxièmement, les électrons doivent obéir à ce que l'on appelle le principe de Pauli, qui postule que deux particules [avec un spin demi-entier / env. trans.] ne peut pas être dans le même état quantique. Cela signifie que les électrons avec le même spin - proportionnels au moment magnétique d'un électron - ne peuvent pas occuper le même état dans un atome métallique. Et deux électrons avec des spins opposés le peuvent.

Il s'avère que le moyen le plus simple de satisfaire à la fois la répulsion mutuelle et les limites du principe de Pauli pour un groupe d'électrons sera de séparer et d'aligner les spins - à la suite de quoi le matériau devient ferromagnétique.

Cependant, ce n'est qu'une image simplifiée. Les physiciens n'ont pas pu construire un modèle détaillé de l'apparition d'un tel modèle organisé de spins alignés à partir d'innombrables interactions quantiques entre les électrons individuels. Par exemple, comme Lee l'a expliqué, la fonction d'onde d'un électron - une description mathématique complexe de ses propriétés quantiques - peut être confondue avec la fonction d'onde d'un autre électron. Pour bien comprendre comment le comportement de particules individuelles conduit à l'apparition d'un phénomène collectif tel que le ferromagnétisme, vous devrez surveiller la fonction d'onde de chaque électron dans le système, tandis qu'il modifie en permanence la fonction d'onde de chacun des électrons restants au cours de leur interaction. Dans la pratique, cet enchevêtrement omniprésent rend impossible l'écriture des équations complètes et complètes nécessaires pour décrire le ferromagnétisme.

Au lieu de cela, les physiciens, y compris Lee, tentent de recueillir des informations en étudiant des modèles simplifiés et idéalisés qui décrivent la physique derrière le ferromagnétisme. En particulier, son dernier travail prolonge une découverte importante faite il y a plus de 50 ans.

Au milieu des années 1960, deux physiciens des côtés opposés du globe ont obtenu des preuves indépendantes prouvant pourquoi les électrons devraient s'aligner et créer un état ferromagnétique. David Tules, alors physicien qui travaillait à l'Université de Cambridge et a finalement remporté le prix Nobel 2016, et Yosuke Nagaoka, physicien à l'Université de Nagoya qui visitait alors l'Université de Californie à San Diego, ont publié leurs témoignages en 1965 et 1966, respectivement. . Leur résultat, appelé le théorème de Nagaoki-Tules (ou simplement le théorème de Nagaoki), est basé sur un système idéalisé d'électrons situés sur un réseau atomique. Ainsi, bien qu'il n'explique pas le comportement des aimants réels, il était toujours important, montrant pour la première fois en principe pourquoi les spins d'électrons devaient être alignés. Et puisque leur analyse était une preuve mathématique, ils étaient exacts, pas surchargés d'approximations typiques de la physique.

Pour comprendre le théorème, imaginez un réseau carré à deux dimensions. Chaque nœud peut placer deux électrons avec des spins opposés, mais le théorème suggère que placer deux électrons en un seul endroit nécessitera une quantité infinie d'énergie. Cela garantit qu'un seul électron sera à chaque endroit. Dans cette configuration, chaque électron peut diriger son spin vers le haut ou vers le bas. Ils n'ont pas à s'aligner, un tel système ne doit donc pas être un ferromagnet.


Wai Lee, physicien à l'Université Johns Hopkins

Maintenant, nous supprimons un électron. En conséquence, il y aura un endroit vacant appelé trou. Un électron voisin peut se glisser dans un trou, laissant derrière lui un nouvel espace vide. Un autre électron peut se déplacer vers un nouvel endroit vide, laissant un autre trou derrière. Dans cet exemple, un trou, en fait, saute d'un endroit à un autre, se déplaçant autour de la grille. Thules et Nagaoka ont constaté que dans ce cas, lorsqu'un seul trou est ajouté, les électrons s'aligneront spontanément. Ils ont prouvé que ce serait l'état avec le moins d'énergie, l'état d'un ferromagnet.

Arovas explique que pour qu'un système entre dans un état avec l'énergie la plus basse, un trou doit pouvoir se déplacer librement sans perturber la configuration des spins électroniques - un tel processus nécessitera de l'énergie supplémentaire. Mais quand un trou se déplace, les électrons doivent également se déplacer. Pour que les électrons se déplacent sans perturber la configuration des spins, ils doivent être alignés.

"Le théorème de Nagaoka est l'un des rares exemples qui peuvent prouver mathématiquement des cas individuels de ferromagnétisme", a déclaré Masaki Oshikawa , physicien à l'Université de Tokyo. "Mais du point de vue de la physique, tout cela est très artificiel."

Par exemple, les électrons ont besoin de beaucoup d'énergie pour surmonter leur répulsion mutuelle et s'installer en un seul endroit - mais pas infini, comme l'exige le théorème. De plus, l'image dessinée par Nagaoka et Tules ne s'applique qu'aux réseaux simples: les réseaux bidimensionnels constitués de carrés ou de triangles, ou les réseaux cubiques tridimensionnels. Dans la nature, le ferromagnétisme apparaît dans de nombreux métaux avec des structures de toutes sortes.

Si le théorème de Nagaoka-Tules explique réellement le ferromagnétisme, alors il devrait être applicable à tous les réseaux. Les gens pensaient que c'était le cas, a déclaré Lee. "Mais personne n'a donné de preuves réelles et claires." Eh bien, c'est encore.

Carreaux avec dos

En 1989, Hal Tasaki, physicien à l'Université Gakushuin du Japon, a étendu ce théorème pour trouver qu'il serait applicable tant que le réseau a une propriété mathématique telle que la connectivité. Prenons le cas simple d'un réseau carré avec un trou mobile. Si, en déplaçant un trou, vous pouvez reproduire n'importe quelle configuration de spins, en gardant le nombre d'électrons, avec des spins dirigés à la fois vers le haut et vers le bas, alors la condition de connexion est satisfaite.

Mais à part les réseaux carrés et triangulaires et les cubes tridimensionnels, il n'était pas clair si la condition liée serait satisfaite dans d'autres cas - et, par conséquent, dans quelle mesure ce théorème pouvait être appliqué.

Pour faire face à ce problème, Lee a commencé avec une grille hexagonale en nid d'abeille. Ses élèves, Bobrov et Stubis, travaillant sur cette tâche, ont réalisé qu'elle ressemble à une manie du XIXe siècle: le puzzle "15". Échangez les étiquettes des tuiles des nombres vers les dos, de haut en bas, et le puzzle devient équivalent au ferromagnet Nagaoki, avec un trou se déplaçant le long du réseau d'électrons.

Le casse-tête est autorisé lorsque vous avez la possibilité de redistribuer les tuiles dans n'importe quelle séquence, ce qui coïncide pleinement avec la condition de connectivité. Ainsi, la question de savoir si la condition de connexité est satisfaite pour un réseau donné devient la question de savoir s'il est possible de résoudre un puzzle équivalent sur un réseau d'une telle structure.

Il s'avère qu'en 1974, le mathématicien Richard Wilson, qui travaille maintenant au California Institute of Technology, a résolu ce problème en résumant et en résolvant le casse-tête «15» pour toutes les grilles. Dans le cadre de la preuve, il a montré que sur presque tous les réseaux inséparables (dans lesquels tous les nœuds restent connectés même après en avoir retiré un), vous pouvez déplacer les tuiles et obtenir n'importe quelle configuration, tandis que le nombre de mouvements reste uniforme. La seule exception est que les polygones simples sont plus grands qu'un triangle, et quelque chose appelé «graphique θ nul», dans lequel le sommet au centre de l'hexagone est connecté à deux sommets opposés.

Les chercheurs ont pu appliquer directement la preuve de Wilson au théorème de Nagaoka-Tules. Ils ont prouvé que la condition de connectivité est satisfaite pour un système d'électrons et un seul trou sur presque tous les réseaux, y compris des structures communes comme les nids d'abeilles bidimensionnels et les réseaux tridimensionnels en forme de diamant. Deux exceptions - des polygones plus grands qu'un triangle et le graphique θ nul - ne se produisent en tout cas pas dans les ferromagnétiques réels.

Explosion de trou

L'utilisation du casse-tête «15» est une approche nouvelle et potentiellement fructueuse, a déclaré Sriram Shastri , physicien à l'Université de Californie à Santa Cruz. «J'aime le fait qu'il a mis au travail un nouveau langage, un nouvel ensemble de connexions avec la théorie des graphes», a-t-il déclaré. "Je pense que c'est une connexion riche - à l'avenir, il pourrait devenir une riche source d'idées." Mais, bien que la recherche fasse un grand pas en avant, des problèmes subsistent.

Une complication est que le théorème de Nagaoki-Tules ne fonctionne pas toujours quand un trou en mouvement doit faire un nombre impair de pas tout en se déplaçant le long du réseau, a déclaré Shastri. Le problème peut-être le plus frappant est que le théorème requiert la présence d'un seul trou - ni plus, ni moins. Cependant, les métaux sont pleins de trous; ils occupent souvent jusqu'à la moitié du réseau.

Mais les physiciens ont tenté de généraliser le théorème pour les systèmes à nombreux trous. En utilisant des méthodes numériques, les physiciens ont montré que le ferromagnétisme de Nagaoki semble fonctionner pour un réseau carré de taille finie, dont jusqu'à 30% sont des trous. Dans les travaux en cours, les chercheurs ont appliqué des techniques analytiques précises aux nids d'abeilles bidimensionnels et aux réseaux tridimensionnels en forme de diamant. Le ferromagnétisme nagaoki existe, apparemment, tant que le nombre de trous ne dépasse pas le nombre de nœuds de réseau au degré 1/2 pour les cellules et au degré 2/5 pour le réseau en forme de diamant.

Ces solutions exactes peuvent conduire à un modèle plus complet de magnétisme de zone. "Ce n'est qu'un petit pas vers l'établissement d'un point de départ mathématique rigoureux pour la recherche future", a déclaré Lee.