Il y a quelques jours, j'ai eu un
concours en ligne pour le jeu .
1 199 personnes ont participé au concours en ligne, et il y a eu plus de 5 000 décisions, dont 61 ont tenté de contourner le système en trouvant des vulnérabilités. C'est très cool, merci à tous ceux qui ont participé.
Ce jeu est un type de «
jeux du colonel Blotto ». Deux joueurs y participent. Chacun a le même nombre de ressources qui doivent être placées sur le champ NxM. Le gagnant est celui qui prend le plus de cellules (c'est-à -dire que le nombre de vos ressources dessus est supérieur à celui de l'adversaire). Telle est la condition de notre tâche
Condition1. Deux jouent.
2. Le terrain de jeu est un plateau de 3 par 3.
3. Chaque joueur a une armée de 100 Space Marines.
4. Avant la bataille de nuit, chaque camp place secrètement ses troupes de façon aléatoire sur 9 cellules. Sur chaque cellule, vous pouvez mettre n'importe quel nombre entier de Space Marines de 0 à 100.
5. Le matin, la bataille pour la prochaine planète commence. Sur chacune des 9 cellules, le joueur qui a le plus d'Astartes sur cette cellule gagne. Pour une victoire sur chacune des 9 cellules, 1 point est accordé. Si le même nombre est sur une certaine case, la bataille sur cette case se termine par un match nul, et les deux joueurs obtiennent 0,5 point.
6. La bataille est gagnée par celui qui a gagné le plus de champs. Si les deux joueurs ont remporté 4,5 champs, la bataille se termine par un match nul.
Quand j'ai commencé cette expérience, je ne savais toujours pas que ce jeu n'avait pas de solution idéale, mais grâce aux commentaires j'ai pu mieux comprendre ce sujet.
Commençons par les gagnants de ce jeu.
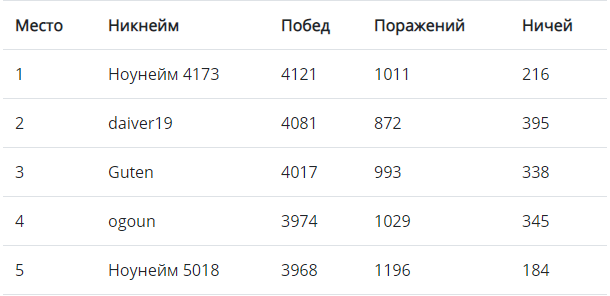
La meilleure décision a marqué 4121 victoires - un très bon résultat. Mais que se passerait-il si seules les solutions TOP-100 participaient au jeu?
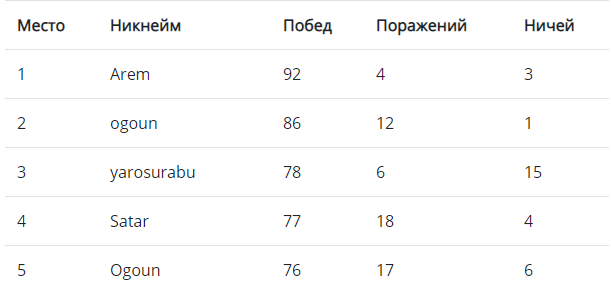
Étonnamment, il n'est même pas entré dans le top5 (à la 8e place), et la première place a été prise par la décision de la 68e place.
Cela montre simplement qu'il n'y a pas de meilleure solution. D'autres résultats peuvent être consultés sur
game.pavlukhinlab.comMais que pouvez-vous apprendre d'autre?
Les joueurs ont placé les plus grands nombres au centre, en moyenne, tous les joueurs ont rempli la première ligne avec de grands nombres, tandis que les meilleurs résultats ont mis davantage l'accent sur la ligne du bas.
valeurs moyennes pour tous les jeux (à gauche) et TOP-100 (à droite)Eh bien, et plus d'exemples des meilleures stratégies:
Exemples de stratégies Ogoun (6 solutions dans le TOP-100) Exemples de stratégies Guten (8 solutions dans le TOP-100) Les meilleures stratégies ont sélectionné 5 cellules principales, les cellules restantes ont été remplies de petites valeurs. Ce qui est logique, car pour gagner il suffit de prendre 5 cellules.
Eh bien, maintenant quelques graphiques.
Distribution probabiliste des nombres:
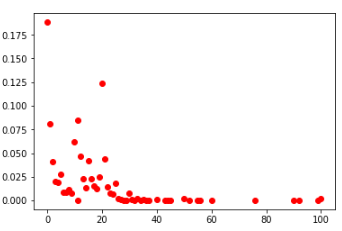
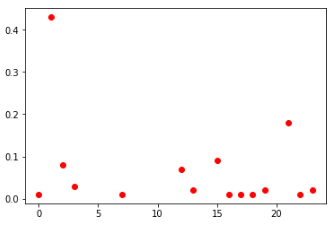deuxième cellule parmi tous les joueurs (à gauche) et TOP-100 (à droite)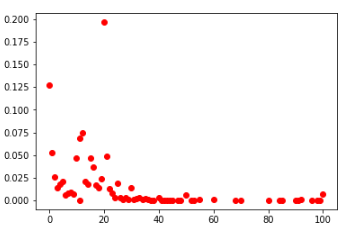
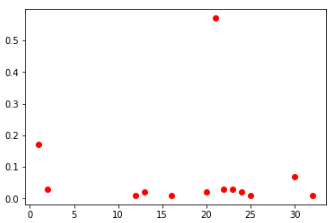cellules centrales entre tous et TOP-100
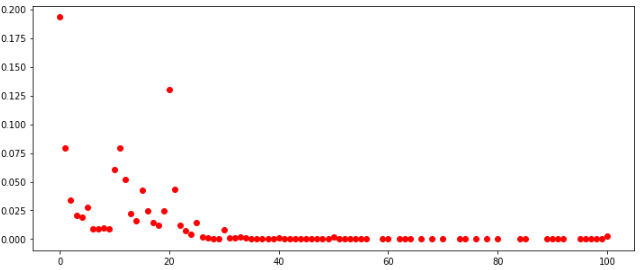répartition des nombres sur tous les jeux
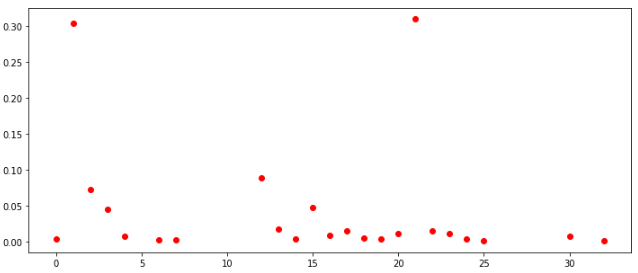répartition des nombres selon TOP-100Si vous regardez la distribution dans toutes les cellules entre tous les joueurs, ils sont généralement similaires. On peut également conclure que dans ces conditions, cela n'a aucun sens de remplir les cellules avec des valeurs supérieures à 30.
C’est là que l’étude prend fin - c’est tout ce que j’ai pu extraire de ces données. Peut-être que l'un d'entre vous pourra proposer autre chose que vous pourrez vérifier - je vous attends dans les commentaires. Recherchez les jeux impersonnels
ici .
Py.Sy. Dans un post précédent, j'ai parlé d'un neurone qui apprenait à jouer à ce jeu. Malheureusement, rien de tout cela n'a encore été réalisé. Deux neurones ont décidé que la meilleure stratégie était de jeter des zéros à la sortie et de profiter du tirage. Mais peut-être que je vais le comprendre à nouveau et faire un article séparé sur les erreurs que j'ai faites lors de la création d'un neurone et, éventuellement, du succès.