Équations différentielles ordinaires neuronales

Une proportion importante de processus est décrite par des équations différentielles, cela peut être l’évolution du système physique dans le temps, l’état de santé du patient, les caractéristiques fondamentales de la bourse, etc. Les données sur ces processus sont de nature cohérente et continue, en ce sens que les observations ne sont que des manifestations d'une sorte d'état en constante évolution.

Il existe également un autre type de données série, ce sont les données discrètes, par exemple les données de tâche PNL. L'état de ces données varie discrètement: d'un caractère ou d'un mot à l'autre.

Désormais, les deux types de ces données série sont généralement traités par des réseaux récursifs, bien qu'ils soient de nature différente et semblent nécessiter des approches différentes.

Un article très intéressant a été présenté lors de la dernière conférence NIPS , qui peut aider à résoudre ce problème. Les auteurs proposent une approche qu'ils ont appelée Neural ODEs .

Ici, j'ai essayé de reproduire et de résumer les résultats de cet article afin de faciliter un peu la connaissance de son idée. Il me semble que cette nouvelle architecture pourrait bien trouver sa place dans les outils standards d'un data scientist aux côtés de réseaux convolutionnels et récurrents.

Figure 1: La rétropropagation à gradient continu nécessite de résoudre l'équation différentielle augmentée dans le temps.

Les flèches représentent l'ajustement des gradients propagés vers l'arrière par les gradients à partir des observations.

Illustration de l'article original.

Énoncé du problème

Qu'il y ait un processus qui obéit à une ODE inconnue et qu'il y ait plusieurs observations (bruyantes) le long de la trajectoire du processus

$\ frac {dz} {dt} = f (z (t), t) \; (1)$

$\ {(z_0, t_0), (z_1, t_1), ..., (z_M, t_M) \} - \ text {observations}$

Comment trouver une approximation $\ widehat {f} (z, t, \ thêta)$ fonctions de haut-parleur f (z, t)

?

Considérons d'abord une tâche plus simple: il n'y a que 2 observations, au début et à la fin de la trajectoire, (z_0, t_0), (z_1, t_1)

.

L'évolution du système commence à partir de l'état z_0, t_0

à l'heure

avec une fonction de dynamique paramétrée utilisant n'importe quelle méthode d'évolution des systèmes ODE. Une fois que le système est dans un nouvel état $\ hat {z_1}, t_1$ , il est comparé à l'état z_1

et la différence entre eux est minimisée en faisant varier les paramètres $\ thêta$ fonctions dynamiques.

Ou, plus formellement, envisagez de minimiser la fonction de perte $L (\ chapeau {z_1})$ :

$L (z (t_1)) = L \ Big (\ int_ {t_0} ^ {t_1} f (z (t), t, \ theta) dt \ Big) = L \ big (\ text {ODESolve} (z ( t_0), f, t_0, t_1, \ theta) \ big) \; (2)$

Pour minimiser

, vous devez calculer les gradients pour tous ses paramètres: $z (t_0), t_0, t_1, \ thêta$ . Pour ce faire, vous devez d'abord déterminer comment

dépend de l'état à chaque instant (z (t))

$a (t) = - \ frac {\ partial L} {\ partial z (t)} \; (3)$

est appelé état adjoint , sa dynamique est donnée par une autre équation différentielle, qui peut être considérée comme un analogue continu de la différenciation d'une fonction complexe ( règle de chaîne ):

$\ frac {d a (t)} {d t} = -a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial z} \; (4)$

Le résultat de cette formule se trouve en annexe de l'article d'origine.

Les vecteurs de cet article doivent être considérés comme des vecteurs en minuscules, bien que l'article d'origine utilise à la fois une représentation en ligne et en colonne.

En résolvant diffur (4) dans le temps, on obtient une dépendance de l'état initial z (t_0)

$\ frac {\ partial L} {\ partial z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial z} dt \; (5)$

Pour calculer le gradient par rapport à

et $\ thêta$ , vous pouvez simplement les considérer comme faisant partie de l'État. Cette condition est appelée augmentée . La dynamique de cet état est obtenue trivialement à partir de la dynamique d'origine:

$\ frac {d} {dt} \ begin {bmatrix} z \\ \ theta \\ t \ end {bmatrix} (t) = f _ {\ text {aug}} ([z, \ theta, t]): = \ begin {bmatrix} f ([z, \ theta, t]) \\ 0 \\ 1 \ end {bmatrix} \; (6)$

Puis l'état conjugué à cet état augmenté:

$a _ {\ text {aug}}: = \ begin {bmatrix} a \\ a _ {\ theta} \\ a_t \ end {bmatrix}, a _ {\ theta} (t): = \ frac {\ partial L} { \ partial \ theta (t)}, a_t (t): = \ frac {\ partial L} {\ partial t (t)} \; (7)$

Dynamique augmentée par gradient:

$\ frac {\ partial f _ {\ text {aug}}} {\ partial [z, \ theta, t]} = \ begin {bmatrix} \ frac {\ partial f} {\ partial z} &; \ frac {\ partial f} {\ partial \ theta} &; \ frac {\ partial f} {\ partial t} \\ 0 &; 0 &; 0 \\ 0 &; 0 &; 0 \ end {bmatrix} \; (8)$

L'équation différentielle de l'état augmenté conjugué de la formule (4) alors:

$\ frac {d a _ {\ text {aug}}} {dt} = - \ begin {bmatrix} a \ frac {\ partial f} {\ partial z} &; a \ frac {\ partial f} {\ partial \ theta} &; a \ frac {\ partial f} {\ partial t} \ end {bmatrix} \; (9)$

Résoudre cette ODE dans le temps donne:

$\ frac {\ partial L} {\ partial z (t_0)} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial z} dt \; (10)$

$\ frac {\ partial L} {\ partial \ theta} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial \ theta } dt \; (11)$

$\ frac {\ partial L} {\ partial t_0} = \ int_ {t_1} ^ {t_0} a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial t} dt \; (12)$

Avec quoi

$\ frac {\ partial L} {\ partial t_1} = - a (t) \ frac {\ partial f (z (t), t, \ theta)} {\ partial t} \; (13)$

donne des dégradés dans tous les paramètres d'entrée au solveur ODESolve ODE.

Tous les gradients (10), (11), (12), (13) peuvent être calculés ensemble dans un appel ODESolve avec la dynamique de l'état augmenté conjugué (9).

Illustration de l'article original.

L'algorithme ci-dessus décrit la propagation inverse du gradient de la solution ODE pour des observations successives.

Dans le cas de plusieurs observations sur une même trajectoire, tout est calculé de la même manière, mais aux moments des observations, l'inverse du gradient propagé doit être ajusté avec des gradients de l'observation courante, comme le montre la figure 1 .

Implémentation

Le code ci-dessous est mon implémentation des ODE neuronaux . Je l'ai fait uniquement pour mieux comprendre ce qui se passe. Cependant, il est très proche de ce qui est implémenté dans le référentiel des auteurs de l'article. Il contient tout le code que vous devez comprendre en un seul endroit, il est également légèrement plus commenté. Pour des applications et expérimentations réelles, il est toujours préférable d'utiliser l'implémentation des auteurs de l'article original.

import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()

Vous devez d'abord implémenter n'importe quelle méthode pour l'évolution des systèmes ODE. Par souci de simplicité, la méthode Euler est implémentée ici, bien que toute méthode explicite ou implicite convienne.

 def ode_solve(z0, t0, t1, f): """     -   """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z

Il décrit également la superclasse d'une fonction de dynamique paramétrée avec quelques méthodes utiles.

Premièrement: vous devez renvoyer tous les paramètres dont dépend la fonction sous la forme d'un vecteur.

Deuxièmement: il est nécessaire de calculer la dynamique augmentée. Cette dynamique dépend du gradient de la fonction paramétrée en termes de paramètres et de données d'entrée. Afin de ne pas avoir à enregistrer le gradient avec chaque main pour chaque nouvelle architecture, nous utiliserons la méthode torch.autograd.grad .

 class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True ) #  grad       , #  expand   if adfdp is not None: adfdp = torch.cat([p_grad.flatten() for p_grad in adfdp]).unsqueeze(0) adfdp = adfdp.expand(batch_size, -1) / batch_size if adfdt is not None: adfdt = adfdt.expand(batch_size, 1) / batch_size return out, adfdz, adfdt, adfdp def flatten_parameters(self): p_shapes = [] flat_parameters = [] for p in self.parameters(): p_shapes.append(p.size()) flat_parameters.append(p.flatten()) return torch.cat(flat_parameters)

Le code ci-dessous décrit la propagation avant et arrière pour les ODE neuronaux . Il est nécessaire de séparer ce code du module torch.nn.Module principal sous la forme de la fonction torch.autograd.Function car dans ce dernier, vous pouvez implémenter une méthode de rétropropagation arbitraire, par opposition à un module. Ce n'est donc qu'une béquille.

Cette fonctionnalité sous-tend toute l'approche Neural ODE .

 class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0) #   , #       def augmented_dynamics(aug_z_i, t_i): """   -     t_i -   : bs, 1 aug_z_i -   : bs, n_dim*2 + n_params + 1 """ #     z_i, a = aug_z_i[:, :n_dim], aug_z_i[:, n_dim:2*n_dim] # Unflatten z and a z_i = z_i.view(bs, *z_shape) a = a.view(bs, *z_shape) with torch.set_grad_enabled(True): t_i = t_i.detach().requires_grad_(True) z_i = z_i.detach().requires_grad_(True) faug = func.forward_with_grad(z_i, t_i, grad_outputs=a) func_eval, adfdz, adfdt, adfdp = faug adfdz = adfdz if adfdz is not None else torch.zeros(bs, *z_shape) adfdp = adfdp if adfdp is not None else torch.zeros(bs, n_params) adfdt = adfdt if adfdt is not None else torch.zeros(bs, 1) adfdz = adfdz.to(z_i) adfdp = adfdp.to(z_i) adfdt = adfdt.to(z_i) # Flatten f and adfdz func_eval = func_eval.view(bs, n_dim) adfdz = adfdz.view(bs, n_dim) return torch.cat((func_eval, -adfdz, -adfdp, -adfdt), dim=1) dLdz = dLdz.view(time_len, bs, n_dim) # flatten dLdz   with torch.no_grad(): ##      #    , #       adj_z = torch.zeros(bs, n_dim).to(dLdz) adj_p = torch.zeros(bs, n_params).to(dLdz) #    z  p,        adj_t = torch.zeros(time_len, bs, 1).to(dLdz) for i_t in range(time_len-1, 0, -1): z_i = z[i_t] t_i = t[i_t] f_i = func(z_i, t_i).view(bs, n_dim) #      dLdz_i = dLdz[i_t] dLdt_i = torch.bmm(torch.transpose(dLdz_i.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #     adj_z += dLdz_i adj_t[i_t] = adj_t[i_t] - dLdt_i #      aug_z = torch.cat(( z_i.view(bs, n_dim), adj_z, torch.zeros(bs, n_params).to(z) adj_t[i_t]), dim=-1 ) #  ()      aug_ans = ode_solve(aug_z, t_i, t[i_t-1], augmented_dynamics) #       adj_z[:] = aug_ans[:, n_dim:2*n_dim] adj_p[:] += aug_ans[:, 2*n_dim:2*n_dim + n_params] adj_t[i_t-1] = aug_ans[:, 2*n_dim + n_params:] del aug_z, aug_ans ##         #    dLdz_0 = dLdz[0] dLdt_0 = torch.bmm(torch.transpose(dLdz_0.unsqueeze(-1), 1, 2), f_i.unsqueeze(-1))[:, 0] #  adj_z += dLdz_0 adj_t[0] = adj_t[0] - dLdt_0 return adj_z.view(bs, *z_shape), adj_t, adj_p, None

Maintenant, pour plus de commodité, encapsulez cette fonction dans nn.Module .

 class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]

Candidature

Récupération de la fonction dynamique réelle (vérification d'approche)

À titre de test de base, vérifions maintenant si Neural ODE peut restaurer la véritable fonction de la dynamique à l'aide de données d'observation.

Pour ce faire, nous déterminons d'abord la fonction dynamique de l'ODE, faisons évoluer la trajectoire en fonction de celle-ci, puis essayons de la restaurer à partir de la fonction dynamique paramétrée au hasard.

Tout d'abord, examinons le cas le plus simple d'une ODE linéaire. La fonction dynamique n'est que l'action d'une matrice.

$\ frac {dz} {dt} = \ begin {bmatrix} -0.1 &; -1,0 \\ 1,0 &; -0,1 \ end {bmatrix} z$

La fonction entraînée est paramétrée par une matrice aléatoire.

De plus, une dynamique un peu plus sophistiquée (sans gif, car le processus d'apprentissage n'est pas si beau :))
La fonction d'apprentissage ici est un réseau entièrement connecté avec une couche cachée.

Code

 class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)

La fonction dynamique n'est qu'une matrice

 class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)

Matrice paramétrée au hasard

 class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)

Dynamique pour des trajectoires plus sophistiquées

 class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt

Dynamique d'apprentissage sous la forme d'un réseau entièrement connecté

 class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10): # Create data z0 = Variable(torch.Tensor([[0.6, 0.3]])) t_max = 6.29*5 n_points = 200 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]]) times = torch.from_numpy(times_np[:, :, None]).to(z0) obs = ode_true(z0, times, return_whole_sequence=True).detach() obs = obs + torch.randn_like(obs) * 0.01 # Get trajectory of random timespan min_delta_time = 1.0 max_delta_time = 5.0 max_points_num = 32 def create_batch(): t0 = np.random.uniform(0, t_max - max_delta_time) t1 = t0 + np.random.uniform(min_delta_time, max_delta_time) idx = sorted(np.random.permutation( index_np[(times_np > t0) & (times_np < t1)] )[:max_points_num]) obs_ = obs[idx] ts_ = times[idx] return obs_, ts_ # Train Neural ODE optimizer = torch.optim.Adam(ode_trained.parameters(), lr=0.01) for i in range(n_steps): obs_, ts_ = create_batch() z_ = ode_trained(obs_[0], ts_, return_whole_sequence=True) loss = F.mse_loss(z_, obs_.detach()) optimizer.zero_grad() loss.backward(retain_graph=True) optimizer.step() if i % plot_freq == 0: z_p = ode_trained(z0, times, return_whole_sequence=True) plot_trajectories(obs=[obs], times=[times], trajs=[z_p], save=f"assets/imgs/{name}/{i}.png") clear_output(wait=True) ode_true = NeuralODE(SpiralFunctionExample()) ode_trained = NeuralODE(RandomLinearODEF()) conduct_experiment(ode_true, ode_trained, 500, "linear") func = TestODEF(Tensor([[-0.1, -0.5], [0.5, -0.1]]), Tensor([[0.2, 1.], [-1, 0.2]]), Tensor([[-1., 0.]])) ode_true = NeuralODE(func) func = NNODEF(2, 16, time_invariant=True) ode_trained = NeuralODE(func) conduct_experiment(ode_true, ode_trained, 3000, "comp", plot_freq=30)

Comme vous pouvez le voir, Neural ODE fait un très bon travail de restauration de la dynamique. Autrement dit, le concept dans son ensemble fonctionne.
Maintenant, vérifiez un problème légèrement plus compliqué (MNIST, haha).

Neural ODE inspiré par ResNets

Dans ResNet'ax, l'état latent change selon la formule

$h_ {t + 1} = h_ {t} + f (h_ {t}, \ theta_ {t})$

où $t \ in \ {0 ... T \}$ Est le numéro de bloc et

c'est une fonction apprise par les couches à l'intérieur du bloc.

À la limite, si nous prenons un nombre infini de blocs avec des pas toujours plus petits, nous obtenons la dynamique continue de la couche cachée sous la forme d'un ODE, tout comme ce qui était ci-dessus.

$\ frac {dh (t)} {dt} = f (h (t), t, \ theta)$

À partir de la couche d'entrée h (0)

nous pouvons définir la couche de sortie h (T)

comme solution à cette ODE au temps T.

Maintenant on peut compter $\ thêta$ en tant que paramètres distribués ( partagés ) entre tous les blocs infinitésimaux.

Validation de l'architecture Neural ODE sur MNIST

Dans cette partie, nous allons tester la capacité de Neural ODE à être utilisé comme composants dans des architectures plus familières.

En particulier, nous remplacerons les blocs résiduels par Neural ODE dans le classificateur MNIST.

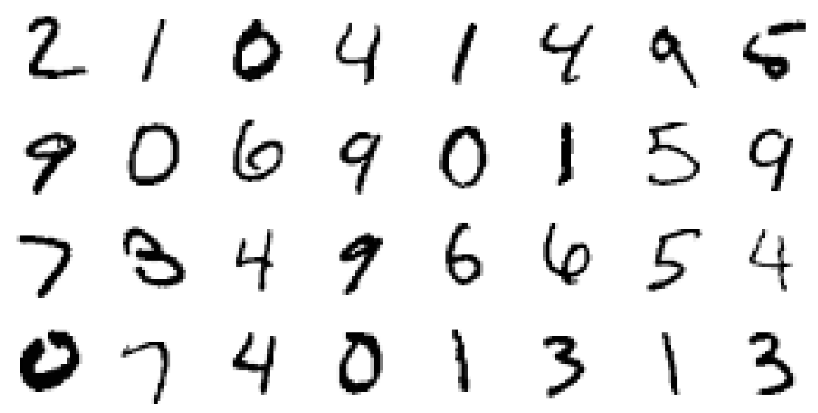
Code

 def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")

 Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%

Après un entraînement très rude en seulement 5 époques et 6 minutes d'entraînement, le modèle a déjà atteint une erreur de test de moins de 1%. Nous pouvons dire que les ODE neuronaux s'intègrent bien en tant que composant dans des réseaux plus traditionnels.

Dans leur article, les auteurs comparent également ce classificateur (ODE-Net) avec un réseau régulier entièrement connecté, avec ResNet avec une architecture similaire, et avec exactement la même architecture, dans laquelle le gradient se propage directement via les opérations dans ODESolve (sans la méthode du gradient conjugué) ( RK-Net).

Illustration de l'article original.

Selon eux, un réseau à une couche entièrement connecté avec environ le même nombre de paramètres que Neural ODE a une erreur beaucoup plus élevée sur le test, ResNet avec à peu près la même erreur a beaucoup plus de paramètres et RK-Net sans la méthode du gradient conjugué a une erreur légèrement plus élevée et avec une consommation de mémoire augmentant linéairement (plus l'erreur tolérée est petite, plus ODESolve doit faire de pas, ce qui augmente linéairement la consommation de mémoire avec le nombre de pas).

Les auteurs utilisent la méthode implicite Runge-Kutta avec une taille de pas adaptative dans leur implémentation, contrairement à la méthode Euler plus simple ici. Ils étudient également certaines propriétés de la nouvelle architecture.

Fonction ODE-Net (NFE Forward - le nombre de calculs de fonction dans un passage direct)
Illustration de l'article original.

(a) La modification du niveau acceptable d'erreur numérique modifie le nombre d'étapes de la distribution directe.
(b) Le temps consacré à la distribution directe est proportionnel au nombre de calculs de la fonction.
(c) Le nombre de calculs de la fonction de rétropropagation représente environ la moitié de la propagation directe, ce qui indique que la méthode du gradient conjugué peut être plus efficace sur le plan du calcul que la propagation du gradient directement via ODESolve .
(d) Comme ODE-Net devient de plus en plus entraîné, il nécessite de plus en plus de calculs d'une fonction (une étape toujours plus petite), s'adaptant éventuellement à la complexité croissante du modèle.

Fonction générative cachée pour la modélisation de séries chronologiques

Neural ODE convient au traitement de données en série continues même lorsque le chemin se trouve dans un espace caché inconnu.

Dans cette section, nous allons expérimenter et modifier la génération de séquences continues à l'aide de Neural ODE , et jeter un œil à l'espace caché appris.

Les auteurs comparent également cela avec des séquences similaires générées par des réseaux récurrents.

L'expérience ici est légèrement différente de l'exemple correspondant dans le référentiel des auteurs, ici il y a un ensemble plus diversifié de chemins.

Les données

Les données d'entraînement sont constituées de spirales aléatoires, dont la moitié dans le sens horaire et la seconde dans le sens antihoraire. Des sous-séquences aléatoires sont ensuite échantillonnées à partir de ces spirales, traitées par le modèle récursif de codage dans la direction opposée, générant un état caché de départ, qui évolue ensuite, créant une trajectoire dans l'espace caché. Ce chemin latent est ensuite mappé à l'espace de données et comparé à la sous-séquence échantillonnée. Ainsi, le modèle apprend à générer des trajectoires similaires à un ensemble de données.

Exemples de spirales d'ensembles de données

La VAE comme modèle génératif

Modèle génératif par une procédure d'échantillonnage:

$z_ {t_0} \ sim \ mathcal {N} (0, I)$

$z_ {t_1}, z_ {t_2}, ..., z_ {t_M} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_M)$

$x_ {t_i} \ sim p (x \ mid z_ {t_i}; \ theta_x)$

Qui peut être formé en utilisant l'approche auto-encodeur variationnel.

Parcourez un encodeur récurrent à travers une séquence temporelle dans le temps pour obtenir les paramètres $\ mu_ {z_ {t_0}}$ , $\ sigma_ {z_ {t_0}}$ distribution variationnelle postérieure, puis en échantillonner:

$z_ {t_0} \ sim q \ left (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q \ right) = \ mathcal {N} \ gauche (z_ {t_0} \ mid \ mu_ {z_ {t_0}} \ sigma_ {z_ {t_0}} \ right)$

Obtenez une trajectoire cachée:

$z_ {t_1}, z_ {t_2}, ..., z_ {t_N} = \ text {ODESolve} (z_ {t_0}, f, \ theta_f, t_0, ..., t_N), \ text {where} \ frac {dz} {dt} = f (z, t; \ theta_f)$

Mappez un chemin caché sur un chemin dans les données à l'aide d'un autre réseau de neurones: $\ hat {x_ {t_i}} (z_ {t_i}, t_i; \ theta_x)$
Maximisez l'évaluation de la limite inférieure de validité (ELBO) pour le chemin échantillonné:

$\ text {ELBO} \ approx N \ Big (\ sum_ {i = 0} ^ {M} \ log p (x_ {t_i} \ mid z_ {t_i} (z_ {t_0}; \ theta_f); \ theta_x) + KL \ left (q (z_ {t_0} \ mid x_ {t_0}, ..., x_ {t_M}; t_0, ..., t_M; \ theta_q) \ parallel \ mathcal {N} (0, I) \ à droite) \ Big)$

Et dans le cas d'une distribution postérieure gaussienne $p (x \ mid z_ {t_i}; \ theta_x)$ et niveau de bruit connu $\ sigma_x$ :

$\ text {ELBO} \ approx -N \ Big (\ sum_ {i = 1} ^ {M} \ frac {(x_i - \ hat {x_i}) ^ 2} {\ sigma_x ^ 2} - \ log \ sigma_ { z_ {t_0}} ^ 2 + \ mu_ {z_ {t_0}} ^ 2 + \ sigma_ {z_ {t_0}} ^ 2 \ Big) + C$

Le graphique de calcul d'un modèle ODE masqué peut être représenté comme suit

Illustration de l'article original.

Ce modèle peut ensuite être testé pour savoir comment il interpole le chemin en utilisant uniquement les observations initiales.

Code

Définir des modèles

 class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t): # Concatenate time to input t = t.clone() t[1:] = t[:-1] - t[1:] t[0] = 0. xt = torch.cat((x, t), dim=-1) _, h0 = self.rnn(xt.flip((0,))) # Reversed # Compute latent dimension z0 = self.hid2lat(h0[0]) z0_mean = z0[:, :self.latent_dim] z0_log_var = z0[:, self.latent_dim:] return z0_mean, z0_log_var class NeuralODEDecoder(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(NeuralODEDecoder, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim func = NNODEF(latent_dim, hidden_dim, time_invariant=True) self.ode = NeuralODE(func) self.l2h = nn.Linear(latent_dim, hidden_dim) self.h2o = nn.Linear(hidden_dim, output_dim) def forward(self, z0, t): zs = self.ode(z0, t, return_whole_sequence=True) hs = self.l2h(zs) xs = self.h2o(hs) return xs class ODEVAE(nn.Module): def __init__(self, output_dim, hidden_dim, latent_dim): super(ODEVAE, self).__init__() self.output_dim = output_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.encoder = RNNEncoder(output_dim, hidden_dim, latent_dim) self.decoder = NeuralODEDecoder(output_dim, hidden_dim, latent_dim) def forward(self, x, t, MAP=False): z_mean, z_log_var = self.encoder(x, t) if MAP: z = z_mean else: z = z_mean + torch.randn_like(z_mean) * torch.exp(0.5 * z_log_var) x_p = self.decoder(z, t) return x_p, z, z_mean, z_log_var def generate_with_seed(self, seed_x, t): seed_t_len = seed_x.shape[0] z_mean, z_log_var = self.encoder(seed_x, t[:seed_t_len]) x_p = self.decoder(z_mean, t) return x_p

Génération de jeux de données

 t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32) # Generate random spirals parameters normal01 = torch.distributions.Normal(0, 1.0) x0 = Variable(normal01.sample((num_spirals, 2))) * 2.0 W11 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W22 = -0.1 * normal01.sample((num_spirals,)).abs() - 0.05 W21 = -1.0 * normal01.sample((num_spirals,)).abs() W12 = 1.0 * normal01.sample((num_spirals,)).abs() xs_list = [] for i in range(num_spirals): if i % 2 == 1: # Make it counter-clockwise W21, W12 = W12, W21 func = LinearODEF(Tensor([[W11[i], W12[i]], [W21[i], W22[i]]])) ode = NeuralODE(func) xs = ode(x0[i:i+1], times[:, i:i+1], return_whole_sequence=True) xs_list.append(xs) orig_trajs = torch.cat(xs_list, dim=1).detach() samp_trajs = orig_trajs + torch.randn_like(orig_trajs) * noise_std samp_ts = times fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(samp_trajs[:, i, 0], samp_trajs[:, i, 1], c=samp_ts[:, i, 0], cmap=cm.plasma) plt.show() import numpy.random as npr def gen_batch(batch_size, n_sample=100): n_batches = samp_trajs.shape[1] // batch_size time_len = samp_trajs.shape[0] n_sample = min(n_sample, time_len) for i in range(n_batches): if n_sample > 0: probs = [1. / (time_len - n_sample)] * (time_len - n_sample) t0_idx = npr.multinomial(1, probs) t0_idx = np.argmax(t0_idx) tM_idx = t0_idx + n_sample else: t0_idx = 0 tM_idx = time_len frm, to = batch_size*i, batch_size*(i+1) yield samp_trajs[t0_idx:tM_idx, frm:to], samp_ts[t0_idx:tM_idx, frm:to]

La formation

 vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")

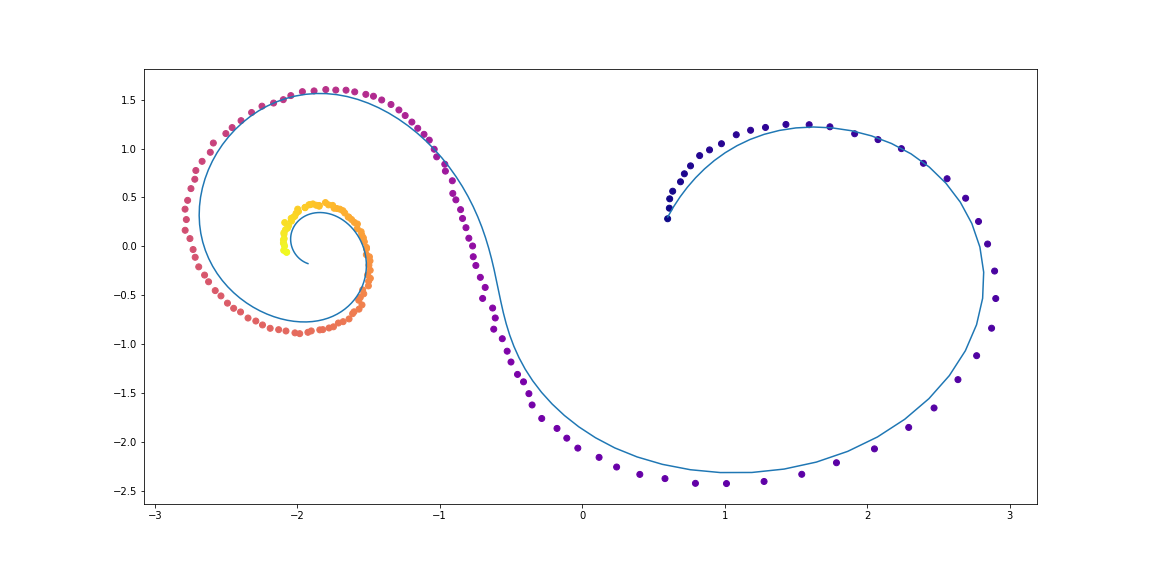
Voilà ce qui se passe après une nuit d'entraînement

Les points sont des observations bruyantes de la trajectoire d'origine (bleu), le
jaune sont des trajectoires reconstruites et interpolées, en utilisant des points comme entrées.

La couleur du point indique le temps.

Les reconstitutions de certains exemples ne semblent pas trop bonnes. Peut-être que le modèle n'est pas assez complexe ou pas étudié assez longtemps. En tout cas, la reconstruction semble très raisonnable.

Voyons maintenant ce qui se passe si nous interpolons une variable cachée dans le sens horaire vers un chemin anti-horloge.

Les auteurs comparent également les reconstructions et les interpolations de chemin entre Neural ODE et un simple réseau récursif.

Illustration de l'article original.

Flux de normalisation continus

L'article original apporte également beaucoup au sujet de la normalisation des flux. Les flux de normalisation sont utilisés lorsque vous devez échantillonner à partir d'une distribution complexe qui apparaît à travers le changement de variables à partir d'une distribution simple (gaussienne, par exemple), et que vous connaissez toujours la densité de probabilité au point de chaque échantillon.
Les auteurs montrent que l'utilisation de la substitution de variable continue est beaucoup plus efficace sur le plan informatique et interprétable que les méthodes précédentes.

Les flux de normalisation sont très utiles dans des modèles tels que les codeurs automatiques de variation , les réseaux neuronaux bayésiens et d'autres de l'approche bayésienne.

Ce sujet, cependant, sort du cadre de cettearticles, et ceux qui sont intéressés devraient lire l'article scientifique original.

Pour les semences:

Visualisation de la transformation du bruit (distribution simple) en données (distribution complexe) pour deux jeux de données;

L'axe des X montre la transformation de la densité et des échantillons au cours du «temps» (pour NS) et de la «profondeur» (pour NS).

Illustration de l'article original

Merci à bekemax pour son aide dans l'édition de la version anglaise du texte et pour ses commentaires physiques intéressants.

Ceci conclut ma petite recherche sur les ODE neuronales . Merci de votre attention!

Présentation de Neural ODE

Équations différentielles ordinaires neuronales

Énoncé du problème

Implémentation

Candidature

Récupération de la fonction dynamique réelle (vérification d'approche)

Neural ODE inspiré par ResNets

Validation de l'architecture Neural ODE sur MNIST

Fonction générative cachée pour la modélisation de séries chronologiques

Les données

La VAE comme modèle génératif

Définir des modèles

Génération de jeux de données

La formation

Flux de normalisation continus

Liens utiles

More articles: