Mise en cluster des points d'accès sans fil à l'aide de la méthode k-means

La visualisation et l'analyse des données sont actuellement largement utilisées dans l'industrie des télécommunications. En particulier, l'analyse dépend fortement de l'utilisation de données géospatiales. Cela est peut-être dû au fait que les réseaux de télécommunications eux-mêmes sont géographiquement dispersés. En conséquence, l'analyse de telles dispersions peut être extrêmement utile.

Les données

Pour illustrer l'algorithme de clustering k-means, nous utiliserons la base de données géographiques pour le WiFi public gratuit à New York. L'ensemble de données est disponible sur NYC Open Data. En particulier, l'algorithme de clustering k-means est utilisé pour former des clusters d'utilisation du WiFi basés sur des données de latitude et de longitude.

Les données de latitude et de longitude sont extraites de l'ensemble de données lui-même à l'aide du langage de programmation R:

#1. Prepare data newyork<-read.csv("NYC_Free_Public_WiFi_03292017.csv") attach(newyork) newyorkdf<-data.frame(newyork$LAT,newyork$LON) 

Voici un morceau de données:

Nous déterminons le nombre de clusters

Ensuite, nous déterminons le nombre de clusters en utilisant le code ci-dessous, qui montre le résultat dans un graphique.

 #2. Determine number of clusters wss <- (nrow(newyorkdf)-1)*sum(apply(newyorkdf,2,var)) for (i in 2:20) wss[i] <- sum(kmeans(newyorkdf, centers=i)$withinss) plot(1:20, wss, type="b", xlab="Number of Clusters", ylab="Within groups sum of squares") 

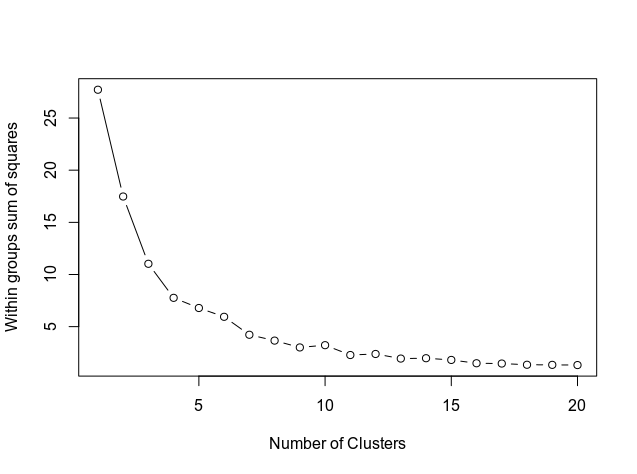
Le graphique montre comment la courbe s'aligne aux alentours de 11. Par conséquent, il s'agit du nombre de grappes qui seront utilisées dans le modèle k-means.

Analyse K-means

L'analyse des K-means est effectuée:

 #3. K-Means Cluster Analysis set.seed(20) fit <- kmeans(newyorkdf, 11) # 11 cluster solution # get cluster means aggregate(newyorkdf,by=list(fit$cluster),FUN=mean) # append cluster assignment newyorkdf <- data.frame(newyorkdf, fit$cluster) newyorkdf newyorkdf$fit.cluster <- as.factor(newyorkdf$fit.cluster) library(ggplot2) ggplot(newyorkdf, aes(x=newyork.LON, y=newyork.LAT, color = newyorkdf$fit.cluster)) + geom_point() 

Le jeu de données newyorkdf contient des informations sur la latitude, la longitude et l'étiquette du cluster:
> newyorkdf
newyork.lat newyork.lon fit.cluster
1 40,75573 -73,94458 1
2 40,75533 -73,94413 1
3 40,75575 -73,94517 1
4 40,75575 -73,94517 1
5 40,75575 -73,94517 1
6 40,75575 -73,94517 1
...
80 40,84832 -73,82075 11

En voici une illustration claire:



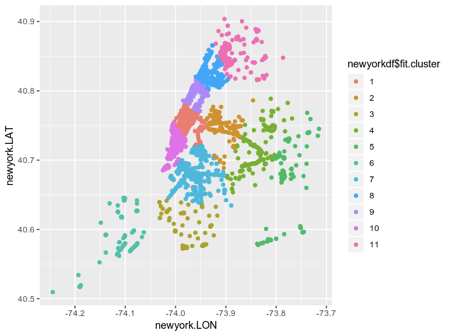
Cette illustration est utile, mais la visualisation sera encore plus précieuse si vous la superposez sur une carte de New York elle-même.

 # devtools::install_github("zachcp/nycmaps") library(nycmaps) map(database="nyc") #this should also work with ggplot and ggalt nyc <- map_data("nyc") gg <- ggplot() gg <- gg + geom_map( data=nyc, map=nyc, aes(x=long, y=lat, map_id=region)) gg + geom_point(data = newyorkdf, aes(x = newyork.LON, y = newyork.LAT), colour = newyorkdf$fit.cluster, alpha = .5) + ggtitle("New York Public WiFi") 

Ce type de clustering donne une excellente idée de la structure d'un réseau WiFi dans une ville. Cela indique que la région géographique marquée par le cluster 1 montre beaucoup de trafic WiFi. En revanche, moins de connexions dans le cluster 6 peuvent indiquer un faible trafic WiFi.

Le clustering K-Means seul ne nous dit pas pourquoi le trafic pour un cluster particulier est élevé ou faible. Par exemple, lorsque le cluster 6 a une densité de population élevée, mais que les faibles vitesses Internet entraînent moins de connexions.

Cependant, cet algorithme de clustering fournit un excellent point de départ pour une analyse plus approfondie et facilite la collecte d'informations supplémentaires. Par exemple, en utilisant cette carte comme exemple, vous pouvez construire des hypothèses concernant des clusters géographiques individuels. L'article original est ici .