Tâches du manuel scolaire II

Partie I
Partie II
Partie III

Cet article décrit la méthode d'estimation de la plage de valeurs acceptées et la relation de cette méthode avec les tâches contenant un module.

Lors de la résolution de certains problèmes, il est nécessaire de considérer la plage dans laquelle la valeur souhaitée peut être.

Considérez la méthode d'estimation pour résoudre les inégalités.

Supposons que le prix par unité de marchandise puisse varier de 5 à 10 RUB. Donner une limite supérieure signifie déterminer la valeur maximale que la quantité souhaitée peut prendre. Pour deux unités de biens dont le prix n'excède pas 10, l'estimation supérieure sera 10 + 10 = 20 .

Considérez le problème à partir du profil de profil de problème MI Bashmakova
37. Estimations connues des variables $$$x$ et$$ $ inline $ y: 0 <x <5, 2 <y <3. $ inline $

Donnez les meilleures notes aux expressions suivantes:
1. $$
2. $$$xy$

5. $$$\ frac {1} {y}$
6. $$$\ frac {x} {y}$

8. $$$x-y$
9. $$$3x-2y$


En général, l'analyse des quantités infinitésimales utilise un critère d'évaluation. Un module (en tant que voisinage) trouve application dans la définition d'une limite.

$$$$ afficher $$ \ gauche | x_ {n} -a \ droite | <\ varepsilon $$ afficher $$

Prenons l'exemple du "Cours du calcul différentiel et intégral" 363 (6)

Divergence de ligne facile à régler

$$

$$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$$

En fait, puisque ses membres diminuent, la nième somme partielle

$$$$ afficher $$ 1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $$ afficher $$

et grandit à l'infini avec $$$n$ .

Afin de prouver que $$$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ vraiment plus $$$\ sqrt {n}$ , vous devez faire une estimation inférieure de cette expression. On obtient le système des inégalités

$$$$ afficher $$ \ left \ {\! \ begin {aligné} & \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & \ frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {aligné} \ à droite. $$ afficher $$

Après avoir ajouté toutes les inégalités de ce système, nous obtenons

$$$$ afficher $$ 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} $$ display $$

C'est la preuve que cette série diverge.

Pour une série harmonique, cette méthode ne fonctionne pas, car $$$n$ série harmonique partielle partielle

$$$$ afficher $$ 1+ \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $$ affichage $$

Retour à la tâche

38. Calculez le montant ("Tâches pour les enfants de 5 à 15 ans")

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ cdot100}$$

(avec une erreur ne dépassant pas 1% de la réponse)

Meilleure estimation de la série $$$\ frac {n} {n + 1}$ donne le numéro 1.

Abandonnez le premier mandat $$$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) 

Nous obtenons $$$1 - \ frac {1} {1 \ cdot2} = \ frac {1} {2}$
0,4166666666666666363
0,49019607843137253
0,4990019960079833
0.4999000199960005
0,49999000019998724
0,4999990000019941

Vous pouvez vérifier sur ideone.com ici


Abandonnez les deux premiers termes $$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) 

Nous obtiendrons 0.33333233333632745
Les sommes partielles de la série sont délimitées ci-dessus.

La ligne positive a toujours un montant; cette somme sera finie (et donc la série convergente) si les sommes partielles de la série sont bornées ci-dessus, et infinie (et la série divergente) sinon.

Jeter $$$n$ termes initiaux de la série harmonique.
Prouver (en utilisant la borne inférieure) que

$$$$ afficher $$ \ frac {1} {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $$ afficher $$

Si, à l'exception des deux premiers termes, les membres restants de la série harmonique sont divisés en groupes par $$ membres dans chaque

$$

$$\ frac {1} {3} + \ frac {1} {4}; \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}; \ frac {1} {9} + ... \ frac {1} {16}; ...;$$

$$

$$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {k}}; ...,$$

alors chacun de ces montants individuellement sera plus grand $$$\ frac {1} {2}$ .
... On voit que des sommes partielles ne peuvent pas être bornées dessus: la série a une somme infinie.

Nous calculons les montants partiels qui sont obtenus en jetant $$$2 ^ {k}$ termes.

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) 

Nous obtenons:
0,583333333333333434
0,6345238095238095
0,6628718503718504
Nous écrivons un programme qui calcule la somme des séries harmoniques à partir de $$$\ frac {n} {2}$ avant $$$n$ où $$$n = 2 ^ {k}$ à $$$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) 

Nous obtenons:
0,583333333333333333
0,6345238095238095
0,6628718503718504
0,6777662022075267

Vous pouvez vous enregistrer en ligne sur le lien
Pour la gamme $$$\ left [1 + 2 ^ {70}; 2 ^ {71} \ right]$ nous obtenons 0,693147 ...
Vérifiez mojo dans Wolfram Cloud ici .

Cet algorithme récursif provoque un débordement de pile rapide.
Cet article présente un exemple de calcul factoriel à l'aide d'un algorithme itératif. Nous modifions cet algorithme itératif pour qu'il calcule la somme partielle Hn dans certaines limites; appeler ces limites a et b

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) 

La borne inférieure est le nombre $$$1 + 2 ^ {k}$ , la limite supérieure est le nombre $$$2 \ cdot 2 ^ {k}$
Nous écrivons une fonction qui calcule la puissance de deux

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) 

Nous substituerons (+ 1 (power_of_two k)) comme limite inférieure et utiliserons la fonction (* 2 (power_of_two k)) ou sa fonction équivalente (power_of_two (+ 1 k)) comme limite supérieure
Réécrire la fonction Hn

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) 

Vous pouvez maintenant calculer Hn pour les grandes valeurs $$$k$ .

Nous écrivons en C un programme qui mesure le temps nécessaire au calcul de Hn . Nous utiliserons la fonction clock () de la bibliothèque standard <time.h>
Un article sur la mesure du temps processeur est sur Habré ici .

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; } 

En général, l'ide en ligne limite le temps d'exécution des programmes en cours d'exécution à cinq secondes, de sorte que ce programme ne peut être vérifié que dans certaines idées en ligne, par exemple, en ligne sur gdb.com ou repl.it
Pour k de 1 + 2 ^ 30 à 2 ^ 31, le temps de fonctionnement sera de ~ 5 sec.
Pour k de 1 + 2 ^ 31 à 2 ^ 32, le temps de fonctionnement sera de ~ 10 sec.
Pour k de 1 + 2 ^ 32 à 2 ^ 33, le temps de fonctionnement sera de ~ 20 sec.
Pour k de 1 + 2 ^ 33 à 2 ^ 34, le temps de fonctionnement sera de ~ 40 sec.
Pour k de 1 + 2 ^ 34 à 2 ^ 35, la durée de fonctionnement sera supérieure à une minute.
...
Pour k de 1 + 2 ^ 45 à 2 ^ 46, la durée de fonctionnement sera supérieure à 24 heures.

Supposons que pour k de 1 + 2 ^ 30 à 2 ^ 31, le temps d'exécution de l'algorithme soit ~ 2 sec.
Alors pour k = 2 ^ (30 + n) le temps d'exécution de l'algorithme est de 2 ^ n sec. (à $$$n \ in \ mathbb {N}$ )
Cet algorithme a une complexité exponentielle .

Retour aux modules.
En calcul intégral, le module est utilisé dans la formule

$$

$$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ left | x \ droite | + C$$

Sur Habré il y avait un article Le logarithme le plus naturel dans lequel cette intégrale est considérée et sur la base de son calcul de nombre $$$e$ .

La présence du module dans la formule $$$\ int \ frac {dx} {x} = ln \ left | x \ droite | + C$ étayé par le "Cours du calcul différentiel et intégral"

Si ...$$ $ en ligne $ x <0 $ en ligne $ , puis par différenciation, il est facile de vérifier que $$$\ left [ln (-x) \ right] '= \ frac {1} {x}$

Application physique de l'intégrale $$$\ int \ frac {dx} {x}$

Cette intégrale est utilisée pour calculer la différence de potentiel des plaques d'un condensateur cylindrique.


"Électricité et magnétisme":

La différence de potentiel entre les plaques se trouve par intégration:

$$

$$\ varphi_ {1} - \ varphi_ {2} = \ int \ limits_ {R_ {1}} ^ {R_ {2}} E (r) dr = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} \ int \ limits_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ {0} \ varepsilon l} ln \ frac {R_ {2}} {R_ {1}}$$

( $$$R_ {1}$ et $$$R_ {2}$ - les rayons des plaques intérieure et extérieure).

Le signe du module n'est pas utilisé ici sous le signe du logarithme naturel $$$ln \ left | \ frac {R_ {2}} {R_ {1}} \ droite |$ parce que $$$R_ {1}$ et $$$R_ {2}$ strictement positif et cette forme d'enregistrement est redondante.

Dessin "modulaire"

À l'aide de modules, vous pouvez dessiner différentes formes.

Si dans le programme geogebra , écrivez la formule $$$abs (x) + abs (y) = 1$ nous obtenons



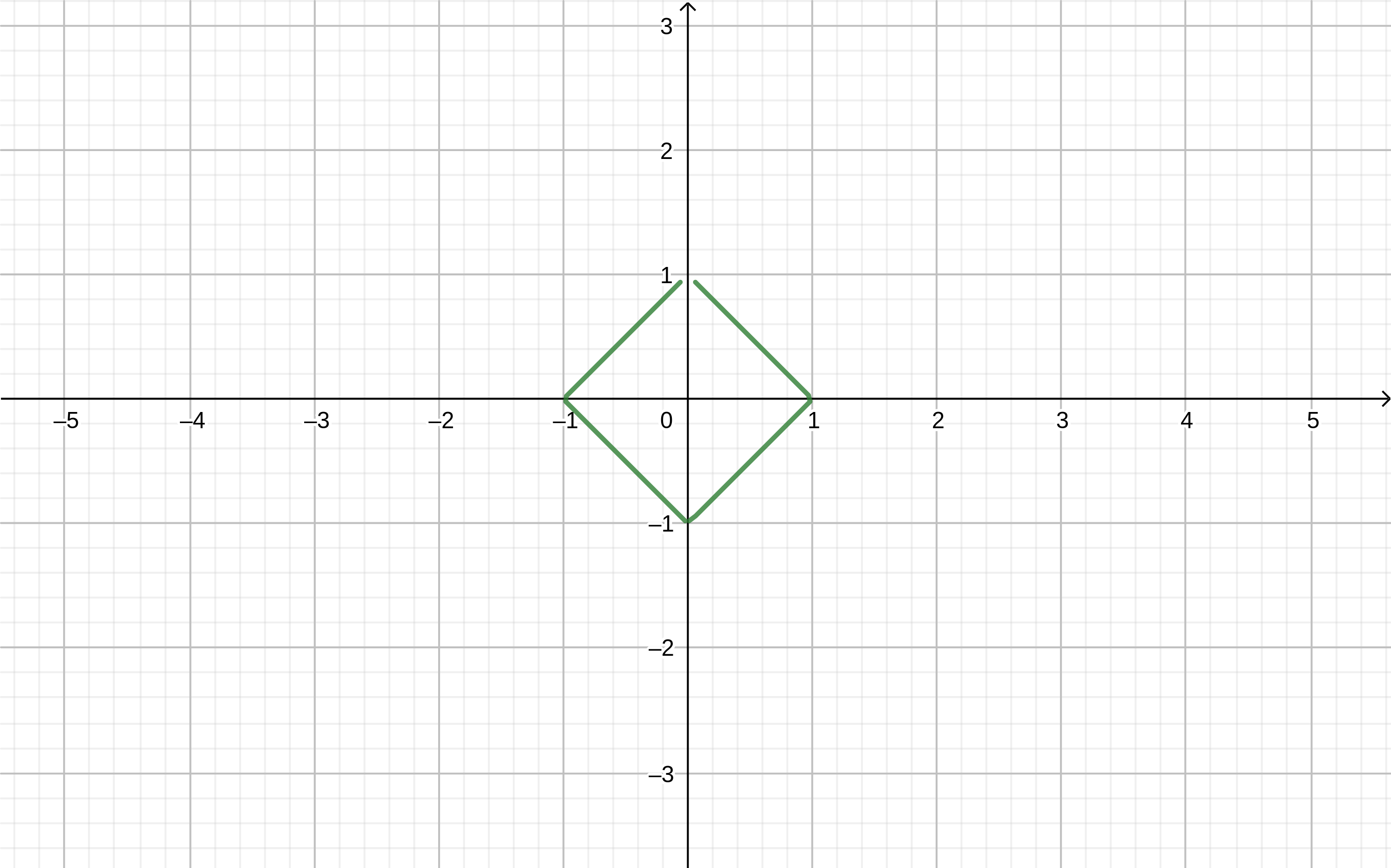
Vous pouvez dessiner des formes plus complexes. Par exemple, dessinons un «papillon» dans le nuage WolframAlpha

$$

$$\ sum \ frac {\ left | x \ droite | } {n- \ left | x \ droite | } + \ frac {\ left | x + n \ droite | } {n} + \ frac {\ left | x-n \ droite | } {n}$$

Tracé [somme [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1,20}], {x, -60,60}]
Dans cette expression $$$n$ se situe dans la gamme de $$$1$ avant $$ , $$$x$ se situe dans la gamme de $$$-60$ avant $$ .
Lien vers l'image.

Livres:

«Le livre de tâches de l'orientation des profils» M.I. Bashmakov
Cours de physique générale: en 3 volumes T. 2. "Electricité et magnétisme" I.V. Savelyev