Bonjour, Habr! J'attire votre attention sur une traduction de l'article de Rudy Gilman et Katherine Wang Intuitive RL: Intro to Advantage-Actor-Critic (A2C) .

Les spécialistes de l'apprentissage renforcé (RL) ont produit de nombreux excellents didacticiels. Cependant, la plupart décrivent RL en termes d'équations mathématiques et de diagrammes abstraits. Nous aimons penser le sujet sous un angle différent. Le RL lui-même est inspiré par la façon dont les animaux apprennent, alors pourquoi ne pas traduire le mécanisme RL sous-jacent en phénomènes naturels qu'il est censé simuler? Les gens apprennent mieux à travers des histoires.
C'est l'histoire du modèle Actor Advantage Critic (A2C). Le modèle sujet-critique est une forme populaire du modèle Policy Gradient, qui est en soi un algorithme RL traditionnel. Si vous comprenez A2C, vous comprenez RL profond.
Après avoir acquis une compréhension intuitive d'A2C, vérifiez:
Illustrations @embermarke
Dans RL, l'agent, le renard Klyukovka, traverse des états entourés d'actions, essayant de maximiser les récompenses en cours de route.
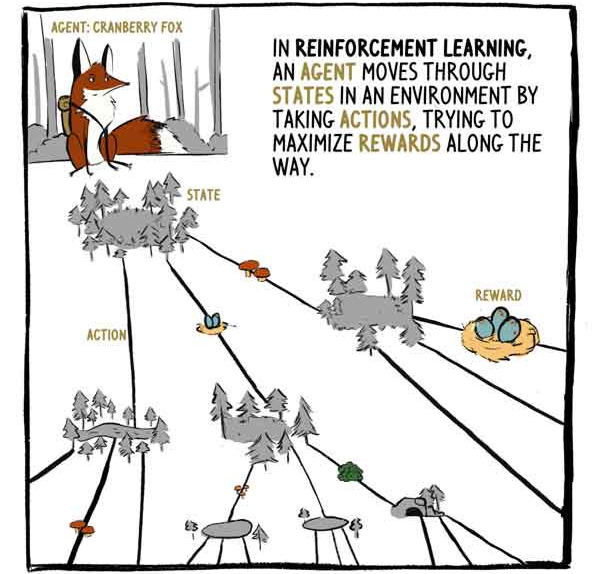
L'A2C reçoit des entrées d'état - entrées de capteur dans le cas de Klukovka - et génère deux sorties:
1) Une évaluation du montant de la récompense qui sera reçue, à partir du moment de l'état actuel, à l'exception de la récompense actuelle (existante).
2) Une recommandation sur les mesures à prendre (politique).
Critique: wow, quelle magnifique vallée! Ce sera une journée fructueuse pour la recherche de nourriture! Je parie aujourd'hui que je collecterai 20 points avant le coucher du soleil.
"Sujet": ces fleurs sont magnifiques, j'ai envie de "A".

Les modèles Deep RL sont des machines de mappage entrée-sortie, comme tout autre modèle de classification ou de régression. Au lieu de catégoriser les images ou le texte, les modèles RL profonds amènent les états aux actions et / ou les états aux valeurs des états. A2C fait les deux.


Cet ensemble de récompense état-action est une observation. Elle écrira cette ligne de données dans son journal, mais elle n'y réfléchira pas encore. Elle le remplira quand elle s'arrêtera pour réfléchir.
Certains auteurs associent la récompense 1 au pas de temps 1, d'autres l'associent à l'étape 2, mais tous ont en tête le même concept: la récompense est associée à l'état, et l'action la précède immédiatement.

Le raccordement répète à nouveau le processus. Tout d'abord, elle perçoit son environnement et développe une fonction V (S) et une recommandation d'action.
Critique: Cette vallée semble assez standard. V (S) = 19.
Objet: Les options d'action semblent très similaires. Je pense que je vais juste aller sur la piste "C".
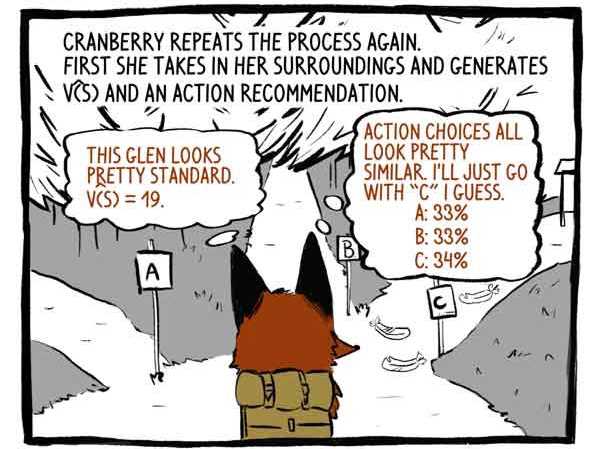
Ensuite, il agit.

Reçoit une récompense de +20! Et enregistre l'observation.

Elle recommence le processus.

Après avoir recueilli trois observations, Klyukovka s'arrête pour réfléchir.
D'autres familles de modèles attendent jusqu'à la toute fin de la journée (Monte Carlo), tandis que d'autres réfléchissent après chaque étape (une étape).
Avant de pouvoir installer sa critique interne, Klukovka doit calculer le nombre de points qu'elle recevra réellement dans chaque état donné.
Mais d'abord!
Voyons comment la cousine de Klukovka, Lis Monte Carlo, calcule la véritable signification de chaque état.
Les modèles de Monte-Carlo ne reflètent pas leur expérience avant la fin du jeu, et comme la valeur du dernier état est nulle, il est très simple de trouver la vraie valeur de cet état précédent comme la somme des récompenses reçues après ce moment.
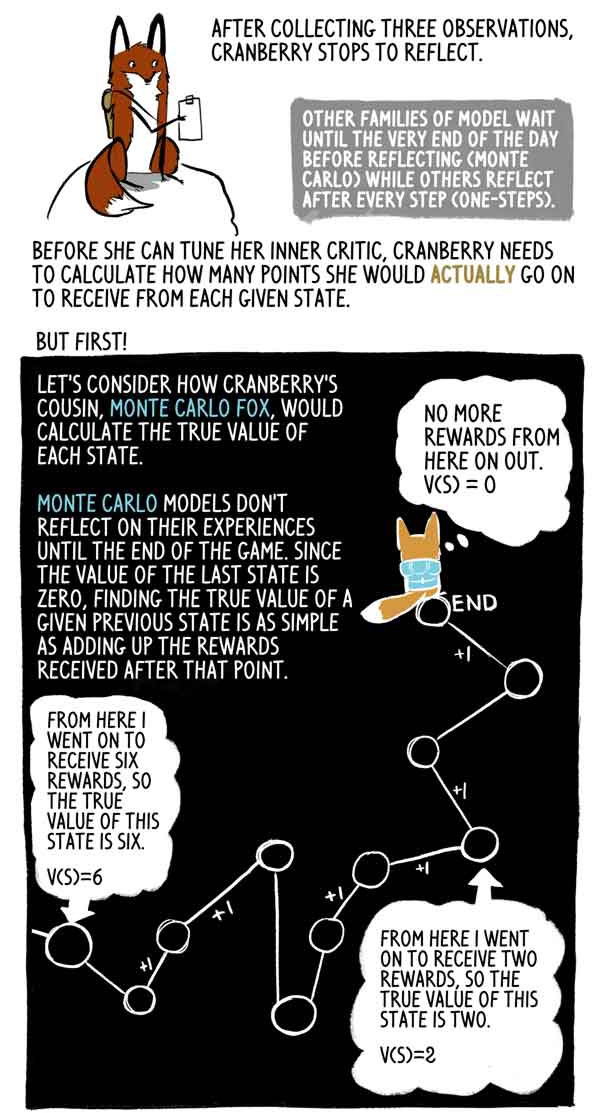
En fait, ce n'est qu'un échantillon à dispersion élevée V (S). L'agent pourrait facilement suivre une trajectoire différente à partir du même état, recevant ainsi une récompense globale différente.
Mais Klyukovka va, s'arrête et réfléchit plusieurs fois jusqu'à la fin de la journée. Elle veut savoir combien de points elle obtiendra réellement de chaque état jusqu'à la fin de la partie, car il reste plusieurs heures avant la fin de la partie.
C'est là qu'elle fait quelque chose de vraiment intelligent - le renard Klyukovka estime combien de points elle recevra pour le dernier état de cet ensemble. Heureusement, elle a une évaluation correcte de son état - son critique.
Avec cette évaluation, Klyukovka peut calculer les valeurs «correctes» des états précédents exactement comme le renard de Monte-Carlo.
Lis Monte Carlo évalue les marques cibles, faisant le déploiement de la trajectoire et ajoutant des récompenses en avant de chaque état. A2C coupe cette trajectoire et la remplace par une évaluation de son critique. Cette charge initiale réduit la variance du score et permet à l'A2C de fonctionner en continu, mais en introduisant un petit biais.

Les récompenses sont souvent réduites pour refléter le fait que la rémunération est maintenant meilleure que dans le futur. Par souci de simplicité, Klukovka ne réduit pas ses récompenses.

Klukovka peut désormais parcourir chaque ligne de données et comparer ses estimations des valeurs d'état à ses valeurs réelles. Elle utilise la différence entre ces chiffres pour perfectionner ses compétences de prédiction. Toutes les trois étapes de la journée, Klyukovka recueille une expérience précieuse qui mérite d'être considérée.
«J'ai mal noté les états 1 et 2. Qu'est-ce que j'ai fait de mal? Ouais! La prochaine fois que je verrai des plumes comme celles-ci, j'augmenterai V (S).
Il peut sembler fou que Klukovka puisse utiliser sa cote V (S) comme base pour la comparer avec d'autres prévisions. Mais les animaux (nous y compris) le font tout le temps! Si vous sentez que les choses vont bien, vous n'avez pas besoin de recycler les actions qui vous ont amené dans cet état.

En ajustant nos sorties calculées et en les remplaçant par une estimation de charge initiale, nous avons remplacé la grande variance de Monte Carlo par un petit biais. Les modèles RL souffrent généralement d'une forte dispersion (représentant tous les chemins possibles), et un tel remplacement en vaut généralement la peine.
Klukovka répète ce processus toute la journée, recueillant trois observations de l'état-action-récompense et y réfléchissant.
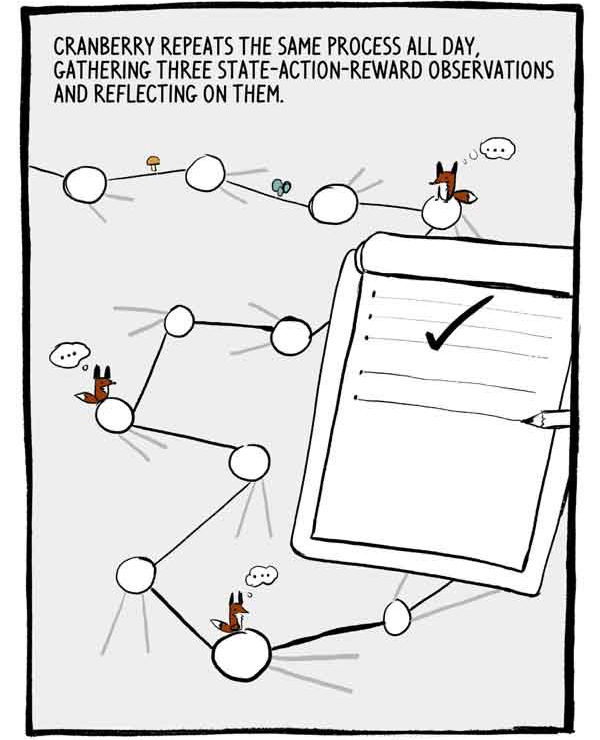
Chaque ensemble de trois observations est une petite série autocorrélée de données d'entraînement étiquetées. Pour réduire cette autocorrélation, de nombreux A2C forment de nombreux agents en parallèle, ajoutant leur expérience ensemble avant de l'envoyer à un réseau neuronal commun.

La journée touche enfin à sa fin. Il ne reste que deux étapes.
Comme nous l'avons dit précédemment, les recommandations des actions de Klukovka sont exprimées en pourcentage de confiance quant à ses capacités. Au lieu de simplement choisir le choix le plus fiable, Klukovka choisit parmi cette distribution d'actions. Cela garantit qu'elle n'accepte pas toujours des actions sûres, mais potentiellement médiocres.
Je pourrais le regretter, mais ... Parfois, en explorant des choses inconnues, vous pouvez venir à de nouvelles découvertes passionnantes ...

Pour encourager davantage la recherche, une valeur appelée entropie est soustraite de la fonction de perte. L'entropie signifie la «portée» de la distribution des actions.
- Il semble que le jeu ait payé!

Ou pas?
Parfois, l'agent est dans un état où toutes les actions conduisent à des résultats négatifs. A2C, cependant, résiste bien aux mauvaises situations.


Lorsque le soleil s'est couché, Klyukovka a réfléchi à la dernière série de solutions.

Nous avons parlé de la façon dont Klyukovka met en place son critique intérieur. Mais comment affine-t-elle son «sujet» intérieur? Comment apprend-elle à faire de tels choix exquis?
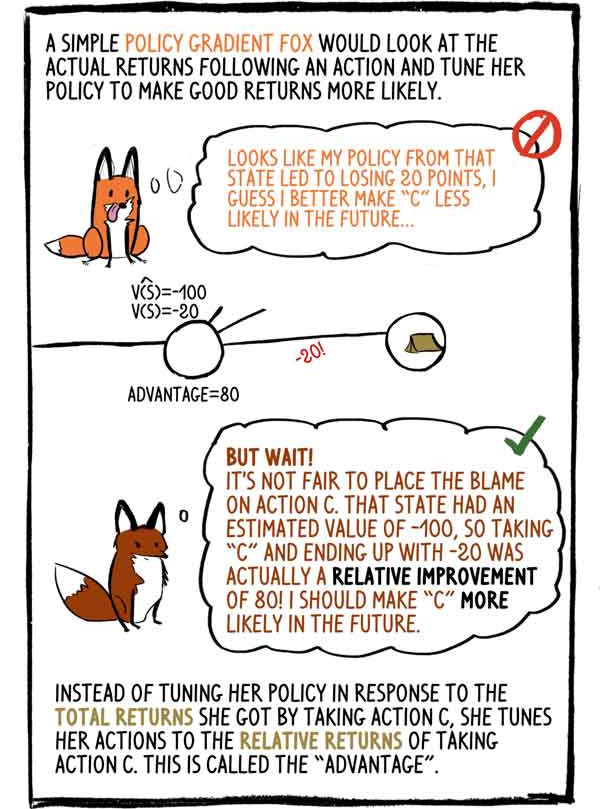
Le renard Gradient-Policy simple d'esprit examinerait le revenu réel après l'action et ajusterait sa politique pour rendre les bons revenus plus probables: - Il semble que ma politique dans cet état a entraîné une perte de 20 points, je pense qu'à l'avenir, il vaut mieux faire "C" moins probable.
- Mais attends! Il est injuste de blâmer l'action «C». Cet état avait une valeur estimée de -100, donc choisir "C" et se terminer par -20 était en fait une amélioration relative de 80! Je dois rendre «C» plus probable à l'avenir.
Au lieu d'ajuster sa politique en fonction des revenus totaux qu'elle a perçus en sélectionnant l'action C, elle ajuste son action aux revenus relatifs de l'action C. C'est ce qu'on appelle un «avantage».
Ce que nous avons appelé un avantage est simplement une erreur. Comme avantage, Klukovka l'utilise pour rendre plus probables des activités étonnamment bonnes. Par erreur, elle utilise le même montant pour pousser sa critique interne à améliorer son évaluation de la valeur du statut.
Le sujet profite de:
- "Wow, ça a mieux fonctionné que je ne le pensais, l'action C doit être une bonne idée."
Le critique utilise l'erreur:
«Mais pourquoi ai-je été surpris? Je n'aurais probablement pas dû évaluer cette condition si négativement. "
Nous pouvons maintenant montrer comment les pertes totales sont calculées - nous minimisons cette fonction pour améliorer notre modèle.
"Perte totale = perte d'action + perte de valeur - entropie"
Veuillez noter que pour calculer les gradients de trois types qualitativement différents, nous prenons les valeurs «à un». Ceci est efficace, mais peut rendre la convergence plus difficile.

Comme tous les animaux, à mesure que Klyukovka vieillit, il affinera sa capacité à prédire les valeurs des états, gagnera plus de confiance dans ses actions et sera moins souvent surpris des récompenses.
Les agents RL, tels que Klukovka, génèrent non seulement toutes les données nécessaires, interagissant simplement avec l'environnement, mais évaluent également les étiquettes cibles elles-mêmes. C'est vrai, les modèles RL mettent à jour les grades précédents pour mieux correspondre aux grades nouveaux et améliorés.
Comme le dit le Dr David Silver, chef du groupe RL chez Google Deepmind: AI = DL + RL. Lorsqu'un agent comme Klyukovka peut définir sa propre intelligence, les possibilités sont infinies ...
