Catalyse des muons en termes de chimie quantique. Partie I: hydrogène ordinaire vs hydrogène muon

Mnogabukaff que la chimie quantique pense au principe de la catalyse muonique: comment exactement le muon abaisse la température du plasma souhaité. En deux parties.

L'essence de la première partie est exprimée en une phrase: le muon est plus lourd que l'électron, il est donc plus difficile de l'arracher du proton.

Mais ceux qui veulent regarder les formules, les graphiques et voir l'essence conceptuelle de la chimie quantique appliquée aux (quasi) atomes les plus simples, sont les bienvenus sous cat.

La deuxième partie est disponible sur ce lien .

Présentation

Ce n'est un secret pour personne que la consommation d'énergie de l'humanité augmente chaque année: chacun de nous a plus de gadgets, il faut se déplacer là-bas, et nous ne sommes pas moins. Par conséquent, Nous sommes constamment en train de penser, où obtenir plus d'énergie et où économiser cette énergie.

La fusion thermonucléaire (TS) est l'une des alternatives possibles aux principales sources d'énergie actuelles (charbon, gaz, centrales hydroélectriques et énergie nucléaire ) . En fait, c'est le bon frère jumeau de l'énergie nucléaire maléfique. La principale chose à ne pas retenir de la bombe tsar est : au lieu des réactions de désintégration nucléaire, la fusion des noyaux légers en noyaux plus lourds sert de source d'énergie. Et tout semble aller pour le mieux: toutes nos sources d'énergie sont apparues d'une manière ou d'une autre grâce au TS, car il circule dans les étoiles (y compris l'intérieur du Soleil) et sert de source de lumière et de chaleur, grâce à laquelle toutes les réactions de photosynthèse se produisent, tout s'écoule les rivières et les vents soufflent. Mais aussi grâce à TS, nous avons un tas d'éléments plus lourds que l'hélium (dont le carbone = charbon, pétrole, gaz et uranium).
Les principales réactions de synthèse putative sont les réactions de fusion de différents isotopes d'hydrogène (protium $$${} _ {1} ^ {1} \ mathrm {H}$ le deutérium $$${} _ {1} ^ {2} \ mathrm {H}$ et tritium $$${} _ {1} ^ {3} \ mathrm {H}$ )

Le problème est que pour démarrer le véhicule en mode autonome, il faut des températures extrêmement élevées. Il n'y a pas de problème avec les étoiles, mais dans des conditions terrestres, une telle exigence est toujours un obstacle au courant provenant d'une fusion thermonucléaire respectueuse de l'environnement dans chaque sortie.

Une façon d'abaisser la température est la catalyse des muons .
Vicki nous dit que le muon ( $$$\ mu ^ -$ ) Est-ce un tel clone d'électrons lourds instable ( $$$e ^ -$ ): il est 207 fois plus lourd qu'un électron et ne vit que 2,2 microsecondes. Mais, il est supposé que l'ajout de telles particules au système où se produit le TS, sera en mesure d'abaisser la température plasmatique minimale nécessaire à la fusion de nouveaux noyaux. Et comme les muons peuvent se former au cours de certaines des réactions de synthèse, au lieu de particules en décomposition, de nouvelles particules devraient apparaître qui continueront de s'engager dans l'alchimie pour brûler l'hydrogène et d'autres éléments avec la formation de plus lourds.

Dans les différences entre les formes habituelles d'hydrogène et celles où l'électron est remplacé par un muon et où réside toute l'essence de la catalyse des muons. Et pour voir cela, nous devons nous tourner vers la chimie quantique et ses concepts, ce que nous ferons.

Dans cette partie, nous nous concentrerons sur les différences dans l'atome d'hydrogène ( $$$\ mathrm {H ^ \ cdot = p ^ + e ^ -}$ ) de son homologue muon ( $$$\ mathrm {p} ^ + \ mu ^ -$ ), dans lequel l'électron est remplacé par un muon.

Survoler le nid du proton ...

Quelques mots courants

Atome d'hydrogène. Tout le monde en discute et se déroule à l'école dans des cours de physique et de chimie, nous allons donc discuter de la manière dont le remplacement d'un électron par un muon affectera ses propriétés (énergie et type d'orbitales).
Nous considérons ces particules à partir de deux positions générales:

• perverti (la soi-disant vieille mécanique quantique),
• et du point de vue de la quantumech normale.

La première considération est à la disposition des écoliers, la seconde nécessitera une connaissance plus approfondie des mathématiques supérieures .

Orbites de Bohr

En fait, l'ancienne mécanique quantique est une tentative d'adapter la mécanique classique pour décrire des systèmes qui ne lui obéissent pas. Malgré le fait que pour une description complète, cette approche soit très imparfaite (dont nous parlerons dans la section suivante), elle est importante et intéressante, et en même temps inhabituellement simple.

• Tout d'abord, c'est grâce à l'ancienne mécanique quantique que les physiciens ont réussi à détecter ce qui n'allait pas avec les systèmes quantiques.Par conséquent, d'un point de vue historique, cette étape était nécessaire et importante pour changer le paradigme de la physique.
• Deuxièmement, la solution de Bohr au problème d'un atome d'atomes de type hydrogène composé de deux particules chargées positivement et négativement pourrait expliquer les observations expérimentales et relier l'ensemble du zoo de séries observé dans les spectres d'hydrogène. Nous examinerons ici une version dommageable de cette décision, qui a amené Bohr le Nobel 1922.

Mais pour résoudre le problème, nous devons nous rappeler comment nous décrivons le mouvement d'une particule dans le cas classique. Il s'agit d'un programme scolaire en physique, mais si quelqu'un a oublié, vous pouvez vous rafraîchir la mémoire ici:




Passons à la tâche. Donc, nous avons deux particules de charges opposées qui sont attirées l'une vers l'autre selon la loi de Coulomb, c'est-à-dire l'énergie potentielle d'attraction est

$$

$$V (R) = \ overbrace {\ frac {1} {4 \ pi \ varepsilon_0}} ^ {k} \ frac {q_1 q_2} {R} = k \ frac {q_1 q_2} {R}$$

où R est la distance entre les particules, $$$q_i$ - charges dans le cas d'un atome d'hydrogène et d'une particule $$$\ mathrm {p} ^ + \ mu ^ -$ ils sont égaux $$$+ e \ environ +1,6 \ fois 10 ^ {- 19}$ CL pour proton et $$$-e$ pour les électrons et les muons, et $\ varepsilon_0$ - constante électrique . Comme les charges sont opposées, l'énergie potentielle diminue avec la distance entre les particules (c'est-à-dire pendant l'approche), ce qui signifie que le proton et l'électron / muon sont attirés l'un vers l'autre.

Cette situation est illustrée dans l'image ci-dessus. Mais quelque part, nous avons vu un système similaire, non? En fait, sur l'une de ces paires que nous vivons: le Soleil + Terre ou Terre + Lune, ou Terre + ISS - ce sont aussi deux particules qui sont attirées par un potentiel similaire exprimé par la loi de Newton:

$$

$$V (R) = -G \ frac {m_1 m_2} {R}$$

où G est la constante gravitationnelle, et $$$m_i$ - masses.

Le proton est 1836 fois plus lourd que l'électron, et comme le muon est 207 fois plus lourd que l'électron, le proton est presque 9 fois plus lourd que le muon. Dans les deux cas, nous avons le système «particules lourdes + particules légères», donc nous prenons l'approximation dans laquelle l'électron / muon tourne autour d'un proton. Bien sûr, la précision de cette hypothèse dans le cas de $$$\ mathrm {p} ^ + \ mu ^ -$ sera significativement plus faible que pour un atome d'hydrogène, mais pour l'illustration, il est tout à fait approprié. Dans le cas du Soleil + Terre, la Terre + ISS utilise généralement des approximations similaires.

Nous sommes intéressés par un système stable dans lequel rien ne tombe nulle part, car les atomes d'hydrogène, s'ils restent intacts, existent depuis très longtemps.

Nous connaissons de tels mouvements dans le cas de tous les analogues du système solaire, et pour la paire Terre + ISS, ils sont même évidents: ce sont des orbites stables auxquelles la station se déplace autour de la Terre à une vitesse suffisante pour ne pas tomber. Cette vitesse est appelée la première vitesse cosmique , c'est-à-dire nous aurions besoin de la première vitesse cosmique pour l'atome d'hydrogène / son homologue muon. Et il est facile de le trouver par les formules scolaires (voir la figure ci-dessus).

Lorsque vous vous déplacez sur une orbite circulaire de rayon R (sur la figure, il est indiqué $$$a_0$ , et bientôt nous y arrivons) vous devez avoir de la vitesse $$$v$ . On peut imaginer qu'à chaque instant deux forces agissant sur une particule volant dans un cercle sont perpendiculaires au vecteur vitesse:

• Coulomb force de gravité dirigée vers le centre qui, selon la définition de la force $$$F = - \ frac {dV} {dR}$ est égal à
  

  $$

  $$F_ \ text {K} = -k \ frac {e ^ 2} {R ^ 2}$$
  
  
• la (fausse) force centrifuge qui essaie d'augmenter le rayon de l'orbite R la contrecarre, son expression a la forme
  

  $$

  $$F_ \ text {q} = \ frac {mv ^ 2} {R}$$
  
  où m est la masse de l'électron / muon (le satellite naturel du proton).
  

La condition pour qu'une particule légère ne s'écrase pas sur une particule lourde est que la somme de ces forces perpendiculaires à la direction du mouvement de la particule soit nulle ( $$$F_ \ mathrm {K} + F_ \ mathrm {q} = 0$ ), ce qui signifie que nous obtenons l'équation

$$

$$\ frac {mv ^ 2} {R} = k \ frac {e ^ 2} {R ^ 2}$$

d'où on obtient la vitesse à laquelle il faut faire voler un électron / muon de masse m au rayon de l'orbite R , pour ne pas s'écraser sur le proton:

$$

$${v} = \ sqrt {k \ frac {e ^ 2} {mR}}$$

Et tout serait blessé si l'électron / muon n'était pas chargé, et les particules chargées émettaient des ondes électromagnétiques lorsqu'elles se déplaçaient dans un cercle (cela s'appelle le frottement rayonnant) , ce qui rendrait un tel système instable: l'électron / muon émettrait de la lumière pendant la rotation, en conséquence, il a perdu de l'énergie et réduit le rayon de son orbite, et finalement il tomberait sur un proton, et il y aurait un petit animal duveteux blanc à tout. Mais, évidemment, cela ne se produit pas, ce qui signifie que quelque chose devrait radicalement différer dans le comportement de particules aussi petites que l'électron / muon.

En fait, Niels Bohr a également proposé une hypothèse très stupide (à l'époque). Il a admis qu'il existe des orbites d'un certain rayon, sur lesquelles l'atome d'hydrogène n'émet rien. Et maintenant, la question est de savoir comment trouver ces orbites. Pour plus de simplicité, nous utiliserons la réalisation plus tard que Bohr: l'expression de la longueur d'onde de Broglie :

$$

$$\ lambda = \ frac {h} {p} = \ frac {h} {mv}$$

On suppose que la matière (particules) a également des propriétés ondulatoires, et on peut leur attribuer une certaine longueur d'onde, qui est donnée par la formule de Broglie. Ensuite, pour que le mouvement dans un cercle soit stationnaire dans le temps (pour être une onde stationnaire), il est nécessaire que la longueur de l'orbite ( $$$L = 2 \ pi R$ ) s'adaptent à un nombre entier d'ondes.

Ensuite, le mouvement ondulatoire de l'électron / muon peut être représenté d'une manière ou d'une autre comme ceci ( tiré du Wiki ):

Dans le langage des formules, cela s'exprime comme suit:

$$

$$2 \ pi R = n \ lambda = n \ frac {h} {mv}$$

En substituant ici la première vitesse cosmique du proton obtenue ci-dessus, nous obtenons l'équation $$$2 \ pi R = \ frac {nh} {m} \ sqrt {\ frac {mR} {ke ^ 2}}$ . Après avoir quadrillé les deux côtés, nous obtenons l'expression du rayon de la nième orbite stationnaire électron / muon:

$$

$$R_n = n ^ 2 \ left (\ overbrace {\ frac {h} {2 \ pi}} ^ {\ hbar} \ right) ^ 2 \ cdot \ frac {1} {mk e ^ 2} = \ frac { n ^ 2 \ hbar ^ 2} {mk e ^ 2}$$

Ici $$$n = 1,2,3, \ ldots$ (nous n'avons pas de limite sur le nombre de vagues à poser), et $$$\ hbar$ - c'est ce qu'on appelle constante de Planck réduite. Plus nous empilons d'ondes, plus le rayon de l'orbite est grand. Avec le rayon minimum ( n = 1) dans le cas d'un électron (c'est-à-dire que m est égal à la masse de l'électron m _e ), ce rayon est appelé rayon de Bohr, comme le dit K.O., en l'honneur de Niels Bohr, et il est noté ₀ (voir Fig. Ci-dessus):

$$

$$a_0 = R_0 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} ke ^ 2}$$

La substitution des nombres ( ħ = 1,054 × 10 ^–34 J · s, m _e = 9,109 × 10 ^-31 kg, k = 8,99 × 10 ⁹ N · m ² · C ⁻² et e = −1,602 × 10 ⁻¹⁹ C) donne la valeur a ₀ = 5,29 × 10 ^-11 m ou 0,529 angströms (Å).


Au cours des calculs, nous avons introduit au passage une nouvelle entité: le nombre $$$n = 1,2,3, \ ldots$ qui détermine le nombre d'ondes et $$$\ Rightarrow$ le rayon de l'orbite, et même la vitesse de l'électron en orbite. Ce nombre est connu de tout le monde depuis l'école: c'est le nombre quantique le plus important d'un atome d'hydrogène. Nous en parlerons plus en détail dans la section suivante, mais pour l'instant vous pouvez essayer de trouver l'énergie de chacun des niveaux.

Comme nous le comprenons, l'énergie d'un système fermé (et il ne fait aucun doute que notre atome d'hydrogène est tel) se compose de deux parties:

• de l'énergie cinétique $$$T = \ frac {mv ^ 2} {2}$ ,
• et le potentiel, qui dans notre cas est donné par la loi de Coulomb $$$V = \ frac {ke ^ 2} {R}$ .

Nous substituons la vitesse et le rayon de l'orbite en eux au nombre principal choisi n . Nous avons déjà écrit le rayon, mais la vitesse ressemblera à $$$v_n ^ 2 = \ frac {k e ^ 2} {m R_n} = \ frac {k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ .

Alors $$$T_n = \ frac {m v_n ^ 2} {2} = \ frac {m} {2} = \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$ . Avec du potentiel, tout est plus simple: $$$V_n = - \ frac {ke ^ 2} {R_n} = - \ frac {m k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ . En résumant ces contributions, nous obtenons l'énergie totale d'un atome d'hydrogène:

$$

$$E_n = T_n + V_n = - \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$$

Et cette formule a grandement contribué à prouver l'exactitude de la mécanique quantique, car des tas de séries de raies spectrales (Lyman, Balmer, Paschen, etc.) ont été observées dans les spectres de l'atome d'hydrogène. Et avec une formule et un modèle simples, ils ont tous réussi à être expliqués à la fois, ce qui était un argument incroyablement convaincant en faveur de la reconnaissance des idées de Bohr.

Après avoir éliminé tous les jus de ce modèle le plus simple, nous pouvons procéder à la bonne considération du problème du point de vue de la mécanique quantique honnête.

Orbitales d'un atome d'hydrogène

La deuxième chose, encore plus importante, est ce qu'est la mécanique quantique et comment elle fonctionne. On peut s'en souvenir de diverses sources. Je recommande:

• pour ne pas aller loin, un article de Habr: Livre «Mécanique quantique. Minimum théorique » (un morceau du livre du même nom de Leonard Sasskind et Art Friedman ),
• livre génial "Comment comprendre la mécanique quantique" du professeur MG MFTIshnogo Ivanova (téléchargeable depuis le lien),
• sur le forum dxdy dans The Chosen, il y a beaucoup de messages qui expliquent bien l'essence du quantumme ,
• revue tout à fait appropriée et article historique sur Lurke ,
• Eh bien, toutes les ordures se trouvent également sur Internet.

  manuel de réseau sur la chimie quantique de VK .
  

Cependant, il y a aussi une compression hardcore des choses nécessaires ici:


Pour trouver comment un électron / muon se déplace dans un champ électrique coulombien créé par un proton, il faut résoudre l'équation de base de la mécanique quantique: l'équation de Schrödinger. Le système considéré étant stationnaire (ne changeant pas dans le temps), il suffit de résoudre sa version simplifiée: l'équation de Schrödinger stationnaire, qui a la forme

$$

$$\ underbrace {(\ overbrace {- \ frac {\ hbar ^ 2} {2m} \ cdot \ left (\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} { \ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2} \ right)} ^ {\ hat {T}} + \ overbrace {- \ frac {ke ^ 2} {R}} ^ {\ hat {V}})} _ {\ hat {H}} \ psi = E \ psi$$

Cette équation est une équation différentielle partielle du second ordre, et nous y recherchons simultanément la fonction d'onde $$$\ psi (x, y, z)$ décrivant l'état spécifique du système et montrant le «maculage» de la particule négative dans l'espace autour du proton, et l'énergie de cet état E. La sorcellerie qui en décide peut se retrouver un peu partout .


Mais une chose plus simple: toute personne familiarisée avec les équations différentielles peut trouver une solution pour l'état fondamental d'un atome d'hydrogène. Afin de ne pas effrayer tout le monde, cette pièce est supprimée dans le spoiler:


Le résultat de la résolution de l'équation de Schrödinger est un ensemble d'orbitales, qui est décrit en utilisant trois entiers n , l et m , appelés «nombres quantiques». La dépendance des énergies de ces orbitales sur $$$(n, l, m)$ donné ci-dessous (et stérilisé à partir d'une ressource fraîche en chimie ):

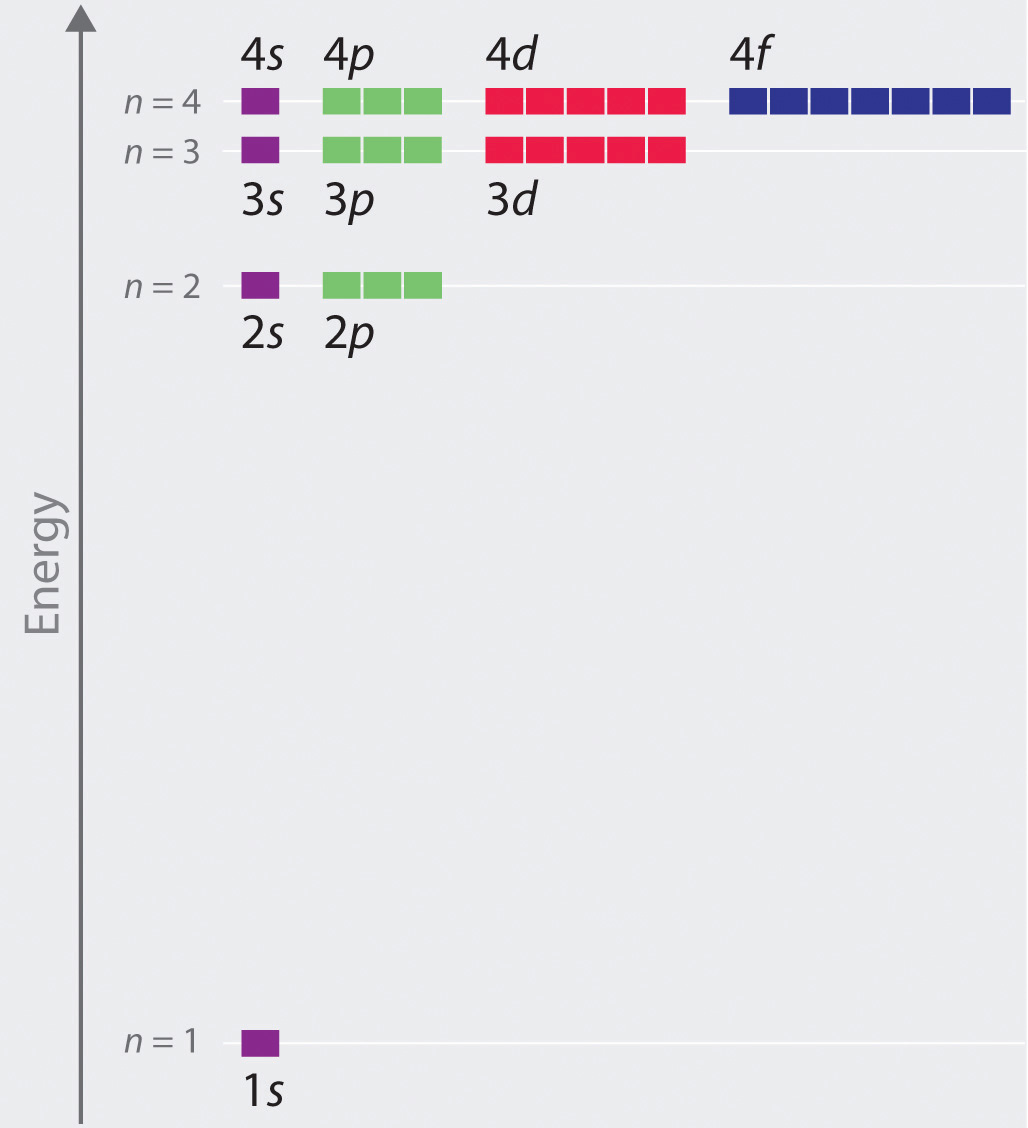
1. Avec le premier nombre, n = 1,2,3, ... nous nous sommes déjà rencontrés. C'est ce qu'on appelle nombre quantique principal. Il détermine l'énergie du niveau, ainsi que la taille de l'orbite de Bohr. (.. ) «». , / , , — , , , . n =1 n =2 ( ):
   
   
   : , n . , .
2. l , , . n , n ( $$$l = 0, 1,2, \ldots, n$ ). , . , , . , ( $$$\psi=0$ ), , . - ( ):
   
   
   
   «» . , .
   
   
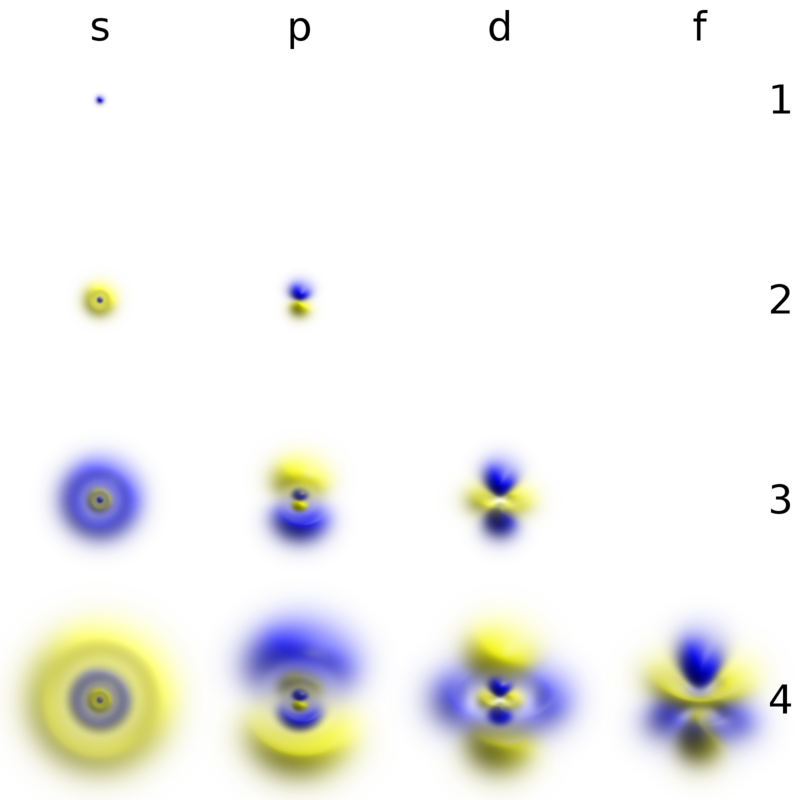
   • $$$l=0$ , , , . s-.
   • ( $$$l=1$ ) p-.
   • 4- $$$l=2$ , d-. .
   • 6- ( $$$l=3$ ) f-.
   • 8- ( $$$l=4$ ) g-.
   • 10- ( $$$l=5$ ) h-.
   • Etc. etc.
   
   , ( n ) , . : , .
   
3. , m , . . 2l+1 : $$$m = -l, -l+1, \ldots, 0 , \ldots , l-1, l$ .

Ce que nous avons obtenu en conséquence: les énergies dans le cas quantique se sont avérées être les mêmes que celles de Bohr, mais le nombre d'états possibles pour un n donné s'est également avéré être un nombre fini. Et ce nombre augmente avec l'augmentation de l'énergie orbitale. De façon inattendue, mais en bon accord avec les expériences.

Alors, quelle est la différence entre un atome d'hydrogène ( $$$\mathrm{H}^\cdot = \mathrm{p^+ e^-}$ ) de son homologue muon ( $$$\mathrm{p}^+ \mu^-$ )?

Nous appliquons maintenant les formules obtenues afin de comprendre ce qui change exactement lorsqu'un électron est remplacé par un muon dans un atome d'hydrogène.

• L'énergie de l'état fondamental (c'est-à-dire le minimum d'énergie, le plus stable, d'où nulle part où aller), avec le nombre quantique principal n = 1. Il est donné par la formule
  

  $$

  $$E_1 = - \frac{m k^2 e^4}{2 \underbrace{n^2}_{1^2} \hbar^2} = - \frac{m k^2 e^4}{2 \hbar^2}$$
  
  Lorsqu'un électron se transfère vers un muon, seule la masse ( $$$m_{\mu} \approx 207 m_\mathrm{e}$ , — , — ). , 207 : $$$E_1(\mathrm{p}^+\mu^-) = 207 E_1(\mathrm{H}^\cdot)$
  
• . //, . $$$\mathrm{A \rightarrow A^+ + e^-}$ , A — . , $$$\mathrm{A \rightarrow A^+ + \mu^-}$ . . $$$E=0$ . $$$E_n = - \frac{m k^2 e^4}{2{n^2}\hbar^2}$ $$$n \rightarrow + \infty$ . C'est-à-dire , , / , , - (. ).
  
  , ( $$$E>0$ , ).
  
  , (IP) +/ :
  

  $$

  $$\mathrm{IP} = \underbrace{0}_{\text{ }} - \underbrace{E_1}_{\text{ }} = -E_1$$
  
  , + 207 , , .. «» , .
  
• , «». , , (1s-)
  

  $$

  $$\psi_{1s}(R) = c\cdot \exp\left(-\frac{R}{R_1} \right)$$
  
  $$$R_1 = \frac{\overbrace{n^2}^{1^2} \hbar^2 }{mk e^2} = \frac{ \hbar^2 }{mk e^2}$ , plus la fonction d'onde diminue avec la distance du proton, et plus sa «taille» est petite, c'est-à-dire localisation d'une particule chargée négativement. Lors du passage d'un électron à un muon, ce rayon R ₁ diminue d'un facteur 207; il s'avère donc que le muon est plus étroitement attaché au proton que l'électron. Et donc, il est plus difficile de l'arracher, car l'ionisation est essentiellement une transition vers une orbite infiniment éloignée, c'est-à-dire le muon doit aller plus que l'électron pour s'échapper du proton.
  

Conceptuellement, toutes nos conclusions des formules sont infiniment simples: résoudre le problème pour $$$\ mathrm {H ^ \ cdot}$ et $$$\ mathrm {p} ^ + \ mu ^ -$ se ressemblent, mais en raison du fait que le muon est plus lourd, il adhère davantage au proton et il lui est plus difficile de s'en échapper.

De toute évidence, non? Mais avec les formules, c'est encore plus évident.

Que se passera-t-il ensuite?

Ce texte n'était qu'une préparation pour la partie suivante.

Dans ce document, nous discuterons directement du mécanisme proposé pour abaisser la température minimale de fusion.

Système atomique PS d'unités

Enfin, nous discutons d'une chose qui nous simplifierait grandement toutes les formules écrites ci-dessus. Dans différentes tâches (même scolaires), le choix des unités de mesure peut grandement faciliter la vie. Et dans le cas de la mécanique quantique, il existe également un système d'unités très pratique. C'est ce qu'on appelle système atomique d'unités . Il appartient à la classe des unités naturelles, qui est essentiellement l'opposé des unités anthropocentriques ( SI , GHS ), dans lesquelles des quantités qu'une personne peut immédiatement imaginer sont utilisées comme pièces de référence. Par exemple, dans SI, l'unité de longueur est un mètre (approximativement la longueur d'un bras / jambe d'un adulte), la masse - un kilogramme (approximativement la masse de bière dans un cercle à l'Oktoberfest), tout cela nous observons dans la vie quotidienne.

Les systèmes naturels d'unités, cependant, prennent comme base quelque chose qui simplifie les formules dans le domaine correspondant de la connaissance. Et dans le cas des unités atomiques:

• tout d'abord, la constante de Planck omniprésente est supposée être l'unité ( $$$\ hbar = 1$ ),
• unité de masse est la masse de l'électron $$$m_ \ mathrm {e} \ environ 9,1 \ fois 10 ^ {- 31}$ kg
• l'unité de charge est la charge de protons (ou, de manière équivalente, le module de charge d'électrons) $$$e = 1,6 \ fois 10 ^ {- 19}$ Kl
• Eh bien, en même temps, la constante électrique est prise comme unité $$$k = \ frac {1} {4 \ pi \ varepsilon_0}$ , à cause de laquelle la loi de Coulomb prend la forme $$$V (R) = \ frac {q_1 q_2} {R}$ .

Dans ce cas, le rayon de Bohr de l'état fondamental de l'atome d'hydrogène devient l'unité de longueur $$$a_0 = R_1 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} k e ^ 2} = 1$ (comme nous nous en souvenons, c'est environ 0,5 Å). L'unité d'énergie devient une valeur appelée Hartree (en l'honneur de l' angle D de Hartree ), qui est notée $$$E_ \ mathrm {h} = \ frac {m_ \ mathrm {e} k ^ 2 e ^ 4} {\ hbar ^ 2} = 1$ . On voit que l'énergie du niveau d'hydrogène 1s en unités atomiques est de 0,5 Hartree.

Dans la prochaine partie, nous siégerons activement dans ces unités.