Comprendre le Q-learning, le problème «Marcher sur un rocher»

Bonjour, Habr! J'attire votre attention sur une traduction de l'article "Comprendre Q-Learning, le problème de la marche en falaise" de Lucas Vazquez .

Dans le dernier article, nous avons présenté le problème «Marcher sur un rocher» et nous sommes installés sur un algorithme terrible qui n'avait pas de sens. Cette fois, nous allons révéler les secrets de cette boîte grise et voir qu'elle n'est pas si effrayante du tout.

Résumé

Nous avons conclu qu'en maximisant le montant des récompenses futures, nous trouvons également le chemin le plus rapide vers l'objectif, donc notre objectif est maintenant de trouver un moyen de le faire!

Introduction à Q-Learning

• Commençons par construire un tableau qui mesure la performance d'une certaine action dans n'importe quel état (nous pouvons la mesurer avec une simple valeur scalaire, donc plus la valeur est grande, meilleure est l'action)
• Ce tableau aura une ligne pour chaque état et une colonne pour chaque action. Dans notre monde, la grille a 48 états (4 par Y par 12 par X) et 4 actions sont autorisées (haut, bas, gauche, droite), donc la table sera de 48 x 4.
• Les valeurs stockées dans ce tableau sont appelées «valeurs Q».
• Ce sont des estimations du montant des récompenses futures. En d'autres termes, ils estiment combien de récompenses supplémentaires nous pouvons obtenir avant la fin du jeu, en étant dans l'état S et en effectuant l'action A.
• Nous initialisons le tableau avec des valeurs aléatoires (ou certaines constantes, par exemple, tous les zéros).

La «table Q» optimale a des valeurs qui nous permettent de prendre les meilleures mesures dans chaque état, nous donnant la meilleure façon de gagner à la fin. Le problème est résolu, cheers, Robot Lords :).

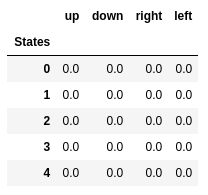Valeurs Q des cinq premiers états.

Q-learning

• Q-learning est un algorithme qui «apprend» ces valeurs.
• À chaque étape, nous obtenons plus d'informations sur le monde.
• Ces informations sont utilisées pour mettre à jour les valeurs du tableau.

Par exemple, supposons que nous soyons à un pas de la cible (carré [2, 11]), et si nous décidons de descendre, nous obtenons une récompense de 0 au lieu de -1.
Nous pouvons utiliser ces informations pour mettre à jour la valeur de la paire état-action dans notre tableau, et la prochaine fois que nous le visiterons, nous saurons déjà que le fait de descendre nous donne une récompense de 0.

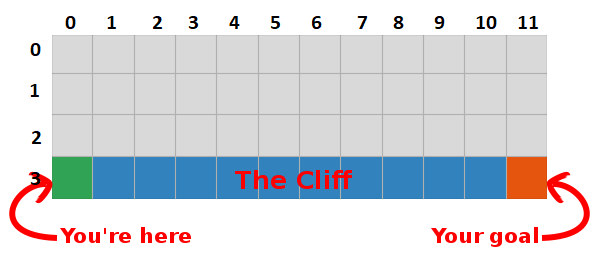
Nous pouvons maintenant diffuser ces informations encore plus loin! Puisque nous connaissons maintenant le chemin vers le but depuis le carré [2, 11], toute action qui nous mène au carré [2, 11] sera également bonne, donc nous mettons à jour la valeur Q du carré, ce qui nous mène à [2, 11] être plus proche de 0.

Et cela, Mesdames et Messieurs, est l'essence même du Q-learning!

Veuillez noter que chaque fois que nous atteignons l'objectif, nous augmentons notre «carte» de la façon d'atteindre l'objectif d'un carré, donc après un nombre suffisant d'itérations, nous aurons une carte complète qui nous montrera comment atteindre l'objectif à partir de chaque état.

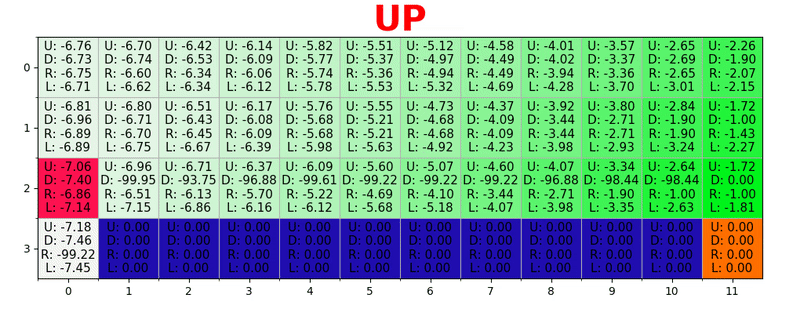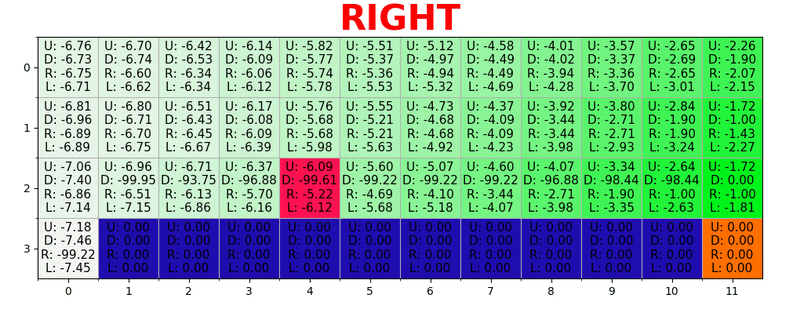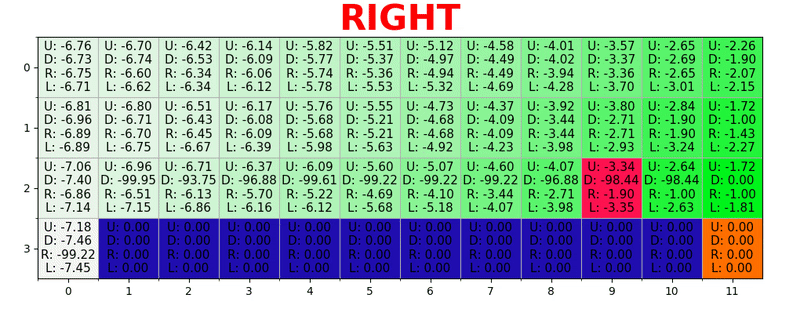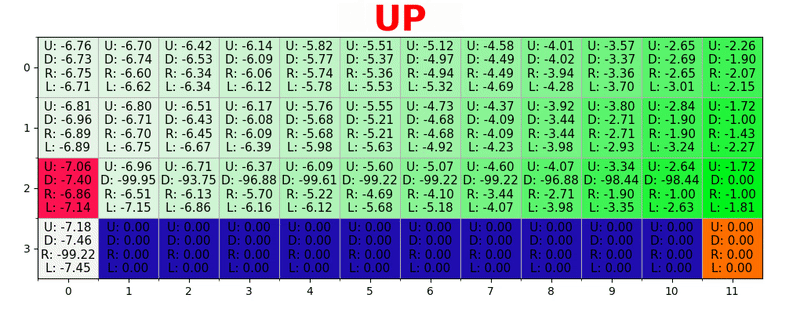Un chemin est généré en prenant la meilleure action dans chaque état. La touche verte représente le sens d'une meilleure action, les touches plus saturées représentent une valeur plus élevée. Le texte représente une valeur pour chaque action (haut, bas, droite, gauche).

Équation de Bellman

Avant de parler de code, parlons des mathématiques: le concept de base du Q-learning, l'équation de Bellman.

• Oublions d'abord γ dans cette équation
• L'équation indique que la valeur Q pour une paire état-action particulière doit être la récompense reçue lors du passage à un nouvel état (en effectuant cette action), ajoutée à la valeur de la meilleure action dans l'état suivant.

En d'autres termes, nous diffusons des informations sur les valeurs des actions une étape à la fois!

Mais nous pouvons décider que recevoir une récompense en ce moment est plus précieux que de recevoir une récompense à l'avenir, et nous avons donc γ, un nombre de 0 à 1 (généralement de 0,9 à 0,99) qui est multiplié par une récompense à l'avenir, réduction des récompenses futures.

Donc, étant donné γ = 0,9 et en appliquant cela à certains états de notre monde (grille), nous avons:

Nous pouvons comparer ces valeurs avec celles ci-dessus dans GIF et voir qu'elles sont identiques.

Implémentation

Maintenant que nous avons une compréhension intuitive du fonctionnement de Q-learning, nous pouvons commencer à réfléchir à la mise en œuvre de tout cela, et nous utiliserons le pseudo-code Q-learning du livre de Sutton comme guide.

Pseudo-code du livre de Sutton.

Code:

# Initialize Q arbitrarily, in this case a table full of zeros q_values = np.zeros((num_states, num_actions)) # Iterate over 500 episodes for _ in range(500): state = env.reset() done = False # While episode is not over while not done: # Choose action action = egreedy_policy(q_values, state, epsilon=0.1) # Do the action next_state, reward, done = env.step(action) # Update q_values td_target = reward + gamma * np.max(q_values[next_state]) td_error = td_target - q_values[state][action] q_values[state][action] += learning_rate * td_error # Update state state = next_state 

• Tout d'abord, nous disons: "Pour tous les états et actions, nous initialisons Q (s, a) arbitrairement", cela signifie que nous pouvons créer notre table de valeurs Q avec toutes les valeurs que nous aimons, elles peuvent être aléatoires, elles peuvent être n'importe quel type de permanent n'a pas d'importance. Nous voyons qu'à la ligne 2, nous créons une table pleine de zéros.

Nous disons également: "La valeur de Q pour les états finaux est nulle", nous ne pouvons entreprendre aucune action dans les états finaux, donc nous considérons que la valeur de toutes les actions dans cet état est nulle.

• Pour chaque épisode, nous devons «initialiser S», c'est juste une façon élégante de dire «redémarrer le jeu», dans notre cas, cela signifie mettre le joueur dans la position de départ; dans notre monde, il existe une méthode qui fait exactement cela, et nous l'appelons à la ligne 6.
• Pour chaque pas de temps (à chaque fois que nous devons agir), nous devons choisir l'action obtenue à partir de Q.

Rappelez-vous, j'ai dit: «prenons-nous les mesures qui ont le plus de valeur dans toutes les conditions?

Lorsque nous faisons cela, nous utilisons nos valeurs Q pour créer la politique; dans ce cas, ce sera une politique gourmande, parce que nous prenons toujours des mesures qui, à notre avis, sont les meilleures dans tous les États, donc on dit que nous agissons avec cupidité.

Indésirable

Mais il y a un problème avec cette approche: imaginez que nous sommes dans un labyrinthe qui a deux récompenses, dont l'une est +1, et l'autre est +100 (et chaque fois que nous en trouvons une, le jeu se termine). Puisque nous prenons toujours des mesures que nous considérons comme les meilleures, nous serons coincés avec le premier prix trouvé, y revenant toujours, donc, si nous reconnaissons d'abord le prix +1, alors nous manquerons le grand prix +100.

Solution

Nous devons nous assurer que nous avons suffisamment étudié notre monde (c'est une tâche incroyablement difficile). C'est là que ε entre en jeu. ε dans l'algorithme gourmand signifie que nous devons agir avec empressement, MAIS faire des actions aléatoires en pourcentage de ε dans le temps, donc avec un nombre infini de tentatives, nous devons examiner tous les états.

L'action est sélectionnée conformément à cette stratégie à la ligne 12, avec epsilon = 0,1, ce qui signifie que nous effectuons des recherches sur le monde 10% du temps. La mise en œuvre de la politique est la suivante:

 def egreedy_policy(q_values, state, epsilon=0.1): # Get a random number from a uniform distribution between 0 and 1, # if the number is lower than epsilon choose a random action if np.random.random() < epsilon: return np.random.choice(4) # Else choose the action with the highest value else: return np.argmax(q_values[state]) 

À la ligne 14 de la première liste, nous appelons la méthode par étapes pour effectuer l'action, le monde nous renvoie le prochain état, la récompense et les informations sur la fin du jeu.

Retour aux maths:

Nous avons une longue équation, réfléchissons-y:

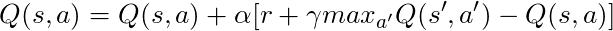
Si nous prenons α = 1:

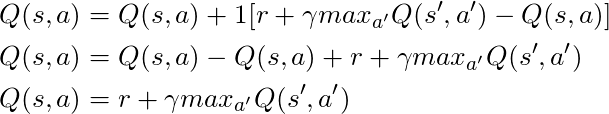
Ce qui correspond exactement à l'équation de Bellman, que nous avons vue il y a quelques paragraphes! Nous savons donc déjà qu'il s'agit de la ligne chargée de diffuser les informations sur les valeurs de l'État.

Mais généralement α (principalement connu sous le nom de vitesse d'apprentissage) est bien inférieur à 1, son objectif principal est d'éviter de grands changements en une seule mise à jour, donc au lieu de voler dans l'objectif, nous l'abordons lentement. Dans notre approche tabulaire, la définition de α = 1 ne pose aucun problème, mais lorsque vous travaillez avec des réseaux de neurones (plus à ce sujet dans les articles suivants), tout peut facilement devenir incontrôlable.

En regardant le code, nous voyons qu'à la ligne 16 de la première liste, nous avons défini td_target, c'est la valeur que nous devrions nous rapprocher, mais au lieu d'aller directement à cette valeur à la ligne 17, nous calculons td_error, nous utiliserons cette valeur en combinaison avec la vitesse apprendre à se déplacer lentement vers l'objectif.

N'oubliez pas que cette équation est une entité Q-Learning.

Maintenant, nous avons juste besoin de mettre à jour notre état, et tout est prêt, c'est la ligne 20. Nous répétons ce processus jusqu'à la fin de l'épisode, en mourant dans les rochers ou en atteignant le but.

Conclusion

Maintenant, nous comprenons et savons intuitivement comment encoder Q-Learning (au moins une version tabulaire), assurez-vous de vérifier tout le code utilisé pour cet article, disponible sur GitHub .

Visualisation du test du processus d'apprentissage:

Veuillez noter que toutes les actions commencent par une valeur supérieure à sa valeur finale, c'est une astuce pour stimuler l'exploration du monde.