Nous avons déjà discuté du moteur d'indexation PostgreSQL et de l' interface des méthodes d'accès , ainsi que de l'index de hachage , l'une des méthodes d'accès. Nous allons maintenant considérer B-tree, l'indice le plus traditionnel et le plus utilisé. Cet article est volumineux, alors soyez patient.

Btree

La structure

Le type d'index B-tree, implémenté comme méthode d'accès "btree", convient aux données qui peuvent être triées. En d'autres termes, les opérateurs "supérieur", "supérieur ou égal", "inférieur", "inférieur ou égal" et "égal" doivent être définis pour le type de données. Notez que les mêmes données peuvent parfois être triées différemment, ce qui nous ramène au concept de famille d'opérateurs.

Comme toujours, les lignes d'index de l'arborescence B sont regroupées dans des pages. Dans les pages feuilles, ces lignes contiennent des données à indexer (clés) et des références aux lignes de table (TID). Dans les pages internes, chaque ligne fait référence à une page enfant de l'index et contient la valeur minimale dans cette page.

Les arbres B ont quelques traits importants:

Les arbres B sont équilibrés, c'est-à-dire que chaque page feuille est séparée de la racine par le même nombre de pages internes. Par conséquent, la recherche d'une valeur prend le même temps.
Les arbres B sont à plusieurs branches, c'est-à-dire que chaque page (généralement 8 Ko) contient un grand nombre de (centaines) TID. En conséquence, la profondeur des arbres B est assez petite, en fait jusqu'à 4 à 5 pour les très grandes tables.
Les données de l'index sont triées dans un ordre non décroissant (à la fois entre les pages et à l'intérieur de chaque page), et les pages de même niveau sont connectées les unes aux autres par une liste bidirectionnelle. Par conséquent, nous pouvons obtenir un ensemble de données ordonné simplement en parcourant une liste dans l'une ou l'autre direction sans retourner à la racine à chaque fois.

Voici un exemple simplifié de l'index sur un champ avec des clés entières.

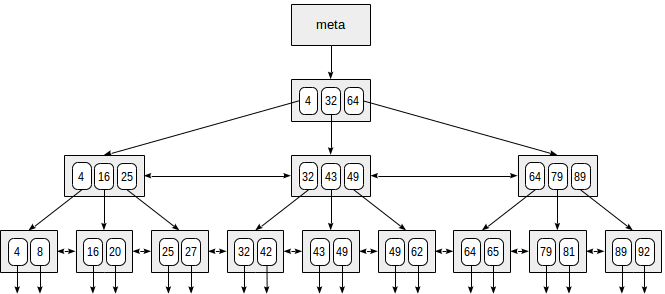
La toute première page de l'index est une métapage, qui fait référence à la racine de l'index. Les nœuds internes sont situés sous la racine et les pages feuilles se trouvent dans la ligne la plus basse. Les flèches vers le bas représentent les références des nœuds feuilles aux lignes de table (TID).

Recherche par égalité

Considérons la recherche d'une valeur dans un arbre par la condition " indexed-field = expression ". Disons, nous sommes intéressés par la clé de 49.

La recherche commence par le nœud racine et nous devons déterminer vers lequel des nœuds enfants descendre. En connaissant les clés du nœud racine (4, 32, 64), nous déterminons donc les plages de valeurs dans les nœuds enfants. Puisque 32 ≤ 49 <64, nous devons descendre jusqu'au deuxième nœud enfant. Ensuite, le même processus est répété récursivement jusqu'à ce que nous atteignions un nœud feuille à partir duquel les TID nécessaires peuvent être obtenus.

En réalité, un certain nombre de détails compliquent ce processus apparemment simple. Par exemple, un index peut contenir des clés non uniques et il peut y avoir tellement de valeurs égales qu'elles ne tiennent pas sur une seule page. Pour revenir à notre exemple, il semble que nous devrions descendre du nœud interne sur la référence à la valeur de 49. Mais, comme le montre clairement la figure, de cette façon, nous allons ignorer l'une des touches "49" dans la page feuille précédente . Par conséquent, une fois que nous avons trouvé une clé exactement égale dans une page interne, nous devons descendre d'une position à gauche, puis parcourir les lignes d'index du niveau sous-jacent de gauche à droite à la recherche de la clé recherchée.

(Une autre complication est que pendant la recherche, d'autres processus peuvent modifier les données: l'arborescence peut être reconstruite, les pages peuvent être divisées en deux, etc. Tous les algorithmes sont conçus pour ces opérations simultanées pour ne pas interférer les uns avec les autres et ne pas provoquer de verrous supplémentaires dans la mesure du possible, mais nous éviterons de développer ce point.)

Recherche par inégalité

Lors de la recherche par la condition " champ indexé ≤ expression " (ou " champ indexé ≥ expression "), nous trouvons d'abord une valeur (le cas échéant) dans l'index par la condition d'égalité " champ indexé = expression ", puis nous parcourons Feuilleter les pages dans le bon sens jusqu'à la fin.

La figure illustre ce processus pour n ≤ 35:

Les opérateurs «supérieur» et «moins» sont pris en charge de la même manière, sauf que la valeur initialement trouvée doit être supprimée.

Recherche par gamme

Lors de la recherche par plage " expression1 ≤ champ indexé ≤ expression2 ", nous trouvons une valeur par condition " champ indexé = expression1 ", puis continuons à parcourir les pages de feuille pendant que la condition " champ indexé ≤ expression2 " est remplie; ou vice versa: commencez par la deuxième expression et marchez dans une direction opposée jusqu'à atteindre la première expression.

La figure montre ce processus pour la condition 23 ≤ n ≤ 64:

Exemple

Voyons un exemple de ce à quoi ressemblent les plans de requête. Comme d'habitude, nous utilisons la base de données de démonstration, et cette fois, nous allons considérer la table des avions. Il ne contient que neuf lignes et le planificateur choisit de ne pas utiliser l'index, car la table entière tient sur une seule page. Mais ce tableau nous intéresse à des fins d'illustration.

demo=# select * from aircrafts;

  aircraft_code | model | range ---------------+---------------------+------- 773 | Boeing 777-300 | 11100 763 | Boeing 767-300 | 7900 SU9 | Sukhoi SuperJet-100 | 3000 320 | Airbus A320-200 | 5700 321 | Airbus A321-200 | 5600 319 | Airbus A319-100 | 6700 733 | Boeing 737-300 | 4200 CN1 | Cessna 208 Caravan | 1200 CR2 | Bombardier CRJ-200 | 2700 (9 rows)

 demo=# create index on aircrafts(range); demo=# set enable_seqscan = off;

(Ou explicitement, "créez un index sur les avions en utilisant btree (range)", mais c'est un arbre B qui est construit par défaut.)

Recherche par égalité:

 demo=# explain(costs off) select * from aircrafts where range = 3000;

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range = 3000) (2 rows)

Recherche par inégalité:

 demo=# explain(costs off) select * from aircrafts where range < 3000;

  QUERY PLAN --------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: (range < 3000) (2 rows)

Et par gamme:

 demo=# explain(costs off) select * from aircrafts where range between 3000 and 5000;

  QUERY PLAN ----------------------------------------------------- Index Scan using aircrafts_range_idx on aircrafts Index Cond: ((range >= 3000) AND (range <= 5000)) (2 rows)

Tri

Soulignons une fois de plus le fait qu'avec tout type d'analyse (index, index uniquement ou bitmap), la méthode d'accès "btree" renvoie les données ordonnées, que nous pouvons clairement voir dans les figures ci-dessus.

Par conséquent, si une table a un index sur la condition de tri, l'optimiseur considérera les deux options: l'analyse d'index de la table, qui retourne facilement les données triées, et l'analyse séquentielle de la table avec tri ultérieur du résultat.

Ordre de tri

Lors de la création d'un index, nous pouvons spécifier explicitement l'ordre de tri. Par exemple, nous pouvons créer un index par plages de vol de cette façon notamment:

 demo=# create index on aircrafts(range desc);

Dans ce cas, des valeurs plus grandes apparaissent dans l'arborescence à gauche, tandis que des valeurs plus petites apparaissent à droite. Pourquoi cela peut-il être nécessaire si nous pouvons parcourir les valeurs indexées dans les deux sens?

Le but est des index multi-colonnes. Créons une vue pour montrer les modèles d'avion avec une division conventionnelle en vaisseaux à courte, moyenne et longue portée:

 demo=# create view aircrafts_v as select model, case when range < 4000 then 1 when range < 10000 then 2 else 3 end as class from aircrafts; demo=# select * from aircrafts_v;

  model | class ---------------------+------- Boeing 777-300 | 3 Boeing 767-300 | 2 Sukhoi SuperJet-100 | 1 Airbus A320-200 | 2 Airbus A321-200 | 2 Airbus A319-100 | 2 Boeing 737-300 | 2 Cessna 208 Caravan | 1 Bombardier CRJ-200 | 1 (9 rows)

Et créons un index (en utilisant l'expression):

 demo=# create index on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end), model);

Maintenant, nous pouvons utiliser cet index pour obtenir des données triées par les deux colonnes dans l'ordre croissant:

 demo=# select class, model from aircrafts_v order by class, model;

  class | model -------+--------------------- 1 | Bombardier CRJ-200 1 | Cessna 208 Caravan 1 | Sukhoi SuperJet-100 2 | Airbus A319-100 2 | Airbus A320-200 2 | Airbus A321-200 2 | Boeing 737-300 2 | Boeing 767-300 3 | Boeing 777-300 (9 rows)

 demo=# explain(costs off) select class, model from aircrafts_v order by class, model;

  QUERY PLAN -------------------------------------------------------- Index Scan using aircrafts_case_model_idx on aircrafts (1 row)

De même, nous pouvons effectuer la requête pour trier les données dans l'ordre décroissant:

 demo=# select class, model from aircrafts_v order by class desc, model desc;

  class | model -------+--------------------- 3 | Boeing 777-300 2 | Boeing 767-300 2 | Boeing 737-300 2 | Airbus A321-200 2 | Airbus A320-200 2 | Airbus A319-100 1 | Sukhoi SuperJet-100 1 | Cessna 208 Caravan 1 | Bombardier CRJ-200 (9 rows)

 demo=# explain(costs off) select class, model from aircrafts_v order by class desc, model desc;

  QUERY PLAN ----------------------------------------------------------------- Index Scan BACKWARD using aircrafts_case_model_idx on aircrafts (1 row)

Cependant, nous ne pouvons pas utiliser cet index pour obtenir des données triées par une colonne en ordre décroissant et par l'autre colonne en ordre croissant. Cela nécessitera un tri séparé:

 demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC;

  QUERY PLAN ------------------------------------------------- Sort Sort Key: (CASE ... END), aircrafts.model DESC -> Seq Scan on aircrafts (3 rows)

(Notez qu'en dernier recours, le planificateur a choisi le balayage séquentiel indépendamment du paramètre "enable_seqscan = off" effectué précédemment. En effet, ce paramètre n'interdit pas le balayage de la table, mais définit uniquement son coût astronomique - veuillez consulter le plan avec "Coûts sur".)

Pour que cette requête utilise l'index, ce dernier doit être construit avec le sens de tri requis:

 demo=# create index aircrafts_case_asc_model_desc_idx on aircrafts( (case when range < 4000 then 1 when range < 10000 then 2 else 3 end) ASC, model DESC); demo=# explain(costs off) select class, model from aircrafts_v order by class ASC, model DESC;

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_case_asc_model_desc_idx on aircrafts (1 row)

Ordre des colonnes

Un autre problème qui se pose lors de l'utilisation d'index multi-colonnes est l'ordre de listage des colonnes dans un index. Pour B-tree, cet ordre est d'une importance capitale: les données à l'intérieur des pages seront triées par le premier champ, puis par le second, et ainsi de suite.

Nous pouvons représenter l'indice que nous avons construit sur des intervalles de plage et des modèles de manière symbolique comme suit:

En fait, un si petit index conviendra à coup sûr à une page racine. Dans la figure, il est délibérément distribué sur plusieurs pages pour plus de clarté.

Il ressort clairement de ce tableau que la recherche par des prédicats tels que "classe = 3" (recherche uniquement par le premier champ) ou "classe = 3 et modèle = 'Boeing 777-300'" "(recherche par les deux champs) fonctionnera efficacement.

Cependant, la recherche par le prédicat «model = 'Boeing 777-300'» sera beaucoup moins efficace: à partir de la racine, nous ne pouvons pas déterminer vers quel nœud enfant descendre, par conséquent, nous devrons descendre vers chacun d'eux. Cela ne signifie pas qu'un indice comme celui-ci ne peut jamais être utilisé - son efficacité est en cause. Par exemple, si nous avions trois classes d'avions et un grand nombre de modèles dans chaque classe, nous aurions à parcourir environ un tiers de l'indice et cela aurait pu être plus efficace que le balayage complet de la table ... ou pas.

Cependant, si nous créons un index comme celui-ci:

 demo=# create index on aircrafts( model, (case when range < 4000 then 1 when range < 10000 then 2 else 3 end));

l'ordre des champs va changer:

Avec cet index, la recherche par le prédicat "model = 'Boeing 777-300'" fonctionnera efficacement, mais la recherche par le prédicat "class = 3" ne fonctionnera pas.

Nulls

La méthode d'accès "Btree" indexe les valeurs NULL et prend en charge la recherche par conditions IS NULL et IS NOT NULL.

Prenons le tableau des vols, où les NULL se produisent:

 demo=# create index on flights(actual_arrival); demo=# explain(costs off) select * from flights where actual_arrival is null;

  QUERY PLAN ------------------------------------------------------- Bitmap Heap Scan on flights Recheck Cond: (actual_arrival IS NULL) -> Bitmap Index Scan on flights_actual_arrival_idx Index Cond: (actual_arrival IS NULL) (4 rows)

Les valeurs NULL sont situées à l'une ou à l'autre extrémité des nœuds terminaux selon la façon dont l'index a été créé (NULLS FIRST ou NULLS LAST). Ceci est important si une requête inclut le tri: l'index peut être utilisé si la commande SELECT spécifie le même ordre de NULL dans sa clause ORDER BY que l'ordre spécifié pour l'index construit (NULLS FIRST ou NULLS LAST).

Dans l'exemple suivant, ces ordres sont les mêmes, par conséquent, nous pouvons utiliser l'index:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS LAST;

  QUERY PLAN -------------------------------------------------------- Index Scan using flights_actual_arrival_idx on flights (1 row)

Et ici, ces ordres sont différents, et l'optimiseur choisit un balayage séquentiel avec un tri ultérieur:

 demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST;

  QUERY PLAN ---------------------------------------- Sort Sort Key: actual_arrival NULLS FIRST -> Seq Scan on flights (3 rows)

Pour utiliser l'index, il doit être créé avec des valeurs NULL situées au début:

 demo=# create index flights_nulls_first_idx on flights(actual_arrival NULLS FIRST); demo=# explain(costs off) select * from flights order by actual_arrival NULLS FIRST;

  QUERY PLAN ----------------------------------------------------- Index Scan using flights_nulls_first_idx on flights (1 row)

Des problèmes comme celui-ci sont certainement dus au fait que les valeurs NULL ne sont pas triables, c'est-à-dire que le résultat de la comparaison pour NULL et toute autre valeur n'est pas défini:

 demo=# \pset null NULL demo=# select null < 42;

  ?column? ---------- NULL (1 row)

Cela va à l'encontre du concept d'arbre B et ne correspond pas au schéma général. Les NULL, cependant, jouent un rôle si important dans les bases de données que nous devons toujours leur faire des exceptions.

Étant donné que les valeurs NULL peuvent être indexées, il est possible d'utiliser un index même sans aucune condition imposée à la table (car l'index contient des informations sur toutes les lignes de la table à coup sûr). Cela peut avoir du sens si la requête nécessite un classement des données et que l'index garantit l'ordre requis. Dans ce cas, le planificateur peut plutôt choisir l'accès à l'index pour économiser sur un tri séparé.

Propriétés

Examinons les propriétés de la méthode d'accès "btree" (des requêtes ont déjà été fournies ).

  amname | name | pg_indexam_has_property --------+---------------+------------------------- btree | can_order | t btree | can_unique | t btree | can_multi_col | t btree | can_exclude | t

Comme nous l'avons vu, B-tree peut ordonner les données et prend en charge l'unicité - et c'est la seule méthode d'accès à nous fournir des propriétés comme celles-ci. Les index multicolonnes sont également autorisés, mais d'autres méthodes d'accès (mais pas toutes) peuvent également prendre en charge de tels index. Nous discuterons de la prise en charge de la contrainte EXCLUDE la prochaine fois, et non sans raison.

  name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | t

La méthode d'accès "Btree" prend en charge les deux techniques pour obtenir des valeurs: l'analyse d'index, ainsi que l'analyse bitmap. Et comme nous avons pu le voir, la méthode d'accès peut parcourir l'arborescence à la fois "en avant" et "en arrière".

  name | pg_index_column_has_property --------------------+------------------------------ asc | t desc | f nulls_first | f nulls_last | t orderable | t distance_orderable | f returnable | t search_array | t search_nulls | t

Les quatre premières propriétés de cette couche expliquent comment les valeurs exactes d'une certaine colonne spécifique sont ordonnées. Dans cet exemple, les valeurs sont triées dans l'ordre croissant ("asc") et les valeurs NULL sont fournies en dernier ("nulls_last"). Mais comme nous l'avons déjà vu, d'autres combinaisons sont possibles.

La propriété "Search_array" indique la prise en charge d'expressions comme celle-ci par l'index:

 demo=# explain(costs off) select * from aircrafts where aircraft_code in ('733','763','773');

  QUERY PLAN ----------------------------------------------------------------- Index Scan using aircrafts_pkey on aircrafts Index Cond: (aircraft_code = ANY ('{733,763,773}'::bpchar[])) (2 rows)

La propriété "renvoyable" indique la prise en charge de l'analyse d'index uniquement, ce qui est raisonnable car les lignes de l'index stockent elles-mêmes les valeurs indexées (contrairement à l'index de hachage, par exemple). Ici, il est logique de dire quelques mots sur la couverture des index basés sur l'arbre B.

Index uniques avec lignes supplémentaires

Comme nous l'avons vu précédemment , un index de couverture est celui qui stocke toutes les valeurs nécessaires pour une requête, l'accès à la table elle-même n'étant pas (presque) requis. Un index unique peut spécifiquement couvrir.

Mais supposons que nous voulons ajouter les colonnes supplémentaires nécessaires pour une requête à l'index unique. Cependant, l'unicité de ces valeurs composites ne garantit pas l'unicité de la clé, et deux index sur les mêmes colonnes seront alors nécessaires: un unique pour prendre en charge la contrainte d'intégrité et un autre pour être utilisé comme couverture. C'est inefficace à coup sûr.

Dans notre entreprise, Anastasiya Lubennikova lubennikovaav a amélioré la méthode "btree" afin que des colonnes supplémentaires, non uniques, puissent être incluses dans un index unique. Nous espérons que ce correctif sera adopté par la communauté pour faire partie de PostgreSQL, mais cela ne se produira pas dès la version 10. À ce stade, le correctif est disponible dans Pro Standard 9.5+, et voici à quoi il ressemble comme.

En fait, ce correctif a été validé pour PostgreSQL 11.

Prenons le tableau des réservations:

 demo=# \d bookings

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey" PRIMARY KEY, btree (book_ref) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)

Dans ce tableau, la clé primaire (book_ref, code de réservation) est fournie par un index "btree" régulier. Créons un nouvel index unique avec une colonne supplémentaire:

 demo=# create unique index bookings_pkey2 on bookings(book_ref) INCLUDE (book_date);

Maintenant, nous remplaçons l'index existant par un nouveau (dans la transaction, pour appliquer toutes les modifications simultanément):

 demo=# begin; demo=# alter table bookings drop constraint bookings_pkey cascade; demo=# alter table bookings add primary key using index bookings_pkey2; demo=# alter table tickets add foreign key (book_ref) references bookings (book_ref); demo=# commit;

Voici ce que nous obtenons:

 demo=# \d bookings

  Table "bookings.bookings" Column | Type | Modifiers --------------+--------------------------+----------- book_ref | character(6) | not null book_date | timestamp with time zone | not null total_amount | numeric(10,2) | not null Indexes: "bookings_pkey2" PRIMARY KEY, btree (book_ref) INCLUDE (book_date) Referenced by: TABLE "tickets" CONSTRAINT "tickets_book_ref_fkey" FOREIGN KEY (book_ref) REFERENCES bookings(book_ref)

Désormais, un seul et même index fonctionne comme unique et sert d'index de couverture pour cette requête, par exemple:

 demo=# explain(costs off) select book_ref, book_date from bookings where book_ref = '059FC4';

  QUERY PLAN -------------------------------------------------- Index Only Scan using bookings_pkey2 on bookings Index Cond: (book_ref = '059FC4'::bpchar) (2 rows)

Création de l'index

Il est bien connu, mais non moins important, que pour une table de grande taille, il est préférable d'y charger des données sans index et de créer les index nécessaires ultérieurement. Ce n'est pas seulement plus rapide, mais très probablement l'indice aura une taille plus petite.

Le fait est que la création de l'index "btree" utilise un processus plus efficace que l'insertion de valeurs par ligne dans l'arbre. En gros, toutes les données disponibles dans le tableau sont triées et des pages feuilles de ces données sont créées. Ensuite, les pages internes sont "construites" sur cette base jusqu'à ce que toute la pyramide converge vers la racine.

La vitesse de ce processus dépend de la taille de la RAM disponible, qui est limitée par le paramètre "maintenance_work_mem". Ainsi, l'augmentation de la valeur du paramètre peut accélérer le processus. Pour les index uniques, une mémoire de taille "work_mem" est allouée en plus de "maintenance_work_mem".

Sémantique de comparaison

La dernière fois, nous avons mentionné que PostgreSQL a besoin de savoir quelles fonctions de hachage appeler des valeurs de différents types et que cette association est stockée dans la méthode d'accès "hachage". De même, le système doit comprendre comment ordonner les valeurs. Cela est nécessaire pour les tri, les regroupements (parfois), les jointures de fusion, etc. PostgreSQL ne se lie pas aux noms d'opérateurs (tels que>, <, =) car les utilisateurs peuvent définir leur propre type de données et donner aux opérateurs correspondants des noms différents. Une famille d'opérateurs utilisée par la méthode d'accès "btree" définit à la place des noms d'opérateurs.

Par exemple, ces opérateurs de comparaison sont utilisés dans la famille d'opérateurs "bool_ops":

 postgres=# select amop.amopopr::regoperator as opfamily_operator, amop.amopstrategy from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'bool_ops' order by amopstrategy;

  opfamily_operator | amopstrategy ---------------------+-------------- <(boolean,boolean) | 1 <=(boolean,boolean) | 2 =(boolean,boolean) | 3 >=(boolean,boolean) | 4 >(boolean,boolean) | 5 (5 rows)

Ici, nous pouvons voir cinq opérateurs de comparaison, mais comme déjà mentionné, nous ne devons pas nous fier à leurs noms. Pour comprendre quelle comparaison chaque opérateur fait, le concept de stratégie est introduit. Cinq stratégies sont définies pour décrire la sémantique des opérateurs:

1 - moins
2 - inférieur ou égal
3 - égal
4 - supérieur ou égal
5 - plus

Certaines familles d'opérateurs peuvent contenir plusieurs opérateurs mettant en œuvre une stratégie. Par exemple, la famille d'opérateurs "integer_ops" contient les opérateurs suivants pour la stratégie 1:

 postgres=# select amop.amopopr::regoperator as opfamily_operator from pg_am am, pg_opfamily opf, pg_amop amop where opf.opfmethod = am.oid and amop.amopfamily = opf.oid and am.amname = 'btree' and opf.opfname = 'integer_ops' and amop.amopstrategy = 1 order by opfamily_operator;

  opfamily_operator ---------------------- <(integer,bigint) <(smallint,smallint) <(integer,integer) <(bigint,bigint) <(bigint,integer) <(smallint,integer) <(integer,smallint) <(smallint,bigint) <(bigint,smallint) (9 rows)

Grâce à cela, l'optimiseur peut éviter les conversions de types lors de la comparaison des valeurs de différents types contenus dans une famille d'opérateurs.

Prise en charge de l'index pour un nouveau type de données

La documentation fournit un exemple de création d'un nouveau type de données pour les nombres complexes et d'une classe d'opérateur pour trier les valeurs de ce type. Cet exemple utilise le langage C, ce qui est absolument raisonnable lorsque la vitesse est critique. Mais rien ne nous empêche d'utiliser du SQL pur pour la même expérience afin d'essayer de mieux comprendre la sémantique de comparaison.

Créons un nouveau type composite avec deux champs: les parties réelles et imaginaires.

 postgres=# create type complex as (re float, im float);

Nous pouvons créer une table avec un champ du nouveau type et ajouter quelques valeurs à la table:

 postgres=# create table numbers(x complex); postgres=# insert into numbers values ((0.0, 10.0)), ((1.0, 3.0)), ((1.0, 1.0));

Maintenant une question se pose: comment ordonner des nombres complexes si aucune relation d'ordre n'est définie pour eux au sens mathématique?

Il s'avère que les opérateurs de comparaison sont déjà définis pour nous:

 postgres=# select * from numbers order by x;

  x -------- (0,10) (1,1) (1,3) (3 rows)

Par défaut, le tri s'effectue par composant pour un type composite: les premiers champs sont comparés, puis les deuxièmes, etc., à peu près de la même manière que les chaînes de texte sont comparées caractère par caractère. Mais nous pouvons définir un ordre différent. Par exemple, les nombres complexes peuvent être traités comme des vecteurs et ordonnés par le module (longueur), qui est calculé comme la racine carrée de la somme des carrés des coordonnées (le théorème de Pythagore). Pour définir un tel ordre, créons une fonction auxiliaire qui calcule le module:

 postgres=# create function modulus(a complex) returns float as $$ select sqrt(a.re*a.re + a.im*a.im); $$ immutable language sql;

Nous allons maintenant définir systématiquement des fonctions pour les cinq opérateurs de comparaison en utilisant cette fonction auxiliaire:

 postgres=# create function complex_lt(a complex, b complex) returns boolean as $$ select modulus(a) < modulus(b); $$ immutable language sql; postgres=# create function complex_le(a complex, b complex) returns boolean as $$ select modulus(a) <= modulus(b); $$ immutable language sql; postgres=# create function complex_eq(a complex, b complex) returns boolean as $$ select modulus(a) = modulus(b); $$ immutable language sql; postgres=# create function complex_ge(a complex, b complex) returns boolean as $$ select modulus(a) >= modulus(b); $$ immutable language sql; postgres=# create function complex_gt(a complex, b complex) returns boolean as $$ select modulus(a) > modulus(b); $$ immutable language sql;

Et nous allons créer des opérateurs correspondants. Pour illustrer qu'ils n'ont pas besoin d'être appelés ">", "<", etc., donnons-leur des noms "bizarres".

 postgres=# create operator #<#(leftarg=complex, rightarg=complex, procedure=complex_lt); postgres=# create operator #<=#(leftarg=complex, rightarg=complex, procedure=complex_le); postgres=# create operator #=#(leftarg=complex, rightarg=complex, procedure=complex_eq); postgres=# create operator #>=#(leftarg=complex, rightarg=complex, procedure=complex_ge); postgres=# create operator #>#(leftarg=complex, rightarg=complex, procedure=complex_gt);

À ce stade, nous pouvons comparer les chiffres:

 postgres=# select (1.0,1.0)::complex #<# (1.0,3.0)::complex;

  ?column? ---------- t (1 row)

En plus de cinq opérateurs, la méthode d'accès «btree» nécessite de définir une fonction (excessive mais pratique): elle doit retourner -1, 0 ou 1 si la première valeur est inférieure, égale ou supérieure à la seconde un. Cette fonction auxiliaire est appelée support. D'autres méthodes d'accès peuvent nécessiter la définition d'autres fonctions de support.

 postgres=# create function complex_cmp(a complex, b complex) returns integer as $$ select case when modulus(a) < modulus(b) then -1 when modulus(a) > modulus(b) then 1 else 0 end; $$ language sql;

Nous sommes maintenant prêts à créer une classe d'opérateurs (et la famille d'opérateurs du même nom sera créée automatiquement):

 postgres=# create operator class complex_ops default for type complex using btree as operator 1 #<#, operator 2 #<=#, operator 3 #=#, operator 4 #>=#, operator 5 #>#, function 1 complex_cmp(complex,complex);

Maintenant, le tri fonctionne comme vous le souhaitez:

 postgres=# select * from numbers order by x;

  x -------- (1,1) (1,3) (0,10) (3 rows)

Et il sera certainement soutenu par l'index "btree".

Pour compléter l'image, vous pouvez obtenir des fonctions de support en utilisant cette requête:

 postgres=# select amp.amprocnum, amp.amproc, amp.amproclefttype::regtype, amp.amprocrighttype::regtype from pg_opfamily opf, pg_am am, pg_amproc amp where opf.opfname = 'complex_ops' and opf.opfmethod = am.oid and am.amname = 'btree' and amp.amprocfamily = opf.oid;

  amprocnum | amproc | amproclefttype | amprocrighttype -----------+-------------+----------------+----------------- 1 | complex_cmp | complex | complex (1 row)

Internes

Nous pouvons explorer la structure interne de B-tree en utilisant l'extension "pageinspect".

 demo=# create extension pageinspect;

Métapage d'index:

 demo=# select * from bt_metap('ticket_flights_pkey');

  magic | version | root | level | fastroot | fastlevel --------+---------+------+-------+----------+----------- 340322 | 2 | 164 | 2 | 164 | 2 (1 row)

Le plus intéressant ici est le niveau d'index: l'index sur deux colonnes pour une table avec un million de lignes requis aussi peu que 2 niveaux (hors racine).

Informations statistiques sur le bloc 164 (racine):

 demo=# select type, live_items, dead_items, avg_item_size, page_size, free_size from bt_page_stats('ticket_flights_pkey',164);

  type | live_items | dead_items | avg_item_size | page_size | free_size ------+------------+------------+---------------+-----------+----------- r | 33 | 0 | 31 | 8192 | 6984 (1 row)

Et les données du bloc (le champ "data", qui est ici sacrifié à la largeur de l'écran, contient la valeur de la clé d'indexation en représentation binaire):

 demo=# select itemoffset, ctid, itemlen, left(data,56) as data from bt_page_items('ticket_flights_pkey',164) limit 5;

  itemoffset | ctid | itemlen | data ------------+---------+---------+---------------------------------------------------------- 1 | (3,1) | 8 | 2 | (163,1) | 32 | 1d 30 30 30 35 34 33 32 33 30 35 37 37 31 00 00 ff 5f 00 3 | (323,1) | 32 | 1d 30 30 30 35 34 33 32 34 32 33 36 36 32 00 00 4f 78 00 4 | (482,1) | 32 | 1d 30 30 30 35 34 33 32 35 33 30 38 39 33 00 00 4d 1e 00 5 | (641,1) | 32 | 1d 30 30 30 35 34 33 32 36 35 35 37 38 35 00 00 2b 09 00 (5 rows)

Le premier élément concerne les techniques et spécifie la limite supérieure de tous les éléments du bloc (un détail d'implémentation dont nous n'avons pas discuté), tandis que les données elles-mêmes commencent par le deuxième élément. Il est clair que le nœud enfant le plus à gauche est le bloc 163, suivi du bloc 323, et ainsi de suite. Ils peuvent à leur tour être explorés en utilisant les mêmes fonctions.

Maintenant, suivant une bonne tradition, il est logique de lire la documentation, le fichier README et le code source.

Pourtant, une autre extension potentiellement utile est " amcheck ", qui sera incorporée dans PostgreSQL 10, et pour les versions inférieures, vous pouvez l'obtenir depuis github . Cette extension vérifie la cohérence logique des données dans les arbres B et nous permet de détecter à l'avance les défauts.

C'est vrai, "amcheck" fait partie de PostgreSQL à partir de la version 10.

Continuez à lire .

Index dans PostgreSQL - 4 (Btree)