Enfin, un guide en russe de la langue Julia est apparu. Il fournit une introduction complète au langage pour ceux qui ont peu d'expérience en programmation (le reste sera utile pour le développement général), il y a aussi une introduction à l'apprentissage automatique et un tas de tâches pour consolider le matériel.
Pendant la recherche, je suis tombé sur un cours de programmation pour les économistes (en plus de Julia, il y a aussi Python). Les expérimentés peuvent suivre un cours rapide ou lire le livre Comment penser comme un informaticien
Ce qui suit est une traduction de matériel du blog de Christopher Rackauckas 7 Julia Gotchas et Comment les manipuler
Permettez-moi de commencer par dire que Julia est une langue merveilleuse. Je l'aime, c'est ce que je considère comme le langage le plus puissant et intuitif que j'aie jamais utilisé. C'est sans aucun doute ma langue préférée. Cependant, il y a des «pièges», des petites choses délicates que vous devez savoir. Chaque langue en a, et l'une des premières choses que vous devez faire pour maîtriser la langue est de découvrir ce qu'elles sont et comment les éviter. Le but de cet article est de vous aider à accélérer ce processus en exposant certaines des
Julia est un bon langage pour comprendre ce qui se passe, car il n'y a pas de magie en elle. Les développeurs de Julia souhaitaient avoir des règles de conduite clairement définies. Cela signifie que tout comportement peut être expliqué. Cependant, cela peut signifier que vous devez vous forcer la tête pour comprendre pourquoi cela et non l'autre se produit. C'est pourquoi je ne vais pas seulement décrire quelques problèmes communs, mais je vais aussi expliquer pourquoi ils se posent. Vous verrez qu'il existe des schémas très similaires, et une fois que vous en aurez pris conscience, vous ne vous moquerez plus d'aucun d'entre eux. Pour cette raison, Julia a une courbe d'apprentissage légèrement plus abrupte par rapport aux langages plus simples comme MATLAB / R / Python . Cependant, une fois que vous aurez maîtrisé cela, vous pourrez utiliser pleinement le laconicisme de Julia pour obtenir des performances C / Fortran . Maintenant, creusez plus profondément.
De façon inattendue: REPL (terminal) a une portée globale
C'est de loin le problème le plus courant signalé par les nouveaux utilisateurs de Julia. Quelqu'un dira: «J'ai entendu, Julia est rapide!», Ouvrez REPL, écrivez rapidement un algorithme bien connu et exécutez ce script. Après son exécution, ils regardent le temps et disent: "Attendez une seconde, pourquoi est-ce lent, comme en Python?" Étant donné qu'il s'agit d'un problème si important et courant, passons un peu de temps à explorer les raisons pour lesquelles cela se produit afin de savoir comment éviter cela.
Une petite digression: pourquoi Julia est rapide
Vous devez comprendre que Julia n'est pas seulement une compilation de code, mais aussi une spécialisation de types (c'est-à-dire une compilation de code spécifique à ces types). Permettez-moi de répéter: Julia n'est pas rapide, car le code est compilé à l'aide du compilateur JIT, mais le secret de la vitesse est que le code spécifique au type est compilé.
Si vous avez besoin d'une histoire complète, consultez certaines des notes que j'ai écrites pour le prochain séminaire . La spécificité de type est déterminée par le principe de base de la conception de Julia: la répartition multiple . Lorsque vous écrivez le code:
function f(a,b) return 2a+b end
Il semble que ce ne soit qu'une f(2.0,3.0) , Julia exécutera le code compilé, qui prend deux nombres à virgule flottante et renvoie 2a + b . Si vous appelez f(2,3) , Julia exécutera un autre code compilé qui prend deux entiers et renvoie 2a + b . La fonction f est une abstraction ou une abréviation pour de nombreuses méthodes différentes qui ont la même forme, et un tel schéma d'utilisation du symbole f pour appeler toutes ces différentes méthodes est appelé répartition multiple. Et cela s'applique partout: l'opérateur + est en fait une fonction qui appellera des méthodes en fonction des types qu'il voit. Julia obtient en fait sa vitesse car le code compilé par elle connaît ses types, et donc le code compilé qui appelle f (2.0,3.0) est exactement le code compilé que vous obtenez en définissant la même fonction dans C / Fortran . Vous pouvez vérifier cela avec la macro code_native pour voir l'assembly compilé:
@code_native f(2.0,3.0)
pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop
Il s'agit du même assembly compilé que vous attendez d'une fonction dans C / Fortran , et il diffère du code d'assembly pour les entiers:
@code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax)
Essence: REPL / Global Scope ne permet pas la spécificité de type
Cela nous amène au point principal: REPL / Global Scope est lent car il ne permet pas la spécification de type. Tout d'abord, notez que REPL est une portée globale car Julia autorise une portée imbriquée pour les fonctions. Par exemple, si nous définissons
function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end
nous verrons que ce code fonctionne. En effet, Julia vous permet de capturer
a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo()
et
a = 2; b = 3 ans2= linearcombo()
Question: Quels types le compilateur doit-il accepter pour a et b ? Notez que dans cet exemple, nous avons changé les types et appelé toujours la même fonction. Il peut traiter tous les types que nous y ajoutons: flottants, entiers, tableaux, types d'utilisateurs étranges, etc. Dans Julia, cela signifie que les variables doivent être encadrées et les types sont vérifiés chaque fois qu'ils sont utilisés. À votre avis, à quoi ressemble le code compilé?
Encombrant pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax)
Pour les langues dynamiques sans spécialisation de type, ce code gonflé avec toutes les instructions supplémentaires est aussi bon que possible, donc Julia ralentit à leur vitesse. Pour comprendre pourquoi c'est si important, notez que chaque morceau de code que vous écrivez dans Julia est compilé. Disons que vous écrivez une boucle dans votre script:
a = 1 for i = 1:100 a += a + f(a) end
Le compilateur devra compiler cette boucle, mais comme il ne peut garantir que les types ne changent pas, il enveloppe prudemment un footcloth sur tous les types, ce qui conduit à une exécution lente.
Comment éviter un problème
Il existe plusieurs façons d'éviter ce problème. Le moyen le plus simple consiste à toujours envelopper vos scripts dans des fonctions. Par exemple, le code précédent prendra la forme:
function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1)
Cela vous donnera le même résultat, mais comme le compilateur peut se spécialiser dans le type a , il fournira le code compilé que vous souhaitez. Une autre chose que vous pouvez faire est de définir vos variables comme constantes.
const b = 5
En faisant cela, vous dites au compilateur que la variable ne changera pas et qu'il pourra ainsi spécialiser tout le code qui l'utilise sur le type qu'elle est actuellement. Il y a une légère bizarrerie que Julia vous permet en fait de changer la valeur d'une constante, mais pas d'un type. Ainsi, vous pouvez utiliser const pour indiquer au compilateur que vous ne modifierez pas le type. Cependant, notez qu'il existe quelques petites bizarreries:
const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a
cela ne fonctionne pas comme prévu, car le compilateur, réalisant qu'il connaît la réponse à f () = a (puisque a est une constante), a simplement remplacé l'appel de fonction par la réponse, donnant un comportement différent de si a pas constant.
Moralité: n'écrivez pas vos scripts directement dans REPL, enveloppez-les toujours dans une fonction.
Nezhdanchik deux: Instabilité de type
Donc, je viens d'exprimer une opinion sur l'importance de la spécialisation du code pour les types de données. Permettez-moi de vous poser une question, que se passe-t-il lorsque vos types peuvent changer? Si vous avez deviné: «Eh bien, dans ce cas, vous ne pouvez pas spécialiser le code compilé», alors vous avez raison. Un tel problème est connu sous le nom d'instabilité de type. Ils peuvent apparaître différemment, mais un exemple courant est que vous initialisez la valeur avec le simple, mais pas nécessairement le type qu'elle devrait être. Par exemple, regardons:
function g() x=1 for i = 1:10 x = x/2 end return x end
Notez que 1/2 est un nombre à virgule flottante dans Julia. Par conséquent, si nous avons commencé avec x = 1 , l'entier changera en nombre à virgule flottante, et donc, la fonction devrait compiler la boucle interne, comme si elle pouvait être de n'importe quel type. Si à la place nous avions:
function h() x=1.0 for i = 1:10 x = x/2 end return x end
alors la fonction entière pourra compiler de manière optimale, sachant que x restera un nombre à virgule flottante (cette capacité pour le compilateur à déterminer les types s'appelle l'inférence de type). Nous pouvons vérifier le code compilé pour voir la différence:
Nappe native pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop
contre
Sort d'assembleur soigné pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax)
Une telle différence dans le nombre de calculs pour obtenir la même valeur!
Comment trouver et gérer l'instabilité de type

À ce stade, vous pouvez demander: "Eh bien, pourquoi ne pas simplement utiliser C pour ne pas avoir à rechercher ces instabilités?" La réponse est:
- Facile à trouver
- Ils peuvent être utiles.
Vous pouvez gérer l'instabilité avec des barrières fonctionnelles
Julia vous donne la macro code_warntype pour montrer où sont les instabilités de type. Par exemple, si nous utilisons ceci dans la fonction g , nous avons créé:
@code_warntype g()
obtenir l'analyse Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64}
Notez qu'au début, nous disons que le type x est Any . Il utilisera tout type qui n'est pas désigné comme strict type , c'est-à-dire qu'il s'agit d'un type abstrait qui doit être encadré / vérifié à chaque étape. Nous voyons qu'à la fin nous retournons x comme UNION {FLOAT64, INT64} , qui est un autre type non strict. Cela nous indique que le type code_warntype pour h , nous obtenons tous les types stricts:
@code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64
Cela indique que la fonction est de type stable et se compilera essentiellement dans un code C optimal. Ainsi, l'instabilité de type n'est pas difficile à trouver. Le plus difficile est de trouver le bon design. Pourquoi résoudre l'instabilité de type? Il s'agit d'un problème de longue date qui a conduit au fait que les langages typés dynamiquement dominent le terrain de jeu des scripts. L'idée est que dans de nombreux cas, vous voulez trouver un compromis entre performances et fiabilité.
Par exemple, vous pouvez lire un tableau à partir d'une page Web dans laquelle des entiers sont mélangés avec des nombres à virgule flottante. Dans Julia, vous pouvez écrire votre fonction de sorte que si tous étaient des entiers, elle se compile bien, et si tous étaient des nombres à virgule flottante, elle se compile également bien. Et s'ils sont mélangés? Cela fonctionnera toujours. C'est la flexibilité / commodité que nous connaissons et aimons d'un langage comme Python / R. Mais Julia vous dira directement ( via code_warntype ) lorsque vous sacrifiez les performances.
Comment gérer les instabilités de type
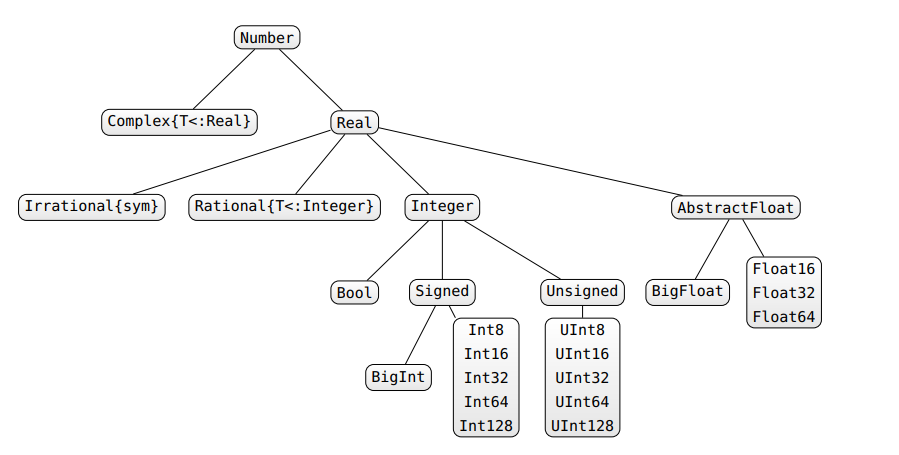
Il existe plusieurs façons de gérer les instabilités de type. Tout d'abord, si vous aimez quelque chose comme C / Fortran où vos types sont déclarés et ne peuvent pas changer (ce qui garantit la stabilité du type), vous pouvez le faire dans Julia:
local a::Int64 = 5
Cela fait a entier 64 bits, et si un code futur essaie de le changer, un message d'erreur sera généré (ou la conversion correcte sera effectuée. Mais puisque la conversion ne sera pas automatiquement arrondie, elle provoquera très probablement des erreurs). Saupoudrez-les autour de votre code et vous obtenez la stabilité du type, ala, C / Fortran . Une manière moins compliquée de gérer cela est avec les instructions de type. Ici, vous mettez la même syntaxe de l'autre côté du signe égal. Par exemple:
a = (b/c)::Float64
Il semble dire: "calculez b / c et assurez-vous que la sortie est Float64. Si ce n'est pas le cas, essayez d'effectuer une conversion automatique. Si la conversion ne peut pas être facilement effectuée, émettez une erreur." Le placement de ces conceptions vous aidera à vous assurer que vous savez quels types sont impliqués. Cependant, dans certains cas, l'instabilité de type est nécessaire. Par exemple, disons que vous voulez avoir un code fiable, mais l'utilisateur vous donne quelque chose de fou, comme:
arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1
qui est un tableau d'entiers 4x1 et de nombres à virgule flottante. Le type d'élément réel pour le tableau est Union {Int64, Float64} , ce qui, comme nous l'avons vu précédemment, n'était pas strict, ce qui pouvait entraîner des problèmes. Le compilateur sait seulement que chaque valeur peut être un entier ou un nombre à virgule flottante, mais pas quel élément de quel type. Cela signifie qu'il est naïf de faire de l'arithmétique avec ce tableau, par exemple:
function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end
sera lent puisque les opérations seront encadrées. Cependant, nous pouvons utiliser plusieurs répartitions pour exécuter des codes de manière spécialisée. C'est ce que l'on appelle l'utilisation de barrières fonctionnelles. Par exemple:
function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end
Notez qu'en raison de la répartition multiple, l'appel à inner_foo appelle soit une méthode spécialement compilée pour les nombres à virgule flottante, soit une méthode spécialement compilée pour les nombres entiers. Ainsi, vous pouvez mettre un long calcul dans inner_foo et le faire toujours bien fonctionner, pas inférieur au typage strict que la barrière fonctionnelle vous donne.
Ainsi, j'espère que vous voyez que Julia offre une bonne combinaison de performances de frappe solides et de la commodité de la frappe dynamique. Un bon programmeur, Julia, a les deux options pour maximiser la productivité et / ou la productivité si nécessaire.
Surprise 3: Eval fonctionne à l'échelle mondiale

L'une des plus grandes forces de Julia est ses capacités de métaprogrammation. Cela vous permet d'écrire facilement des programmes générant du code, ce qui réduit efficacement la quantité de code dont vous avez besoin pour écrire et maintenir. Une macro est une fonction qui s'exécute au moment de la compilation et (généralement) crache du code. Par exemple:
macro defa() :(a=5) end
remplacera toute instance defa par le code a = 5 ( :(a = 5) est une expression citée . Le code de Julia est des expressions, et donc la métaprogrammation est une collection d'expressions).
Vous pouvez l'utiliser pour construire n'importe quel programme Julia complexe que vous souhaitez et le mettre dans une fonction comme un type de raccourci vraiment intelligent. Cependant, vous devrez parfois évaluer directement le code généré. Julia vous donne une fonction eval ou @eval macro @eval pour ce faire. En général, vous devriez essayer d'éviter eval , mais il y a certains codes où il est nécessaire, par exemple, ma nouvelle bibliothèque pour transférer des données entre différents processus pour une programmation parallèle . , , :
@eval :(a=5)
(REPL). , / . Par exemple:
function testeval() @eval :(a=5) return 2a+5 end
, a REPL. , , :
function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end
b — , , , , , . eval , , REPL .
4:
Julia , . : , .
, ? , , . Par exemple:
a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a
, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :
a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13
90, . , .
. — , . rssdev10
. Par exemple:
x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)]
, a b — , ! (2,2) , — (1-) 2. , , :
a = [1 -2] b = [1 - 2]
: 1 -2 . : 1-2 . - . :
a = [1 2 3 -4 2 -3 1 4]
2x4. , . : hcat :
a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4))
!
№5: ,

(View) — () , ( ), .
, , . , . , .
— "". ""
a = [3;4;5] b = a b[1] = 1
, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :
a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array
b , b a , b . , , ( , ). . , . Par exemple:
c = a[1:2,1]
c a ). , , , , . , , :
d = @view a[1:2,1] e = view(a,1:2,1)
d , e — , d e a , , , reshape , .) , . Par exemple:
a[1:2,1] = [1;2]
a , a[1:2,1] view (a, 1:2,1) , , a . -? , :
b = copy(a)
, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :
a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ]
b = copy(a) b[1][1] = 10 a
3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9]
, a[1][1] 10! ? copy a . a , b , b . , deepcopy :
b = deepcopy(a)
, . , , .
№6: , In-Place
MATLAB / Python / R . Julia , , , " ".
function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end
, inner , , 2x . , . , - y , :
function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end
. inner!(y, x) , y . y , y , , , inner! (y, x) ! ( ).
, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .
, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), f.(x) — , f x , , . f x , x = x + f. (x) . :
x .= x .+ f.(x)
.= , , ,
for i = 1:length(x) x[i] = x[i] + f(x[i]) end
, :
function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end
MATLAB / R / Python , , , .
: ,
: , . , . , . , , . , .
- , C / Fortran , . - , , !
: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]