Présentation:Un grand nombre des problèmes les plus divers concernant presque toutes les branches les plus importantes de la physique mathématique et conçus pour répondre à des questions techniques d'actualité est associé à l'application des fonctions de Bessel.
Les fonctions de Bessel sont largement utilisées pour résoudre des problèmes d'acoustique, de radiophysique, d'hydrodynamique, des problèmes de physique atomique et nucléaire. Nombreuses applications des fonctions de Bessel à la théorie de la conductivité thermique et à la théorie de l'élasticité (problèmes de vibrations des plaques, problèmes de théorie des coques, problèmes de détermination de la concentration de contraintes près des fissures).
Cette popularité des fonctions de Bessel s'explique par le fait que la résolution d'équations de physique mathématique contenant l'opérateur de Laplace en coordonnées cylindriques par la méthode classique de séparation des variables conduit à une équation différentielle ordinaire, qui sert à déterminer ces fonctions [1].
Les fonctions de Bessel sont nommées d'après l'astronome allemand Friedrich Bessel, qui en 1824, étudiant le mouvement des planètes autour du soleil, a dérivé les relations de récurrence des fonctions de Bessel
Jv(x) reçu pour des entiers
v représentation intégrale d'une fonction
Jv(x) , a prouvé l'existence d'innombrables zéros de fonction
J0(x) et compilé les premières tables de fonctions
J1(x) et
J2(x) .
Cependant, pour la première fois l'une des fonctions de Bessel
J0(x) Il a été envisagé en 1732 par Daniel Bernoulli dans un ouvrage consacré à l'oscillation des chaînes lourdes. D. Bernoulli a trouvé une expression de fonction
J0(x) sous la forme d'une série de puissance et a remarqué (sans preuve) que l'équation
J0(x)=0 a d'innombrables racines valides.
L'ouvrage suivant, dans lequel se rencontrent les fonctions de Bessel, est celui de Léonard Euler en 1738, consacré à l'étude des vibrations d'une membrane circulaire. Dans ce travail, L. Euler a trouvé des entiers
v Expression de la fonction de Bessel
Jv(x) sous la forme d'une série de pouvoirs
x , et dans des articles ultérieurs ont étendu cette expression au cas des valeurs d'index arbitraires
v . En outre, L. Euler a prouvé que, pour
v égal à un entier et demi, fonctions
Jv(x) exprimée à travers les fonctions élémentaires.
Il a noté (sans preuve) qu’avec une
v les fonctions
Jv(x) ont d'innombrables vrais zéros et ont donné une représentation intégrale pour
Jv(x) . Certains chercheurs pensent que les principaux résultats liés aux fonctions de Bessel et à leurs applications en physique mathématique sont liés au nom de L. Euler.
Étudier la propriété des fonctions de Bessel et en même temps maîtriser les méthodes de résolution d'équations réduites aux fonctions de Bessel, permet le programme librement distribué de mathématiques symboliques SymPy - la bibliothèque Python.
Dans le programme de mathématiques symboliques SymPy, des graphiques des fonctions de Bessel du premier type d'ordres entiers peuvent être construits en utilisant la relation pour la somme d'une série:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm! Gamma(p+m+1)
Fonctions de Bessel du premier typefrom sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
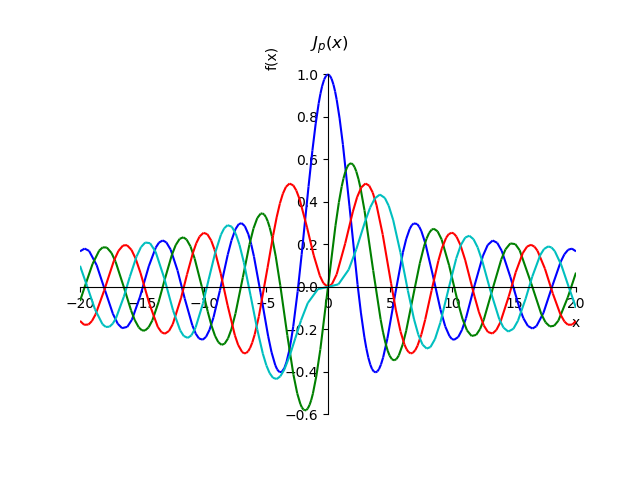
En utilisant la relation pour la somme d'une série, nous pouvons prouver la propriété de ces fonctions pour des commandes entières
J1(x)=−J−1(x):
Propriété de la fonction Bessel du premier type from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

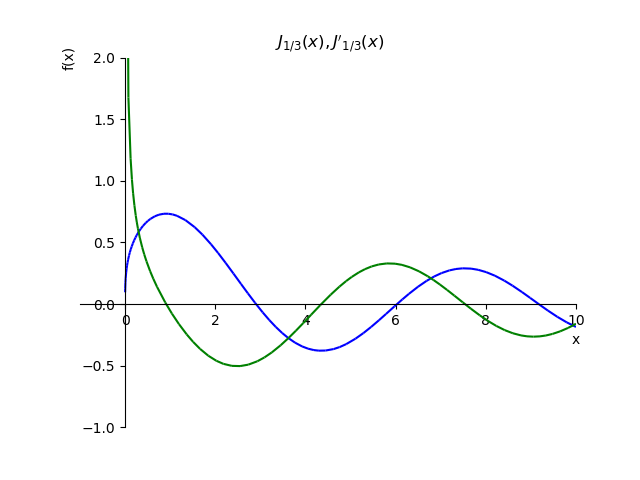
Pour démontrer les conditions de Cauchy, nous construisons une fonction
J1/3(x) et son dérivé
fracdJ1/3(x)dx: :
Fonction d'ordre fractionnaire et sa dérivée from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
Cependant, pour les calculs pratiques, le merveilleux module mpmath est utilisé, qui permet non seulement de résoudre numériquement des équations avec des fonctions de Bessel du premier et du deuxième type, y compris des modifications de tous les ordres admissibles, mais également de construire des graphiques avec une mise à l'échelle automatique.
De plus, le module mpmath ne nécessite pas d'outils spéciaux pour partager des mathématiques symboliques et numériques. L'histoire de la création de ce module et la possibilité de son utilisation pour la transformée de Laplace inverse que j'ai déjà considérée dans la publication [2]. Nous continuons maintenant la discussion de mpmath pour travailler avec les fonctions de Bessel [3].
Fonction de Bessel du premier type JN(x)mpmath.besselj (n, x, dérivée = 0) - donne une fonction de Bessel du premier type
Jn(x) . Les fonctions
JN(x) est une solution à l'équation différentielle suivante:
x2y″+xy′+(x2−n2)y=0
Pour l'ensemble positif
n se comporte comme un sinus ou un cosinus, multiplié par un coefficient qui diminue lentement avec
x rightarrow pm inftyFonction de Bessel du premier type
JN(x) est un cas particulier de fonction hypergéométrique
oF1 :
Jn(x)= fracxn2n Gamma(n+1)oF1(n+1, fracx24)
La fonction de Bessel peut être différenciée
m fois à condition que la mième dérivée ne soit pas égale à zéro:
fracdmdxmJn(x)
Fonction de Bessel du premier type
JN(x) pour les ordres entiers positifs n = 0,1,2,3 - la solution de l'équation de Bessel:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

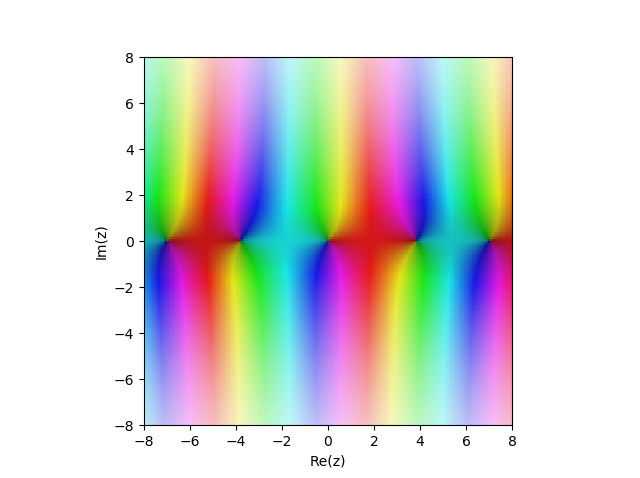
Fonction de Bessel du premier type
JN(x) dans le plan complexe:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
Exemples:
Fonction
besselj(N,x) fournit un résultat avec un nombre donné de chiffres
(mp.dps) après une virgule:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
Un argument de fonction peut être un grand nombre:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
Les fonctions de Bessel du premier type satisfont des symétries simples par rapport à
x=0 :
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
Les racines ne sont pas périodiques, mais la distance entre les racines successives se rapproche asymptotiquement
2π . Les fonctions de Bessel du premier type ont le code suivant:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
Pour
n=1/2 ou
n=−1/2 La fonction de Bessel est réduite à une fonction trigonométrique:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
Les dérivés de n'importe quel ordre peuvent être calculés,
les ordres négatifs correspondent à l'intégration :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
La différenciation avec un ordre non entier donne une dérivée fractionnelle au sens de l'intégrale différentielle de Riemann-Liouville, calculée à l'aide de la fonction
difint() :
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
Autres façons d'appeler la fonction de Bessel du premier type de zéro et de premier ordre
mpmath.j0 (x) - Calcule la fonction Bessel
J0(x) ;
mpmath.j1 (x) - Calcule la fonction Bessel
J1(x) ;
Fonctions de Bessel du second typebessely (n, x, dérivée = 0) Calcule la fonction de Bessel de second type à partir de la relation:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
Pour un entier
n La formule suivante doit être comprise comme la limite. La fonction de Bessel peut être différenciée
m fois à condition que la mième dérivée ne soit pas égale à zéro:
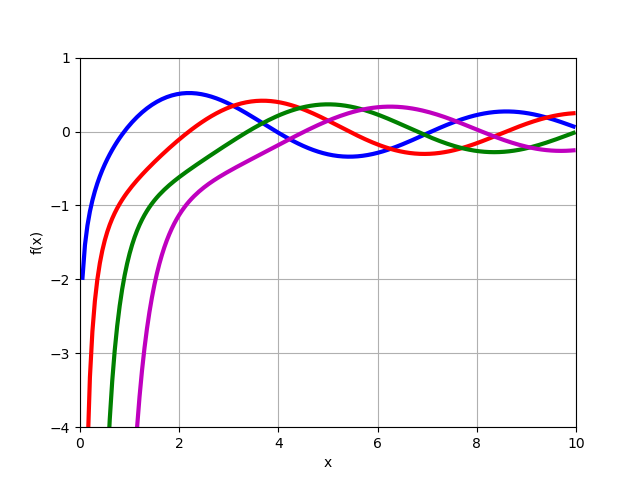
fracdmdxmYn(x)Fonction de Bessel du second type
Yn(x) pour les ordres positifs entiers
n=0,1,2,3 .
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
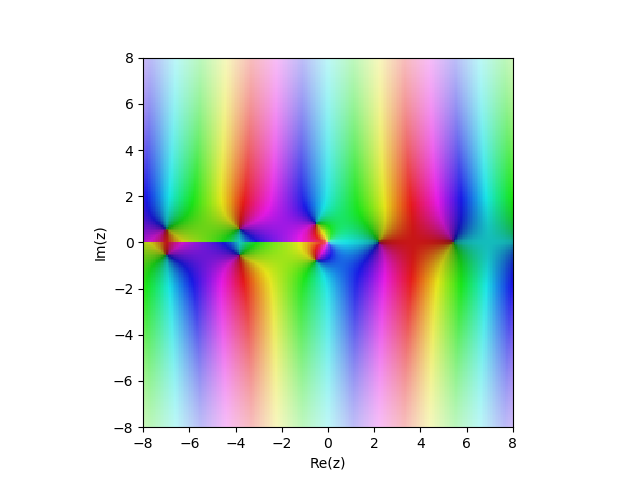
2ème fonction Bessel
Yn(x) dans le plan complexe
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
Exemples:
Certaines valeurs de fonction
Yn(x) :
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
Les arguments peuvent être volumineux:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
Les dérivés de tout ordre, y compris négatifs, peuvent être calculés:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
Fonction Bessel modifiée du premier type
mpmath.besseli(n, x, derivative=0)
besseli (n, x, dérivée = 0) fonction de Bessel modifiée du premier type
In(x)= mathiti−nJn(ix)
fracdmdxmIn(x)
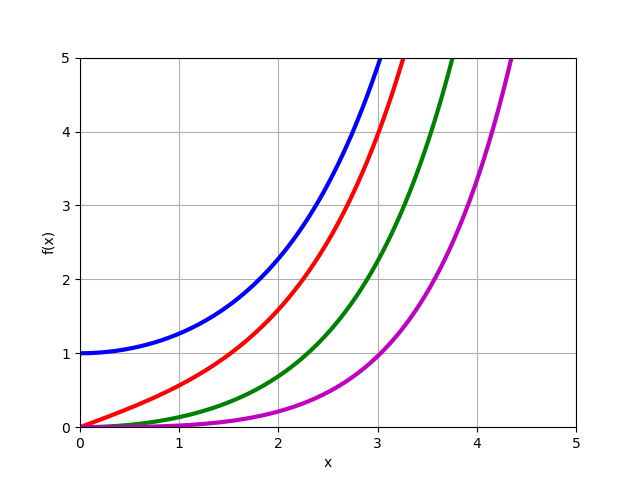
Fonction Bessel modifiée
In(x) pour les commandes réelles
n=0,1,2,3 :
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
Fonction Bessel modifiée
In(x) dans le plan complexe
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

Exemples:
Quelques significations
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
Les arguments peuvent être volumineux:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
Pour les entiers n, la représentation intégrale suivante est vraie:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
Les dérivés de toute commande peuvent être calculés:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
Fonctions Bessel modifiées du second type,
mpmath.besselk(n, x)
besselk (n, x) fonctions de Bessel de second type modifiées
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
Pour un entier
n cette formule doit être comprise comme une limite.
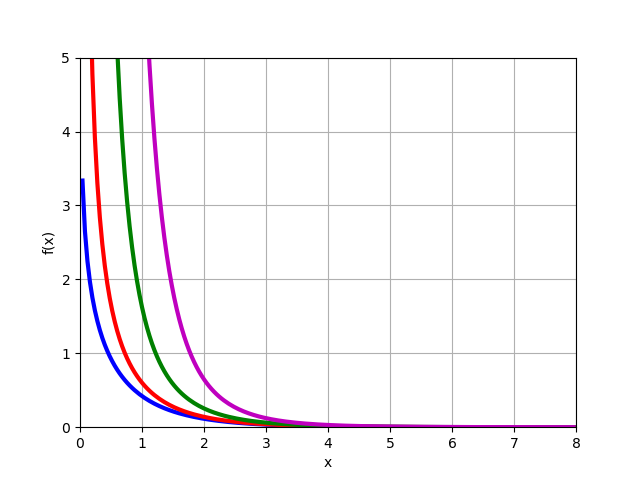
Fonction Bessel modifiée du 2e type
Kn(x) pour le matériel
n=0,1,2,3 :
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
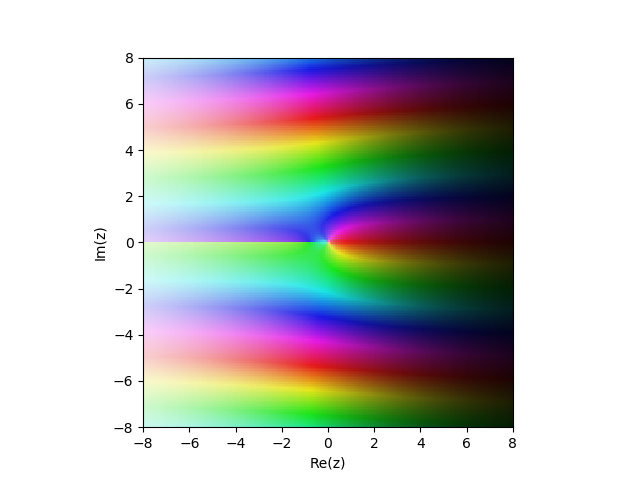
Fonction Bessel modifiée du 2e type
Kn(x)) dans le plan complexe
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
Exemples:
Arguments compliqués et complexes:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
Les arguments sont de grands nombres
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
Caractéristiques du comportement d'une fonction en un point
x=0 :
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
Bessel Function Zeros besseljzero() mpmath.besseljzero(v, m, derivative=0)
Pour une commande réelle
mathit nu geq0 et un entier positif
m retourne
j nu,m , le mième zéro positif de la fonction de Bessel du premier type
J nu(z) (voir
besselj () ). Alternativement, avec
dérivé=1 donne le premier zéro premier non négatif
j′ nu,m de
J′ nu(z) . Indexation des désignations des accords à l'aide d'Abramowitz & Stegun et DLMF. Faites attention à un cas spécial.
j′0,1=0 tandis que tous les autres zéros sont positifs.
En réalité, seuls les zéros simples sont calculés (tous les zéros des fonctions de Bessel sont simples, sauf lorsque
z=0 ) et
j nu,m devient une fonction monotone de
nu et
m . Les zéros alternent selon les inégalités:
j′ nu,k<j nu,k<j′ nu,k+1
j nu,1<j nu+1,2<j nu,2<j nu+1,2<j nu,3 cdots
Exemples:
Zéros de tête des fonctions de Bessel
J0(z) ,
J1(z) ,
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
Zéros de tête des dérivées des fonctions de Bessel
J′0(z) ,
J′1(z) ,
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
Zéros avec un grand index:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
Zéros de fonctions avec une commande importante:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
Zéros de fonctions avec ordre fractionnaire:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
Et
J nu(z) . et
J′ nu(z) peuvent être exprimés comme des produits infinis à leurs zéros:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
Pour une commande réelle
mathit nu geq0 et un entier positif
m retourne
y nu,m ,
m , mième zéro positif du second type de fonction de Bessel
Y nu(z) (voir
Bessely () ). Alternativement, avec
dérivé=1 donne le premier zéro positif
y′ nu,m de
Y′ nu(z) . Les zéros alternent selon les inégalités:
y nu,k<y′ nu,k<y nu,k+1
y nu,1<y nu+1,2<y nu,2<y nu+1,2<y nu,3 cdots
Exemples:
Zéros de tête des fonctions de Bessel
Y0(z) ,
Y1(z) ,
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
Zéros de tête des dérivées des fonctions de Bessel
Y′0(z) ,
Y′1(z) ,
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
Zéros avec un grand index:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
Zéros de fonctions avec une commande importante:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
Zéros de fonctions avec ordre fractionnaire:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
Applications de la fonction BesselL'importance des fonctions de Bessel est due non seulement à l'apparition fréquente de l'équation de Bessel dans les applications, mais aussi au fait que les solutions de nombreuses autres équations différentielles linéaires du second ordre peuvent être exprimées en termes de fonctions de Bessel. Pour voir comment ils apparaissent, nous commençons par l'équation de Bessel
p sous forme de:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0,(1)
et remplacer ici
w=x− alpha,z=kx beta,(2)
Ensuite, en utilisant (2) et en introduisant les constantes
A,B,C à partir de l'équation (1), on obtient:
x2y″+Axey′+(B+Cxq)y=0,(3)
A=1−2 alpha,B= alpha2− beta2p2,C= beta2k2,q=2 beta,(4)
De l'équation (4) nous obtenons:
\ left \ {\ begin {matrix} \ alpha = \ frac {1-A} {2}, \\ \ beta = \ frac {q} {2}, \\ k = \ frac {2 \ sqrt {C }} {q} \\ p = \ frac {\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {matrix} \ right. (5)
Si
C>0 ,
q neq0 ,
(1−A)2 geqslant4B , alors la solution générale (pour
x>0 ) de l'équation (3) a la forme:
y(x)=x alpha left[c1Jp(kx beta)+c2J−p(kx beta) droite](6)
où:
alpha ,
beta ,
k sont déterminés à partir du système (5). Si
p Est un entier alors
Jp doivent être remplacés par
Yp .
Flexion longitudinale de la colonne verticaleNous allons maintenant considérer une tâche qui est importante pour les applications pratiques. Dans cette tâche, il est nécessaire de déterminer quand une colonne verticale uniforme est pliée sous son propre poids. Nous supposons
x=0 dans l'extrémité supérieure libre de la colonne et
x=L>0 à sa base; nous supposons que la base est insérée de manière rigide (c'est-à-dire fixe immobile) dans la base (dans le sol), éventuellement dans du béton.
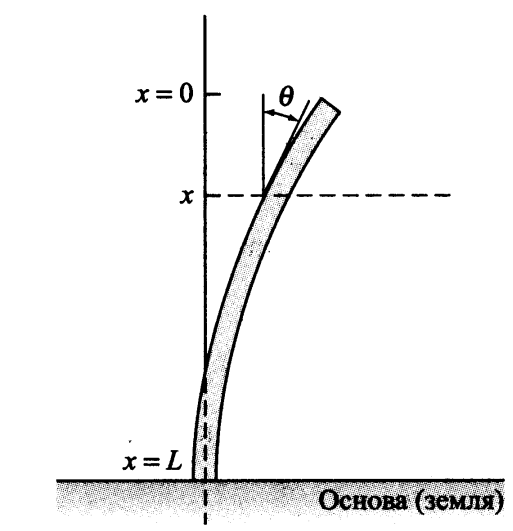
Indique l'écart angulaire de la colonne au point
x à travers
thêta(x) . De la théorie de l'élasticité dans ces conditions, il résulte que:
EI fracd2 thetadx2+g rhox theta=0,(7)
où
E - module d'Young du matériau de la colonne,
I - moment d'inertie de sa section,
rho - densité linéaire de la colonne et
g - accélération gravitationnelle. Les conditions aux limites sont de la forme:
theta′(0)=0, theta(L)=0,(8)
Nous allons résoudre le problème en utilisant (7) et (8) avec:
lambda= gamma2= fracg rhoEI(9)
On réécrit (7) en prenant en compte (9) sous condition (8):
fracd2 thetadx2+ gamma2x theta=0; fracd thetadx=0, theta(L)=0.(10)
Une colonne ne peut être déformée que s'il existe une solution non triviale au problème (10); sinon, la colonne restera dans une position non déviée de la verticale (c'est-à-dire physiquement incapable de dévier de la verticale).
L'équation différentielle (10) est une équation d'Airy. L'équation (10) a la forme de l'équation (3) pour
A=B=0 ,
C= gamma2 ,
q=3 . Du système d'équations (5) on obtient
alpha= frac12 ,
beta= frac32 ,
k= frac23 gamma ,
p= frac13 .
Par conséquent, la solution générale a la forme:
theta(x)=x1/2 left[c1J1/3( frac23 gammax3/2)+c2J−1/3( frac23 gammax3/2) droite].(11)
Pour appliquer les conditions initiales, nous substituons
p= pm frac13 dans
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1) left( fracx2 droite)2m+p(12)
Après transformation (12), en tenant compte de la solution (11), on obtient:
theta(x)= fracc1 gamma1/331/3 Gamma(4/3) left(x− frac gamma2x412+ frac gamma4x7504− cdot cdot cdot right)++ fracc231/3 gamma1/3 Gamma( frac23) left(1− frac gamma2x36+ frac gamma4x6180− cdot cdot cdot right).(13)
Fourni au point de départ
theta′(0)=0 nous obtenons
c1=0 , alors (11) prend la forme:
theta(x)=c2x1/2J−1/3( frac23 gammax3/2),(14)
Fourni au point final
thêta(L)=0 , de (14) on obtient:
J−1/3( frac23 gammaL3/2)=0(15)
Il convient de noter que les transformations (13), (14) ne pourraient pas être faites si nous traçions les fonctions
J1/3(x),J−1/3(x) en utilisant les capacités considérées du module mpmath:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
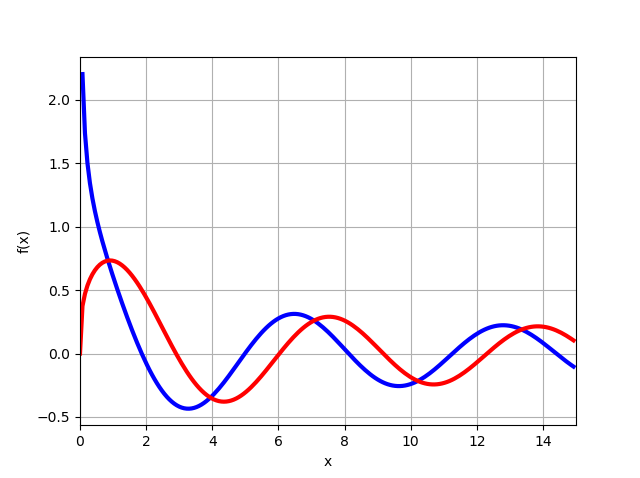
Il ressort du graphique que pour x = 0, la fonction
J1/3(0)=0 et compte tenu de la solution (11), on obtient immédiatement l'équation (15) nécessaire, il ne reste plus qu'à trouver z, comme on le verra plus loin.
Ainsi, la colonne n'est déformée que si
z= frac23 gammaL3/2 Est la racine de l'équation
J−1/3(z)=0 . Créer une fonction
J−1/3(z) sur un graphique séparé:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

Le graphique montre que la première racine est légèrement inférieure à 2. Trouver la racine
z0 de l'équation
J−1/3(z)=0 Vous pouvez, en utilisant la fonction
findroot (f, z0) , accepter, selon le graphique, le point de recherche
x0=1 et six décimales
mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
Nous obtenons:
z0=1,86635Nous calculons la longueur critique, par exemple, un mât de drapeau, en utilisant la formule (15):
Hauteur du mât pour différents paramètres dans la section from numpy import* def LRr(R,r): E=2.9*10**11
Nous obtenons:
8,47 m
10,25 m
Un mât creux peut être plus haut qu'un mât plein.
Propagation des vagues dans une membrane mince.
Une fine membrane lorsque les ondes sonores y pénètrent non seulement oscille avec la fréquence des ondes. La forme des vibrations membranaires peut être obtenue dans les fonctions de Bessel selon la liste suivante, en utilisant les formules
besselj () et
besseljzero () :
Forme d'onde de la membrane from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()
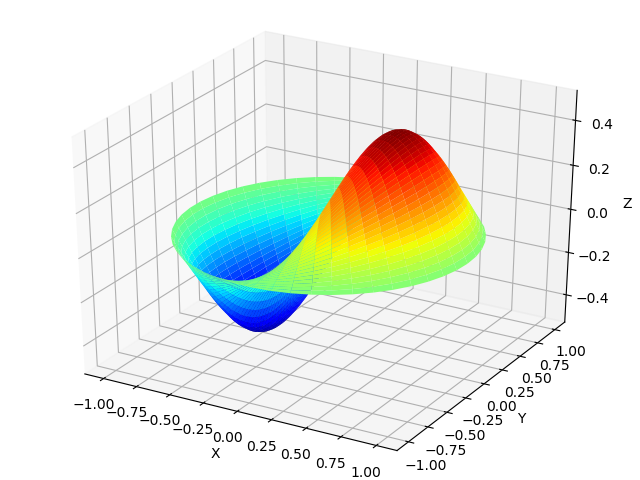
Alternative au module mpmath dans les fonctions spéciales Bessel de la bibliothèque SciPy
Sans me plonger dans une discussion détaillée des fonctions de Bessel de la bibliothèque SciPy [4], je ne donnerai que deux listes pour tracer des fonctions des premier et deuxième types
jv (v, x) ,
yv (v, x) :
jv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
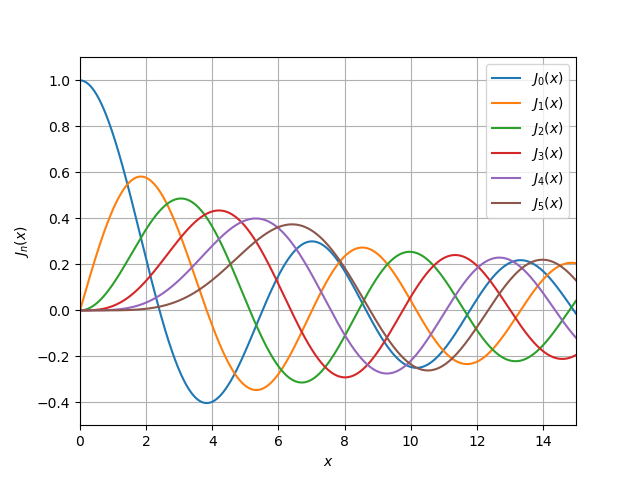
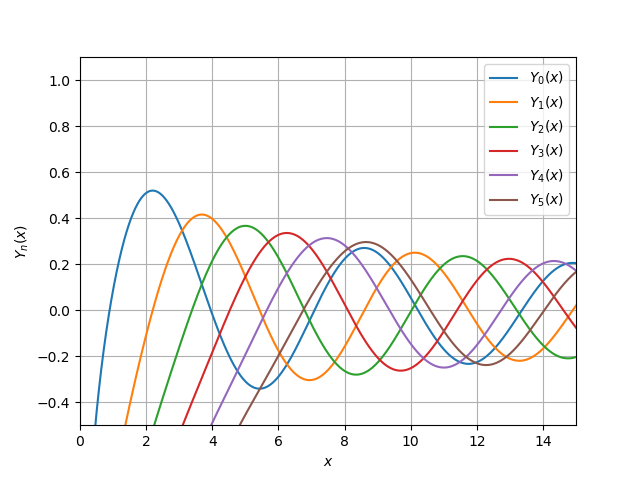
yv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()
Conclusions:
L'article décrit les bases de l'utilisation des fonctions de Bessel à l'aide des bibliothèques mpmath, sympy et scipy, fournit des exemples d'utilisation de fonctions pour résoudre des équations différentielles. L'article peut être utile pour étudier les équations de la physique mathématique.
Références:
1.
Fonctions Bessel2.
Utilisation de la transformée de Laplace inverse pour analyser les liens dynamiques des systèmes de contrôle3.
Fonctions liées à la fonction de Bessel4.
Fonctions spéciales (scipy.special).