La conversion de modèles à la volée est une pratique courante pour simuler la physique des déformations, ainsi que dans les jeux avec un contenu généré dynamiquement et modifiable. Dans de tels cas, il est pratique d'appliquer des méthodes d'édition procédurale et de création de géométrie. Ces derniers permettent souvent d'économiser des octets précieux lors de la transmission de données téléchargées depuis le réseau. De plus, c'est amusant!
L'article vise à pomper les compétences du traitement procédural des maillages dans Unity. Nous parlerons des opérations de transformation et de génération de parties d'un maillage.
Notre kit gentlemanly pour l'édition procédurale de modèles 3D comprend trois opérations de base: triangulation, déplacement de points, extrusion. Nous parlerons en détail des deux derniers. Tout d'abord, considérez les opérations de mouvement les plus simples - déplacement des sommets, rotation et mise à l'échelle des arêtes et des triangles. Ensuite, nous traiterons de l'une des méthodes de génération d'une nouvelle géométrie - l'opération d'extrusion.
Dans une publication précédente, nous avons décrit notre structure pour un travail pratique avec les données des modèles 3D.Code de structurepublic static class CustomMeshPool { private static List<CustomMesh> Pool; private static int pointer; public static CustomMesh GetMesh(int id) { return Pool[id]; } public static int Push(CustomMesh customMesh) { if (Pool == null) Pool = new List<CustomMesh>(); pointer = GetAvailableIndex(); if (pointer < Pool.Count) Pool[pointer] = customMesh; else Pool.Add(customMesh); return pointer; } public static bool Remove(int index) { if (Pool == null) return false; var b = Pool[index] == null; Pool[index] = null; return b; } public static int GetAvailableIndex() { if (Pool == null) return 0; var availableIndex = Pool.FindIndex(mesh => mesh == null); return availableIndex != -1 ? availableIndex : Pool.Count; } public static void Flush() { if (Pool != null) Pool.Clear(); } } public class CustomMesh { public int Id; public Triangle[] Triangles; public Vector3[] vertices; public Vector3[] normals; public Vector2[] uv0, uv2; public Color[] colors; public CustomMesh(Vector3[] vertices, int[] triangles, Vector3[] normals, Vector2[] uv0, Vector2[] uv2, Color[] colors) { this.vertices = vertices; this.normals = normals; if (normals != null) for (var i = 0; i < this.normals.Length; i++) { this.normals[i] = this.normals[i].normalized; } this.uv0 = uv0; this.uv2 = uv2; this.colors = colors; var ptr = CustomMeshPool.GetAvailableIndex(); CustomMeshPool.Push(this); Id = ptr; Triangles = new Triangle[triangles.Length / 3]; Triangles = Triangles .AsParallel() .Select((t, i) => new Triangle(ptr, i, triangles[i * 3], triangles[i * 3 + 1], triangles[i * 3 + 2])) .ToArray(); } } public struct Triangle { private int _index; public int Index { get { return _index; } set { _index = value; if (_edges != null) { _edges[0].TriangleIndex = value; _edges[1].TriangleIndex = value; _edges[2].TriangleIndex = value; } } } private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private Edge[] _edges; public Edge[] Edges { get { return _edges; } set { if (value.Length == 3) { _edges = value; for (var i = 0; i < 3; i++) { _edges[i].TriangleIndex = _index; } } else throw new IndexOutOfRangeException(); } } public Vertex V0 { get { return Edges[0].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[0].v0 = value; Edges[2].v1 = value; } } public Vertex V1 { get { return Edges[1].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[1].v0 = value; Edges[0].v1 = value; } } public Vertex V2 { get { return Edges[2].v0; } set { if (value.MeshId != MeshId) throw new Exception("Not the same mesh"); Edges[2].v0 = value; Edges[1].v1 = value; } } public Triangle(int meshId, int index, int v0, int v1, int v2) { _index = index; _meshId = meshId; var edges = new Edge[3]; edges[0] = new Edge(meshId, index, v0, v1); edges[1] = new Edge(meshId, index, v1, v2); edges[2] = new Edge(meshId, index, v2, v0); _edges = edges; } } public struct Edge { public Vertex v0; public Vertex v1; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } private int _triangleIndex; public int TriangleIndex { get { return _triangleIndex; } internal set { _triangleIndex = value; } } public Edge(int meshId, int triangleIndex, int v0Index, int v1Index) { _meshId = meshId; _triangleIndex = triangleIndex; v0 = new Vertex() { MeshId = meshId, Index = v0Index }; v1 = new Vertex() { MeshId = meshId, Index = v1Index }; } } public struct Vertex { public int Index; private int _meshId; public int MeshId { get { return _meshId; } internal set { _meshId = value; } } public Vector3 position { get { return CustomMeshPool.GetMesh(_meshId).vertices[Index]; } set { CustomMeshPool.GetMesh(_meshId).vertices[Index] = value; } } public Vector3 normal { get { return CustomMeshPool.GetMesh(_meshId).normals[Index]; } set { CustomMeshPool.GetMesh(_meshId).normals[Index] = value; } } public Vector2 uv0 { get { return CustomMeshPool.GetMesh(_meshId).uv0[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv0[Index] = value; } } public Vector2 uv2 { get { return CustomMeshPool.GetMesh(_meshId).uv2[Index]; } set { CustomMeshPool.GetMesh(_meshId).uv2[Index] = value; } } public Color color { get { return CustomMeshPool.GetMesh(_meshId).colors[Index]; } set { CustomMeshPool.GetMesh(_meshId).colors[Index] = value; } } }
Comme vous pouvez le voir, PLINQ est utilisé ici. En effet, les algorithmes de géométrie de calcul peuvent souvent être optimisés par le multithreading.
Bien sûr, plus de constructions LINQ sont créées pendant l'exécution de constructions LINQ que lorsque le code «manuel» est exécuté. Cependant, cet inconvénient est largement compensé par la brièveté de ces conceptions, ainsi que par la présence d'outils intégrés de gestion des ressources dans PLINQ. De plus, la transition entre les implémentations monothread et multithread s'effectue avec une seule commande, ce qui facilite grandement le processus de débogage.Je tord, tord, je veux confondre
Nous procédons aux opérations du mouvement. Il n'y a rien de compliqué à déplacer des sommets. N'oubliez pas les pics coïncidents: si nécessaire, leur position devrait également changer.
L'algorithme est implémenté en ajoutant un vecteur de mouvement à la position du sommet. Le décalage se produit par rapport à l'origine du modèle (
pivot ). Il est à noter que la position des polygones lors de telles transformations peut changer, mais pas les normales de leurs sommets. Cependant, pour simplifier la présentation, nous ne considérerons pas cette nuance.
Les outils de CAO ont une fonction pour recalculer les normales, qui est généralement appelée après avoir appliqué les transformations requises. Il existe différentes façons de procéder à cette allocation. La plus courante calcule la normale au plan de chaque triangle, puis attribue une normale à chaque sommet comme moyenne des normales des triangles auxquels ce sommet appartient.En général, il n'y a aucune bonne raison de compliquer le code et d'appliquer la matrice de transformation. Le résultat de l'ajout d'un vecteur de mouvement à la position du sommet correspond à une idée intuitive de son mouvement.
| 
|
Liste des méthodes pour déplacer un sommet public struct Vertex { ... public void Translate(Vector3 movement, bool withCoincident = false) { var newPosition = position + movement; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var mask = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(position); for (int i = 0; i < vertices.Length; i++) if (mask[i]) vertices[i] = newPosition; } else { position = newPosition; } } } public class CustomMesh { … public bool[] GetVerticesInPosition(Vector3 position) { bool[] buffer = new bool[vertices.Length]; for (int i = 0; i < buffer.Length; i++) { buffer[i] = Mathf.Abs(position.x - vertices[i].x) < Mathf.Epsilon && Mathf.Abs(position.y - vertices[i].y) < Mathf.Epsilon && Mathf.Abs(position.z - vertices[i].z) < Mathf.Epsilon; } return buffer; } }
Le mouvement des arêtes et des triangles est mis en œuvre de la même manière - en ajoutant un vecteur de déplacement.
Liste des méthodes de déplacement des triangles et des arêtes public struct Edge { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var newV0Position = v0.position + movement; var newV1Position = v1.position + movement; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.Translate(movement); v1.Translate(movement); } } } public struct Triangle { … public void Translate(Vector3 movement, bool withCoincident = false) { if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var newV0Position = V0.position + movement; var newV1Position = V1.position + movement; var newV2Position = V2.position + movement; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { V0.Translate(movement); V1.Translate(movement); V2.Translate(movement); } } }
Mais il est plus pratique de faire pivoter et de mettre à l'échelle à
l' aide de
la matrice de transformation . Le résultat de l'exécution de ces opérations par rapport à l'origine des coordonnées du modèle ne sera probablement pas ce que vous attendiez ou vouliez voir. Le point de référence de rotation et de mise à l'échelle est généralement considéré comme le milieu de l'objet - comme le plus compréhensible pour l'homme.
Liste des méthodes de rotation et de mise à l'échelle des triangles et des bords public struct Edge { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (v0.position + v1.position) * 0.5f; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(v0.position - pivot); var newV1Position = matrix.MultiplyPoint(v1.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(MeshId).vertices; var maskV0 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v0.position); var maskV1 = CustomMeshPool.GetMesh(MeshId).GetVerticesInPosition(v1.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; } } else { v0.position = newV0Position; v1.position = newV1Position; } } } public struct Triangle { … public void Rotate(Quaternion rotation, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(Vector3.zero, rotation, Vector3.one); var newV0Position = matrix.MultiplyPoint(V0.position - pivot) + pivot; var newV1Position = matrix.MultiplyPoint(V1.position - pivot) + pivot; var newV2Position = matrix.MultiplyPoint(V2.position - pivot) + pivot; if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } Edges[0].v0.normal = matrix.MultiplyPoint(V0.normal); Edges[1].v0.normal = matrix.MultiplyPoint(V1.normal); Edges[2].v0.normal = matrix.MultiplyPoint(V2.normal); } public void Scale(Vector3 scale, bool withCoincident = false) { var pivot = (V0.position + V1.position + V2.position) / 3; var matrix = Matrix4x4.TRS(pivot, Quaternion.identity, scale); var newV0Position = matrix.MultiplyPoint(V0.position - pivot); var newV1Position = matrix.MultiplyPoint(V1.position - pivot); var newV2Position = matrix.MultiplyPoint(V2.position - pivot); if (withCoincident) { var vertices = CustomMeshPool.GetMesh(_meshId).vertices; var maskV0 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V0.position); var maskV1 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V1.position); var maskV2 = CustomMeshPool.GetMesh(_meshId).GetVerticesInPosition(V2.position); for (int i = 0; i < vertices.Length; i++) { if (maskV0[i]) vertices[i] = newV0Position; else if (maskV1[i]) vertices[i] = newV1Position; else if (maskV2[i]) vertices[i] = newV2Position; } } else { Edges[0].v0.position = newV0Position; Edges[1].v0.position = newV1Position; Edges[2].v0.position = newV2Position; } } }
Swarm un trou soigné pour nous-mêmes
Dans la modélisation 3D, une opération d'extrusion est souvent utilisée. Pour sa mise en œuvre, le vecteur mouvement (déplacement) et l'ensemble des polygones doivent être connus. Le processus d'extrusion peut être décomposé en deux étapes:
1. Le décalage des polygones par un vecteur de mouvement donné (
décalage ). Dans ce cas, il faut dupliquer les sommets séparés par des polygones frontières pour ne pas perturber la position des éléments qui n'appartiennent pas à la partie déplacée. En d'autres termes, vous devez déchirer et déplacer la pièce sélectionnée. Si cette étape est terminée en premier, le modèle tombera probablement en morceaux qui devront être joints à l'avenir.
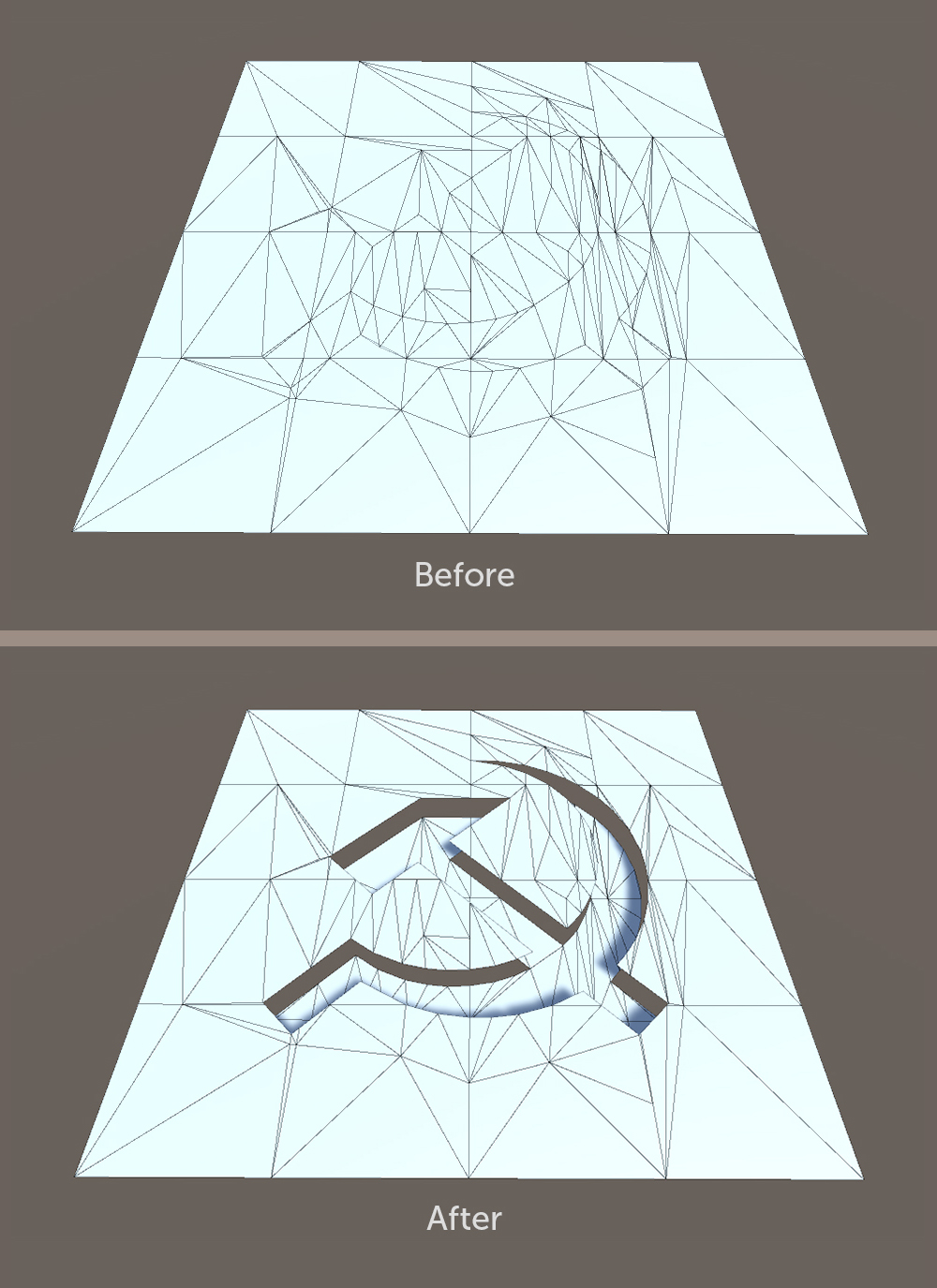
2. Ajout d'une nouvelle géométrie entre la frontière de la pièce déplacée et la frontière qui a été formée pendant l'extrusion. L'écart entre les parties principale et décalée du modèle est rempli de polygones formant un mur.
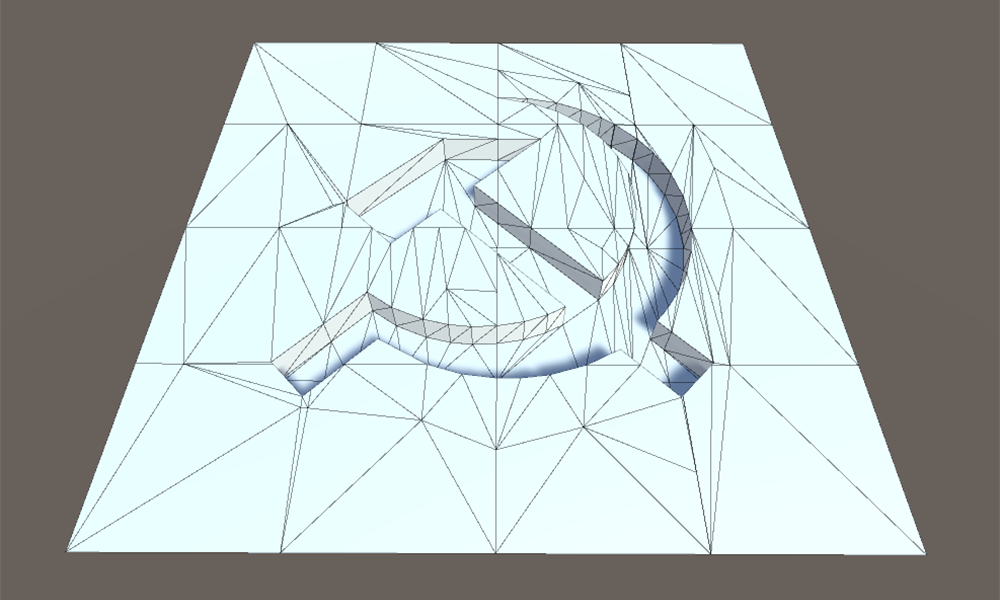
Dans la mise en œuvre, il est plus pratique de construire d'abord le mur, car avant le décalage, nous avons la position initiale des bords sur la bordure et nous pouvons utiliser ces données immédiatement. Sinon, vous devrez soit inverser la direction du vecteur de cisaillement, soit enregistrer certaines informations sur l'état initial du maillage.
Le modèle et ses parties avec lesquelles nous travaillons sont constitués d'ensembles de polygones adjacents par paires (triangles). Nous appelons chacun de ces ensembles un
cluster .
Deux clusters dédiés dans Blender
Tout d'abord, nous devons obtenir tous les bords des contours qui délimitent les clusters sélectionnés. Pour ce faire, ajoutez simplement les bords à la liste de manière séquentielle. Si un bord correspondant est trouvé, il doit être supprimé sans ajouter le bord actuel. Pour le bon fonctionnement d'un tel algorithme, il est nécessaire d'introduire une restriction: sur l'ensemble de triangles sélectionné il n'y a pas plus de deux arêtes coïncidentes. Dans les cas où l'
extrusion est utilisée, les modèles remplissent souvent cette condition, et un algorithme plus complexe nécessite de grandes ressources de calcul.
Liste des méthodes pour obtenir des bords appartenant aux contours internal static class LinkedListExtension { internal static IEnumerable<LinkedListNode<T>> Nodes<T>(this LinkedList<T> list) { for (var node = list.First; node != null; node = node.Next) { yield return node; } } } public struct Vertex { … public bool IsInPosition(Vector3 other) { return Mathf.Abs(position.x - other.x) < Mathf.Epsilon && Mathf.Abs(position.y - other.y) < Mathf.Epsilon && Mathf.Abs(position.z - other.z) < Mathf.Epsilon; } } public struct Edge { … public bool Coincides(Edge other, bool includeDirection = false) { return v0.IsInPosition(other.v0.position) && v1.IsInPosition(other.v1.position) || !includeDirection && v1.IsInPosition(other.v0.position) && v0.IsInPosition(other.v1.position); } } public class CustomMesh { … private LinkedList<Edge> ObtainHullEdges(int[] triIndices) { var edges = new LinkedList<Edge>(); for (var i = 0; i < triIndices.Length; i++) { var edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[0])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[0]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[1])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[1]); edge = edges.Nodes().FirstOrDefault(e => e.Value.Coincides(Triangles[triIndices[i]].Edges[2])); if (edge != null) edges.Remove(edge); else edges.AddFirst(Triangles[triIndices[i]].Edges[2]); } return edges; } }
Après avoir reçu tous les bords du contour, vous devez construire les murs correspondants. Il existe de nombreuses options de mise en œuvre, mais nous avons décidé de prendre le chemin de moindre résistance - générer des parallélogrammes dans la direction du vecteur de mouvement en fonction des bords séparément. Puisque nous avons tous un déplacement, à la suite de cette action, les parallélogrammes formeront une paroi solide et fermée pour chaque groupe. Reste à déterminer l'orientation des éléments du mur.
Le mur, comme tout le maillage, est constitué de triangles.
Selon la convention OpenGL , un triangle détaché est rendu à l'écran si, lors de la projection de ses points sur le plan de l'écran, les contourner dans l'ordre correspond à une marche dans le sens horaire:
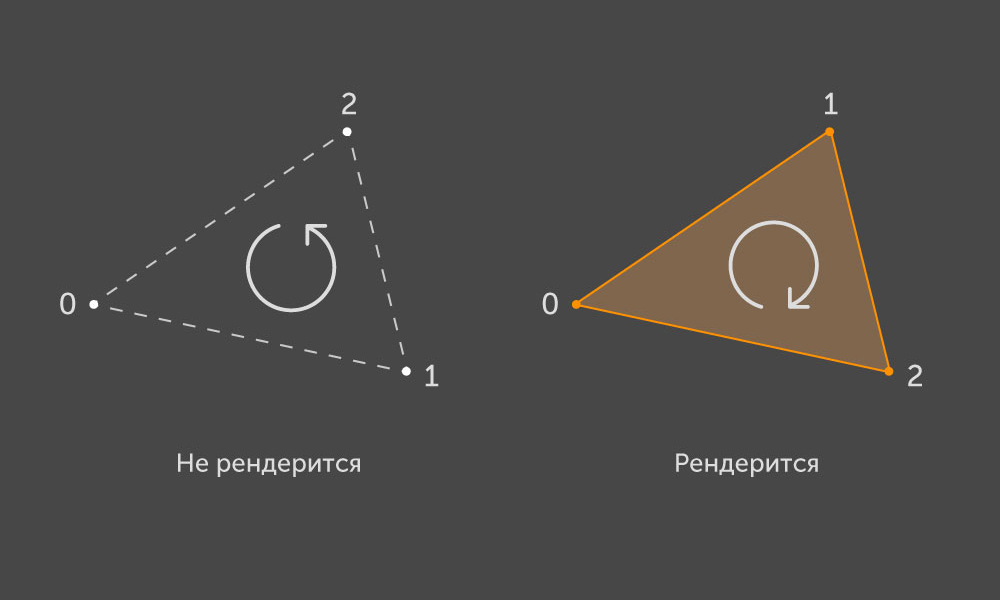
Ainsi, un triangle correspond à un certain vecteur normal qui définit la face avant. Chaque triangle est délimité par un contour convexe composé de trois arêtes. Chaque arête a deux sommets représentés dans notre structure comme
v0 et
v1 . Nous définissons la direction du bord de sorte que
v0 soit le début,
v1 soit la fin. Maintenant, si la direction des bords du triangle est définie en fonction du contournement de ses sommets, alors tout contour externe du cluster doit avoir un contournement dans le sens horaire ou antihoraire et tout contour interne - vice versa. Nous avons implémenté les constructeurs
CustomMesh et
Triangle afin que la traversée des sommets de tous les triangles corresponde à la direction horaire.
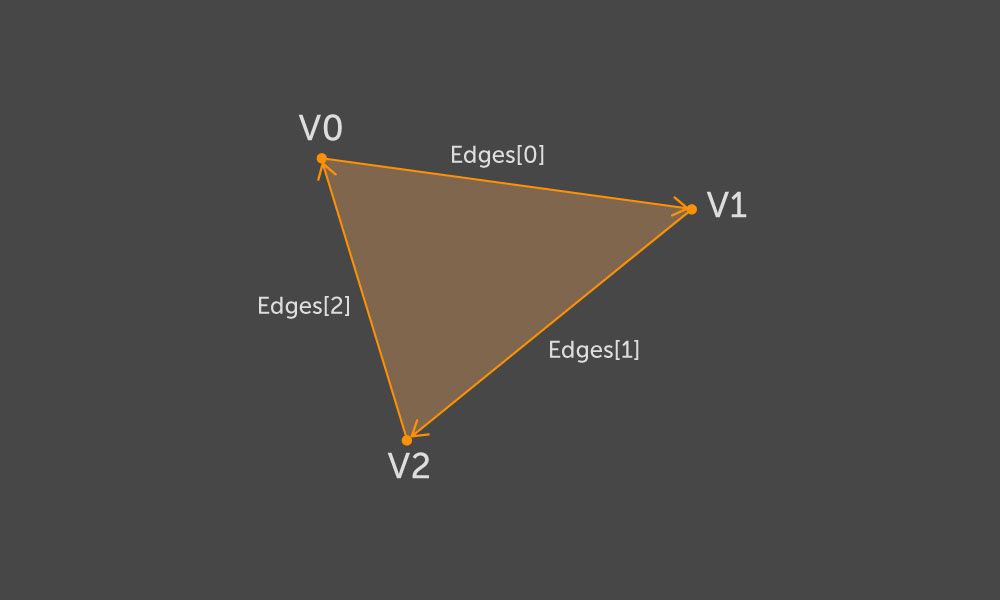
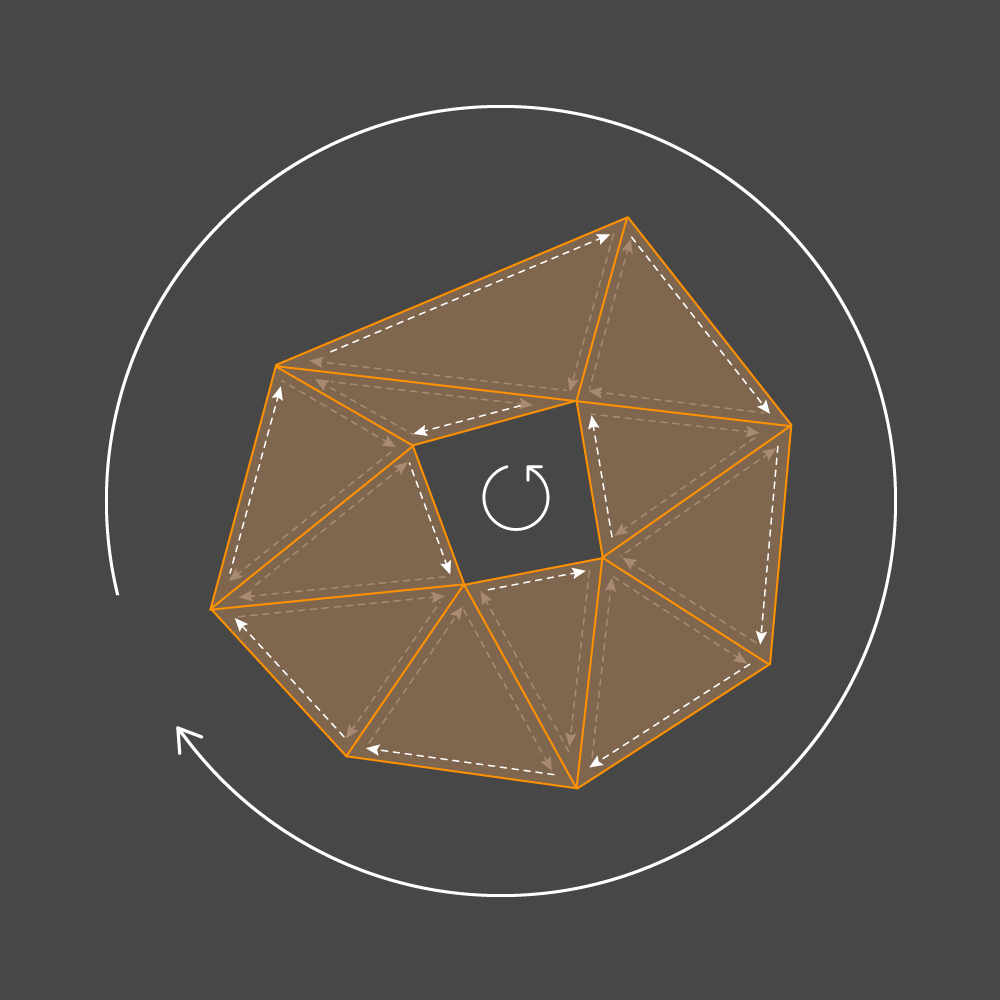
Ayant la direction de contourner le contour, nous pouvons dire avec certitude quel côté de la nervure est la partie intérieure du contour et lequel est l'extérieur. Sur la base de ces informations, nous choisirons l'orientation du mur. Soit (
v0, v1 ) l'arête sur la base de laquelle le parallélogramme souhaité doit être généré. Nous prenons les deux points
v2 et
v3 comme positions de décalage
v0 et
v1 . Ensuite, nous construisons deux triangles selon le schéma suivant:
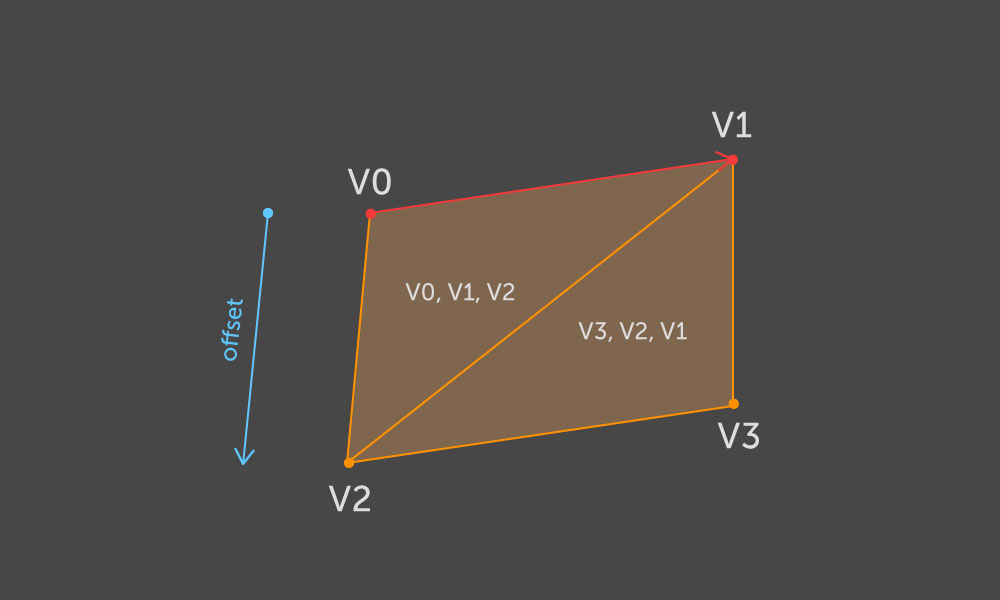
Et donc pour chaque bord du contour.
Liste d'une méthode de construction de murs à l'aide d'une liste d'arêtes public class CustomMesh { … private void ExtrudeEdgesSet(Edge[] edges, Vector3 offset) { if (offset == Vector3.zero || edges == null || edges.Length == 0) return; var initVerticesLength = vertices.Length; Array.Resize(ref vertices, initVerticesLength + edges.Length * 4); if (normals != null && normals.Length == initVerticesLength) { Array.Resize(ref normals, vertices.Length); } if (uv0 != null && uv0.Length == initVerticesLength) { Array.Resize(ref uv0, vertices.Length); } if (uv2 != null && uv2.Length == initVerticesLength) { Array.Resize(ref uv2, vertices.Length); } if (colors != null && colors.Length == initVerticesLength) { Array.Resize(ref colors, vertices.Length); } var initTrianglesLength = Triangles.Length; Array.Resize(ref Triangles, initTrianglesLength + edges.Length * 2); edges .AsParallel() .Select((edge, i) => { int j = initVerticesLength + i * 4; vertices[j] = edge.v0.position; vertices[j + 1] = edge.v1.position; vertices[j + 2] = edge.v0.position + offset; vertices[j + 3] = edge.v1.position + offset; if (normals != null && normals.Length == vertices.Length) { var normal = Vector3.Cross(vertices[j + 1] - vertices[j], offset); normals[j] = normals[j + 1] = normals[j + 2] = normals[j + 3] = normal; } if (uv0 != null && uv0.Length == vertices.Length) { uv0[j] = uv0[j + 2] = edge.v0.uv0; uv0[j + 1] = uv0[j + 3] = edge.v1.uv0; } if (uv2 != null && uv2.Length == vertices.Length) { uv2[j] = uv2[j + 2] = edge.v0.uv2; uv2[j + 1] = uv2[j + 3] = edge.v1.uv2; } if (colors != null && colors.Length == vertices.Length) { colors[j] = colors[j + 2] = edge.v0.color; colors[j + 1] = colors[j + 3] = edge.v1.color; } Triangles[initTrianglesLength + i * 2] = new Triangle( initTrianglesLength + i * 2, Id, j, j + 1, j + 2 ); Triangles[initTrianglesLength + i * 2 + 1] = new Triangle( initTrianglesLength + i * 2 + 1, Id, j + 3, j + 2, j + 1 ); return true; }).ToArray(); } }
Avec cette approche, la face avant des murs générés sera correcte pour les toboggans et les fosses. Il n'y a qu'une seule limitation importante: l'ensemble des triangles sur lesquels l'opération d'
extrusion est effectuée ne doit pas être enroulé autour de lui-même par rapport au vecteur de mouvement.
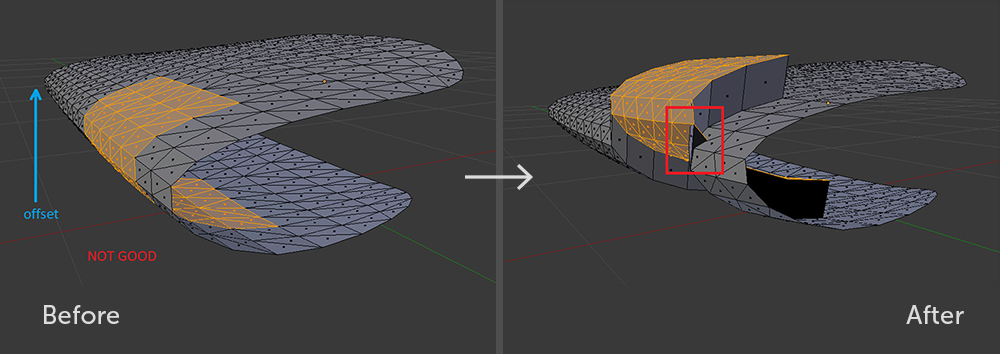Un sous-ensemble de polygones qui n'est pas valide en ce qui concerne le décalage. Même dans Blender avec une telle extrusion, il ne sera pas possible d'éviter une courbe géométrique.
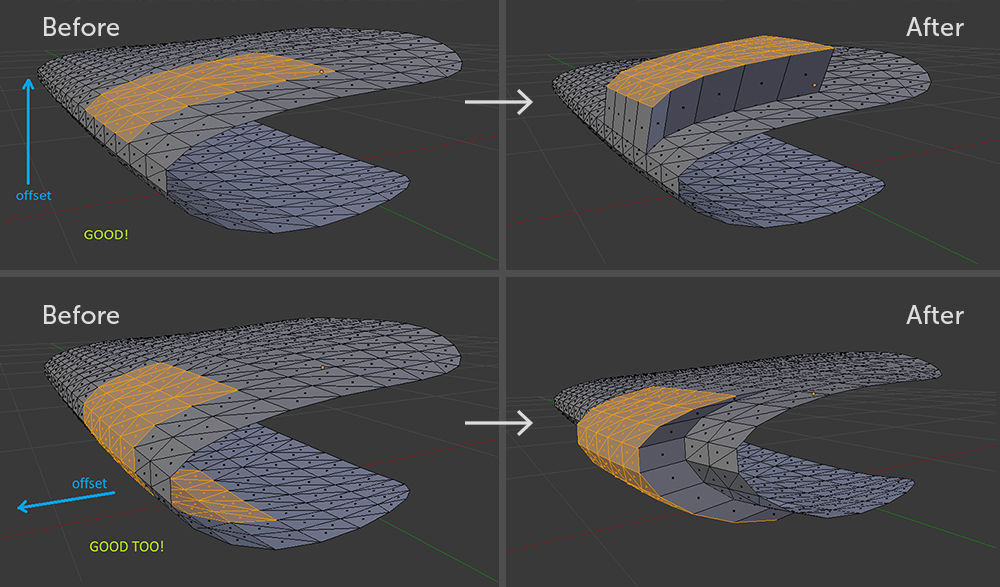Sous-ensembles valides de polygonesLe mur est prêt, il reste à décaler les triangles. Cette étape de l'algorithme est facile à comprendre, même si la mise en œuvre s'est avérée lourde.
Dans notre cas, nous devons nous assurer que chaque sommet du cluster n'appartient qu'à ses triangles. Si la condition n'est pas remplie, certains polygones voisins peuvent atteindre le cluster. La solution à cette situation consiste à dupliquer chaque sommet qui appartient à la fois à la grappe et au reste du modèle. Ensuite, pour tous les polygones du cluster, remplacez l'index de ce sommet par l'index en double. Lorsque la condition est satisfaite, nous déplaçons tous les sommets du cluster vers le vecteur de mouvement.
Liste d'une méthode pour déplacer un cluster de polygones public class CustomMesh { … private void TranslateTrianglesHard(int[] triIndices, Vector3 offset, int[] hullVerts) { var newVertexIndices = new Dictionary<int, int>(); var initVerticesCount = vertices.Length; Triangles.Where((t, i) => !triIndices.Contains(i)).Select(t => { if (hullVerts.Contains(t.V0.Index) && !newVertexIndices.ContainsKey(t.V0.Index)) newVertexIndices.Add(t.V0.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V1.Index) && !newVertexIndices.ContainsKey(t.V1.Index)) newVertexIndices.Add(t.V1.Index, initVerticesCount + newVertexIndices.Count); if (hullVerts.Contains(t.V2.Index) && !newVertexIndices.ContainsKey(t.V2.Index)) newVertexIndices.Add(t.V2.Index, initVerticesCount + newVertexIndices.Count); return false; }).ToArray(); Array.Resize(ref vertices, initVerticesCount + newVertexIndices.Count); foreach (var pair in newVertexIndices) vertices[pair.Value] = vertices[pair.Key] + offset; if (normals != null && normals.Length == initVerticesCount) { Array.Resize(ref normals, vertices.Length); foreach (var pair in newVertexIndices) normals[pair.Value] = normals[pair.Key]; } if (uv0 != null && uv0.Length == initVerticesCount) { Array.Resize(ref uv0, vertices.Length); foreach (var pair in newVertexIndices) uv0[pair.Value] = uv0[pair.Key]; } if (uv2 != null && uv2.Length == initVerticesCount) { Array.Resize(ref uv2, vertices.Length); foreach (var pair in newVertexIndices) uv2[pair.Value] = uv2[pair.Key]; } if (colors != null && colors.Length == initVerticesCount) { Array.Resize(ref colors, vertices.Length); foreach (var pair in newVertexIndices) colors[pair.Value] = colors[pair.Key]; } var alreadyMoved = new HashSet<int>(); for (var i = 0; i < triIndices.Length; i++) { if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V0.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V0.Index]; Triangles[triIndices[i]].Edges[0].v0.Index = index; Triangles[triIndices[i]].Edges[2].v1.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V0.Index)) { vertices[Triangles[triIndices[i]].V0.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V0.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V1.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V1.Index]; Triangles[triIndices[i]].Edges[0].v1.Index = index; Triangles[triIndices[i]].Edges[1].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V1.Index)) { vertices[Triangles[triIndices[i]].V1.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V1.Index); } if (newVertexIndices.ContainsKey(Triangles[triIndices[i]].V2.Index)) { var index = newVertexIndices[Triangles[triIndices[i]].V2.Index]; Triangles[triIndices[i]].Edges[1].v1.Index = index; Triangles[triIndices[i]].Edges[2].v0.Index = index; } else if (!alreadyMoved.Contains(Triangles[triIndices[i]].V2.Index)) { vertices[Triangles[triIndices[i]].V2.Index] += offset; alreadyMoved.Add(Triangles[triIndices[i]].V2.Index); } } } }
C'est fait. Maintenant, en additionnant les résultats de toutes les étapes, nous obtenons un trou ou une colline.
Liste de la méthode finale pour l'opération d'extrusion public class CustomMesh { … public void ExtrudeTriangles(int[] triIndices, Vector3 offset) { var edges = ObtainHullEdges(triIndices); ExtrudeEdgesSet(edges.ToArray(), offset); var hullVertices = edges.Select(edge => edge.v0.Index).ToArray(); TranslateTrianglesHard(triIndices, offset, hullVertices); } }
Après avoir joué avec les coordonnées du scan de texture et le déplacement des points de contour, vous pouvez obtenir un tel retrait:
Et ce n'est pas tout
En plus des opérations d'édition décrites ci-dessus, nous utilisons également d'autres méthodes pratiques pour travailler avec des modèles.
Par exemple, nous avons également écrit la méthode
Combine () pour combiner deux
CustomMesh . La principale différence entre notre implémentation et
UnityEngine.Mesh.CombineMeshes () est que si certains sommets sont complètement équivalents lors de la combinaison des maillages, nous n'en laissons qu'un, évitant ainsi une géométrie inutile.
Dans le même module, nous avons implémenté
l'algorithme de triangulation du plan de Delaunay . En l'utilisant, vous pouvez, par exemple, fermer un grand trou créé en utilisant
Extruder avec un couvercle plat avec une texture d'eau et obtenir un lac:
Eh bien, triez-le! Dans le prochain article, nous examinerons les caractéristiques de l'importation de
.fbx dans
Unity et les méthodes de validation de modèle dans un projet.
Pour une collation (juste pour lulz)