Le quatrième niveau du multi-univers de Max Tegmark

Il y a près de 10 ans, j'ai lu un article de Max Tegmark , un brillant physicien et philosophe, et y ai trouvé les réponses à de nombreuses questions qui m'ont tourmenté toute ma vie. L'article est étonnant, pendant deux mois j'en ai eu l'impression. Malheureusement, c'est Longrid, et aussi en anglais. Par conséquent, j'ai décidé de ne pas même la traduire - la traduction serait encore trop longue pour Habr, mais au moins exposer l'idée principale dans l'ordre qu'elle me semble logique, et en supprimant les détails inutiles (Max pardonne-moi!)

Formules et bagages

$$

$$A = bc$$

Qu'est ce que c'est Il est peu probable que cette formule vous dise quelque chose. Et si je l'écris comme ceci:

$$

$$F = ma$$

Ensuite, vous y reconnaîtrez immédiatement la loi de Newton. Bien sûr, les deux formules sont équivalentes, nous sommes juste habitués au fait que la force est notée F, masse m, de plus, nous voulons dire que la matière se déroule dans un espace tridimensionnel, que les corps ont des coordonnées, etc. Autrement dit, la théorie a deux composants: les formules et bla bla autour d'eux. Max appelle le bagage verbal du deuxième composant.

Considérez l'arbre des théories existantes:



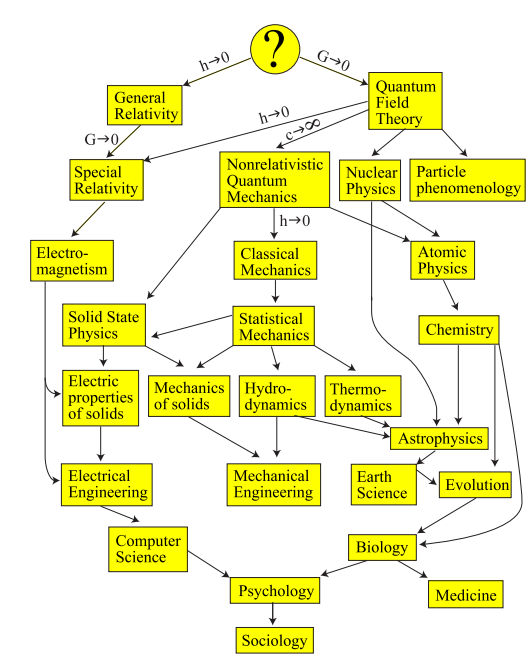
Tout en bas se trouve la sociologie, où il n'y a presque pas de formules, mais beaucoup de mots. En montant à l'étage, on rencontre des mathématiques de plus en plus compliquées. Mais avec les mots, la situation empire de plus en plus: essayez de savoir auprès d'un scientifique qui se consacre à la physique fondamentale l'heure qu'il est. Il est évident pour vous que le temps est une séquence d'événements et qu'il avance . Plus vous en savez et plus vous allez, moins cela devient évident. La description de ce qu'est le temps s'effondre de plus en plus au fait que le temps est la lettre t , qui est impliquée dans telle ou telle équation.

Alors Max remarque que:
À mesure que vous passez à un niveau de plus en plus fondamental, les mathématiques deviennent plus complexes et les bagages commencent à dégénérer de plus en plus. Dans la limite, suggère Max, la TOE (Théorie de tout - Théorie générale de tout) n'a pas de bagages . Ainsi, la TOE se compose uniquement de formules .

Ceci est le premier ingrédient. Souviens-toi de lui.

Physique «Au contraire»

Comment est-ce encore possible? La physique essaie de trouver des équations pour notre monde, basées sur des observations et des données expérimentales. Max suggère de regarder « Physique à partir de zéro », « Physique à partir de zéro », vous demandez l'équation, quel genre de monde obtenez-vous?

On peut fixer les lois du monde ... enfin, par exemple, le jeu "vie". Peut-on se passer d'une description verbale? Comment, par exemple, dire que l'espace des cellules est bidimensionnel? Grâce à des équations, en indiquant une loi de puissance, la vitesse à laquelle le nombre de cellules ne dépasse pas la distance N. Un autre exemple, les équations de la théorie des cordes ne convergent que si la dimension de l'espace est 10, 11 ou 26. Peut-être, au début, la formulation de la physique semblera difficile du point de vue axiomatique, mais les mathématiciens ont bien réussi créer des théories axiomatiques (et des mondes). Prenez, par exemple, les axiomatiques de Peano . Ce sont des formules pures, elles n'expliquent pas ce qu'est un «nombre», ce que cela signifie d'ajouter ou de multiplier.

Description vs équivalence.

Qu'avons-nous? Nous avons (allons) une TOE décrivant TOUT ce qui existe.
Une seconde ... Et que signifie «décrire»? Par exemple, la mécanique décrit le mouvement des corps. Mais nous savons que tout cela est possible grâce à un tas de simplifications: les corps ne sont pas des points matériels, il y a une résistance à l'air, des frottements, etc. Il existe des formules qui décrivent la réalité, mais nous savons que le monde réel est différent de l'idéal, décrit par des formules.

Mais dans le cas de la TOE, ce n'est pas le cas: aucun, absolument aucun aspect physique de la réalité n'est décrit par des formules - ou ce n'est pas la TOE. Quelle est la différence entre la théorie et la réalité dans ce cas, si elles sont absolument équivalentes?

Max fait valoir que dans le cas de la TOE, les mathématiques ne décrivent pas la réalité et les mathématiques sont la réalité . Si vous êtes soudainement en désaccord, l'inverse signifierait qu'il y a des équations avec leurs solutions, il y a exactement le même monde qui est complètement soumis aux formules indiquées, mais aussi réel . Dans ce cas, les mots « toujours réel » sont des bagages verbaux dans leur forme pure, que nous avons abandonnés ci-dessus, une telle anima sola moderne de la physique. Ainsi, nous sommes obligés d'admettre qu'au niveau fondamental, la physique et les mathématiques sont une seule et même chose.

Formules et flammes

Max n'était pas le premier à avoir de telles idées. Hawking lui-même a posé la question: " Mais qu'est-ce que la flamme respire exactement dans ces équations, créant l'univers?" " " Qu'est-ce qui insuffle du feu dans les équations et crée un univers à décrire? "



Si nous disions que notre univers est spécial parce qu'il existe , nous serions à nouveau renvoyés d'un pas en arrière vers le concept d'anima sola. Non, rien ne souffle la flamme dans nos formules. Il serait étrange que tous les systèmes axiomatiques de mathématiques soient divisés en deux classes inégales: les systèmes pour lesquels il existe des univers et les systèmes malchanceux. Cela contredit toute l'hypothèse de l'univers mathématique.

Tout cela ne peut s'expliquer que de cette façon: s'il n'y a pas d'anima sola, alors tous les systèmes axiomatiques sont égaux et l'univers correspond à chaque système axiomatique. Oui, la plupart des systèmes sont très probablement triviaux, et peut-être que la plupart des axiomatiques ne donnent pas la possibilité de développer (c'est-à-dire d'apparaître dans des solutions) des systèmes complexes et non triviaux et, en particulier, la vie.

«La physique vice versa» attend toujours ses futurs chercheurs. Je donnerais cher pour savoir si notre univers est le plus simple de ceux où la vie intelligente est possible ou non.

Réponses à quelques questions

Fait intéressant, après la première étape (TOU n'a pas de bagages), la deuxième étape (les mathématiques et la physique sont une seule et même chose) et la troisième étape (chaque axiomatique crée un univers) ont été forcées. Voilà jusqu'où nous sommes arrivés.

Et pourquoi l'univers existe-t-il même?
Réponse: car il peut exister.

Quand ces structures sont-elles apparues et pourquoi sont-elles apparues?

Les structures mathématiques n'existent pas dans le temps et l'espace. Ils existent simplement.

Sommes-nous une émulation?

Non. Pour l'existence de structures mathématiques, aucune machine n'est nécessaire pour les «compter». Le nombre 19 est simple, qu'il y ait ou non un ordinateur qui essaie tout le temps de le diviser en un cycle, en vérifiant la simplicité

Et est-ce généralement comme de la science ou des fantasmes?

Comment postuler quelque chose que nous ne pouvons pas vérifier fondamentalement? Max attend cette critique. En fait, ce n'est pas la première fois que nous faisons cela. Nous sommes habitués depuis longtemps au concept du multivers.



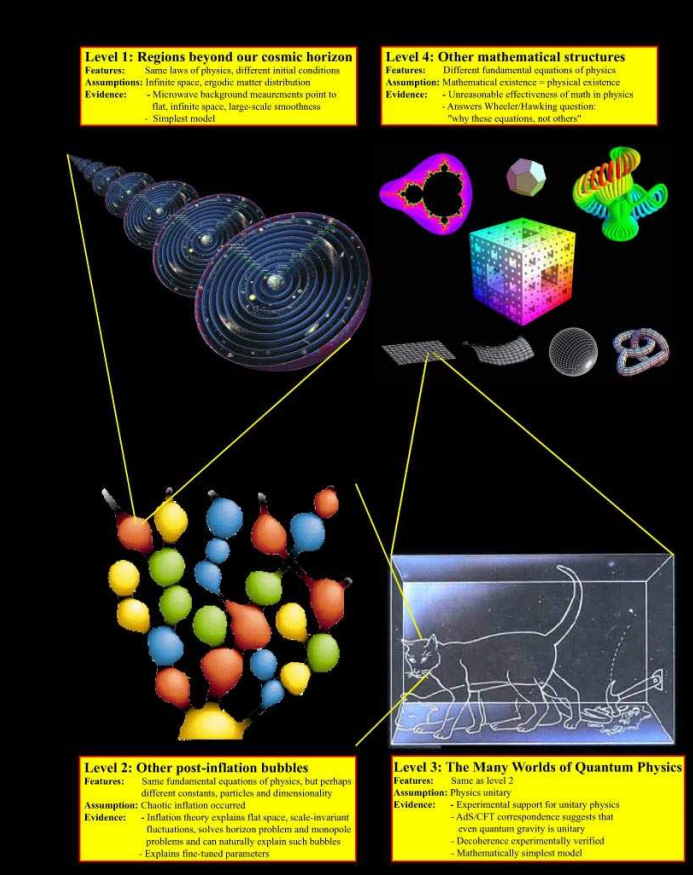Au niveau 1, nous parlons de zones de l'univers qui s'éloignent si rapidement de nous en raison de l'expansion qu'elles ne seront plus jamais liées de manière causale avec nous. Néanmoins, pas un seul cosmologiste ne tournera la langue pour dire qu'il n'y a rien là-bas, car on ne peut pas y voler.

Au niveau 2, nous parlons d'autres «bulles» dans la théorie de l' inflation éternelle, où, peut-être, sous les mêmes lois de la physique, d'autres conditions initiales et d'autres constantes physiques

Le niveau 3 est formé par les univers alternatifs du Multivers interprétés par Everett . Ce sera un article séparé.



Nous sommes obligés d'accepter l'existence du niveau 4 , correspondant à d'autres univers mathématiques que nous n'avons pas encore étudiés (théoriquement).