Développer un hexapode à partir de zéro (partie 4) - trajectoires et séquences mathématiques

Bonjour à tous! Le développement des hexapodes est allé encore plus loin. Cette fois, les trajectoires du mouvement des membres sont mises en œuvre et testées - la prochaine partie des mathématiques du mouvement. Dans cet article, je parlerai de ces trajectoires et séquences de base pour le mouvement. J'espère que ce sera intéressant.

Stades de développement:
Partie 1 - Conception
Partie 2 - Assemblage
Partie 3 - Cinématique
Partie 4 - Trajectoires et séquences mathématiques
Partie 5 - Électronique
Partie 6 - transition vers l'impression 3D
Partie 7 - Nouveaux logements, logiciels d'application et protocoles de communication

Trajectoires

L'essence de ce mécanisme est que lorsque vous définissez deux points, vous pouvez choisir la trajectoire du membre. En se déplaçant d'un point à un autre, les coordonnées changeront selon certaines équations paramétriques. Le mécanisme s'est avéré assez puissant et vous permet d'obtenir des courbes de mouvement intéressantes. Il implémente également le lissage des mouvements en modifiant le pas du paramètre t - plus le pas est petit, plus il y aura de points intermédiaires, plus la vitesse est faible et la fluidité du mouvement plus élevée.

La procédure de réglage des paramètres de la trajectoire à certains endroits est un peu incompréhensible et vous pouvez vous y embrouiller. La difficulté réside dans le fait que lors de la définition des coordonnées des points de départ et d'arrivée, les coordonnées des points réels dans l'espace ne sont pas toujours définies, c'est-à-dire certaines coordonnées définissent les paramètres de trajectoire. J'ai dû écrire un programme qui affiche un chemin donné et vérifie en même temps l'accessibilité de chaque point du chemin.

Le pilote prend en charge les trajectoires de mouvement suivantes:

1. XYZ_LINAR est la plus simple de toutes les trajectoires. La trajectoire est utilisée pour avancer, reculer, monter et descendre. Toutes les coordonnées changent linéairement et sont calculées comme suit:
   
   

   x = t * (x1 - x0) / 180.0f + x0; y = t * (y1 - y0) / 180.0f + y0; z = t * (z1 - z0) / 180.0f + z0; 

   
   Ici, nous comprenons qu'il n'y a aucun problème. Les coordonnées spécifient les angles parallélépipédiques et elles coïncident avec les coordonnées réelles. Le mouvement se produit le long de la diagonale de la boîte.
   
   
   Visualisation de la trajectoire

   
   
   
   
   
   
2. YZ_ARC_Y_LINEAR - cette trajectoire vous permet d'implémenter un mouvement le long d'un arc. La trajectoire est utilisée lors des virages lorsque vous devez déplacer un membre au sol. Les coordonnées sont calculées comme suit:
   
   

    float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // Circle Y y = t * (y1 - y0) / 180.0f + y0; z = R * cos(t_mapped_rad); // Circle X 

   
   C'est là que le plaisir commence. Les coordonnées spécifient la direction des rayons pour limiter l'arc et peuvent ne pas coïncider avec les coordonnées réelles. Les rayons sont dans le même plan, tandis que le rayon du cercle est égal à la longueur du vecteur jusqu'au point de départ.
   
   
   Visualisation de la trajectoire

   
   
   
   
   
   
3. XZ_ARC_Y_SINUS - cette trajectoire vous permet également d'implémenter un mouvement le long d'un arc, mais plus complexe que YZ_ARC_Y_LINEAR. La trajectoire est utilisée lors des virages, lorsque vous devez déplacer un membre dans les airs. Les coordonnées sont calculées comme suit:
   
   

    float R = sqrt(x0 * x0 + z0 * z0); float atan0 = RAD_TO_DEG(atan2(x0, z0)); float atan1 = RAD_TO_DEG(atan2(x1, z1)); float t_mapped_rad = DEG_TO_RAD(t * (atan1 - atan0) / 180.0f + atan0); x = R * sin(t_mapped_rad); // circle Y y = (y1 - y0) * sin(DEG_TO_RAD(t)) + y0; z = R * cos(t_mapped_rad); // circle X 

   
   Le plaisir continue. Les coordonnées spécifient également la direction des rayons pour limiter l'arc, mais elles ne coïncident PAS avec les coordonnées réelles. La coordonnée Y du point cible définit la hauteur du sinus.
   
   
   Visualisation de la trajectoire

   
   
   
   
4. XZ_ELLIPTICAL_Y_SINUS - cette trajectoire vous permet d'implémenter un mouvement le long d'une ellipse. La trajectoire est utilisée pour avancer et reculer, lorsque vous devez déplacer un membre dans les airs. Cette trajectoire est une complication de XZ_ARC_Y_SINUS et n'était nécessaire qu'en raison de la démarche visuellement laide lors de l'utilisation de XZ_ARC_Y_SINUS (jambes trop étendues). Les coordonnées sont calculées comme suit:
   
   

    float a = (z1 - z0) / 2.0f; float b = (x1 - x0); float c = (y1 - y0); x = b * sin(DEG_TO_RAD(180.0f - t)) + x0; // circle Y y = c * sin(DEG_TO_RAD(t)) + y0; z = a * cos(DEG_TO_RAD(180.0f - t)) + z0 + a; 

   
   Les coordonnées spécifient les angles parallélépipédiques et elles ne coïncident PAS avec les coordonnées réelles. Le mouvement se produit à partir des coins inférieurs de la boîte, situés dans le même plan que de toucher le haut de sa partie. Il vaut mieux regarder l'image dans le spoiler, je ne sais pas comment la décrire brièvement avec des mots.
   
   
   Visualisation de la trajectoire

   
   

Ceci complète les mathématiques de base du mouvement de l'hexapode. Dans mon projet, c'est un minimum nécessaire pour la mise en œuvre de presque tous les mouvements.

Les séquences

Un peu de théorie

Les séquences sont les actions élémentaires qui composent la démarche. Ils sont divisés en cycliques et non cycliques.

• Les séquences cycliques peuvent être répétées plusieurs fois et à la fin de chaque cycle, les membres doivent retrouver leur position d'origine (mouvement et rotation);
• Les séquences non cycliques ne sont effectuées qu'une seule fois (montée et descente);

Chaque séquence comporte trois blocs d'itération: bloc de préparation, bloc principal, bloc d'achèvement.

• Bloc d'entraînement - contient des itérations pour déplacer les membres à la position de départ de la séquence. Dans mon cas, aller de l'avant nécessite de mettre vos jambes dans une certaine position avant de commencer à bouger. Il est exécuté une fois lors de la transition vers la séquence;
• Bloc principal - contient l'itération principale de la séquence. Elle peut être effectuée de manière cyclique;
• Fin de bloc - contient des itérations pour déplacer les membres vers la position de base (la position dans laquelle les membres sont placés après le levage);

La figure ci-dessous montre la séquence pour avancer.

• Les points rouges indiquent la position initiale des membres avant de commencer à bouger
• Les lignes bleues indiquent les trajectoires du membre au sol
• Les lignes noires indiquent les trajectoires du membre dans l'air
• Les flèches indiquent la séquence

Les coordonnées des points sont sélectionnées en fonction de la configuration du boîtier. J'ai choisi les points le plus près possible du corps pour réduire la longueur du levier. Dans un cycle de la séquence, l'hexapode se déplace de 18 cm (en 1 cycle 2 pas sont effectués - 1 pas en 3 membres). Si vous augmentez la distance, les membres commenceront à s'accrocher les uns aux autres. Ce paramètre n'est limité que par la configuration du boîtier.


La séquence est définie par deux points (1, 2) pour chaque membre et deux chemins sont utilisés: XYZ_LINEAR (lignes bleues) et XZ_ELLIPTICAL_Y_SINUS (lignes noires). Le point 1 est utilisé par le chemin XZ_ELLIPTICAL_Y_SINUS pour définir la hauteur du sinus et, par conséquent, la hauteur à laquelle la jambe montera. Les points 2 et 3 sont de vrais points qu'un membre atteint en se déplaçant.

L'emplacement des points dépend uniquement de votre imagination et des capacités de l'hexapode. Peut-être que tout s'est révélé un peu compliqué et qu'il existe une option plus simple, mais apparemment je ne l'ai pas encore atteinte.

Implémentation

Voyons maintenant la mise en œuvre de tout ce bonheur. Les structures avec des paramètres de séquence sont les suivantes:

 typedef struct { point_3d_t point_list[SUPPORT_LIMB_COUNT]; path_type_t path_list[SUPPORT_LIMB_COUNT]; uint32_t smooth_point_count; } sequence_iteration_t; typedef struct { bool is_sequence_looped; uint32_t main_sequence_begin; uint32_t finalize_sequence_begin; uint32_t total_iteration_count; sequence_iteration_t iteration_list[15]; sequence_id_t available_sequences[SUPPORT_SEQUENCE_COUNT]; } sequence_info_t; 

sequence_iteration_t - contient des informations sur l'itération de la séquence:

• point_list - un tableau de points pour chaque membre au format XYZ;
• path_list - un tableau de trajectoires pour chaque membre;
• smooth_point_count - définit le nombre de points de chemin (étape de paramètre t);

sequence_info_t - contient des informations sur la séquence entière:

• is_sequence_looped - définit le type de séquence: cyclique ou non;
• main_sequence_begin - définit l'index de départ du bloc principal dans le tableau iteration_list;
• finalize_sequence_begin - définit l'index de départ du bloc d'achèvement dans le tableau iteration_list;
• total_iteration_count - définit le nombre d'itérations dans la séquence;
• iteration_list - un tableau d'itérations;
• available_sequences - définit la liste des séquences disponibles pour la transition de la séquence actuelle (par exemple, nous ne pouvons pas commencer à marcher sans nous lever d'abord du sol);

REMARQUE: L'index du bloc de préparation n'est pas intentionnellement indiqué; il est toujours situé au début du tableau d'itérations.

Malheureusement, je ne peux pas fournir de code pour déterminer la séquence ici, car il est assez large et a l'air terrible après les transferts. Je laisse juste un lien vers le fichier de définition ici.

Schéma de traitement des mouvements

Il vaut la peine de distinguer tous les cercles de l'enfer que la séquence traverse au moment de l'exécution. Le schéma de traitement est le suivant:

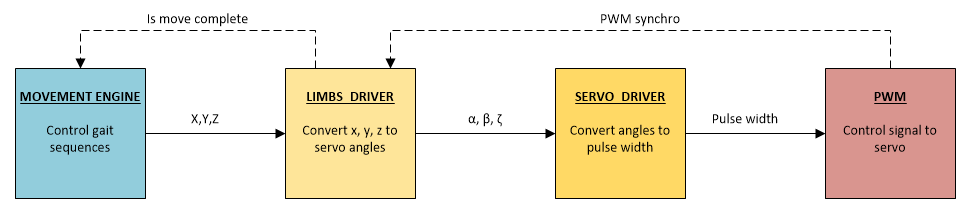
1. MOTEUR DE MOUVEMENT - organise le traitement et la commutation entre les séquences. Aucun calcul n'y est effectué. S'il est simplifié, ce module glisse le point suivant vers le module LIBMS DRIVER une fois le traitement en cours terminé.
   Entrée module: tableau de coordonnées des points cibles.
   Sortie du module: point cible pour l'itération actuelle de la séquence.
2. LIBMS DRIVER est le plus complexe de tous les modules. Toutes les mathématiques du mouvement y règnent: cinématique inverse, calculs de trajectoire et lissage des mouvements. Ce module a une synchronisation stricte avec le module PWM. Les calculs sont effectués avec une fréquence de 150 Hz, respectivement, l'impulsion de commande vers les entraînements est également fournie avec une fréquence de 150 Hz.
   Entrée module: coordonnées du point cible.
   Sortie module: angles de rotation servo.
3. SERVO DRIVER . Il n'y a rien de spécial, à part un tas de paramètres pour la configuration et le réglage des disques.
   Entrée module: angles de rotation servo.
   Sortie module: contrôle de la largeur d'impulsion.
4. PILOTE PWM . Logiciel pilote PWM pour le contrôle du lecteur. Ici, les broches se contractent juste au bon moment. La variable de synchronisation synchro PWM est incrémentée à chaque période PWM.
   Entrée module: contrôle de la largeur d'impulsion.
   Sortie du module: impulsions sur les broches de contrôle.

J'ai essayé de rendre les modules indépendants les uns des autres et j'ai réussi. Cela vous permet d'insérer dans ce circuit n'importe quel module intermédiaire (par exemple, le module d'adaptation au paysage) et rien ne se cassera en même temps, tandis que l'implémentation se produira avec des changements minimes dans le code.

Dernières nouvelles et projet d'écrevisses trouvées