Une légende urbaine raconte que le créateur de sachets de sucre, de bâtonnets, s'est pendu quand il a appris que les consommateurs ne les cassent pas en deux au-dessus d'une tasse, mais déchirent doucement la pointe. Ce n'est bien sûr pas le cas, mais si cette logique est suivie, alors un amateur de bière Guinness britannique du nom de William Gosset ne devrait pas simplement se pendre, mais par sa rotation dans le cercueil devrait déjà forer la Terre au centre même. Et tout cela parce que son invention emblématique, publiée sous le pseudonyme Student , a été utilisée de manière désastreuse pendant des décennies.
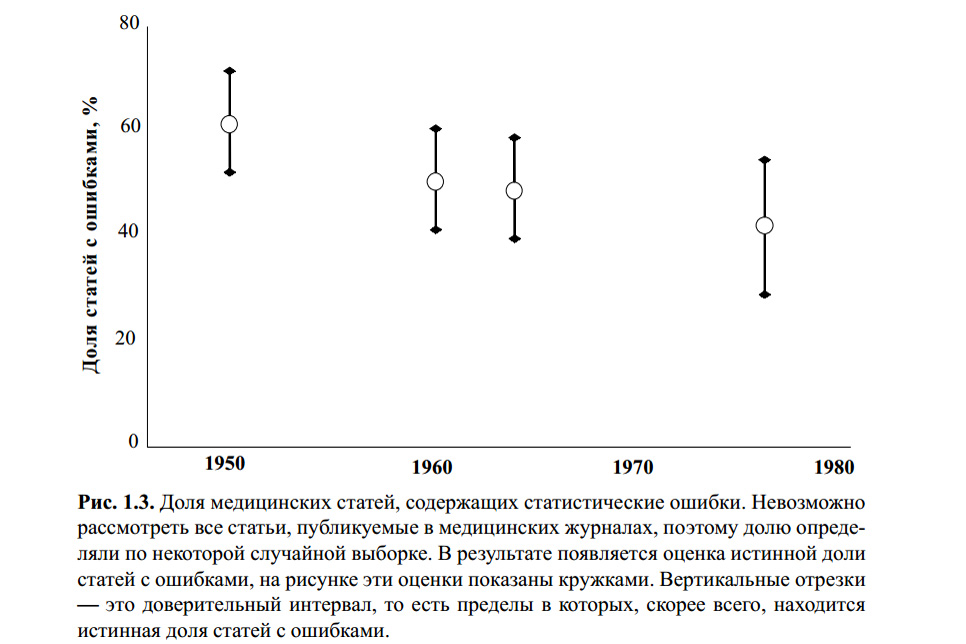
La figure ci-dessus est extraite du livre de S. Glanz. Statistiques biomédicales. Per. de l'anglais - M., Pratique, 1998 .-- 459 p. Je ne sais pas si quelqu'un a vérifié les erreurs statistiques dans les calculs de ce graphique. Cependant, un certain nombre d'articles modernes sur le sujet et ma propre expérience indiquent que le critère t de Student reste le plus célèbre, et donc le plus populaire, avec ou sans.
La raison en est une éducation superficielle (les enseignants stricts enseignent que vous devez "vérifier les statistiques", sinon uuuuuu!), La facilité d'utilisation (les tableaux et les calculatrices en ligne sont disponibles en abondance) et une réticence banale à se plonger dans le fait que "et ainsi cela fonctionne." La plupart des gens qui ont utilisé ce critère au moins une fois dans leur mémoire ou même dans leurs travaux scientifiques diront quelque chose comme: "Eh bien, nous avons comparé 5 écoliers en colère et 7 écoliers-joueurs en termes d'agression, notre valeur de tableau se rapproche de p = 0,05 et cela signifie que les jeux sont mauvais. Eh bien, oui, pas exactement, mais avec une probabilité de 95%. " Combien d'erreurs logiques et méthodologiques ont-ils commises?
Les bases
Sur quoi le test t des élèves est-il basé? La logique est tirée du théorème bayésien, la base mathématique est de la distribution gaussienne, la méthodologie est basée sur l'analyse de la variance:

où le paramètre μ est l'espérance mathématique (valeur moyenne) de la distribution et le paramètre σ est l'écart type (σ ² est la variance) de la distribution.
Qu'est-ce que l'analyse de la variance? Imaginez un public Habr, trié par le nombre de personnes de chacun d'un certain âge. Le nombre de personnes par âge est susceptible d'obéir à la distribution normale - selon la fonction de Gauss:
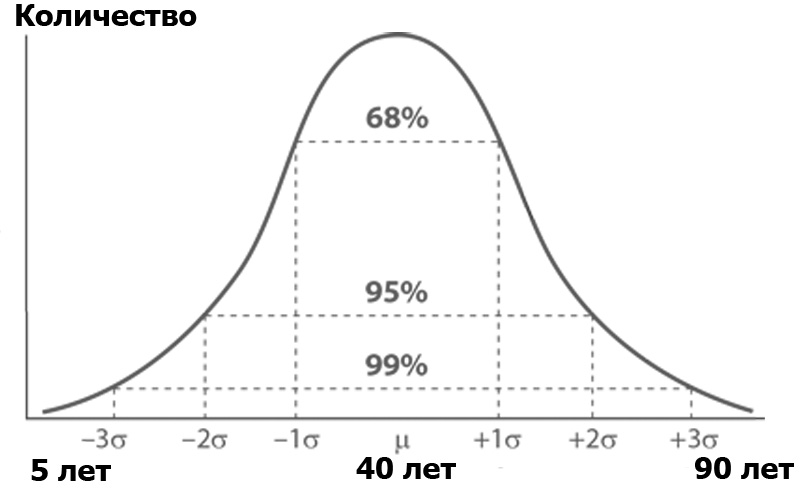
La distribution normale a une propriété intéressante - presque toutes ses valeurs se situent dans la limite de trois écarts-types de la valeur moyenne. Et quel est l'écart type? C'est la racine de la variance. La dispersion , à son tour, est la somme des carrés de la différence de tous les membres de la population générale et de la valeur moyenne divisée par le nombre de ces membres:
C'est-à-dire que chaque valeur a été soustraite de la moyenne, au carré pour tuer les inconvénients, puis a pris la moyenne, stupidement résumée et divisée par le nombre de ces valeurs. Le résultat est une mesure de la dispersion moyenne des valeurs par rapport à la variance moyenne.
Imaginez que nous avons sélectionné deux échantillons dans cette population générale : les lecteurs du hub Cryptocurrency et les lecteurs du hub Old Iron. En faisant un échantillon aléatoire , nous obtenons toujours des distributions proches de la normale . Et maintenant, nous avons un petit distributeur au sein de notre population:
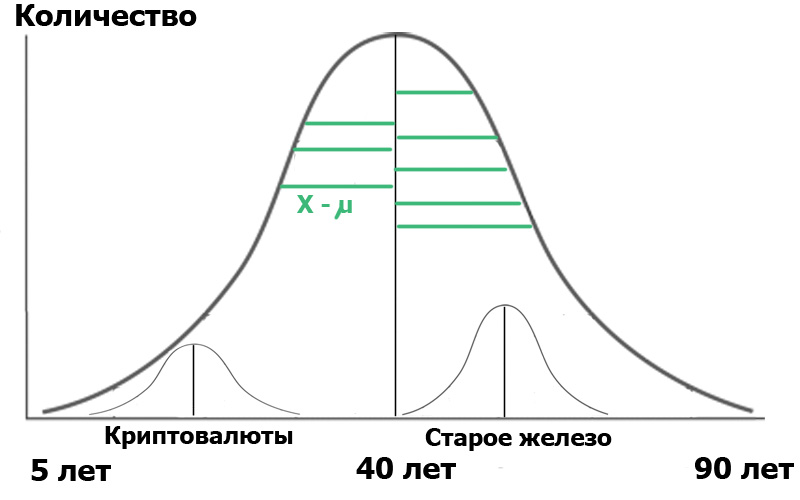
Pour plus de clarté, j'ai montré des segments verts - la distance entre les points de distribution et la valeur moyenne. Si les longueurs de ces segments verts sont au carré, additionnées et moyennées - ce sera la variance.
Et maintenant - attention. Nous pouvons caractériser la population à travers ces deux petits échantillons. D'une part, les variances des échantillons caractérisent la variance de l'ensemble de la population. En revanche, les valeurs moyennes des échantillons eux-mêmes sont également des nombres pour lesquels la variance peut être calculée! Donc: nous avons la moyenne des variances des échantillons et la variance des valeurs moyennes des échantillons.
Ensuite, nous pouvons effectuer une analyse de la variance, la représentant approximativement sous la forme d'une formule logique:
Que nous donnera la formule ci-dessus? Très simple. En statistique, tout commence par «l'hypothèse nulle», qui peut être formulée comme «il nous a semblé», «toutes les coïncidences sont aléatoires» - dans le sens, et «il n'y a pas de lien entre les deux événements observés» - si strictement. Ainsi, dans notre cas, l'hypothèse nulle serait l'absence de différences significatives entre la répartition par âge de nos utilisateurs dans deux hubs. Dans le cas de l'hypothèse nulle, notre diagramme ressemblera à ceci:
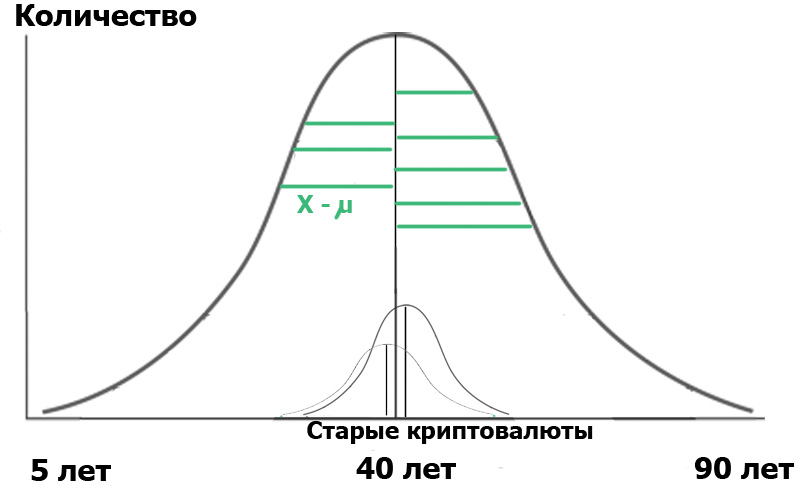
Cela signifie que les variances des échantillons et leurs valeurs moyennes sont très proches ou égales les unes aux autres, et donc, d'une manière très générale, notre critère
Mais si les variances des échantillons sont égales, mais que les âges des habrauseurs sont vraiment très différents, alors le numérateur (variance des valeurs moyennes) sera grand, et F sera beaucoup plus que l'unité. Le diagramme ressemblera alors davantage à la figure précédente. Et que nous apportera-t-il? Rien, si vous ne faites pas attention au libellé: l'hypothèse nulle serait l'absence de différences significatives .
Mais la signification ... nous l'avons définie nous-mêmes. Il est noté α et a la signification suivante: le niveau de signification est la probabilité maximale acceptable de rejeter par erreur l'hypothèse nulle . En d'autres termes, nous considérerons notre événement comme une différence significative entre un groupe et un autre, uniquement si la probabilité P de notre erreur est inférieure à α. C'est le p <0,05 notoire, car généralement dans la recherche biomédicale, le niveau de signification est fixé à 5%.
Eh bien, alors tout est simple. En fonction de α, il existe des valeurs critiques de F, à partir desquelles nous rejetons l'hypothèse nulle. Ils sont délivrés sous forme de tableaux, que nous sommes habitués à utiliser. C'est pour l'analyse de la variance. Et l'étudiant?
Ainsi a dit l'étudiant
Et le critère de l'étudiant n'est qu'un cas particulier d'analyse de variance. Encore une fois, je ne vais pas vous surcharger avec des formules qui sont facilement google, mais je vais transmettre l'essentiel:
Donc, toute cette longue explication devait être très grossière et fluide, mais montrer clairement sur quoi le critère t est basé. Et en conséquence, de quelles propriétés inhérentes découlent directement les limites de son utilisation, sur lesquelles même les scientifiques professionnels font souvent des erreurs.
Première propriété: Normalité de la distribution.
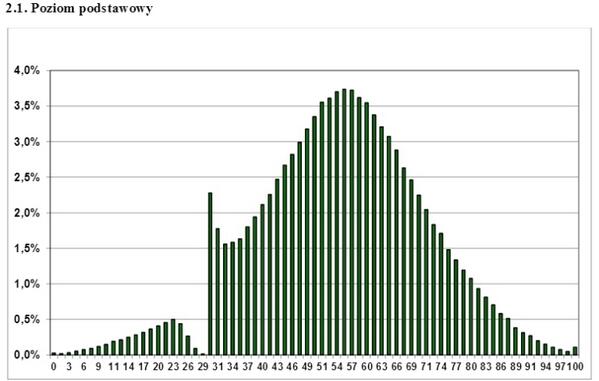
Il s'agit d'un graphique de la répartition des résultats des examens de l'État polonais sur Internet sur quelques années. Quelle conclusion peut-on en tirer? Que cet examen n'est pas réussi seulement complètement repoussé Gopnik? Quels enseignants «atteignent» les élèves? Non, un seul - à une distribution autre que la normale, vous ne pouvez pas appliquer des critères d'analyse paramétrique, tels que Student. Si vous avez un tableau de distribution unilatéral, dentelé, ondulé, discret - oubliez le critère t, vous ne pouvez pas l'utiliser. Cependant, cela est parfois ignoré avec succès, même par de sérieux travaux scientifiques.
Que faire dans ce cas? Utilisez les critères d'analyse non paramétriques. Ils mettent en œuvre une approche différente, à savoir le classement des données, c'est-à-dire le passage des valeurs de chacun des points au rang qui lui est attribué. Ces critères sont moins précis que ceux paramétriques, mais au moins leur utilisation est correcte, contrairement à l'utilisation injustifiée du critère paramétrique sur une population anormale. Parmi ces critères, le critère U de Mann-Whitney est le plus connu, et il est souvent utilisé comme critère "pour un petit échantillon". Oui, il vous permet de traiter des échantillons jusqu'à 5 points, mais cela, comme cela doit déjà être clair, n'est pas son objectif principal.
La deuxième propriété: vous souvenez-vous de la formule? Les valeurs du critère F ont changé avec la différence (variance accrue) des valeurs moyennes des échantillons . Mais le dénominateur, c'est-à-dire les écarts eux-mêmes, ne devrait pas changer. Par conséquent, un autre critère d'applicabilité devrait être l'égalité des variances. Le fait que ce contrôle soit encore moins observé est dit, par exemple, ici: Erreurs dans l'analyse statistique des données biomédicales. Leonov V.P. Journal international de pratique médicale, 2007, no. 2, p . 19-35 .
Propriété trois: comparaison de deux échantillons. Ils aiment utiliser le critère t pour comparer plus de deux groupes. En règle générale, cela se fait comme suit: les différences entre le groupe A de B, B de C et A de C. sont comparées par paires, puis, sur cette base, une certaine conclusion est tirée, ce qui est absolument incorrect. Dans ce cas, l'effet de comparaisons multiples se produit.
Ayant obtenu une valeur suffisamment élevée de t dans l'une des trois comparaisons, les chercheurs rapportent que «P <0,05». Mais en fait, la probabilité d'erreur dépasse largement 5%.
Pourquoi?
Nous le comprenons: par exemple, l'étude a adopté un niveau de signification de 5%. Cela signifie que la probabilité maximale acceptable de rejeter par erreur l'hypothèse nulle lors de la comparaison des groupes A et B est de 5%. Il semblerait que tout soit correct? Mais la même erreur exacte se produira dans le cas de la comparaison des groupes B et C, et lors de la comparaison des groupes A et C également. Par conséquent, la probabilité d'une erreur dans son ensemble avec ce type d'évaluation ne sera pas de 5%, mais bien plus. En général, cette probabilité est égale à
P ′ = 1 - (1 - 0,05) ^ k
où k est le nombre de comparaisons.
Ensuite, dans notre étude, la probabilité de se tromper en rejetant l'hypothèse nulle est d'environ 15%. Lorsque l'on compare les quatre groupes, le nombre de paires et, par conséquent, les comparaisons possibles par paires est de 6. Par conséquent, avec un niveau de signification dans chacune des comparaisons de 0,05
la probabilité de détecter par erreur une différence dans au moins un n'est plus de 0,05, mais de 0,31.
Pourtant, cette erreur n'est pas difficile à éliminer. Une façon consiste à présenter l'amendement Bonferroni. L'inégalité de Bonferroni nous dit que si vous appliquez les critères k fois
avec un niveau de signification de α, alors la probabilité, dans au moins un cas, de trouver une différence là où elle n'existe pas ne dépasse pas le produit de k par α. D'ici:
α ′ <αk,
où α ′ est la probabilité de confondre au moins une fois les différences. Ensuite, notre problème est résolu très simplement: nous devons diviser notre niveau de signification par la correction de Bonferroni - c'est-à-dire par la multiplicité des comparaisons. Pour trois comparaisons, nous devons prendre les valeurs correspondant à α = 0,05 / 3 = 0,0167 dans les tableaux de test t. Je le répète - c'est très simple, mais cet amendement ne peut être ignoré. Soit dit en passant, vous ne devriez pas vous laisser emporter par cet amendement, même après avoir divisé par 8 les valeurs du critère t sont inutilement plus strictes.
Viennent ensuite les «petites choses» qu’ils ne remarquent souvent pas. Je ne donne pas ici volontairement de formules, afin de ne pas réduire la lisibilité du texte, mais il faut se rappeler que les calculs du critère t varient pour les cas suivants:
Différentes tailles de deux échantillons (en général, n'oubliez pas que dans le cas général, nous comparons deux groupes en utilisant la formule pour le critère à deux échantillons);
Disponibilité d'échantillons dépendants. Ce sont des cas où les données sont mesurées à partir d'un patient à différents intervalles de temps, les données d'un groupe d'animaux avant et après l'expérience, etc.
Enfin, afin que vous puissiez imaginer toute l'étendue de ce qui se passe, je fournirai des données plus récentes sur l'utilisation incorrecte du critère t. Les chiffres concernent 1998 et 2008 pour un certain nombre de revues scientifiques chinoises, et ils parlent d'eux-mêmes. Je veux vraiment que cela se révèle plus négligent dans la conception que les données scientifiques inexactes:
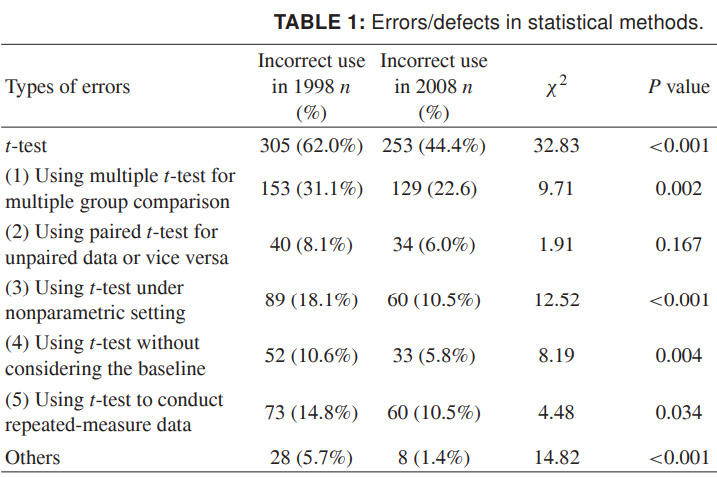
Source: Utilisation abusive des méthodes statistiques dans 10 revues médicales chinoises de premier plan en 1998 et 2008. Shunquan Wu et al, The Scientific World Journal, 2011, 11, 2106–2114
N'oubliez pas que la faible signification des résultats n'est pas une chose aussi triste qu'un faux résultat. Il est impossible de porter au péché scientifique - de fausses conclusions - en déformant les données avec des statistiques mal appliquées.
À propos de l'interprétation logique, y compris incorrecte, des données statistiques, je dirai peut-être séparément.
Lisez bien.