Crayon exotique: détecter un deuxième son dans du graphite ordinaire

Réveillez-vous le matin en chantant des toucans, regardez les prévisions météorologiques et voyez les mêmes +28, enfilez votre short préféré et promenez-vous dans la ville, éloignez les singes impudents de la poubelle, promenez-vous le long de la palmeraie, asseyez-vous sur un banc devant le lac et nourrissez les flamants roses, souvenez-vous de la préparation en hiver et acheter un autre short. Pour quelqu'un, une telle journée n'est pas inhabituelle, mais pour nous (je veux dire les habitants des régions climatiques continentales), c'est un véritable exotisme. Qu'est-ce que le flamant rose et les toucans ont à voir avec la physique, demandez-vous? Et malgré le fait que l'exotisme n'est pas non plus étranger à la physique, se manifestant par des processus, des substances et des phénomènes qui diffèrent en quelque sorte de la norme généralement acceptée. Aujourd'hui, nous allons parler d'un seul de ces phénomènes - le deuxième son, qui a été trouvé dans le graphite ordinaire. Qu'est-ce qui est si exotique que les scientifiques l'ont trouvé et devrions-nous partager leur enthousiasme pour la découverte? Nous trouverons les réponses, où et généralement - non, pas dans Google, mais dans le rapport du groupe de recherche. Allons-y.

Retraite théorique

Le deuxième son est un nom plutôt drôle pour le phénomène, qui ne fait qu'indirectement référence au son lui-même (il est légèrement en contact avec les manches, pour ainsi dire). Le deuxième son est un phénomène de mécanique quantique dans lequel le transfert de chaleur se déroule sous la forme d'une onde, plutôt que de la diffusion habituelle. Le mot «son» est présent au nom de ce processus en raison de la similitude de la propagation des ondes de chaleur avec une propagation similaire des ondes sonores.

Les ondes sonores sont des fluctuations de la densité des molécules d'une substance, mais les ondes du second son sont déjà des fluctuations de la densité des excitations thermiques de type particules (phonons et rotons * ).

Le Roton * est une quasiparticule du superfluide ⁴ He (hélium-4).

Des manifestations antérieures du deuxième son ont été trouvées dans une liste assez petite de substances et à des températures suffisamment basses:

- ² He - hélium liquide ( superfluide * ) obtenu par refroidissement de 4He en dessous de 2,1768 K;

- ⁴ He, ³ He, Bi (bismuth) à une température de 1,2 ... 4,0 K et NaF (fluorure de sodium) à l'état solide d'agrégation à une température de 10 ... 20 K.

La superfluidité * est une propriété d'un fluide à viscosité nulle, ce qui lui permet de s'écouler sans perte d'énergie cinétique. En d'autres termes, une telle substance (liquide quantique) à des températures proches du zéro absolu peut traverser des trous et des capillaires très étroits sans frottement.

Cependant, les scientifiques n'ont pas arrêté de chercher un second son dans d'autres substances. La recherche a donné des résultats - des signes d'un second son ont été trouvés dans du graphite ordinaire à des températures supérieures à 100 K.

Dans leur étude, les scientifiques ont utilisé des mesures optiques de transfert de chaleur dans le graphite avec une échelle de longueur de 5 à 20 microns. Les résultats d'observation sont complètement comparables aux calculs effectués précédemment et indiquant théoriquement la présence d'un second son à une échelle de ~ 1 μm à des températures élevées (jusqu'à la température ambiante).

Les chercheurs nous rappellent que dans les solides non métalliques ordinaires, la chaleur est transférée par les vibrations du réseau ou les phonons * (à ne pas confondre avec les photons). Dans un cristal idéal (pratiquement) à une température d'environ 10 K, les phonons peuvent se propager à des distances microscopiques sans diffusion, ce qui entraîne un transfert de chaleur balistique.

Phonon * est un quantum du mouvement vibratoire d'un atome de cristal.

À température ambiante, la longueur moyenne du transfert de chaleur au phonon est assez faible en raison des vitesses élevées de diffusion phonon-phonon, par conséquent, la chaleur se propage en raison de la diffusion sur des distances macroscopiques.

Le second son, en tant que phénomène, se situe quelque part entre le transfert de chaleur balistique et diffusif. Ce mode intermédiaire est appelé hydrodynamique des phonons. Dans une telle situation, la diffusion phonon-phonon normale se produit beaucoup plus souvent, dans laquelle la quantité de mouvement phonon réduite totale est conservée et le processus de transfert * est moins susceptible de se produire. Processus de transfert * - lorsque les quasiparticules entrent en collision dans des cristaux et que la loi de conservation de la quantité de mouvement est appliquée jusqu'au vecteur de réseau réciproque. Cependant, la diffusion normale seule ne suffit pas pour diffuser le flux de chaleur et ramener le réseau à l'état d'équilibre thermique. Au lieu de cela, la population de phonons se détend vers une distribution de Bose-Einstein «biaisée», caractérisée par une vitesse de dérive non nulle, comparable au flux de molécules dans les gaz. Cela permet aux ondes thermiques (ondes de densité de phonons) de se propager à une vitesse inférieure à la vitesse du son.

Résultats de recherche

En préparation pour les expériences réelles, les scientifiques ont fait des calculs et se sont familiarisés avec certaines prédictions théoriques faites plus tôt. Ils ont constaté qu'un second son devrait se produire dans l'intervalle de temps entre la diffusion normale et le dépassement (τ _N <t <τ _U ). Conformément aux prévisions théoriques, l'échelle nanoseconde de l'expérience a été établie pour le graphène. Et cela complique le processus de recherche en raison de l'impossibilité d'utiliser des capteurs de température conventionnels pour déterminer le transfert de chaleur. Par conséquent, les scientifiques se sont tournés vers les lasers pour obtenir de l'aide. Plus précisément, la méthode des réseaux thermiques de transition ( 1A ) a été utilisée lorsque deux impulsions laser courtes (60 ps) se croisent à la surface de l'échantillon.


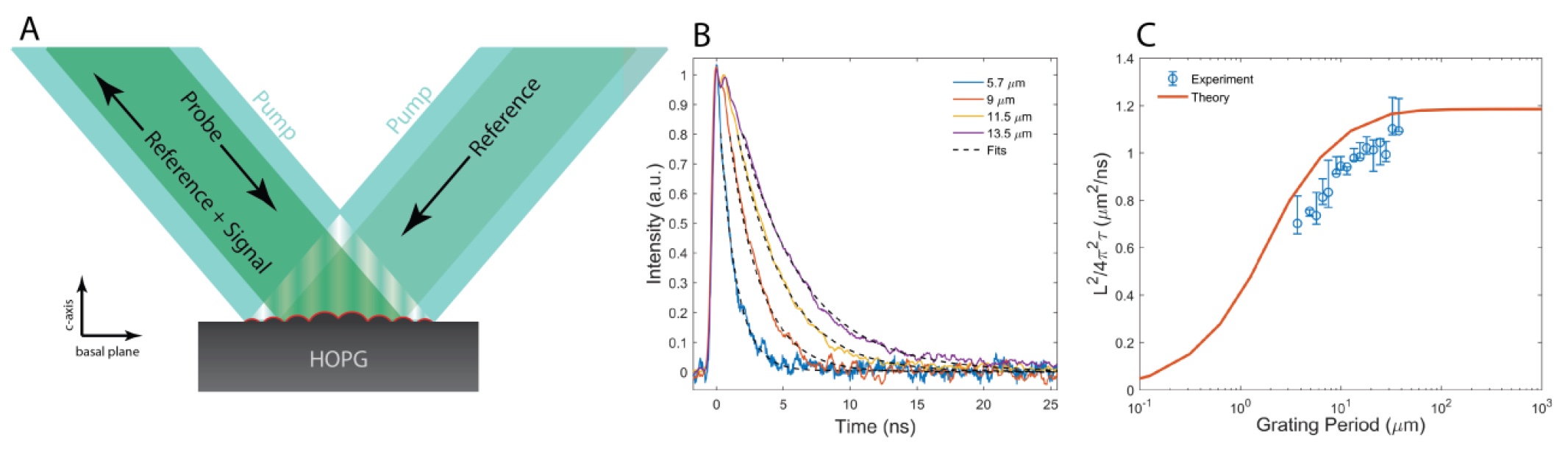Image n ° 1

La «poignée de main» du laser forme une source de chaleur spatialement sinusoïdale, dont la période ( L ) est déterminée par le motif d'interférence optique.

En raison du rayonnement thermique, un «réseau thermique» est formé - un champ de température spatialement sinusoïdal le long de la surface de l'échantillon (∆T (t, z) cos (qx), où q = 2π / L est le vecteur d'onde du réseau thermique). Par la suite, en raison du transfert de chaleur, ce réseau thermique se désintègre. L'expansion thermique crée une modulation sinusoïdale couplée du déplacement de surface ou «pulsation» u (t) cos (qx), qui agit comme un réseau de diffraction de transition pour le rayonnement laser. Ainsi, l'atténuation (dégradation) du réseau de chaleur due au transfert de chaleur est contrôlée par la diffraction en fonction du temps du laser à sonde à onde continue. Le faisceau diffracté est superposé au faisceau de référence de la même source pour une détection hétérodyne optique.

Le graphite pyrolytique hautement orienté était le protagoniste de cette étude, c'est-à-dire un échantillon. L'échantillon était un polycristal avec une taille de grain de ~ 10 μm, et la position de l'axe de tous les grains était perpendiculaire à la surface de l'échantillon lui-même.

Initialement, une lumière de 515 nm a été utilisée sur l'échantillon pour créer le réseau thermique initial à une profondeur de peau optique d'environ 30 nm. Le processus de transfert de chaleur s'est déroulé dans deux directions: le long de la surface de la grille de chaleur (dans le plan) et perpendiculaire à la surface (plan transversal). Le transfert de chaleur dans le plan transversal du graphite était ~ 300 fois plus faible que le transfert dans le plan. Ainsi, la profondeur de diffusion thermique dans le plan transversal est beaucoup plus petite que la position du réseau thermique.

Conformément à la diffusion de la chaleur (τ = L ² / 4π ² ⍺), dans un milieu unidimensionnel, le réseau de transition thermique décroît de façon exponentielle. Cette affirmation a été confirmée dans la pratique: à une température de 300 K, des signes de décroissance exponentielle ( 1B ) ont été détectés. A L (période de réseau) égale à 37,5 µm, une diffusivité thermique de 11 cm ² / s a ​​été obtenue.

Avec une diminution de la période du réseau, la formule de diffusion de chaleur donnée ci-dessus ne correspond pas à une valeur constante de ⍺ (diffusivité thermique). Plus la période de réseau est courte, plus la décroissance / atténuation du réseau thermique de transition ( 1C ) est lente. Et cela est en contradiction avec les prédictions du modèle de diffusion du transfert de chaleur.


Image n ° 2

Le graphique 2A montre des changements significatifs lorsque la température chute à 85 K. À une température de 300 K, les signaux s'humidifient de façon monotone, mais à 85 K, des oscillations amorties se produisent lorsque le signal peut descendre en dessous de zéro. Pour la détection hétérodyne, un changement du signe du signal du réseau de chaleur de transition signifie que la phase spatiale du réseau a changé de π. En d'autres termes, la position des maxima et minima locaux des déplacements de surface (y compris la température) est inversée. Et ce comportement du réseau thermique de transition est comparable à l' onde stationnaire thermique * .

L'onde stationnaire * est un processus ondulatoire dans des systèmes oscillatoires distribués avec alternance et stabilité dans les maxima et minima spatiaux de l'amplitude.

Dans la version à diffusion, le transfert de chaleur se produit des zones plus chaudes vers les zones plus froides, et les maxima et les minima ne peuvent pas être échangés. Autrement dit, cette observation est une caractéristique distinctive de la propagation des ondes de chaleur.

L'encart du graphique 2A montre qu'à mesure que la période du réseau augmente, la fréquence de la dynamique ondulatoire diminue. La relation linéaire observée indique une vitesse de 3200 m / s. Il s'agit d'une observation importante, car souvent les signaux de réseau thermique de transition peuvent contenir des oscillations dues aux ondes acoustiques de surface, mais leur vitesse est beaucoup plus faible. Étant donné que la vitesse des ondes acoustiques de surface est d'environ 1480 m / s, ce qui est proche de la vitesse transversale lente, tandis que la vitesse transversale rapide est de 14700 m / s, et la vitesse longitudinale est encore plus élevée. Il convient également de noter que s'il y avait des ondes acoustiques, elles ne disparaîtraient pas avec une augmentation de la température de fond ou de la période du réseau.

Afin de simuler une telle dynamique, les scientifiques ont appliqué l'équation de transport de Boltzmann linéarisée avec une matrice de diffusion à trois phonons complète dans un réseau thermique de transition unidimensionnel. Auparavant, une méthode similaire était utilisée pour déterminer la conductivité thermique du graphène et du graphite. Cependant, cette technique était quelque peu limitée et ne pourrait pas être appliquée sans de nouvelles études décrivant une méthode de calcul des fonctions de fréquence de Green pour le transport Boltzmann instationnaire et inhomogène. La figure 2B montre précisément ces fonctions vertes qui décrivent la réaction d'une population de phonons à une source de chaleur sous la forme d'une onde plane harmonique.

Les calculs effectués par les scientifiques en tenant compte des méthodes ci-dessus ont permis de comprendre la dépendance temporelle de l'amplitude du réseau thermique. Des calculs à une température de 300 K et à diverses périodes de réseau ont montré l'atténuation exponentielle du réseau thermique de transition, ce qui est parfaitement cohérent avec l'expérience ( 1C ). À une température de 85 K, la fonction de la fréquence Green donne un pic résonant ( 2B ), qui est une caractéristique du second son et conduit à des oscillations d'amortissement ( 2C ). Toutes les données calculées sont totalement comparables à celles expérimentales - même le fait de la disparition du deuxième son à de grandes périodes du réseau thermique de transition.

Les calculs ont montré que la vitesse du second son (en tenant compte de la position du pic de la résonance de fréquence à 2C ) est de 3650 m / s. Un tel indicateur distingue le graphite d'un certain nombre d'autres matériaux où un deuxième son a été détecté. En eux, la vitesse du deuxième son était plus lente que la vitesse minimale des phonons. Le graphite est également surprenant en ce qu'il présente une très faible vitesse du mode acoustique transversal lent. Et l'anharmonicité impressionnante et la densité des états de ce mode conduisent à une diffusion normale intense et créent des conditions pour le transfert hydrodynamique des phonons.


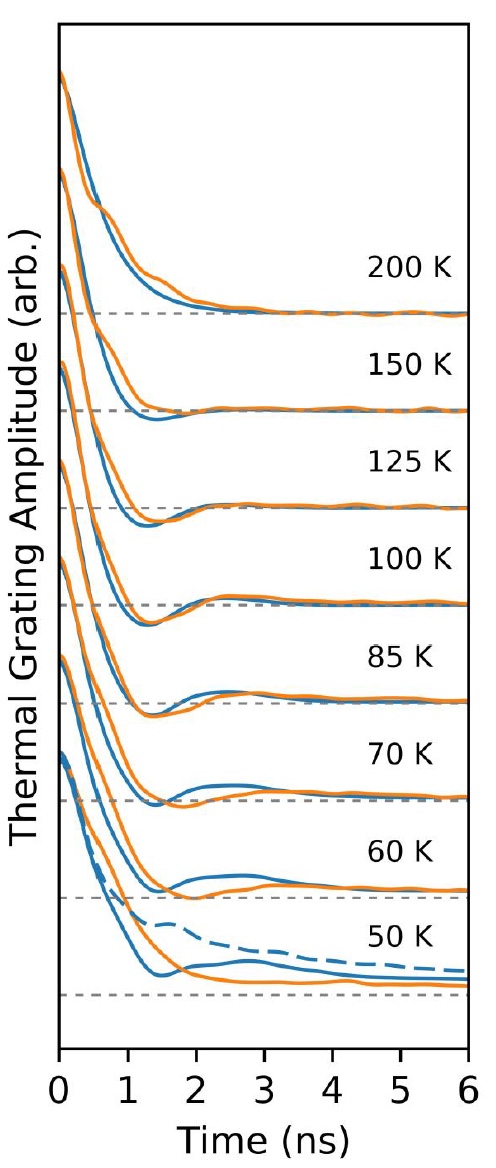Image n ° 3

Le graphique ci-dessus ( n ° 3 ) affiche les données du réseau thermique de transition à une période constante de 10 μm et à différentes températures. Un comportement vibratoire a été observé à 104 K et même à 125 K, mais lorsqu'il atteint une température de 150 K, il disparaît complètement. La même chose se produit lorsque la température descend en dessous de 50 K.

Le graphique montre également une réponse simulée à 50 K en mode balistique, lorsque le taux de diffusion des phonons était réglé à zéro. Et ici, il est clair que l'échec de la réponse en mode balistique disparaît. Autrement dit, la disparition du deuxième son à une température de 50 K correspond à ce qui est attendu lors du passage au mode balistique.


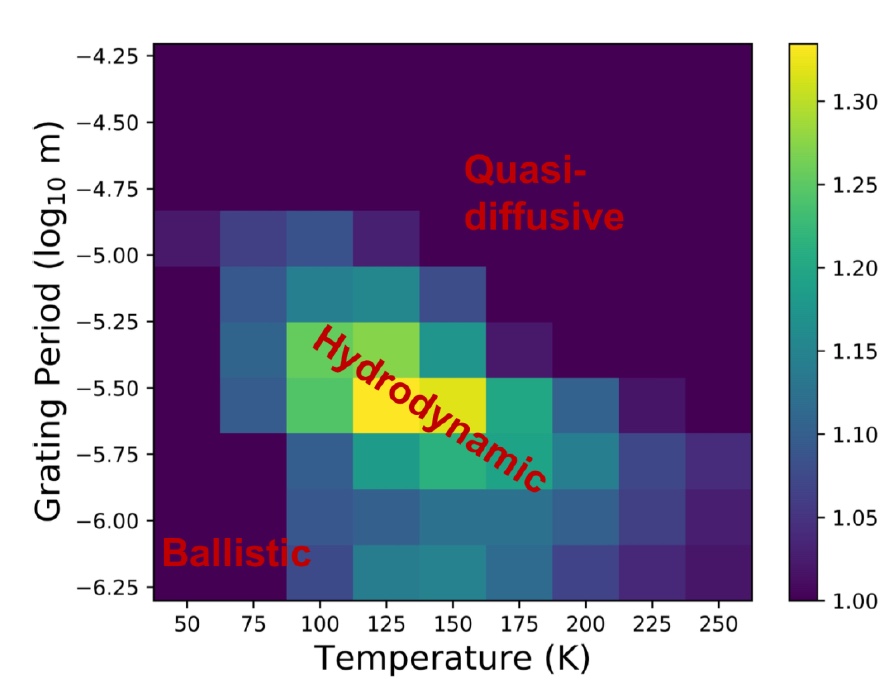Image n ° 4

La modélisation des données a montré que l'apparition d'un deuxième son peut être attendue dans la plage de température de 50 à 250 K. Plus la température est élevée, plus la longueur de transfert de chaleur est courte: à L = 10 μm, la température "plafond" est d'environ 150 K, mais déjà à L = 1,5 μm un second son sera observé jusqu'à 250 K.

Aux basses températures et aux courtes périodes de réseau, la diffusion des phonons disparaît et le transfert de chaleur devient balistique. S'il y a des températures élevées et de longues périodes, le transfert de chaleur passe lentement en mode "quasi-diffusion".

Le graphite excellait également en termes d'isotopes. Autrement dit, plus tôt, le deuxième son n'était observé que dans des solides isotopiquement purs (s'il _n'est pas pris en compte, selon les scientifiques, les observations dans SrTiO ₃ ne _sont pas prises en compte). Mais le graphite utilisé dans l'expérience n'est pas isotopiquement pur, ce qui indique la nature unique de l'hydrodynamique des phonons de cette substance.

Pour une connaissance plus détaillée des nuances, des détails, de la méthodologie et des calculs de l'étude, je vous recommande fortement de consulter le rapport des scientifiques et les documents supplémentaires qui s'y rapportent.

Épilogue

Parfois, des phénomènes ou des propriétés exotiques sont cachés dans les objets les plus ordinaires et les plus banals. Cette étude en est une confirmation. Le second son, étant un phénomène exotique, n'était auparavant observé que dans des substances très «étranges» et dans des conditions très extrêmes.

Les scientifiques considèrent que leurs travaux sont importants pour l'étude générale de l'hydrodynamique des phonons. La compréhension de telles choses permettra d'utiliser le graphite et le graphène comme matériaux dissipant la chaleur en microélectronique. Les scientifiques pensent également que leurs travaux accéléreront l'étude de la manipulation et du contrôle des processus de transport à l'échelle micro et nanométrique.

Nous en savons tellement sur les choses qui nous entourent, mais en même temps, de telles études suggèrent le contraire. Y a-t-il une limite à cette connaissance? Tant qu'il y a la curiosité et l'enthousiasme des scientifiques - non.

Merci de votre attention, restez curieux et bonne semaine de travail, les gars.

Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir des matériaux plus intéressants? Soutenez-nous en passant une commande ou en le recommandant à vos amis, une réduction de 30% pour les utilisateurs Habr sur un analogue unique de serveurs d'entrée de gamme que nous avons inventés pour vous: Toute la vérité sur VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbps à partir de 20 $ ou comment diviser le serveur? (les options sont disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).

VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbit / s jusqu'à l'été gratuitement lorsque vous payez pour une période de six mois, vous pouvez commander ici .

Dell R730xd 2 fois moins cher? Nous avons seulement 2 x Intel Dodeca-Core Xeon E5-2650v4 128 Go DDR4 6x480 Go SSD 1 Gbps 100 TV à partir de 249 $ aux Pays-Bas et aux États-Unis! Pour en savoir plus sur la création d'un bâtiment d'infrastructure. classe utilisant des serveurs Dell R730xd E5-2650 v4 coûtant 9 000 euros pour un sou?