Mountain Car: Résoudre le défi classique avec une formation de renforcement

En règle générale, les modifications d'algorithmes qui reposent sur les caractéristiques spécifiques d'une tâche particulière sont considérées comme moins utiles, car elles sont difficiles à généraliser à une classe de problèmes plus large. Cependant, cela ne signifie pas que de telles modifications ne sont pas nécessaires. De plus, ils peuvent souvent améliorer considérablement le résultat même pour des problèmes classiques simples, ce qui est très important dans l'application pratique des algorithmes. À titre d'exemple, dans ce post, je vais résoudre le problème des voitures de montagne en utilisant une formation de renforcement et montrer que l'utilisation de la connaissance de l'organisation de la tâche peut être résolue beaucoup plus rapidement.

À propos de moi

Je m'appelle Oleg Svidchenko, maintenant j'étudie à l'École des sciences physiques, mathématiques et informatiques de la HSE de Saint-Pétersbourg, avant d'avoir étudié à l'Université de Saint-Pétersbourg pendant trois ans. Je travaille également chez JetBrains Research en tant que chercheur. Avant d'entrer à l'université, j'ai étudié à la SSC de l'Université d'État de Moscou et suis devenu le gagnant de l'Olympiade panrusse des écoliers en informatique au sein de l'équipe de Moscou.

De quoi avons-nous besoin?

Si vous êtes intéressé à essayer une formation de renforcement, le défi Mountain Car est idéal pour cela. Aujourd'hui, nous avons besoin de Python avec les bibliothèques Gym et PyTorch installées, ainsi que des connaissances de base des réseaux de neurones.

Description de la tâche

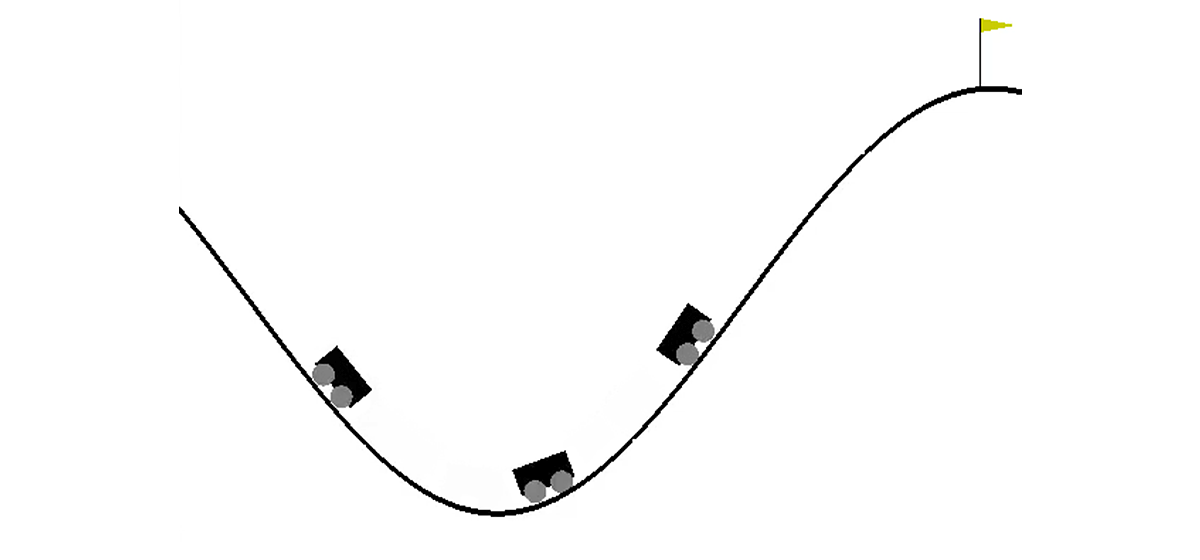
Dans un monde à deux dimensions, une voiture doit monter du creux entre deux collines jusqu'au sommet de la colline de droite. C'est compliqué par le fait qu'elle n'a pas assez de puissance moteur pour vaincre la force de gravité et y entrer du premier coup. Nous sommes invités à former un agent (dans notre cas, un réseau de neurones), qui pourra, en le contrôlant, gravir la colline de droite le plus rapidement possible.

Le contrôle de la machine s'effectue par interaction avec l'environnement. Il est divisé en épisodes indépendants, et chaque épisode est réalisé étape par étape. À chaque étape, l'agent reçoit l'état s et l'environnement r de l'environnement en réponse à l'action a . De plus, le média peut parfois signaler que l'épisode est terminé. Dans ce problème, s est une paire de nombres, dont le premier est la position de la voiture sur la courbe (une coordonnée suffit, car nous ne pouvons pas nous arracher de la surface), et la seconde est sa vitesse sur la surface (avec un signe). La récompense r est un nombre toujours égal à -1 pour cette tâche. De cette façon, nous encourageons l'agent à terminer l'épisode le plus rapidement possible. Il n'y a que trois actions possibles: pousser la voiture vers la gauche, ne rien faire et pousser la voiture vers la droite. Ces actions correspondent à des nombres de 0 à 2. L'épisode peut se terminer si la voiture atteint le sommet de la colline de droite ou si l'agent a fait 200 pas.

Un peu de théorie

Sur Habré, il y avait déjà un article sur DQN dans lequel l'auteur décrivait assez bien toute la théorie nécessaire. Néanmoins, pour en faciliter la lecture, je vais le répéter ici sous une forme plus formelle.

La tâche d'apprentissage par renforcement est définie par un ensemble d'espace d'état S, d'espace d'action A, de coefficient $$$\ gamma$, les fonctions de transition T et les fonctions de récompense R. En général, la fonction de transition et la fonction de récompense peuvent être des variables aléatoires, mais nous allons maintenant considérer une version plus simple dans laquelle elles sont définies de manière unique. L'objectif est de maximiser les récompenses cumulées. $$$\ sum_ {t = 0} ^ {T} r_ {t} \ cdot \ gamma ^ {t}$, où t est le nombre de pas dans le support et T est le nombre de pas dans l'épisode.

Pour résoudre ce problème, nous définissons la fonction de valeur V de l'état s comme la valeur de la récompense cumulative maximale, à condition de commencer dans l'état s. Connaissant une telle fonction, on peut résoudre le problème simplement en passant à chaque étape à s avec la valeur maximale possible. Cependant, tout n'est pas si simple: dans la plupart des cas, nous ne savons pas quelle action nous amènera à l'état souhaité. Par conséquent, nous ajoutons l'action a comme deuxième paramètre de la fonction. La fonction résultante est appelée fonction Q. Il montre quelle récompense cumulative maximale possible nous pouvons obtenir en effectuant l'action a dans l'état s. Mais nous pouvons déjà utiliser cette fonction pour résoudre le problème: étant dans l'état s, nous choisissons simplement un tel que Q (s, a) soit maximal.

En pratique, nous ne connaissons pas la vraie fonction Q, mais nous pouvons l'approcher par différentes méthodes. L'une de ces techniques est le Deep Q Network (DQN). Son idée est que pour chacune des actions, nous approchons la fonction Q à l'aide d'un réseau neuronal.

L'environnement

Passons maintenant à la pratique. Tout d'abord, nous devons apprendre à émuler l'environnement MountainCar. La bibliothèque Gym, qui fournit un grand nombre d'environnements d'apprentissage de renforcement standard, nous aidera à faire face à cette tâche. Pour créer un environnement, nous devons appeler la méthode make sur le module gym en lui passant le nom de l'environnement souhaité en paramètre:

import gym env = gym.make("MountainCar-v0") 

Une documentation détaillée peut être trouvée ici , et une description de l'environnement peut être trouvée ici .
Examinons plus en détail ce que nous pouvons faire avec l'environnement que nous avons créé:

• env.reset() - termine l'épisode en cours et en démarre un nouveau. Renvoie l'état initial.
• env.step(action) - exécute l'action spécifiée. Renvoie un nouvel état, une récompense, si l'épisode est terminé et des informations supplémentaires qui peuvent être utilisées pour le débogage.
• env.seed(seed) - définit une graine aléatoire. Cela dépend de la façon dont les états initiaux seront générés pendant env.reset ().
• env.render() - affiche l'état actuel de l'environnement.

Nous réalisons DQN

DQN est un algorithme qui utilise un réseau de neurones pour évaluer une fonction Q. Dans l' article d'origine, DeepMind a défini l'architecture standard des jeux Atari en utilisant des réseaux de neurones convolutionnels. Contrairement à ces jeux, Mountain Car n'utilise pas l'image comme un état, nous devrons donc déterminer l'architecture nous-mêmes.

Prenons, par exemple, une architecture avec deux couches cachées de 32 neurones chacune. Après chaque couche cachée, nous utiliserons ReLU comme fonction d'activation. Deux nombres décrivant l'état sont fournis à l'entrée du réseau neuronal, et à la sortie, nous obtenons une estimation de la fonction Q.

 import torch.nn as nn model = nn.Sequential( nn.Linear(2, 32), nn.ReLU(), nn.Linear(32, 32), nn.ReLU(), nn.Linear(32, 3) ) target_model = copy.deepcopy(model) #    def init_weights(layer): if type(layer) == nn.Linear: nn.init.xavier_normal(layer.weight) model.apply(init_weights) 

Puisque nous formerons le réseau neuronal sur le GPU, nous devons y charger notre réseau:

 #     CPU,  “cuda”    “cpu” device = torch.device("cuda") model.to(device) target_model.to(device) 

La variable de périphérique sera globale, car nous devrons également charger les données.

Nous devons également définir un optimiseur qui mettra à jour les poids du modèle en utilisant la descente de gradient. Oui, il y en a beaucoup plus d'un.

 optimizer = optim.Adam(model.parameters(), lr=0.00003) 

Maintenant, nous déclarons une fonction qui considérera la fonction d'erreur, le gradient le long de celle-ci et appliquera la descente. Mais avant cela, vous devez télécharger les données du lot sur le GPU:

 state, action, reward, next_state, done = batch #       state = torch.tensor(state).to(device).float() next_state = torch.tensor(next_state).to(device).float() reward = torch.tensor(reward).to(device).float() action = torch.tensor(action).to(device) done = torch.tensor(done).to(device) 

Ensuite, nous devons calculer les valeurs réelles de la fonction Q, cependant, comme nous ne les connaissons pas, nous les évaluerons à travers les valeurs de l'état suivant:

 target_q = torch.zeros(reward.size()[0]).float().to(device) with torch.no_grad(): #     Q-function    target_q = target_model(next_state).max(1)[0].view(-1) target_q[done] = 0 target_q = reward + target_q * gamma 

Et la prédiction actuelle:

 q = model(state).gather(1, action.unsqueeze(1)) 

En utilisant target_q et q, nous calculons la fonction de perte et mettons à jour le modèle:

 loss = F.smooth_l1_loss(q, target_q.unsqueeze(1)) #      optimizer.zero_grad() #     loss.backward() #   . ,       for param in model.parameters(): param.grad.data.clamp_(-1, 1) #    optimizer.step() 

Étant donné que le modèle ne prend en compte que la fonction Q et n'effectue pas d'actions, nous devons déterminer la fonction qui décidera des actions que l'agent effectuera. En tant qu’algorithme décisionnel, nous prenons $$$\ varepsilon$-une politique honteuse. Son idée est que l'agent effectue généralement des actions avec avidité, en choisissant le maximum de la fonction Q, mais avec probabilité $$$\ varepsilon$il prendra une action aléatoire. Des actions aléatoires sont nécessaires pour que l'algorithme puisse examiner les actions qu'il n'aurait pas effectuées guidées uniquement par une politique gourmande - ce processus est appelé exploration.

 def select_action(state, epsilon, model): if random.random() < epsilon: return random.randint(0, 2) return model(torch.tensor(state).to(device).float().unsqueeze(0))[0].max(0)[1].view(1, 1).item() 

Puisque nous utilisons des lots pour former le réseau neuronal, nous avons besoin d'un tampon dans lequel nous stockerons l'expérience d'interagir avec l'environnement et d'où nous choisirons des lots:

 class Memory: def __init__(self, capacity): self.capacity = capacity self.memory = [] self.position = 0 def push(self, element): """    """ if len(self.memory) < self.capacity: self.memory.append(None) self.memory[self.position] = element self.position = (self.position + 1) % self.capacity def sample(self, batch_size): """    """ return list(zip(*random.sample(self.memory, batch_size))) def __len__(self): return len(self.memory) 

Décision naïve

Tout d'abord, déclarez les constantes que nous utiliserons dans le processus d'apprentissage et créez un modèle:

 #  model   target model target_update = 1000 #  ,      batch_size = 128 #   max_steps = 100001 #  exploration max_epsilon = 0.5 min_epsilon = 0.1 #    memory = Memory(5000) model, target_model, optimizer = create_new_model() 

Malgré le fait qu'il serait logique de diviser le processus d'interaction en épisodes, pour décrire le processus d'apprentissage, il est plus pratique pour nous de le diviser en étapes séparées, car nous voulons faire une étape de descente de gradient après chaque étape de l'environnement.

Parlons plus en détail de ce à quoi ressemble une étape de l'apprentissage ici. Nous supposons que nous faisons maintenant une étape avec le nombre d'étapes max_steps et l'état actuel. Faire ensuite l'action avec $$$\ varepsilon$-les politiques punitives ressembleraient à ceci:

 epsilon = max_epsilon - (max_epsilon - min_epsilon)* step / max_steps action = select_action(state, epsilon, model) new_state, reward, done, _ = env.step(action) 

Ajoutez immédiatement l'expérience acquise à la mémoire et commencez un nouvel épisode si l'actuel est terminé:

 memory.push((state, action, reward, new_state, done)) if done: state = env.reset() done = False else: state = new_state 

Et nous prendrons l'étape de descente de gradient (si, bien sûr, nous pouvons déjà collecter au moins un lot):

 if step > batch_size: fit(memory.sample(batch_size), model, target_model, optimizer) 

Reste maintenant à mettre à jour target_model:

 if step % target_update == 0: target_model = copy.deepcopy(model) 

Cependant, nous aimerions également suivre le processus d'apprentissage. Pour ce faire, nous jouerons un épisode supplémentaire après chaque mise à jour de target_model avec epsilon = 0, stockant le prix total dans le tampon rewards_by_target_updates:

 if step % target_update == 0: target_model = copy.deepcopy(model) state = env.reset() total_reward = 0 while not done: action = select_action(state, 0, target_model) state, reward, done, _ = env.step(action) total_reward += reward done = False state = env.reset() rewards_by_target_updates.append(total_reward) 

Exécutez ce code et obtenez quelque chose comme ce graphique:

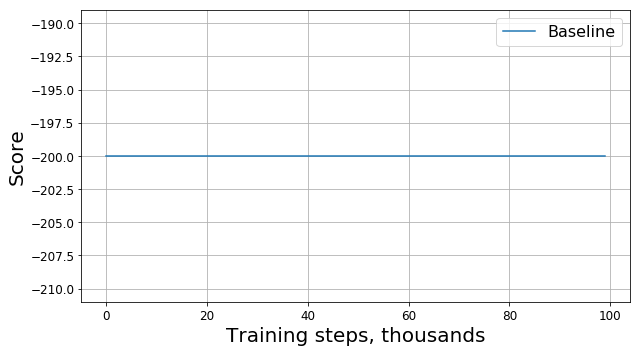
Qu'est-ce qui a mal tourné?

Est-ce un bug? Est-ce le mauvais algorithme? S'agit-il de mauvais paramètres? Pas vraiment. En fait, le problème est dans la tâche, à savoir dans la fonction de la récompense. Examinons-le de plus près. À chaque étape, notre agent reçoit une récompense de -1, et cela se produit jusqu'à la fin de l'épisode. Une telle récompense motive l'agent à terminer l'épisode le plus rapidement possible, mais en même temps ne lui dit pas comment le faire. Pour cette raison, la seule façon d'apprendre à résoudre un problème dans une telle formulation pour un agent est de le résoudre plusieurs fois en utilisant l'exploration.

Bien sûr, on pourrait essayer d'utiliser des algorithmes plus complexes pour étudier l'environnement au lieu du nôtre $$$\ varepsilon$-des politiques honteuses. Cependant, premièrement, en raison de leur application, notre modèle deviendra plus complexe, ce que nous aimerions éviter, et deuxièmement, pas le fait qu'ils fonctionneront assez bien pour cette tâche. Au lieu de cela, nous pouvons éliminer la source du problème en modifiant la tâche elle-même, à savoir en changeant la fonction de récompense, c'est-à-dire en appliquant ce qu'on appelle la mise en forme des récompenses.

Accélérer la convergence

Notre connaissance intuitive nous dit que pour monter la colline, vous devez accélérer. Plus la vitesse est élevée, plus l'agent est proche de résoudre le problème. Vous pouvez lui en parler, par exemple, en ajoutant un module de vitesse avec un certain coefficient à la récompense:

  modified_reward = récompense + 10 * abs (new_state [1]) 

En conséquence, une ligne dans la fonction correspond

  memory.push ((état, action, récompense, new_state, done)) 

devrait être remplacé par

  memory.push ((état, action, modification_reward, nouvel_état, terminé)) 

Examinons maintenant le nouveau tableau (il présente le prix original sans modifications):


Ici, RS est l'abréviation de Reward Shaping.

Est-ce bon de faire ça?

Les progrès sont évidents: notre agent a clairement appris à monter la colline, car le prix a commencé à différer de -200. Il ne reste qu'une question: si nous changeons la fonction de la récompense, nous changeons également la tâche elle-même, la solution au nouveau problème que nous avons trouvé sera-t-elle bonne pour l'ancien problème?

Pour commencer, nous comprenons ce que signifie la «bonté» dans notre cas. Pour résoudre le problème, nous essayons de trouver la politique optimale - celle qui maximise la récompense totale pour l'épisode. Dans ce cas, nous pouvons remplacer le mot «bon» par le mot «optimal», car nous le recherchons. Nous espérons également avec optimisme que tôt ou tard notre DQN trouvera la solution optimale pour le problème modifié, et ne restera pas bloqué au maximum local. Ainsi, la question peut être reformulée comme suit: si nous modifions la fonction de la récompense, nous avons également changé le problème lui-même, la solution optimale au nouveau problème que nous avons trouvé sera-t-elle optimale pour l'ancien problème?

Il s'avère que nous ne pouvons pas fournir une telle garantie dans le cas général. La réponse dépend de la façon dont nous avons changé exactement la fonction de la récompense, comment elle a été organisée plus tôt et comment l'environnement lui-même est organisé. Heureusement, il y a un article dont les auteurs ont étudié comment le changement de la fonction de la récompense affecte l'optimalité de la solution trouvée.

Premièrement, ils ont trouvé toute une classe de changements «sûrs» qui sont basés sur la méthode potentielle: $$$R ’= R + (\ gamma \ cdot \ Phi (new \ _state) - \ Phi (state))$où $$$\ Phi$- potentiel, qui ne dépend que de l'état. Pour de telles fonctions, les auteurs ont pu prouver que si la solution du nouveau problème est optimale, alors pour l'ancien problème elle l'est aussi.

Deuxièmement, les auteurs ont montré que pour tout autre $$$R ’= R + F (s, a)$il existe un tel problème, la fonction de récompense R et la solution optimale au problème modifié, que cette solution n'est pas optimale pour le problème d'origine. Cela signifie que nous ne pouvons pas garantir la qualité de la solution que nous avons trouvée si nous utilisons un changement qui n'est pas basé sur la méthode potentielle.

Ainsi, l'utilisation de fonctions potentielles pour modifier la fonction de récompense ne peut que modifier le taux de convergence de l'algorithme, mais n'affecte pas la solution finale.

Accélérez correctement la convergence

Maintenant que nous savons comment changer la récompense en toute sécurité, essayons à nouveau de modifier la tâche, en utilisant la méthode potentielle au lieu d'heuristiques naïves:

  modified_reward = récompense + 300 * (gamma * abs (new_state [1]) - abs (état [1])) 

Regardons le calendrier du prix original:



Il s'est avéré qu'en plus d'avoir des garanties théoriques, la modification de la récompense à l'aide de fonctions potentielles a également considérablement amélioré le résultat, en particulier au début. Bien sûr, il est possible qu'il soit possible de sélectionner des hyperparamètres plus optimaux (graine aléatoire, gamma et autres coefficients) pour former l'agent, mais la mise en forme des récompenses augmente néanmoins considérablement le taux de convergence du modèle.

Postface

Merci d'avoir lu jusqu'au bout! J'espère que vous avez apprécié cette petite excursion axée sur la pratique dans l'apprentissage renforcé. Il est clair que Mountain Car est une tâche «jouet», cependant, comme nous avons pu le constater, apprendre à un agent à résoudre même une tâche apparemment simple d'un point de vue humain peut être difficile.