La couleur de la lune et du soleil de l'espace dans les valeurs de RVB et de température de couleur

Il semblerait que la question de la couleur de la Lune et du Soleil depuis l'espace est si simple pour la science moderne que dans notre siècle il ne devrait pas y avoir de problème avec une réponse. Nous parlons de couleurs lors de l'observation depuis l'espace, car l'atmosphère entraîne un changement de couleur dû à la diffusion de la lumière de Rayleigh. "Sûrement quelque part dans l'encyclopédie à ce sujet en détail, en chiffres, cela a longtemps été écrit", dites-vous. Eh bien, en ce moment, essayez de rechercher sur Internet ces informations. Cela at-il fonctionné? Probablement pas. Le maximum que vous trouverez est quelques mots que la lune a une teinte brunâtre et le soleil est rougeâtre. Mais vous ne trouverez pas d'informations si ces nuances sont visibles à l'œil humain ou non, en particulier les valeurs des couleurs en RVB ou au moins les températures de couleur. Mais ensuite, vous trouverez un tas de photos et de vidéos où la Lune de l'espace est montrée absolument grise, principalement dans les photographies du programme américain Apollo, et où le Soleil de l'espace est montré en blanc et même en bleu.

Mon opinion purement personnelle n'est qu'une conséquence de l'ingérence de la politique dans la science. Après tout, les couleurs de la Lune et du Soleil depuis l'espace sont directement liées aux vols des Américains vers la Lune.

J'ai cherché dans de nombreux articles et livres scientifiques à la recherche d'informations sur la couleur de la lune et du soleil depuis l'espace. Heureusement, il s'est avéré que même s'ils n'ont pas de réponse directe en RVB, il existe des informations complètes sur la densité spectrale du rayonnement solaire et la réflectivité de la lune dans le spectre. Cela suffit pour obtenir les couleurs exactes dans les valeurs RVB. Vous avez juste besoin de calculer soigneusement ce que j'ai fait. Dans cet article, je partagerai les résultats des calculs avec vous et, bien sûr, je vous parlerai en détail des calculs eux-mêmes. Et vous verrez la lune et le soleil de l'espace dans de vraies couleurs!

J'ai effectué les calculs dans le programme Mathcad et, en conséquence, les fragments de code seront dans le langage de programmation intégré, qui est tout à fait approprié comme pseudo-code compréhensible par tous.

Dans le même temps, je vais vous dire en détail quel est le modèle de couleur RVB, avec lequel, je pense, vous êtes tous familiers. Cette question n'est pas non plus tout à fait simple. Par exemple, essayez de répondre aux deux questions suivantes. Soit la couleur rgb (120,80,100) donnée.
1) Quelles sont les valeurs de la couleur RVB, qui est 2 fois plus sombre que celle spécifiée?
2) Quelles sont les valeurs RVB pour le gris qui ont la même luminosité que celle donnée?
Il semblerait que ce qu'il y a à penser, diviser par 2 dans le premier cas, soit rgb (60,40,50) et moyen dans le second cas, c'est-à-dire rgb (100,100,100) . Hélas, les bonnes réponses sont: 1) rgb (86.56.71) ; 2) RVB (92,92,92) . Vous découvrirez pourquoi les réponses ne sont que cela.

Je parlerai également de la température de couleur et de la façon de la calculer.

Espace colorimétrique XYZ

XYZ est un modèle de couleur de référence défini au sens mathématique strict par la CIE (Commission internationale de l'éclairage) en 1931. Le modèle CIE XYZ est un modèle maître de presque tous les autres modèles de couleurs utilisés dans les domaines techniques. La couleur XYZ est définie comme suit:

$$

$$X = \ int _ {390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {x}} (\ lambda) \, d \ lambda \\ Y = \ int _ { 390 \, nm} ^ {830 \, nm} I (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda \\ Z = \ int _ {390 \, nm} ^ ^ { 830 \, nm} I (\ lambda) \, {\ overline {z}} (\ lambda) \, d \ lambda$$

où $$$I (\ lambda)$ - la densité spectrale de toute quantité photométrique d'énergie (par exemple, flux de rayonnement, luminosité énergétique, etc., en termes absolus ou relatifs) dans la gamme de longueurs d'onde de 390 à 830 nm (selon 2006, en 1931, la gamme était de 380 à 780 nm ); $$${\ overline {x}} (\ lambda)$ , $$${\ overline {y}} (\ lambda)$ , $$${\ overline {z}} (\ lambda)$ - fonctions de correspondance des couleurs. De plus, ce qui est important pour nous, la coordonnée Y correspond à la luminosité visuelle du signal.

Les données de la fonction de correspondance des couleurs que j'ai téléchargées à partir d'ici: [ 1 ]. Là, les fonctions de correspondance des couleurs sont définies pour le champ de vision de 2 degrés et 10 degrés . J'ai décidé d'effectuer des calculs pour les deux cas, de comparer les résultats et de m'assurer que, comme prévu, les coordonnées de couleur diffèrent légèrement. Naturellement, j'ai utilisé ces fonctions avec la résolution maximale fournie, c'est-à-dire avec un pas de 0,1 nm . Les graphiques des fonctions de correspondance des couleurs sont les suivants:



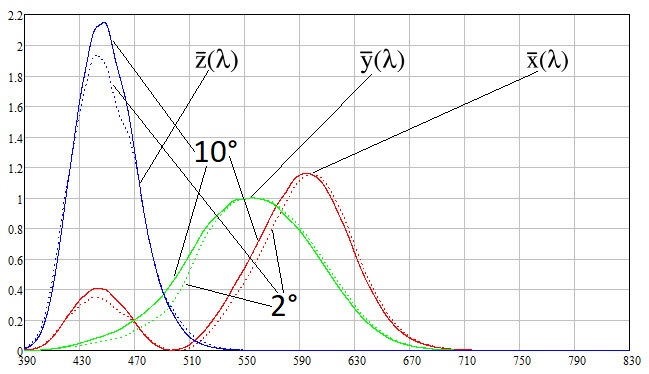
Les graphiques montrent qu'au-dessus de 710 nm, les fonctions deviennent négligeables dans le sens où, lors de l'observation d'une couleur proche du blanc, la densité spectrale dans la plage au-dessus de 710 nm n'apporte presque aucune contribution. Bien que nous sachions que la lumière visible se situe dans la plage allant jusqu'à 780 nm , nous devons comprendre qu'il s'agit d'un rayonnement monochromatique. Je suis tout cela dû au fait que dans certains calculs, j'ai dû extrapoler les données manquantes de la réflectivité de la lune juste à la plage où les fonctions de correspondance des couleurs sont essentiellement petites. Par conséquent, une éventuelle erreur d'extrapolation ne conduit pas à une erreur notable dans les couleurs calculées.

Je calcule les intégrales indiquées par la méthode trapézoïdale :


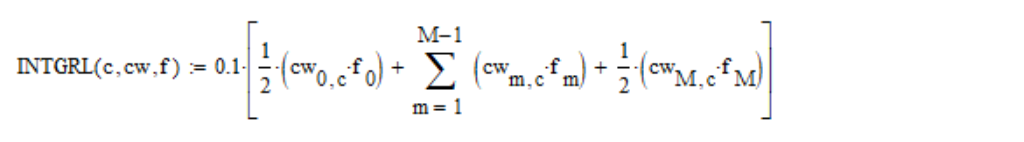
où c est le numéro de coordonnée de l'espace colorimétrique (1, 2, 3 pour X, Y, Z, respectivement); cw - tableau des fonctions de correspondance des couleurs; f est la densité spectrale; M = (830-390) /0.1=4400 - le nombre d'étapes de la grille.

Les fonctions de correspondance des couleurs correctes ont la propriété que la zone sous les trois courbes est la même:

$$

$$\ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {x}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {y}} (\ lambda) \, d \ lambda \, = \ int _ {390 \, nm} ^ {830 \, nm} \, {\ overline {z}} (\ lambda) \, d \ lambda$$

Ceci est fait pour que le spectre uniforme ait les mêmes coordonnées XYZ. Vérifiez si cette propriété détient:


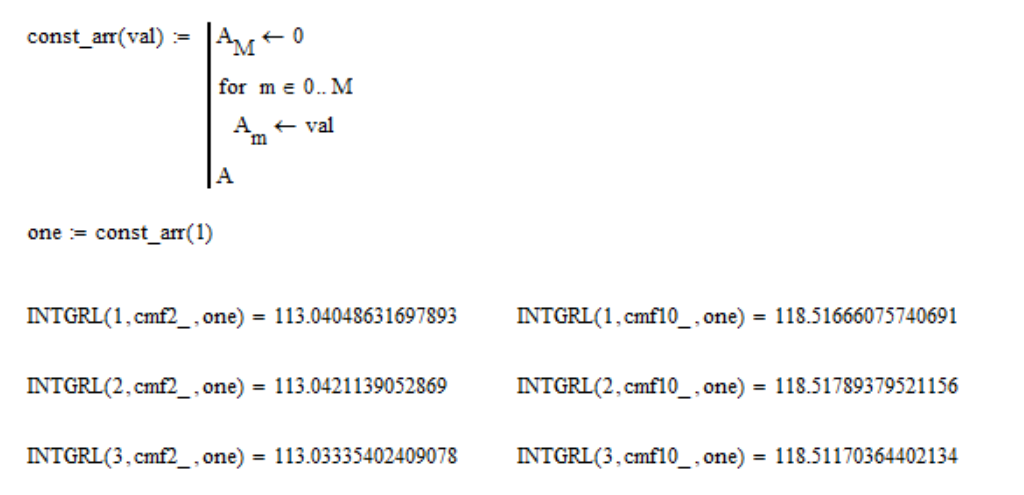
où l'on est un tableau de 1; cmf2_ et cmf10_ sont des tables de fonctions de correspondance des couleurs pour le champ de vision de 2 degrés et 10 degrés , respectivement. Comme vous pouvez le voir, la propriété est satisfaite avec une précision de 0,01% , ce qui est très bien. Mais encore, nous renormalisons les fonctions pour la fidélité:

Normalisation de la luminosité

Considérez le fonctionnement d'un appareil photo numérique. L'élément principal d'un appareil photo numérique est une matrice, qui se compose de photocapteurs. Lors de la projection d'une image sur une matrice, une charge électrique est proportionnelle à chacun de ses photocapteurs, qui est proportionnelle à l'énergie de rayonnement du photocapteur. Les photocapteurs capturent la luminosité d'un élément d'image sans aucune information sur sa couleur. Pour obtenir des informations sur la couleur, la matrice des photocapteurs est recouverte d'une matrice de filtres lumineux miniatures sur le dessus. Ces filtres servent de fonctions de correspondance des couleurs. Chaque pixel est composé de plusieurs photocapteurs, qui au total se superposent toutes sortes de filtres.

Donc, en fonction $$$I (\ lambda)$ nous devons prendre la densité spectrale de l'énergie d'irradiation d'un pixel. Une telle densité spectrale peut être représentée comme

$$

$$I (\ lambda) = coef \ cdot illumination (\ lambda) \ cdot albedo (\ lambda)$$

où l' éclairage est la densité de rayonnement spectrale de la source de lumière ; albédo - réflectivité de la surface de l'objet photographié; coef - un certain coefficient constant, qui est déterminé par le temps d'exposition, l'ouverture, la distance de la source de lumière à l'objet photographié et d'autres facteurs. La réflectance fait référence à l' albédo apparent , qui est défini comme le rapport de la luminosité d'un élément de surface plane éclairé par un faisceau de rayons parallèle à la luminosité d'une surface complètement blanche perpendiculaire aux rayons.

Imaginez maintenant que nous faisons le travail d'un posemètre photo, avec lequel le photographe règle la vitesse d'obturation et l'ouverture sur l'appareil photo. En d'autres termes, nous devons choisir la valeur de coef pour que l'image se révèle normale en luminosité, ni trop sombre, ni trop lumineuse. Imaginez que derrière l'objet photographié se trouve un écran complètement blanc. L' albédo de réflectance d' un tel écran est par définition égal à 1 à toutes les longueurs d'onde. Réglez la valeur coef de sorte que la luminosité visuelle Y de cet écran dans l'image soit 1. Pourquoi 1? Parce que dans le modèle de couleur RVB, la valeur de luminosité maximale possible est 1, ce qui est atteint avec RVB (255 , 255 , 255) , c'est-à-dire avec la couleur blanche. J'en parlerai plus tard. Étant donné que les corps ordinaires sont de couleur plus sombre qu'un écran complètement blanc, les images auront une luminosité normale. De ces considérations, nous obtenons l'expression suivante pour coef :

$$

$$coef = \ frac {1} {\ int _ {390 \, nm} ^ {830 \, nm} illumination (\ lambda) \, {\ overline {y}} (\ lambda) \, d \ lambda}$$

Il convient de noter qu'une telle normalisation ne garantit pas que la valeur de chaque coordonnée RVB sera inférieure ou égale à 255. Par exemple, si vous photographiez un écran absolument blanc avec une source de lumière rouge, la couleur RVB montera en flèche.

Donc, je calcule les coordonnées de l'espace colorimétrique XYZ comme suit:


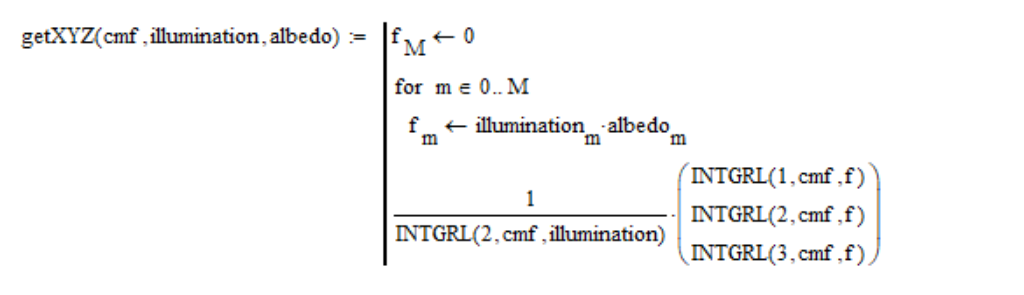
Nous devons en quelque sorte exprimer la couleur du soleil. Nous ne pouvons pas le photographier directement, et dans notre modèle mathématique, nous n'avons pas fourni un cas aussi extrême. De toute évidence, nous devons photographier la surface blanche éclairée par le soleil. Étant donné que le Soleil de l'espace a une teinte rougeâtre, alors, comme je l'ai dit, la couleur d'un écran absolument blanc disparaît de l'échelle. Par conséquent, nous devons prendre la surface plus sombre. J'ai constaté expérimentalement que vous devez prendre du papier blanc avec un albédo de 0,91. Vous ne pouvez pas prendre plus d'albédo, il commence à rouler. Ainsi, afin d'obtenir la couleur du soleil, je viens de définir la valeur de l' albédo à 0,91 à toutes les longueurs d'onde dans la formule ci-dessus:

Espace colorimétrique SRGB

L'espace colorimétrique le plus courant utilisant le modèle RVB est sRGB. Par conséquent, lorsque l'on parle de RVB sans précision, cela signifie l'espace colorimétrique sRGB, qui est la norme pour représenter le spectre de couleurs à l'aide du modèle RVB. Cette norme a été créée par l'International Color Consortium (ICC) en 1996 pour unifier l'utilisation du modèle RVB dans les moniteurs, les imprimantes et les sites Internet. Regardons cette norme, dont une description est disponible sur [ 2 ].

La conversion de XYZ en sRGB se déroule en trois étapes. Tout d'abord, les coordonnées XYZ sont converties en coordonnées RVB linéaires, puis les coordonnées linéaires sont converties en coordonnées RVB non linéaires, et enfin les coordonnées non linéaires sont converties en coordonnées RVB 8 bits, qui, en fait, sont les coordonnées de l'espace colorimétrique sRGB.

La conversion des coordonnées XYZ en coordonnées RVB linéaires est la suivante:



et l'inverse est comme ceci:



Je me demande d'où viennent ces étranges nombres dans les matrices carrées? Et ils sont issus de la recommandation UIT-R BT.709 [ 3 ]. Désignons la première matrice carrée par XYZ_to_RGB , et la seconde par RGB_to_XYZ . De toute évidence, ils sont mutuellement inverses. La Recommandation UIT-R BT.709 spécifie les exigences qui doivent être satisfaites pour la deuxième matrice. À partir de ces exigences, nous pouvons calculer uniquement la deuxième matrice, et la première est égale à la matrice inverse de la seconde.

Nous introduisons les fonctions suivantes:

$$

$$XYZ (R, G, B) = RGB \ _to \ _XYZ \ cdot {\ begin {bmatrix} R \\ G \\ B \ end {bmatrix}} \\ W (R, G, B) = XYZ_1 (R , G, B) + XYZ_2 (R, G, B) + XYZ_3 (R, G, B) \\ xy (R, G, B) = \ frac {1} {W (R, G, B)} \ cdot {\ begin {bmatrix} XYZ_1 (R, G, B) \\ XYZ_2 (R, G, B) \ end {bmatrix}}$$

Les exigences de la recommandation UIT-R BT.709 prennent alors la forme suivante:

$$

$$xy (1,0,0) = {\ begin {bmatrix} 0,64 \\ 0,33 \ end {bmatrix}}, \; xy (0,1,0) = {\ begin {bmatrix} 0,30 \\ 0,60 \ end {bmatrix}}, \; xy (0,0,1) = {\ begin {bmatrix} 0,15 \\ 0,06 \ end {bmatrix}} \\ xy (1,1,1) = {\ begin {bmatrix} 0,3127 \\ 0,3290 \ end {bmatrix }}$$

Nous avons 8 équations, lorsque nous avons 9 éléments inconnus de la matrice RGB_to_XYZ , c'est-à-dire qu'il manque une autre équation. Et l'équation manquante était implicitement établie, je devais la deviner moi-même. L'essence de cette équation est que pour le blanc, la luminosité visuelle Y doit être égale à 1:

$$

$$XYZ_2 (1,1,1) = 1$$

J'ai trouvé la solution exacte à ces équations en nombres rationnels:


Si j'arrondis les nombres dans mon résultat à quatre décimales, alors nous obtenons exactement ces nombres très étranges dans la norme de l'International Color Consortium. Dans mes calculs, j'utilise non pas des matrices arrondies, mais celles exactes ci-dessus (pour autant que les nombres à virgule flottante double précision le permettent).

Ainsi, les coordonnées linéaires de RVB basées sur le tableau des fonctions de correspondance des couleurs (cmf), la densité spectrale du rayonnement (illumination) et la réflectance (albédo) que je calcule comme suit:



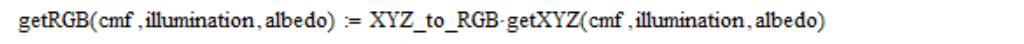
J'utilise également des coordonnées RVB linéaires, moyennées sur un champ de vision de 2 degrés et 10 degrés :



À partir des coordonnées linéaires de RVB, la luminosité visuelle Y est calculée à l'aide de la formule suivante (par défaut, les tableaux Mathcad sont numérotés à partir de l'élément zéro):


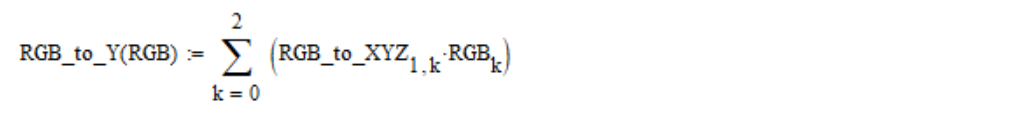
Nous continuons de démonter la norme. Chaque coordonnée RVB linéaire est convertie en non linéaire à l'aide de la fonction lin2bit non linéaire, et vice versa, bit2lin, qui sont définies comme suit:


Les graphiques de ces fonctions ressemblent à ceci:



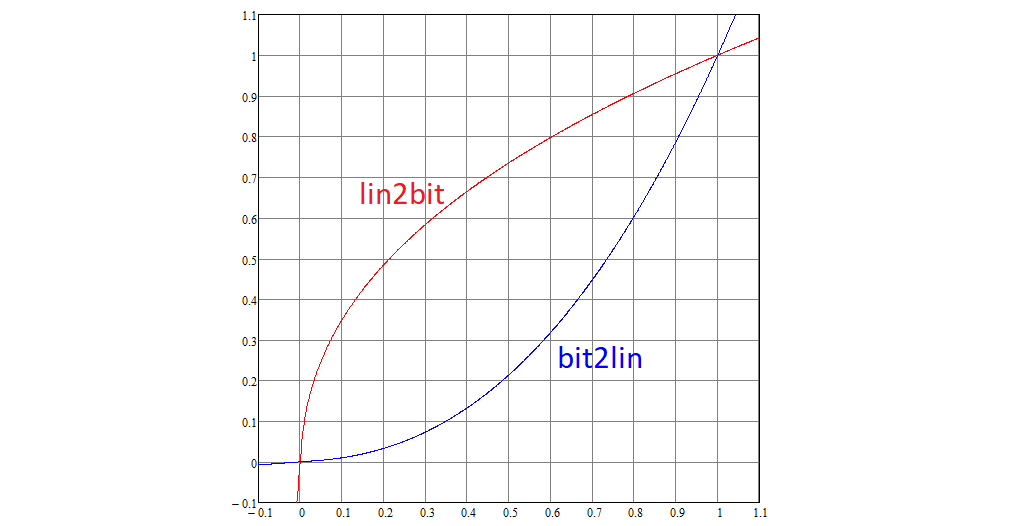
Notez que 0 convertit en 0, 1 en 1.

En fin de compte, les coordonnées RVB non linéaires sont converties en 8 bits en multipliant par 255, puis arrondies en entiers.

Ainsi, j'ai défini les fonctions suivantes pour convertir les coordonnées RVB linéaires en 8 bits et vice versa:

Nous sommes maintenant prêts à résoudre le problème depuis l'introduction. Je vous rappelle la condition.

Soit la couleur rgb (120,80,100) donnée.
1) Quelles sont les valeurs de la couleur RVB, qui est 2 fois plus sombre que celle spécifiée?
2) Quelles sont les valeurs RVB pour le gris qui ont la même luminosité que celle donnée?

Solution:

Réponses: 1) rgb (86.56.71) ; 2) RVB (92,92,92) .

Température de couleur

La température de couleur de la source lumineuse, mesurée en Kelvin, est déterminée par la température d'un corps complètement noir situé sur le nuancier au même endroit que la source de rayonnement en question. Si la source lumineuse ne tombe pas sur la courbe de Planck (une courbe qui est déterminée par l'ensemble des points de couleur d'un corps noir à différentes températures), une température de couleur corrélée est utilisée pour la caractériser. Cette valeur est également mesurée en Kelvin et est déterminée par la température d'un corps complètement noir, dont la couleur est aussi proche que possible de la couleur de la source lumineuse. Pour trouver la température de couleur corrélée de la source de rayonnement sur le nuancier construit dans les coordonnées (u, v) , le point le plus proche de la source sur la courbe de Planck (c'est-à-dire la distance géométrique la plus courte) est déterminé. La température du corps noir situé à ce point correspondra à la température de couleur corrélée de la source considérée [ 4 ].

Pour un corps de température T complètement noir, la puissance de rayonnement par unité de surface de la surface rayonnante dans un intervalle de longueur d'onde unitaire est exprimée par la loi de Planck :

$$

$$R (\ lambda, T) = \ frac {2 \ pi h c ^ 2} {\ lambda ^ 5} \ frac {1} {e ^ {h c / \ lambda k T} -1}$$

En conséquence, je calcule la densité de rayonnement spectrale d'un corps absolument noir comme suit (dans la colonne zéro du tableau des fonctions d'appariement des couleurs cmf2, il y a des longueurs d'onde en nanomètres):



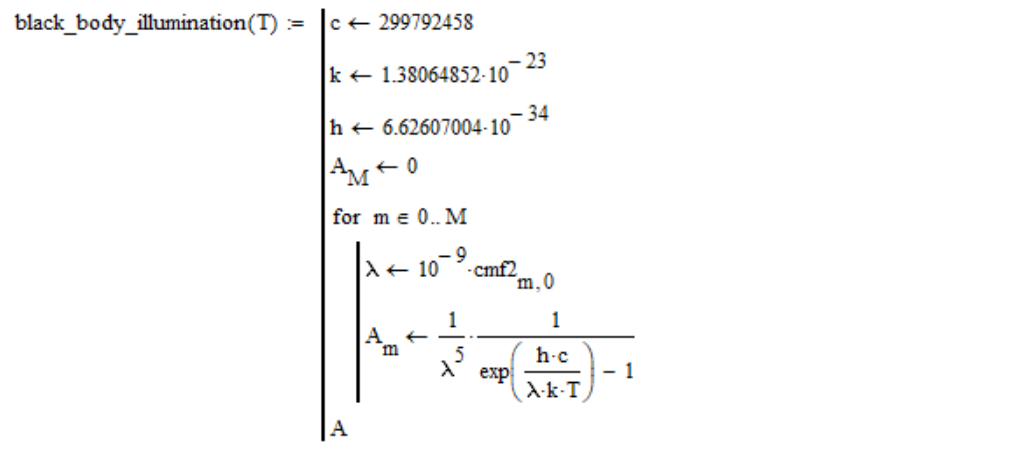
Veuillez noter que j'ai omis le facteur constant, car il diminue toujours avec une normalisation supplémentaire par la luminosité (la luminosité de la source lumineuse n'affecte pas la température de couleur).

Ensuite, je calcule les coordonnées linéaires de RVB:



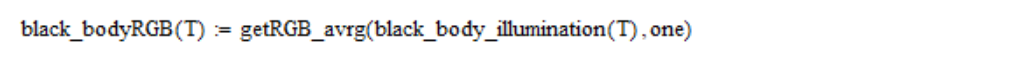
Les coordonnées linéaires RVB sont converties en coordonnées (u, v) comme suit:



Sur le plan (u, v), la distance géométrique entre les points de la couleur considérée et la couleur du corps noir d'une température T donnée est calculée:



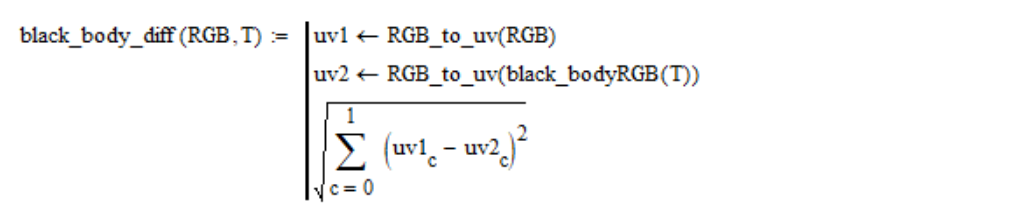
Par exemple, pour une source de lumière blanche standard, la dépendance de cette distance à la température ressemble à ceci:



La valeur de T à laquelle cette dépendance a un minimum est la température de couleur de la source lumineuse en question.

La densité spectrale du rayonnement du soleil

J'ai téléchargé les données de la densité spectrale du rayonnement solaire en l'absence de l'atmosphère d'ici: [ 5 ]. La source lumineuse correspondant au Soleil depuis l'espace, je désignerai désormais E490. De plus, à titre de comparaison, dans les calculs, je considère la source de lumière standard D65 . Cette source représente la lumière blanche. Je la regarde pour montrer à quoi ressemblerait la lune si le soleil était blanc. J'ai téléchargé ici les données de la densité spectrale de rayonnement d'une source lumineuse standard D65: [ 6 ].

Comme indiqué ci-dessous, les sources lumineuses D65 et E490 ont des températures de couleur de 6467K et 5912K, respectivement. Les densités de rayonnement spectral des sources lumineuses D65, E490 et des corps absolument noirs des températures correspondantes sont les suivantes:



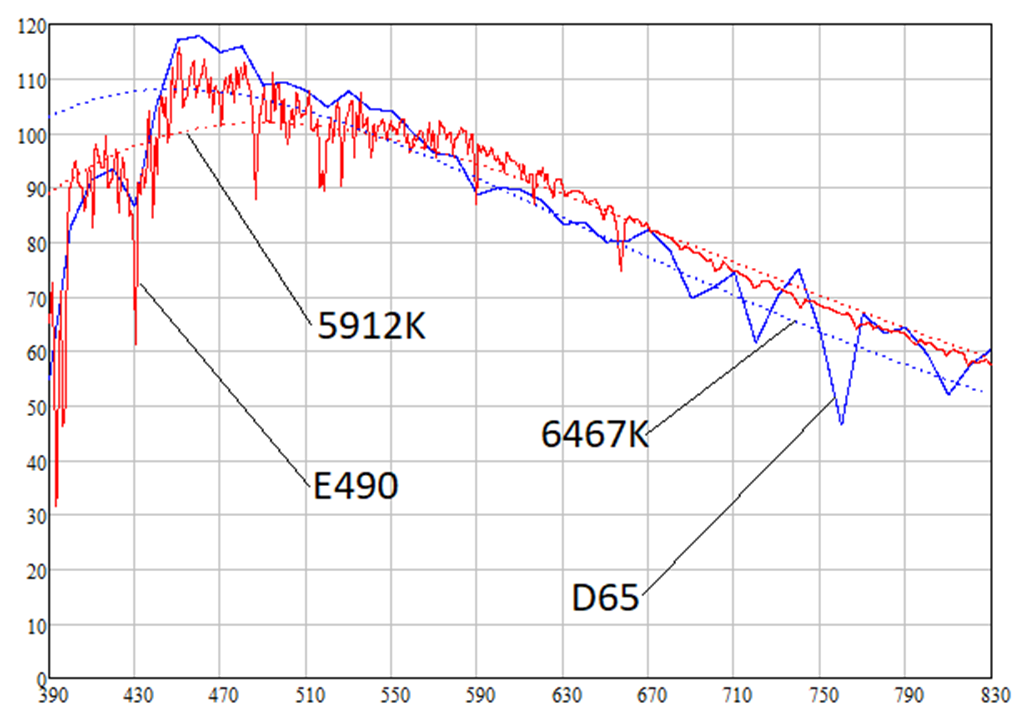
On peut noter que la densité spectrale du rayonnement solaire est supérieure à celle d'une source de lumière blanche à des longueurs d'onde plus longues, c'est-à-dire à des longueurs d'onde de lumière rouge (620-770 nm). Cela signifie que le soleil a une teinte rougeâtre. En effet, les calculs donnent les couleurs suivantes des sources lumineuses D65, E490 et des corps absolument noirs des températures correspondantes (comme je l'ai dit, du papier blanc avec un albédo de 0,91 est considéré):



Veuillez noter que les coordonnées sRGB du Soleil et la température absolue du corps noir 5912K coïncident exactement. Cela ne s'explique par rien, cela arrive juste.

La couleur des cercles dans la dernière image est la vraie couleur du Soleil depuis l'espace. L'œil humain voit clairement la teinte rougeâtre du soleil. Donc, le fait que le Soleil de l'espace soit blanc est un grand mythe! Il convient de noter que pour une raison quelconque, cette nuance n'est pas observée dans les photographies et la vidéo du programme Apollo. Sur ces photographies, la teinte rougeâtre visible du Soleil apparaîtrait certainement sur les surfaces blanches du drapeau américain et des combinaisons spatiales. Et comme cela sera montré ci-dessous, cette nuance du Soleil contribue de façon notable à la "rougeur" ​​de la Lune depuis l'espace.

La lune est-elle différente ou de même couleur?

Les opposants à la théorie de la conspiration lunaire font la promotion de la version selon laquelle la lune est de couleur différente. Apparemment, par endroits, la lune est grise, par endroits, elle est brune, et en même temps, l'Apollon a atterri là où la lune est grise. Mais cette version contredit directement les données scientifiques. L'article [ 7 ] dit explicitement:

Les différences de couleur sur la lune sont extrêmement faibles.

Shevchenko écrit également dans son livre [ 8 ]:

Pendant de nombreuses années, le célèbre chercheur américain T. McCord a travaillé dans ce sens.Il a obtenu plus de 200 spectres pour différentes sections de la surface lunaire de 10 à 20 km chacune. Toutes les courbes obtenues sont fondamentalement similaires en apparence.

Donc, non, la lune n'est pas de couleur différente, mais la même.

Données de couleur de la lune selon Shevchenko

Shevchenko dans son livre [ 8 ] donne la dépendance suivante de la réflectivité sur la longueur d'onde.



Dans mes calculs, j'utilise une interpolation linéaire par morceaux de ces données. J'ai reçu les données manquantes dans la gamme de 820–830 nm par suite directe du segment dans la gamme de 690–820 nm.

Données de couleur de lune par LRO

La dépendance de la réflectivité de la surface lunaire sur les conditions d'éclairage et d'observation à des longueurs d'onde de 321 nm à 689 nm est donnée dans [ 9 ]. Les paramètres du modèle ont été calculés sur la base de l'analyse des données obtenues par le Lunar Reconnaissance Orbiter (en abrégé LRO). Les conditions d'éclairage et d'observation sont déterminées par trois paramètres i (angle d'incidence), e (angle de réflexion) et g (angle de phase). Ces angles sont représentés dans le diagramme suivant:



L'angle de phase peut être exprimé en termes d'angle azimutal$$Ψ en utilisant lethéorème de cosinus sphériquecomme suit:$\varPsi$

$$

$$g=\arccos\left(\cos\left(i\right)\cos\left(e\right)+\sin\left(i\right)\sin\left(e\right)\cos\left(\varPsi\right)\right)$$

Dans les calculs, je prends les valeurs traditionnelles des angles i = g = 30 °, e = 0 °. Pour de tels angles, la dépendance suivante de la réflectance sur la longueur d'onde est obtenue (graphique lro30):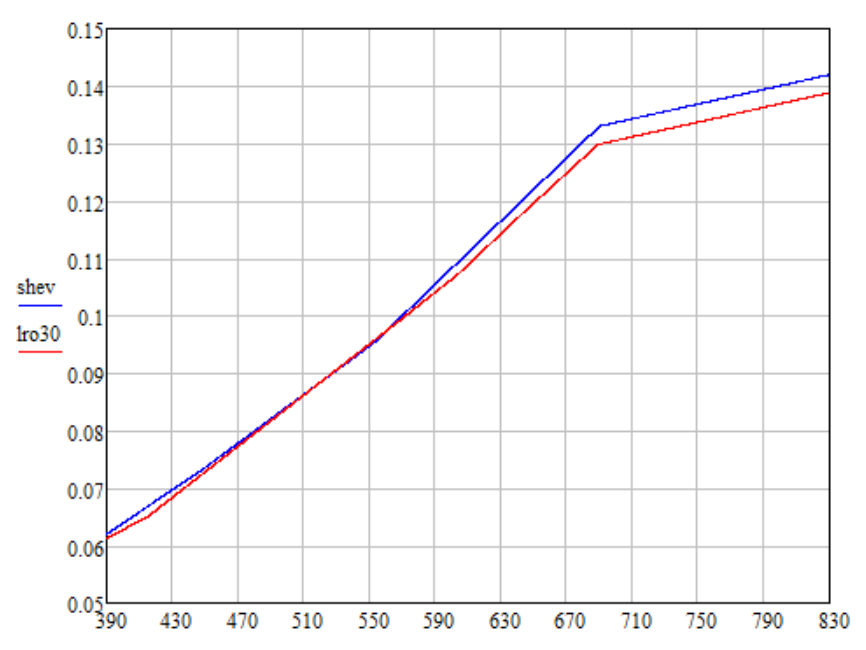


J'ai fait une extrapolation linéaire des données LRO à l'intervalle 689-830 nm afin que le rapport des valeurs aux points 830 nm et 689 nm soit le même que les données de Shevchenko ( calendrier shev). J'ai également renormalisé les données de Shevchenko en multipliant par 0,8315 afin que la luminosité des calculs de couleurs résultants selon Shevchenko et LRO soit la même.

Informations de couleur pour la lune par Kaguya

L'ouvrage [ 10 ] présente des données obtenues par le deuxième satellite lunaire artificiel japonais. Malheureusement, la réflectivité dans la gamme de longueurs d'onde visibles est donnée avec une très faible résolution, donc je ne l'utilise pas dans mes calculs.

Mais le travail est intéressant en ce qu'il parle des divergences colossales des données de Kaguya avec les données de la mission Apollo 16. Et c'est l'un des rares cas où la communauté scientifique parle ouvertement d'incohérences associées aux vols des Américains vers la lune.

Résultats des calculs

De plus, j'utiliserai la notation suivante:
D65 - une source standard de lumière blanche D65;
E490 - source de lumière du soleil en l'absence d'atmosphère;
B-0.91 - papier blanc avec un albédo de 0,91;
LRO (30 °) - Données LRO pour les angles traditionnels i = g = 30 °, e = 0 °;
Shevch. - données sur Shevchenko;
ling. (2 °) - coordonnées RVB linéaires dans un champ de vision de 2 degrés ;
ling. (10 °) - coordonnées RVB linéaires dans un champ de vision de 10 degrés ;
ling. (moyenne) - coordonnées RVB linéaires moyennées surChamp de vision de 2 degrés et 10 degrés ;
sRGB (100%) - coordonnées sRGB obtenues à partir de coordonnées RVB linéaires moyennées sur un champ de vision de 2 degrés et 10 degrés ;
sRGB (200%) - coordonnées sRGB obtenues à partir de coordonnées RVB linéaires doublées moyennées sur un champ de vision de 2 degrés et 10 degrés ;
sRGB (300%) - coordonnées sRGB obtenues à partir de coordonnées RVB linéaires triplées moyennées sur un champ de vision de 2 degrés et 10 degrés ;
sRGB (400%) - Coordonnées sRGB obtenues à partir de quadruples coordonnées RVB linéaires moyennées surChamp de vision de 2 degrés et 10 degrés ;
col. rythme. - température de couleur obtenue à partir de coordonnées RVB linéaires moyennes sur un champ de vision de 2 degrés et 10 degrés ;

D65

	B-0.91	LRO (30 °)	Shevch.
ling. (2 °)	0.9076,0.9120,0.8968	0.1177,0.0931,0.0688	0.1202,0.0931,0.0697
ling. (10 °)	0.9084,0.9122,0.8929	0.1165.0.0916.0.0687	0.1188,0.0917,0.0696
ling. (moyenne)	0,9080,0,9121,0,8948	0.1171,0.0924,0.0688	0.1195,0.0924,0.0697
sRGB (100%)	rgb (244.245.243)	rgb (96.86.74)	rgb (97.86.75)
sRGB (200%)	-	rgb (133.119.104)	rgb (134.119.104)
sRGB (300%)	-	rgb (160.144.125)	rgb (161.144.126)
sRGB (400%)	-	rgb (182.164.143)	rgb (184.164.144)
col. rythme.	6467K	4928K	4891K

E490

	B-0.91	LRO (30 °)	Shevch.
ling. (2 °)	1.0005,0.8892,0.8490	0.1283.0.0909.0.0649	0.1310,0.0909,0.0657
ling. (10 °)	1.0021,0.8888,0.8483	0.1272,0.0895,0.0650	0.1297,0.0895,0.0659
. (.)	1.0013,0.8890,0.8486	0.1277,0.0902,0.0649	0.1303,0.0902,0.0658
sRGB (100%)	rgb(255,242,237)	rgb(100,85,72)	rgb(101,85,73)
sRGB (200%)	-	rgb(138,118,101)	rgb(140,118,102)
sRGB (300%)	-	rgb(166,142,122)	rgb(168,142,123)
sRGB (400%)	-	rgb(189,162,139)	rgb(191,162,140)
. .	5912K	4550K	4512K

L'image suivante montre les couleurs de surface lunaire sRGB (100%) , sRGB (200%) (double luminosité), sRGB (300%) (triple luminosité), sRGB (400%) (luminosité quadruple) avec une source de lumière E490 (c.-à-d. après observation depuis l'espace) selon les données de LRO et Shevchenko.



Comme vous pouvez le voir, la Lune de l'espace a une couleur brune selon LRO et Shevchenko. Par Shevchenko, il s'avère un peu (à peine perceptible) plus rouge que par LRO.

Couleur de la lune en photos

Dans cette section, nous traiterons de la coloration des photographies. Laissez l'image img et la couleur en coordonnées linéaires de RGB être données. Chaque pixel d'image est remplacé par un pixel d'une couleur donnée de la même luminosité que celle de la couleur du pixel d'origine. L'image dans Mathcad est présentée comme une matrice de coordonnées sRGB unique, qui est obtenue en cousant les trois matrices «R», «G», «B» de gauche à droite. Dans cet esprit, la procédure de coloration est la suivante:

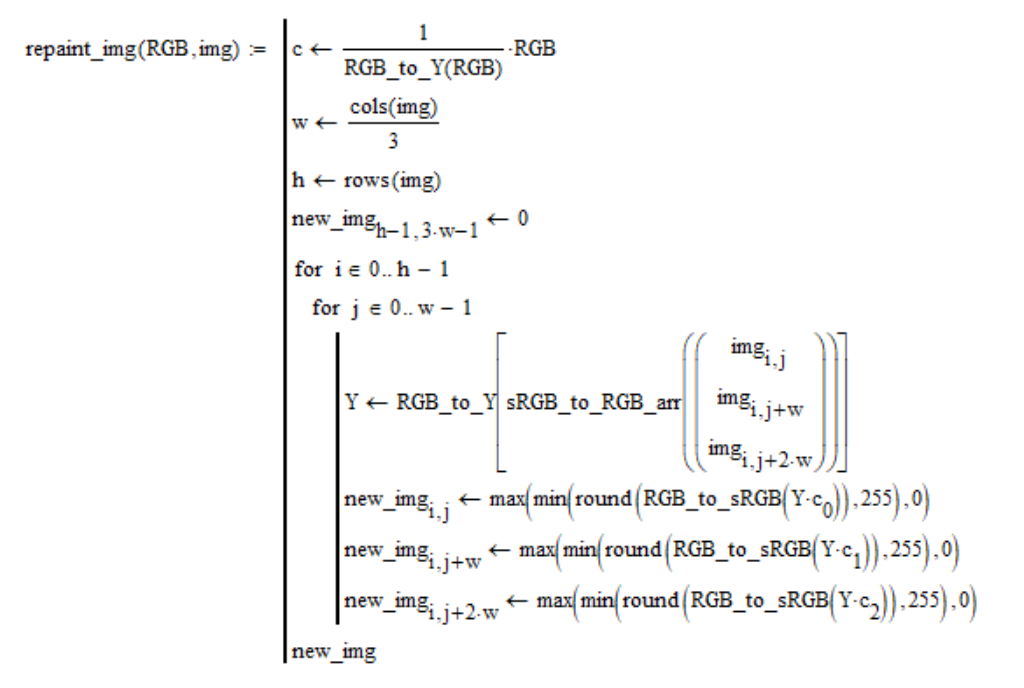
Par intérêt, j'ai pris des photos de la surface lunaire des albums photos du programme américain Apollo et l'ai repeinte dans les couleurs obtenues à partir de mes calculs. Je ne donne que les résultats et je conclus moi-même si ces photos sont vraies ou fausses.

Le résultat de la coloration de la photo AS11-44-6552 :



Au milieu, les photos originales. À gauche, les photographies sont colorées selon les données LRO pour les angles traditionnels i = g = 30 ° , e = 0 ° , et à droite, selon les données de Shevchenko. La rangée supérieure correspond à la source de lumière standard D65, c'est-à-dire que la rangée supérieure montre les couleurs de surface de la lune, qui auraient été obtenues si le soleil avait été blanc. La rangée inférieure correspond à la source de lumière E490, c'est-à-dire que la rangée inférieure montre les couleurs naturelles de la surface de la lune lorsqu'elle est observée depuis l'espace.

Comme vous pouvez le voir, la teinte rougeâtre du Soleil contribue de façon notable à la «rougeur» de la surface de la Lune, qui à la fin semble brune, pas grise du tout.

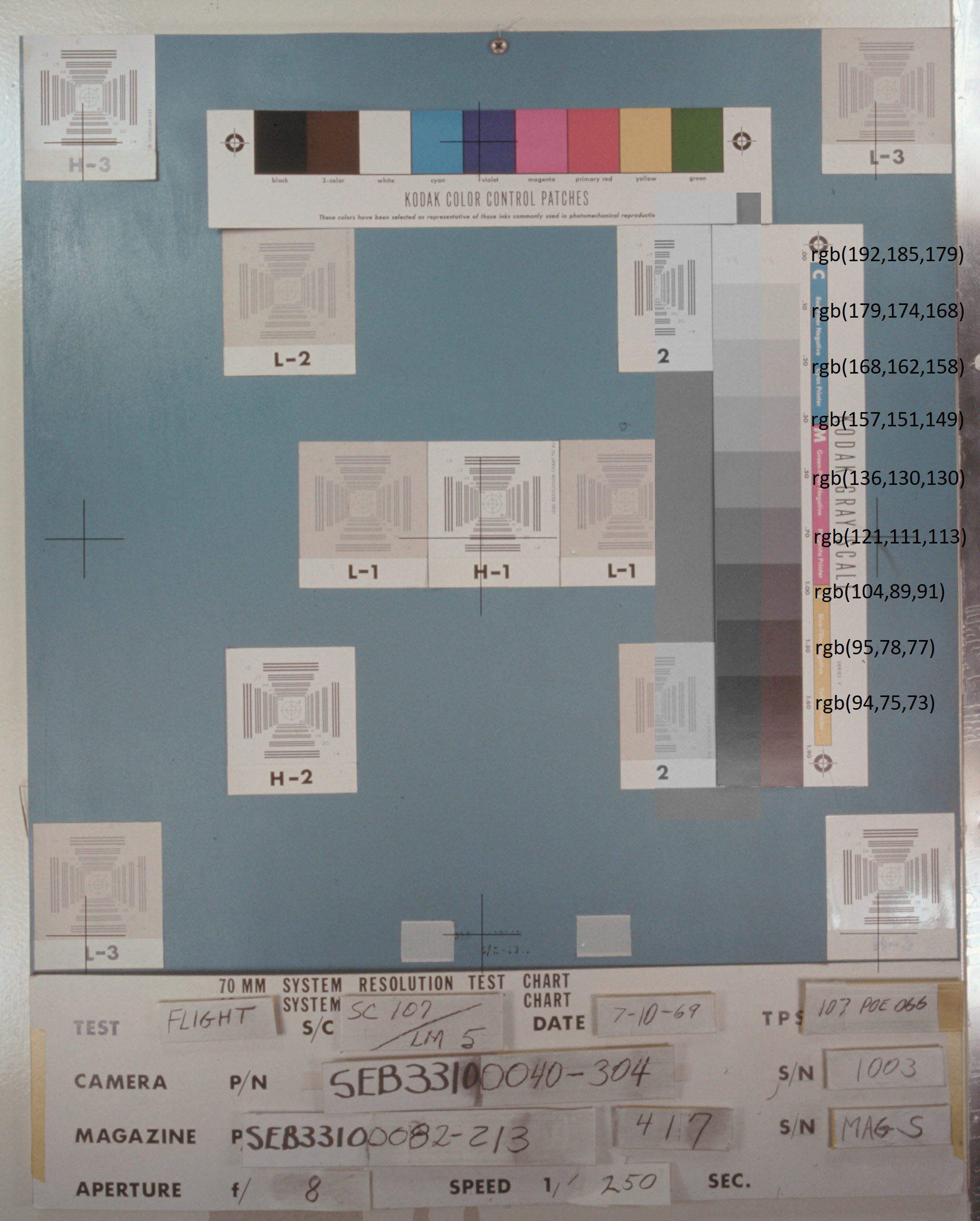
La couleur grise de la Lune sur les photographies de la NASA pourrait s'expliquer par le fait que le film "est devenu" bleu pour une raison quelconque, mais cette version disparaît immédiatement si nous analysons les images de dégradés de gris à la fin des albums. La photo as11-44-graphique montre une telle image pour la dernière photo ci-dessus. J'ai laissé de vrais gris de la même luminosité à gauche des dégradés de gris dans la même luminosité que sur la photo, et j'ai également noté les coordonnées sRGB. Le résultat est l'image suivante:



Comme vous pouvez le voir, le film est non seulement «passé» au bleu, mais même «parti» un peu dans la direction opposée au bleu. Une telle déviation ne peut pas devenir brune en grise.

Le résultat de la coloration de la photo AS11-40-5903 :



Sur la photo originale, la surface lunaire par endroits n'a pas seulement une couleur grise, mais même une légère teinte bleuâtre. La photo du graphique as11-40 montre l'image de gradation de gris correspondante:



Le film n'est pas "parti" dans la couleur "bleue", mais dans la "rouge". Et même après cela, pour une raison quelconque, la surface lunaire sur la photographie de la NASA est grise.

Le résultat de la coloration de la photo AS11-37-5455 :



C'est l'une des rares photographies du programme Apollo, où la surface lunaire a une teinte brune, bien que pas entièrement. Les opposants à la théorie du complot lunaire adorent le montrer, disent-ils, regardez, le brun est le même. Mais ici, la capture s'est glissée. Analysons la photo sous forme de graphique 11-37 , qui montre l'image correspondante des dégradés de gris:



Le film est simplement «devenu» brun. C'est toute la raison de la teinte brune de la surface lunaire sur les photographies de la NASA.

La dépendance de la couleur de la surface lunaire des conditions d'éclairage et d'observation

En utilisant les données LRO données dans [ 9 ] , nous étudions comment la couleur de la surface lunaire change en raison des conditions d'éclairage et d'observation. Considérons la source de lumière E490 (le Soleil depuis l'espace) et les différentes valeurs des angles i , e , $$$\ varPsi$ . L'image suivante montre le résultat, où les couleurs de la rangée supérieure sont trois fois plus lumineuses et les couleurs de la rangée inférieure sont réduites à la même luminosité Y = 0,5 .



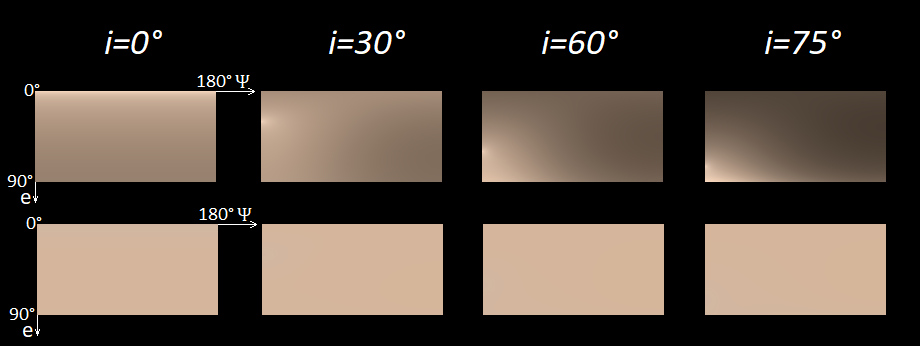
Comme vous pouvez le voir sur l'image, seule la luminosité change. Dans la rangée du bas, les couleurs sont presque les mêmes partout pour l'œil humain. Bien que, si vous regardez de près, dans le cas i = 0 °, vous pouvez voir une très faible déviation vers le côté gris lorsque e s'approche de zéro.

La couleur du sol lunaire

Il y a une photographie très étrange sur le site Web de la NASA, à savoir cette photographie de l' échantillon de sol lunaire n ° 10005 .



Le sol lunaire sur la photo semble brun, même trop brun, étant donné que l'éclairage a été produit par une source de lumière blanche. La balance des blancs correcte peut être vérifiée par la couleur du papier blanc tombé dans le cadre.

Peut-être que c'est le même sol orange que les astronautes d'Apollo 17 ont découvert? Non! Le document [ 11 ] indiquait clairement que l'échantillon avait été prélevé par des astronautes d'Apollo 11.

Écoutons maintenant ce que Neil Armstrong (astronaute d'Apollo 11) dit dans une interview avec Patrick Moore [ 12 ] , qu'il a donnée en 1970.

Lorsque vous regardez le sol près ou dans votre main, vous constatez qu'il est en fait gris charbon, et nous n'avons surtout rien trouvé de différent de cette couleur.

(Lorsque vous regardez le matériau de près, comme si dans votre main, vous trouvez que c'est un gris anthracite en fait, et nous n'avons jamais pu trouver des choses très différentes de cette couleur.)

Il se trouve, Neil Armstrong, je n'ai pas peur du mot, a menti.

Littérature

1. Color & Vision Research Laboratory - Nouvelles fonctions CIE XYZ transformées à partir des fonctions CIE (2006) LMS
2. International Color Consortium - Un espace couleur standard par défaut pour Internet: sRGB
3. Recommandation UIT-RBT.709 - Valeurs des paramètres des normes TVHD pour la production et l'échange international de programmes
4. Robertson R. «Calcul de la température de couleur et de la température de distribution corrélées» / .Opt. Soc. Am.58, 1528 (1968).
5. 2000 ASTM Standard Extraterrestrial Spectrum Reference E-490-00
6. Illuminant standard CIE D65
7. «Les premiers résultats de la détermination des propriétés physico-mécaniques des sols de la Lune», Moscou: 1970. Gosstroy de l'URSS, éd. prof. Dr. tech. Sciences de V.G. Bulychev, p. 8.
8. Shevchenko V.V., Moon and its observation, 1983, p. 91-92.
9. Hapke, B., B. Denevi, H. Sato, S. Braden et M. Robinson (2012), La dépendance de la longueur d'onde de la courbe de phase lunaire vue par la caméra grand angle Lunar Reconnaissance Orbiter, J. Geophys. Rés., 117, E00H15
10. Ohtake, M. et al. (2010), Deriving the Absolute Reflectance of Lunar Surface Using SELENE (Kaguya) Multiband Imager Data, Space Sci. Rév., 154, 57-77
11. THE APOLLO 11 DRIVE TUBES, Dissection and description by Judith H. Allton, NASA (1978)
12. BBC Entretien de Neil Armstrong avec Patrick Moore (1970)