Gros o

Remarque Traduction abrégée, plutôt raconter avec vos propres mots.
UPD: comme indiqué dans les commentaires, les exemples ne sont pas parfaits. L'auteur ne cherche pas la meilleure solution au problème, son but est d'expliquer la complexité des algorithmes «sur les doigts».

La notation Big O est nécessaire pour décrire la complexité des algorithmes. Pour cela, le concept de temps est utilisé. Le sujet est effrayant pour beaucoup, les programmeurs évitant de parler du "temps de l'ordre N" est une chose courante.

Si vous êtes en mesure d'évaluer le code en termes de Big O, vous êtes probablement considéré comme un «gars intelligent». Et très probablement, vous passerez par votre prochaine entrevue. Vous ne serez pas arrêté par la question de savoir s'il est possible de réduire la complexité d'un morceau de code à n log n contre n ^ 2.

Structures de données

Le choix de la structure des données dépend de la tâche spécifique: du type de données et de l'algorithme pour leur traitement. Diverses structures de données (en .NET ou Java ou Elixir) ont été créées pour certains types d'algorithmes.

Souvent, en choisissant l'une ou l'autre structure, nous copions simplement la solution généralement acceptée. Dans la plupart des cas, cela suffit. Mais en fait, sans comprendre la complexité des algorithmes, nous ne pouvons pas faire un choix éclairé. Le sujet des structures de données ne peut être passé qu'après la complexité des algorithmes.

Ici, nous n'utiliserons que des tableaux de nombres (comme dans une interview). Exemples JavaScript.

Commençons par le plus simple: O (1)

Prenez un tableau de 5 nombres:

const nums = [1,2,3,4,5]; 

Supposons que vous ayez besoin d'obtenir le premier élément. Pour cela, nous utilisons l'index:

 const nums = [1,2,3,4,5]; const firstNumber = nums[0]; 

À quel point cet algorithme est-il compliqué? Nous pouvons dire: "pas du tout compliqué - prenez simplement le premier élément du tableau." C'est vrai, mais il est plus correct de décrire la complexité à travers le nombre d'opérations effectuées pour atteindre le résultat, selon l'entrée ( opérations d' entrée).

En d'autres termes: combien d'opérations augmenteront à mesure que le nombre de paramètres d'entrée augmentera.

Dans notre exemple, il y a 5 paramètres d'entrée, car il y a 5 éléments dans le tableau. Pour obtenir le résultat, vous devez effectuer une opération (prendre un élément par index). Combien d'opérations seront nécessaires s'il y a 100 éléments dans le tableau? Ou 1000? Ou 100 000? Néanmoins, une seule opération est nécessaire.

C'est-à-dire: «une opération pour toutes les données d'entrée possibles» - O (1).

O (1) peut être lu comme «complexité d'ordre 1» (ordre 1) ou «algorithme s'exécute en temps constant / constant» (temps constant).

Vous avez déjà deviné que les algorithmes O (1) sont les plus efficaces.

Itérations et "heure de l'ordre n": O (n)

Maintenant, trouvons la somme des éléments du tableau:

 const nums = [1,2,3,4,5]; let sum = 0; for(let num of nums){ sum += num; } 

Encore une fois, nous nous demandons: de combien d'opérations d'entrée avons-nous besoin? Ici, vous devez trier tous les éléments, c'est-à-dire opération sur chaque élément. Plus le tableau est grand, plus il y a d'opérations.

Utilisation de la notation Big O: O (n), ou «complexité de l'ordre n (ordre n)». De plus, ce type d'algorithme est appelé «linéaire» ou que l'algorithme est «mis à l'échelle linéairement».

Analyse

Pouvons-nous rendre la sommation plus efficace? Généralement non. Et si nous savons que le tableau est garanti pour commencer à 1, trié et qu'il n'y a pas d'espace? Ensuite, nous pouvons appliquer la formule S = n (n + 1) / 2 (où n est le dernier élément du tableau):

 const sumContiguousArray = function(ary){ //get the last item const lastItem = ary[ary.length - 1]; //Gauss's trick return lastItem * (lastItem + 1) / 2; } const nums = [1,2,3,4,5]; const sumOfArray = sumContiguousArray(nums); 

Un tel algorithme est beaucoup plus efficace que O (n), de plus, il est exécuté en «temps constant / constant», c'est-à-dire c'est O (1).

En fait, il y a plus d'une opération: vous devez obtenir la longueur du tableau, obtenir le dernier élément, effectuer la multiplication et la division. N'est-ce pas O (3) ou quelque chose? En notation Big O, le nombre réel d'étapes n'est pas important, il est important que l'algorithme s'exécute en temps constant.

Les algorithmes à temps constant sont toujours O (1). La même chose avec les algorithmes linéaires, en fait, les opérations peuvent être O (n + 5), dans Big O la notation est O (n).

Pas les meilleures solutions: O (n ^ 2)

Écrivons une fonction qui vérifie le tableau pour les doublons. Solution de boucle imbriquée:

 const hasDuplicates = function (num) { //loop the list, our O(n) op for (let i = 0; i < nums.length; i++) { const thisNum = nums[i]; //loop the list again, the O(n^2) op for (let j = 0; j < nums.length; j++) { //make sure we're not checking same number if (j !== i) { const otherNum = nums[j]; //if there's an equal value, return if (otherNum === thisNum) return true; } } } //if we're here, no dups return false; } const nums = [1, 2, 3, 4, 5, 5]; hasDuplicates(nums);//true 

Nous savons déjà que l'itération du tableau est O (n). Nous avons une boucle imbriquée, pour chaque élément, nous réitérons - c'est-à-dire O (n ^ 2) ou «complexité d'ordre n carré».

Les algorithmes avec des boucles imbriquées sur la même collection sont toujours O (n ^ 2).

"La complexité de l'ordre du log n": O (log n)

Dans l'exemple ci-dessus, une boucle imbriquée, par elle-même (si vous ne prenez pas en compte qu'elle est imbriquée), a une complexité O (n), car c'est l'énumération des éléments du tableau. Ce cycle se termine dès que l'élément souhaité est trouvé, c'est-à-dire en fait, tous les éléments ne seront pas énumérés. Mais la notation Big O considère toujours le pire des cas - l'élément que vous recherchez peut être le dernier.

Ici, une boucle imbriquée est utilisée pour rechercher un élément donné dans un tableau. La recherche d'un élément dans un tableau, dans certaines conditions, peut être optimisée - mieux que O (n) linéaire.

Laissez le tableau être trié. Ensuite, nous pouvons utiliser l'algorithme de recherche binaire: diviser le tableau en deux moitiés, éliminer les inutiles, diviser à nouveau le reste en deux parties, et ainsi de suite jusqu'à ce que nous trouvions la valeur souhaitée. Ce type d'algorithme est appelé diviser et conquérir Diviser et conquérir.



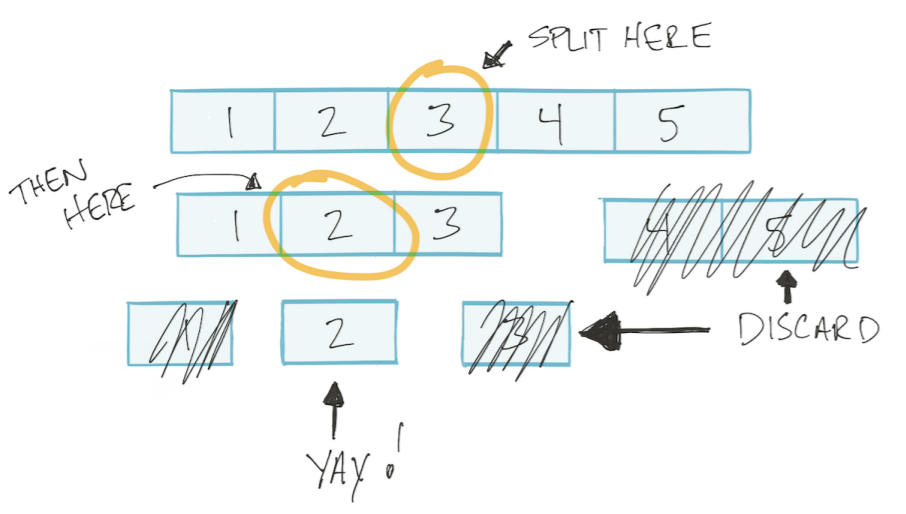
Cet algorithme est basé sur un logarithme.

Aperçu rapide des logarithmes

Prenons un exemple, à quoi x sera-t-il égal?

x ^ 3 = 8

Nous devons prendre la racine cubique de 8 - ce sera 2. Maintenant, plus difficile

2 ^ x = 512

En utilisant le logarithme, le problème peut être écrit comme

log2 (512) = x

"Le logarithme en base 2 de 512 est x." Faites attention à la «base 2», c'est-à-dire nous pensons par deux - combien de fois vous devez multiplier 2 pour obtenir 512.

Dans l'algorithme de recherche binaire, à chaque étape, nous divisons le tableau en deux parties.

Mon ajout. C'est-à-dire dans le pire des cas, nous faisons autant d'opérations que nous pouvons diviser le tableau en deux parties. Par exemple, combien de fois pouvons-nous diviser un tableau de 4 éléments en deux parties? 2 fois. Et un tableau de 8 éléments? 3 fois. C'est-à-dire nombre de divisions / opérations = log2 (n) (où n est le nombre d'éléments dans le tableau).

Il s'avère que la dépendance du nombre d'opérations sur le nombre d'éléments d'entrée est décrite comme log2 (n)


Ainsi, en utilisant la notation Big O, l'algorithme de recherche binaire a la complexité O (log n).

Améliorez O (n ^ 2) en O (n log n)

Revenons à la tâche de vérification du tableau pour les doublons. Nous avons itéré sur tous les éléments du tableau, et pour chaque élément, nous avons à nouveau itéré. Ils ont fait O (n) à l'intérieur de O (n), c'est-à-dire O (n * n) ou O (n ^ 2).

Nous pouvons remplacer la boucle imbriquée par une recherche binaire *. C'est-à-dire il suffit de passer par tous les éléments de O (n), à l'intérieur on fait O (log n). Il s'avère O (n * log n), ou O (n log n).

 const nums = [1, 2, 3, 4, 5]; const searchFor = function (items, num) { //use binary search! //if found, return the number. Otherwise... //return null. We'll do this in a later chapter. } const hasDuplicates = function (nums) { for (let num of nums) { //let's go through the list again and have a look //at all the other numbers so we can compare if (searchFor(nums, num)) { return true; } } //only arrive here if there are no dups return false; } 

* ATTENTION, afin d'éviter l' impression . L'utilisation de la recherche binaire pour vérifier un tableau pour les doublons est une mauvaise solution. Il montre uniquement comment, en termes Big O, évaluer la complexité de l'algorithme indiqué dans la liste de codes ci-dessus. Un bon algorithme ou un mauvais n'est pas important pour cet article; la visibilité est importante.

Penser en termes de Big O

• L'obtention de l'élément de collection est O (1). Que ce soit par index dans un tableau ou par clé dans un dictionnaire en notation Big O, ce sera O (1)
• Itérer sur une collection est O (n)
• Les boucles imbriquées sur la même collection sont O (n ^ 2)
• Diviser et conquérir toujours O (log n)
• Les itérations qui utilisent Divide and Conquer sont O (n log n)