Dans les articles précédents, nous avons discuté du moteur d'indexation PostgreSQL, de l'interface des méthodes d'accès et de deux méthodes d'accès: l' index de hachage et l' arborescence B. Dans cet article, nous décrirons les index GiST.

Gist

GiST est l'abréviation de "arbre de recherche généralisé". Il s'agit d'un arbre de recherche équilibré, tout comme "l'arbre b" discuté précédemment.

Quelle est la différence? L'index "Btree" est strictement lié à la sémantique de comparaison: la prise en charge des opérateurs "supérieur", "moins" et "égal" est tout ce dont il est capable (mais très capable!) Cependant, les bases de données modernes stockent les types de données pour lesquels ces opérateurs n'a aucun sens: géodonnées, documents texte, images, ...

La méthode d'indexation GiST vient à notre aide pour ces types de données. Il permet de définir une règle pour distribuer des données de type arbitraire à travers un arbre équilibré et une méthode pour utiliser cette représentation pour l'accès par un opérateur. Par exemple, l'index GiST peut "accueillir" l'arbre R pour les données spatiales avec prise en charge des opérateurs de position relative (situés à gauche, à droite, contient, etc.) ou l'arbre RD pour les ensembles prenant en charge les opérateurs d'intersection ou d'inclusion.

Grâce à l'extensibilité, une méthode totalement nouvelle peut être créée à partir de zéro dans PostgreSQL: à cette fin, une interface avec le moteur d'indexation doit être implémentée. Mais cela nécessite non seulement la préméditation de la logique d'indexation, mais également le mappage des structures de données aux pages, la mise en œuvre efficace des verrous et la prise en charge d'un journal d'écriture anticipée. Tout cela suppose de hautes compétences de développeur et un gros effort humain. GiST simplifie la tâche en prenant en charge les problèmes de bas niveau et en offrant sa propre interface: plusieurs fonctions relatives non pas aux techniques, mais au domaine d'application. En ce sens, nous pouvons considérer GiST comme un cadre pour la construction de nouvelles méthodes d'accès.

La structure

GiST est un arbre à hauteur équilibrée composé de pages de nœuds. Les nœuds sont constitués de lignes d'index.

Chaque ligne d'un nœud feuille (ligne feuille), en général, contient un prédicat (expression booléenne) et une référence à une ligne de table (TID). Les données indexées (clé) doivent respecter ce prédicat.

Chaque ligne d'un nœud interne (ligne interne) contient également un prédicat et une référence à un nœud enfant, et toutes les données indexées du sous-arbre enfant doivent respecter ce prédicat. En d'autres termes, le prédicat d'une ligne interne inclut les prédicats de toutes les lignes enfants. Ce trait important de l'index GiST remplace l'ordre simple de l'arbre B.

La recherche dans l'arborescence GiST utilise une fonction de cohérence spécialisée ("cohérente") - l'une des fonctions définies par l'interface et implémentée à sa manière pour chaque famille d'opérateurs prise en charge.

La fonction de cohérence est appelée pour une ligne d'index et détermine si le prédicat de cette ligne est cohérent avec le prédicat de recherche (spécifié comme " expression d'opérateur de champ indexé "). Pour une ligne interne, cette fonction détermine en fait s'il faut descendre jusqu'au sous-arbre correspondant, et pour une ligne feuille, la fonction détermine si les données indexées répondent au prédicat.

La recherche commence par un nœud racine, comme une recherche d'arbre normale. La fonction de cohérence permet de savoir dans quels nœuds enfants il est logique d'entrer (il peut y en avoir plusieurs) et lesquels non. L'algorithme est ensuite répété pour chaque nœud enfant trouvé. Et si le nœud est feuille, la ligne sélectionnée par la fonction de cohérence est renvoyée comme l'un des résultats.

La recherche est la profondeur d'abord: l'algorithme essaie d'abord d'atteindre un nœud feuille. Cela permet de renvoyer les premiers résultats dès que possible (ce qui peut être important si l'utilisateur n'est intéressé que par plusieurs résultats plutôt que par tous).

Notons une fois de plus que la fonction de cohérence n'a rien à voir avec les opérateurs "supérieurs", "inférieurs" ou "égaux". La sémantique de la fonction de cohérence peut être très différente et, par conséquent, l'indice n'est pas supposé renvoyer des valeurs dans un certain ordre.

Nous ne discuterons pas des algorithmes d'insertion et de suppression de valeurs dans GiST: quelques fonctions d'interface supplémentaires effectuent ces opérations. Il y a cependant un point important. Lorsqu'une nouvelle valeur est insérée dans l'index, la position de cette valeur dans l'arborescence est sélectionnée de sorte que les prédicats de ses lignes parentes soient étendus le moins possible (idéalement, pas du tout étendus). Mais lorsqu'une valeur est supprimée, le prédicat de la ligne parent n'est plus réduit. Cela ne se produit que dans des cas comme ceux-ci: une page est divisée en deux (lorsque la page n'a pas assez d'espace pour l'insertion d'une nouvelle ligne d'index) ou l'index est recréé à partir de zéro (avec la commande REINDEX ou VACUUM FULL). Par conséquent, l'efficacité de l'index GiST pour les données changeant fréquemment peut se dégrader avec le temps.

De plus, nous considérerons quelques exemples d'index pour divers types de données et propriétés utiles de GiST:

• Points (et autres entités géométriques) et recherche des voisins les plus proches.
• Intervalles et contraintes d'exclusion.
• Recherche plein texte.

Arbre R pour les points

Nous allons illustrer ce qui précède par l'exemple d'un index pour les points dans un plan (nous pouvons également construire des index similaires pour d'autres entités géométriques). Un arbre B standard ne convient pas à ce type de données car aucun opérateur de comparaison n'est défini pour les points.

L'idée de R-tree est de diviser le plan en rectangles qui couvrent au total tous les points indexés. Une ligne d'index stocke un rectangle, et le prédicat peut être défini comme ceci: "le point recherché se trouve dans le rectangle donné".

La racine de l'arbre R contiendra plusieurs grands rectangles (pouvant se croiser). Les nœuds enfants contiendront des rectangles de plus petite taille qui sont intégrés dans le parent et couvrent au total tous les points sous-jacents.

En théorie, les nœuds terminaux doivent contenir des points indexés, mais le type de données doit être le même dans toutes les lignes d'index et, par conséquent, les rectangles sont à nouveau stockés, mais «réduits» en points.

Pour visualiser une telle structure, nous fournissons des images pour trois niveaux de l'arborescence R. Les points sont les coordonnées des aéroports (similaires à celles du tableau "aéroports" de la base de données de démonstration , mais davantage de données sur openflights.org sont fournies).


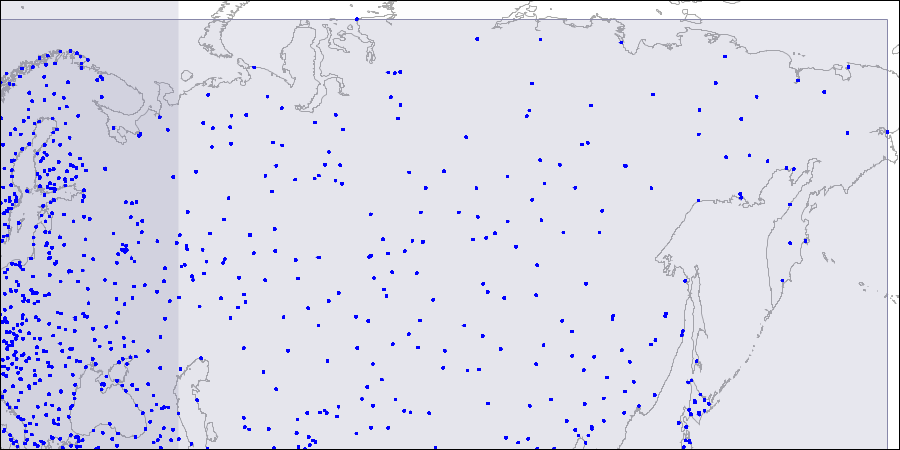Niveau un: deux grands rectangles se croisant sont visibles.


Niveau deux: les grands rectangles sont divisés en zones plus petites.


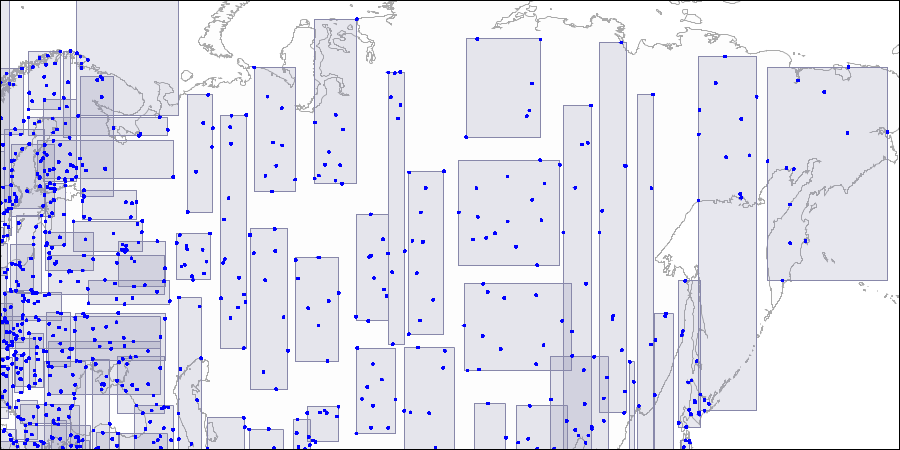Niveau trois: chaque rectangle contient autant de points que pour tenir une page d'index.

Considérons maintenant un exemple très simple "à un niveau":

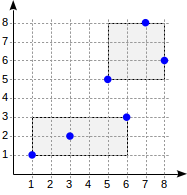
postgres=# create table points(p point); postgres=# insert into points(p) values (point '(1,1)'), (point '(3,2)'), (point '(6,3)'), (point '(5,5)'), (point '(7,8)'), (point '(8,6)'); postgres=# create index on points using gist(p); 

Avec ce fractionnement, la structure de l'index se présentera comme suit:



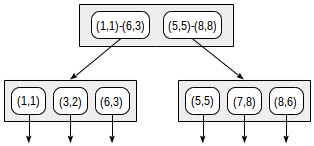
L'index créé peut être utilisé pour accélérer la requête suivante, par exemple: "trouver tous les points contenus dans le rectangle donné". Cette condition peut être formalisée comme suit: p <@ box '(2,1),(6,3)' (opérateur <@ de la famille "points_ops" signifie "contenu dans"):

 postgres=# set enable_seqscan = off; postgres=# explain(costs off) select * from points where p <@ box '(2,1),(7,4)'; 

  QUERY PLAN ---------------------------------------------- Index Only Scan using points_p_idx on points Index Cond: (p <@ '(7,4),(2,1)'::box) (2 rows) 

La fonction de cohérence de l'opérateur (" indexed-field <@ expression ", où indexed-field est un point et l' expression est un rectangle) est définie comme suit. Pour une ligne interne, elle renvoie «oui» si son rectangle coupe le rectangle défini par l' expression . Pour une ligne feuille, la fonction renvoie "oui" si son point (rectangle "réduit") est contenu dans le rectangle défini par l'expression.



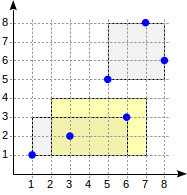
La recherche commence par le nœud racine. Le rectangle (2,1) - (7,4) coupe avec (1,1) - (6,3), mais ne coupe pas avec (5,5) - (8,8), par conséquent, il n'y a pas besoin pour descendre au deuxième sous-arbre.



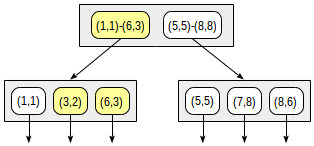
En atteignant un nœud feuille, nous passons par les trois points qui y sont contenus et retournons deux d'entre eux comme résultat: (3.2) et (6.3).

 postgres=# select * from points where p <@ box '(2,1),(7,4)'; 

  p ------- (3,2) (6,3) (2 rows) 

Internes

Malheureusement, le "pageinspect" habituel ne permet pas d'examiner l'index GiST. Mais une autre voie est disponible: l'extension "gevel". Il n'est pas inclus dans la livraison standard, consultez donc les instructions d'installation .

Si tout est bien fait, trois fonctions seront à votre disposition. Tout d'abord, nous pouvons obtenir des statistiques:

 postgres=# select * from gist_stat('airports_coordinates_idx'); 

  gist_stat ------------------------------------------ Number of levels: 4 + Number of pages: 690 + Number of leaf pages: 625 + Number of tuples: 7873 + Number of invalid tuples: 0 + Number of leaf tuples: 7184 + Total size of tuples: 354692 bytes + Total size of leaf tuples: 323596 bytes + Total size of index: 5652480 bytes+ (1 row) 

Il est clair que la taille de l'index sur les coordonnées de l'aéroport est de 690 pages et que l'index se compose de quatre niveaux: la racine et deux niveaux internes ont été montrés dans les figures ci-dessus, et le quatrième niveau est feuille.

En fait, l'indice pour huit mille points sera beaucoup plus petit: ici, il a été créé avec un facteur de remplissage de 10% pour plus de clarté.

Deuxièmement, nous pouvons produire l'arbre d'index:

 postgres=# select * from gist_tree('airports_coordinates_idx'); 

  gist_tree ----------------------------------------------------------------------------------------- 0(l:0) blk: 0 numTuple: 5 free: 7928b(2.84%) rightlink:4294967295 (InvalidBlockNumber) + 1(l:1) blk: 335 numTuple: 15 free: 7488b(8.24%) rightlink:220 (OK) + 1(l:2) blk: 128 numTuple: 9 free: 7752b(5.00%) rightlink:49 (OK) + 1(l:3) blk: 57 numTuple: 12 free: 7620b(6.62%) rightlink:35 (OK) + 2(l:3) blk: 62 numTuple: 9 free: 7752b(5.00%) rightlink:57 (OK) + 3(l:3) blk: 72 numTuple: 7 free: 7840b(3.92%) rightlink:23 (OK) + 4(l:3) blk: 115 numTuple: 17 free: 7400b(9.31%) rightlink:33 (OK) + ... 

Et troisièmement, nous pouvons produire les données stockées dans des lignes d'index. Notez la nuance suivante: le résultat de la fonction doit être converti en type de données requis. Dans notre situation, ce type est "boîte" (un rectangle englobant). Par exemple, notez cinq lignes au niveau supérieur:

 postgres=# select level, a from gist_print('airports_coordinates_idx') as t(level int, valid bool, a box) where level = 1; 

  level | a -------+----------------------------------------------------------------------- 1 | (47.663586,80.803207),(-39.2938003540039,-90) 1 | (179.951004028,15.6700000762939),(15.2428998947144,-77.9634017944336) 1 | (177.740997314453,73.5178070068359),(15.0664,10.57970047) 1 | (-77.3191986083984,79.9946975708),(-179.876998901,-43.810001373291) 1 | (-39.864200592041,82.5177993774),(-81.254096984863,-64.2382965088) (5 rows) 

En fait, les chiffres fournis ci-dessus ont été créés uniquement à partir de ces données.

Opérateurs de recherche et de commande

Les opérateurs discutés jusqu'à présent (tels que <@ dans le prédicat p <@ box '(2,1),(7,4)' ) peuvent être appelés opérateurs de recherche car ils spécifient les conditions de recherche dans une requête.

Il existe également un autre type d'opérateur: les opérateurs de commande. Ils sont utilisés pour les spécifications de l'ordre de tri dans la clause ORDER BY au lieu des spécifications conventionnelles des noms de colonne. Voici un exemple d'une telle requête:

 postgres=# select * from points order by p <-> point '(4,7)' limit 2; 

  p ------- (5,5) (7,8) (2 rows) 

p <-> point '(4,7)' est ici une expression qui utilise un opérateur de classement <-> , qui dénote la distance d'un argument à l'autre. La signification de la requête est de renvoyer deux points les plus proches du point (4.7). Une recherche comme celle-ci est connue sous le nom de k-NN - recherche du plus proche voisin.

Pour prendre en charge les requêtes de ce type, une méthode d'accès doit définir une fonction de distance supplémentaire et l'opérateur de commande doit être inclus dans la classe d'opérateur appropriée (par exemple, la classe "points_ops" pour les points). La requête ci-dessous montre les opérateurs, ainsi que leurs types ("s" - recherche et "o" - classement):

 postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'point_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'gist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amoppurpose | amopstrategy -------------------+-------------+-------------- <<(point,point) | s | 1 strictly left >>(point,point) | s | 5 strictly right ~=(point,point) | s | 6 coincides <^(point,point) | s | 10 strictly below >^(point,point) | s | 11 strictly above <->(point,point) | o | 15 distance <@(point,box) | s | 28 contained in rectangle <@(point,polygon) | s | 48 contained in polygon <@(point,circle) | s | 68 contained in circle (9 rows) 

Le nombre de stratégies est également montré, avec leur signification expliquée. Il est clair qu'il existe bien plus de stratégies que pour "btree", seules certaines d'entre elles étant supportées pour les points. Différentes stratégies peuvent être définies pour d'autres types de données.

La fonction distance est appelée pour un élément d'index, et elle doit calculer la distance (en tenant compte de la sémantique de l'opérateur) à partir de la valeur définie par l'expression (" expression d'opérateur de commande de champ indexé ") à l'élément donné. Pour un élément feuille, il s'agit simplement de la distance à la valeur indexée. Pour un élément interne, la fonction doit renvoyer le minimum des distances aux éléments feuille enfant. Étant donné que parcourir toutes les lignes enfants serait assez coûteux, la fonction est autorisée à sous-estimer la distance de manière optimiste, mais au détriment de l'efficacité de la recherche. Cependant, la fonction n'est jamais autorisée à surestimer la distance car cela perturbera le travail de l'index.

La fonction distance peut renvoyer des valeurs de n'importe quel type triable (pour ordonner les valeurs, PostgreSQL utilisera la sémantique de comparaison de la famille d'opérateurs appropriée de la méthode d'accès "btree", comme décrit précédemment ).

Pour les points dans un plan, la distance est interprétée dans un sens très courant: la valeur de (x1,y1) <-> (x2,y2) est égale à la racine carrée de la somme des carrés des différences des abscisses et des ordonnées. La distance entre un point et un rectangle englobant est considérée comme la distance minimale entre le point et ce rectangle ou zéro si le point se trouve à l'intérieur du rectangle. Il est facile de calculer cette valeur sans parcourir les points enfants, et la valeur n'est certainement pas supérieure à la distance à un point enfant.

Considérons l'algorithme de recherche pour la requête ci-dessus.



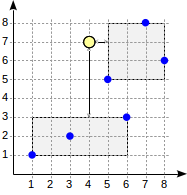
La recherche commence par le nœud racine. Le nœud contient deux rectangles de délimitation. La distance à (1,1) - (6,3) est de 4,0 et à (5,5) - (8,8) est de 1,0.

Les nœuds enfants sont parcourus dans l'ordre d'augmentation de la distance. De cette façon, nous descendons d'abord au nœud enfant le plus proche et calculons les distances aux points (nous afficherons les nombres sur la figure pour la visibilité):



Cette information suffit pour renvoyer les deux premiers points, (5,5) et (7,8). Puisque nous sommes conscients que la distance aux points qui se trouvent dans le rectangle (1,1) - (6,3) est de 4,0 ou plus, nous n'avons pas besoin de descendre jusqu'au premier nœud enfant.

Et si nous devions trouver les trois premiers points?

 postgres=# select * from points order by p <-> point '(4,7)' limit 3; 

  p ------- (5,5) (7,8) (8,6) (3 rows) 

Bien que le deuxième nœud enfant contienne tous ces points, nous ne pouvons pas retourner (8,6) sans regarder dans le premier nœud enfant car ce nœud peut contenir des points plus proches (depuis 4.0 <4.1).



Pour les lignes internes, cet exemple clarifie les exigences de la fonction de distance. En sélectionnant une distance plus petite (4,0 au lieu de 4,5) pour la deuxième ligne, nous avons réduit l'efficacité (l'algorithme a inutilement commencé à examiner un nœud supplémentaire), mais n'a pas brisé l'exactitude de l'algorithme.

Jusqu'à récemment, GiST était la seule méthode d'accès capable de traiter les opérateurs de commande. Mais la situation a changé: la méthode d'accès RUM (à discuter plus loin) a déjà rejoint ce groupe de méthodes, et il n'est pas improbable qu'un bon vieil arbre B les rejoigne: un patch développé par Nikita Glukhov, notre collègue, est en cours discuté par la communauté.

Depuis mars 2019, le support k-NN est ajouté pour SP-GiST dans le prochain PostgreSQL 12 (également écrit par Nikita). Le patch pour B-tree est toujours en cours.

Arborescence R pour les intervalles

Un autre exemple d'utilisation de la méthode d'accès GiST est l'indexation des intervalles, par exemple les intervalles de temps (type "tsrange"). Toute la différence est que les nœuds internes contiendront des intervalles de délimitation au lieu de rectangles de délimitation.

Prenons un exemple simple. Nous allons louer un chalet et enregistrer les intervalles de réservation dans un tableau:

 postgres=# create table reservations(during tsrange); postgres=# insert into reservations(during) values ('[2016-12-30, 2017-01-09)'), ('[2017-02-23, 2017-02-27)'), ('[2017-04-29, 2017-05-02)'); postgres=# create index on reservations using gist(during); 

L'index peut être utilisé pour accélérer la requête suivante, par exemple:

 postgres=# select * from reservations where during && '[2017-01-01, 2017-04-01)'; 

  during ----------------------------------------------- ["2016-12-30 00:00:00","2017-01-08 00:00:00") ["2017-02-23 00:00:00","2017-02-26 00:00:00") (2 rows) 

 postgres=# explain (costs off) select * from reservations where during && '[2017-01-01, 2017-04-01)'; 

  QUERY PLAN ------------------------------------------------------------------------------------ Index Only Scan using reservations_during_idx on reservations Index Cond: (during && '["2017-01-01 00:00:00","2017-04-01 00:00:00")'::tsrange) (2 rows) 

&& opérateur && pour les intervalles indique l'intersection; par conséquent, la requête doit renvoyer tous les intervalles intersectant celui spécifié. Pour un tel opérateur, la fonction de cohérence détermine si l'intervalle donné intersecte avec une valeur dans une ligne interne ou feuille.

Notez qu'il ne s'agit pas d'obtenir des intervalles dans un certain ordre, bien que les opérateurs de comparaison soient définis pour les intervalles. Nous pouvons utiliser l'index "btree" pour les intervalles, mais dans ce cas, nous devrons nous passer de la prise en charge d'opérations comme celles-ci:

 postgres=# select amop.amopopr::regoperator, amop.amoppurpose, amop.amopstrategy from pg_opclass opc, pg_opfamily opf, pg_am am, pg_amop amop where opc.opcname = 'range_ops' and opf.oid = opc.opcfamily and am.oid = opf.opfmethod and amop.amopfamily = opc.opcfamily and am.amname = 'gist' and amop.amoplefttype = opc.opcintype; 

  amopopr | amoppurpose | amopstrategy -------------------------+-------------+-------------- @>(anyrange,anyelement) | s | 16 contains element <<(anyrange,anyrange) | s | 1 strictly left &<(anyrange,anyrange) | s | 2 not beyond right boundary &&(anyrange,anyrange) | s | 3 intersects &>(anyrange,anyrange) | s | 4 not beyond left boundary >>(anyrange,anyrange) | s | 5 strictly right -|-(anyrange,anyrange) | s | 6 adjacent @>(anyrange,anyrange) | s | 7 contains interval <@(anyrange,anyrange) | s | 8 contained in interval =(anyrange,anyrange) | s | 18 equals (10 rows) 

(Sauf l'égalité, qui est contenue dans la classe d'opérateur pour la méthode d'accès "btree".)

Internes

On peut regarder à l'intérieur en utilisant la même extension "gevel". Nous devons seulement nous rappeler de changer le type de données dans l'appel à gist_print:

 postgres=# select level, a from gist_print('reservations_during_idx') as t(level int, valid bool, a tsrange); 

  level | a -------+----------------------------------------------- 1 | ["2016-12-30 00:00:00","2017-01-09 00:00:00") 1 | ["2017-02-23 00:00:00","2017-02-27 00:00:00") 1 | ["2017-04-29 00:00:00","2017-05-02 00:00:00") (3 rows) 

Contrainte d'exclusion

L'index GiST peut être utilisé pour prendre en charge les contraintes d'exclusion (EXCLUDE).

La contrainte d'exclusion garantit que les champs donnés de deux lignes de table ne se "correspondent" pas en fonction de certains opérateurs. Si l'opérateur "égal" est choisi, nous obtenons exactement la contrainte unique: les champs donnés de deux lignes quelconques ne sont pas égaux.

La contrainte d'exclusion est prise en charge par l'index, ainsi que la contrainte unique. Nous pouvons choisir n'importe quel opérateur pour que:

1. Il est pris en charge par la méthode d'index - propriété "can_exclude" (par exemple, "btree", GiST ou SP-GiST, mais pas GIN).
2. Elle est commutative, c'est-à-dire que la condition est remplie: a opérateur b = b opérateur a.

Voici une liste de stratégies appropriées et d'exemples d'opérateurs (les opérateurs, comme nous nous en souvenons, peuvent avoir des noms différents et ne pas être disponibles pour tous les types de données):

• Pour "btree":
  
  • "Égale" =
• Pour GiST et SP-GiST:
  
  • "Intersection" &&
  • "Coïncidence" ~=
  • Adjacence -|-

Notez que nous pouvons utiliser l'opérateur d'égalité dans une contrainte d'exclusion, mais ce n'est pas pratique: une contrainte unique sera plus efficace. C'est exactement pourquoi nous n'avons pas abordé les contraintes d'exclusion lorsque nous avons discuté des arbres B.

Donnons un exemple d'utilisation d'une contrainte d'exclusion. Il est raisonnable de ne pas autoriser de réservations pour des intervalles qui se croisent.

 postgres=# alter table reservations add exclude using gist(during with &&); 

Une fois que nous avons créé la contrainte d'exclusion, nous pouvons ajouter des lignes:

 postgres=# insert into reservations(during) values ('[2017-06-10, 2017-06-13)'); 

Mais une tentative d'insérer un intervalle d'intersection dans la table entraînera une erreur:

 postgres=# insert into reservations(during) values ('[2017-05-15, 2017-06-15)'); 

 ERROR: conflicting key value violates exclusion constraint "reservations_during_excl" DETAIL: Key (during)=(["2017-05-15 00:00:00","2017-06-15 00:00:00")) conflicts with existing key (during)=(["2017-06-10 00:00:00","2017-06-13 00:00:00")). 

Extension "Btree_gist"

Compliquons le problème. Nous développons notre modeste activité, et nous allons louer plusieurs chalets:

 postgres=# alter table reservations add house_no integer default 1; 

Nous devons changer la contrainte d'exclusion afin que les numéros de maison soient pris en compte. GiST, cependant, ne prend pas en charge l'opération d'égalité pour les nombres entiers:

 postgres=# alter table reservations drop constraint reservations_during_excl; postgres=# alter table reservations add exclude using gist(during with &&, house_no with =); 

 ERROR: data type integer has no default operator class for access method "gist" HINT: You must specify an operator class for the index or define a default operator class for the data type. 

Dans ce cas, l'extension " btree_gist " sera utile, ce qui ajoute la prise en charge GiST des opérations inhérentes aux arbres B. GiST, à terme, peut prendre en charge tous les opérateurs, alors pourquoi ne devrions-nous pas lui apprendre à prendre en charge les opérateurs «plus grands», «moins» et «égaux»?

 postgres=# create extension btree_gist; postgres=# alter table reservations add exclude using gist(during with &&, house_no with =); 

Maintenant, nous ne pouvons toujours pas réserver le premier chalet pour les mêmes dates:

 postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 1); 

 ERROR: conflicting key value violates exclusion constraint "reservations_during_house_no_excl" 

Cependant, nous pouvons réserver le second:

 postgres=# insert into reservations(during, house_no) values ('[2017-05-15, 2017-06-15)', 2); 

Mais sachez que bien que GiST puisse en quelque sorte prendre en charge les opérateurs "supérieurs", "inférieurs" et "égaux", B-tree le fait toujours mieux. Il ne vaut donc la peine d'utiliser cette technique que si l'index GiST est essentiellement nécessaire, comme dans notre exemple.

Arbre RD pour la recherche en texte intégral

À propos de la recherche en texte intégral

Commençons par une introduction minimaliste à la recherche en texte intégral de PostgreSQL (si vous êtes au courant, vous pouvez ignorer cette section).

La tâche de recherche en texte intégral consiste à sélectionner dans l'ensemble de documents les documents qui correspondent à la requête de recherche. (S'il existe de nombreux documents correspondants, il est important de trouver la meilleure correspondance , mais nous n'en dirons rien à ce stade.)

À des fins de recherche, un document est converti en un type spécialisé "tsvector", qui contient des lexèmes et leurs positions dans le document. Les lexèmes sont des mots convertis au format approprié pour la recherche. Par exemple, les mots sont généralement convertis en minuscules et les terminaisons variables sont coupées:

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile'); 

  to_tsvector ----------------------------------------- 'crook':4,10 'man':5 'mile':11 'walk':8 (1 row) 

Nous pouvons également voir que certains mots (appelés mots vides ) sont totalement supprimés ("là", "était", "un", "et", "il") car ils se produisent probablement trop souvent pour que leur recherche ait un sens. Toutes ces conversions peuvent certainement être configurées, mais c'est une autre histoire.

Une requête de recherche est représentée avec un autre type: "tsquery". En gros, une requête consiste en un ou plusieurs lexèmes joints par des connecteurs: "et" &, "ou" |, "pas"! .. Nous pouvons également utiliser des parenthèses pour clarifier la priorité des opérations.

 postgres=# select to_tsquery('man & (walking | running)'); 

  to_tsquery ---------------------------- 'man' & ( 'walk' | 'run' ) (1 row) 

Un seul opérateur de correspondance @@ est utilisé pour la recherche en texte intégral.

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile') @@ to_tsquery('man & (walking | running)'); 

  ?column? ---------- t (1 row) 

 postgres=# select to_tsvector('There was a crooked man, and he walked a crooked mile') @@ to_tsquery('man & (going | running)'); 

  ?column? ---------- f (1 row) 

Cette information suffit pour l'instant. Nous approfondirons un peu la recherche en texte intégral dans un prochain article qui présente l'index GIN.

Arbres RD

Pour une recherche de texte intégral rapide, d'une part, la table doit stocker une colonne de type "tsvector" (pour éviter d'effectuer une conversion coûteuse à chaque fois lors de la recherche) et d'autre part, un index doit être construit sur cette colonne. GiST est l'une des méthodes d'accès possibles pour cela.

 postgres=# create table ts(doc text, doc_tsv tsvector); postgres=# create index on ts using gist(doc_tsv); postgres=# insert into ts(doc) values ('Can a sheet slitter slit sheets?'), ('How many sheets could a sheet slitter slit?'), ('I slit a sheet, a sheet I slit.'), ('Upon a slitted sheet I sit.'), ('Whoever slit the sheets is a good sheet slitter.'), ('I am a sheet slitter.'), ('I slit sheets.'), ('I am the sleekest sheet slitter that ever slit sheets.'), ('She slits the sheet she sits on.'); postgres=# update ts set doc_tsv = to_tsvector(doc); 

Il est, certes, commode de confier un déclencheur à la dernière étape (conversion du document en "tsvector").

 postgres=# select * from ts; 

 -[ RECORD 1 ]---------------------------------------------------- doc | Can a sheet slitter slit sheets? doc_tsv | 'sheet':3,6 'slit':5 'slitter':4 -[ RECORD 2 ]---------------------------------------------------- doc | How many sheets could a sheet slitter slit? doc_tsv | 'could':4 'mani':2 'sheet':3,6 'slit':8 'slitter':7 -[ RECORD 3 ]---------------------------------------------------- doc | I slit a sheet, a sheet I slit. doc_tsv | 'sheet':4,6 'slit':2,8 -[ RECORD 4 ]---------------------------------------------------- doc | Upon a slitted sheet I sit. doc_tsv | 'sheet':4 'sit':6 'slit':3 'upon':1 -[ RECORD 5 ]---------------------------------------------------- doc | Whoever slit the sheets is a good sheet slitter. doc_tsv | 'good':7 'sheet':4,8 'slit':2 'slitter':9 'whoever':1 -[ RECORD 6 ]---------------------------------------------------- doc | I am a sheet slitter. doc_tsv | 'sheet':4 'slitter':5 -[ RECORD 7 ]---------------------------------------------------- doc | I slit sheets. doc_tsv | 'sheet':3 'slit':2 -[ RECORD 8 ]---------------------------------------------------- doc | I am the sleekest sheet slitter that ever slit sheets. doc_tsv | 'ever':8 'sheet':5,10 'sleekest':4 'slit':9 'slitter':6 -[ RECORD 9 ]---------------------------------------------------- doc | She slits the sheet she sits on. doc_tsv | 'sheet':4 'sit':6 'slit':2 

Comment l’indice doit-il être structuré? L'utilisation directe de R-tree n'est pas une option car on ne sait pas comment définir un "rectangle englobant" pour les documents. Mais nous pouvons appliquer une certaine modification de cette approche pour les ensembles, un soi-disant arbre RD (RD signifie "Russian Doll"). Un ensemble est considéré comme un ensemble de lexèmes dans ce cas, mais en général, un ensemble peut être n'importe lequel.

Une idée des arbres RD est de remplacer un rectangle englobant par un ensemble englobant, c'est-à-dire un ensemble contenant tous les éléments des ensembles enfants.

Une question importante se pose de savoir comment représenter les ensembles dans les lignes d'index. La manière la plus simple consiste simplement à énumérer tous les éléments de l'ensemble. Cela pourrait ressembler à ceci:



Ensuite, par exemple, pour l'accès par la condition doc_tsv @@ to_tsquery('sit') nous ne pouvions descendre que vers les nœuds qui contiennent le lexème "sit":



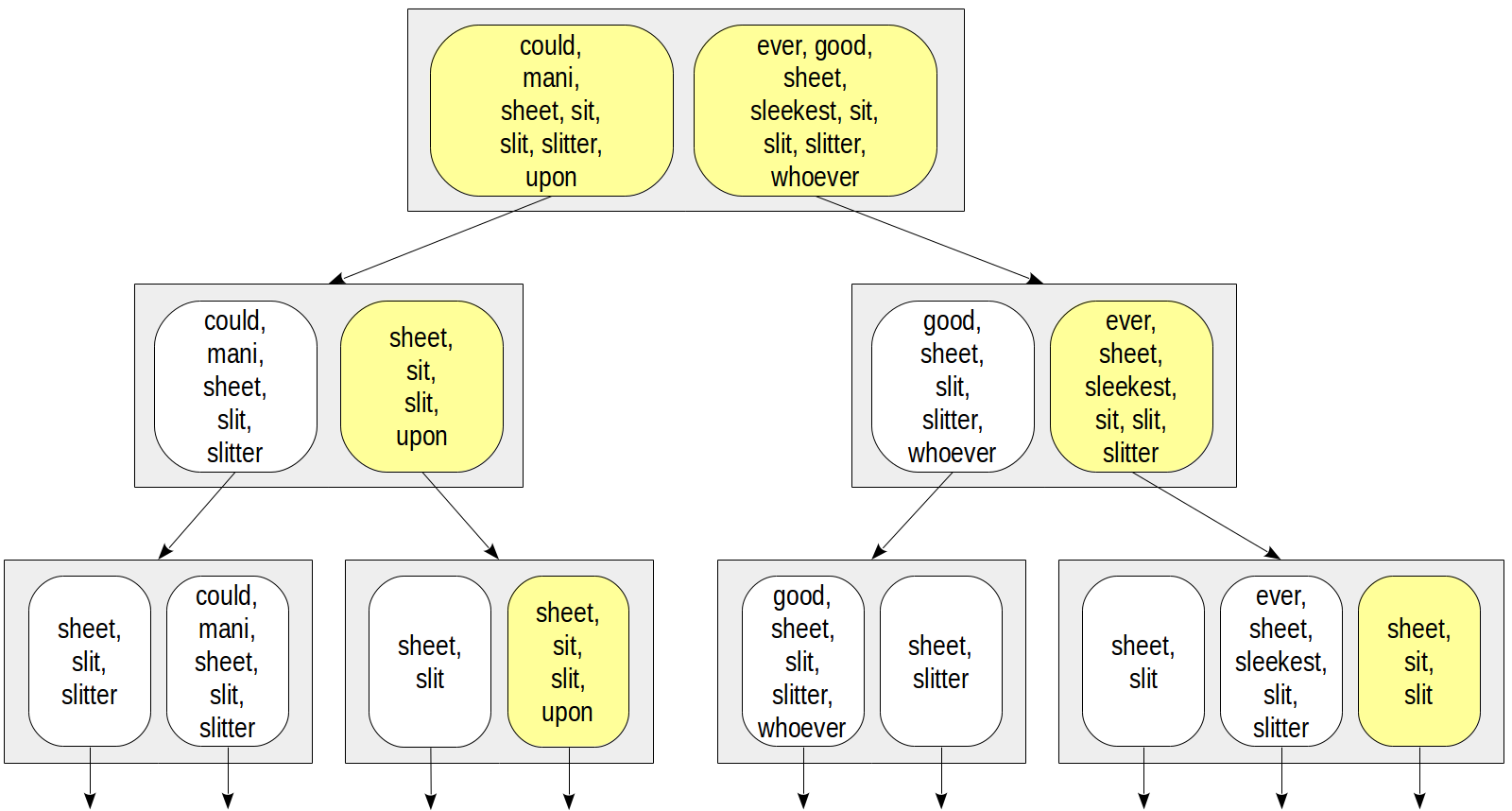
Cette représentation présente des problèmes évidents. Le nombre de lexèmes dans un document peut être assez important, les lignes d'index auront donc une grande taille et entreront dans TOAST, ce qui rend l'index beaucoup moins efficace. Même si chaque document a peu de lexèmes uniques, l'union des ensembles peut toujours être très grande: plus la racine est élevée, plus les lignes d'index sont grandes.

Une représentation comme celle-ci est parfois utilisée, mais pour d'autres types de données. Et la recherche en texte intégral utilise une autre solution, plus compacte - un soi-disant arbre de signature . Son idée est bien connue de tous ceux qui ont traité du filtre Bloom.

Chaque lexème peut être représenté avec sa signature : une chaîne de bits d'une certaine longueur où tous les bits sauf un sont nuls. La position de ce bit est déterminée par la valeur de la fonction de hachage du lexème (nous avons discuté précédemment des fonctions internes des fonctions de hachage).

La signature du document est le OU au niveau du bit des signatures de tous les lexèmes de document.

Supposons les signatures de lexèmes suivantes:

 pourrait 1000000
 jamais 0001000
 bon 0000010
 mani 0000100
 feuille 0000100
 0100000 le plus élégant
 asseoir 0010000
 fente 0001000
 refendeur 0000001
 au 0000010
 quiconque 0010000

Ensuite, les signatures des documents sont comme celles-ci:

 Une feuille peut-elle refendre des feuilles fendues?  0001101
 Combien de feuilles une fente-feuille peut-elle refendre?  1001101
 J'ai fendu une feuille, une feuille que j'ai fendue.  0001100
 Sur une feuille fendue, je m'assois.  0011110
 Celui qui a fendu les feuilles est un bon refendeur de feuilles.  0011111
 Je suis une découpeuse de feuilles.  0000101
 J'ai fendu des draps.  0001100
 Je suis la découpeuse de feuilles la plus élégante qui ait jamais fendu des feuilles.  0101101
 Elle fend le drap sur lequel elle est assise.  0011100

L'arbre d'index peut être représenté comme suit:



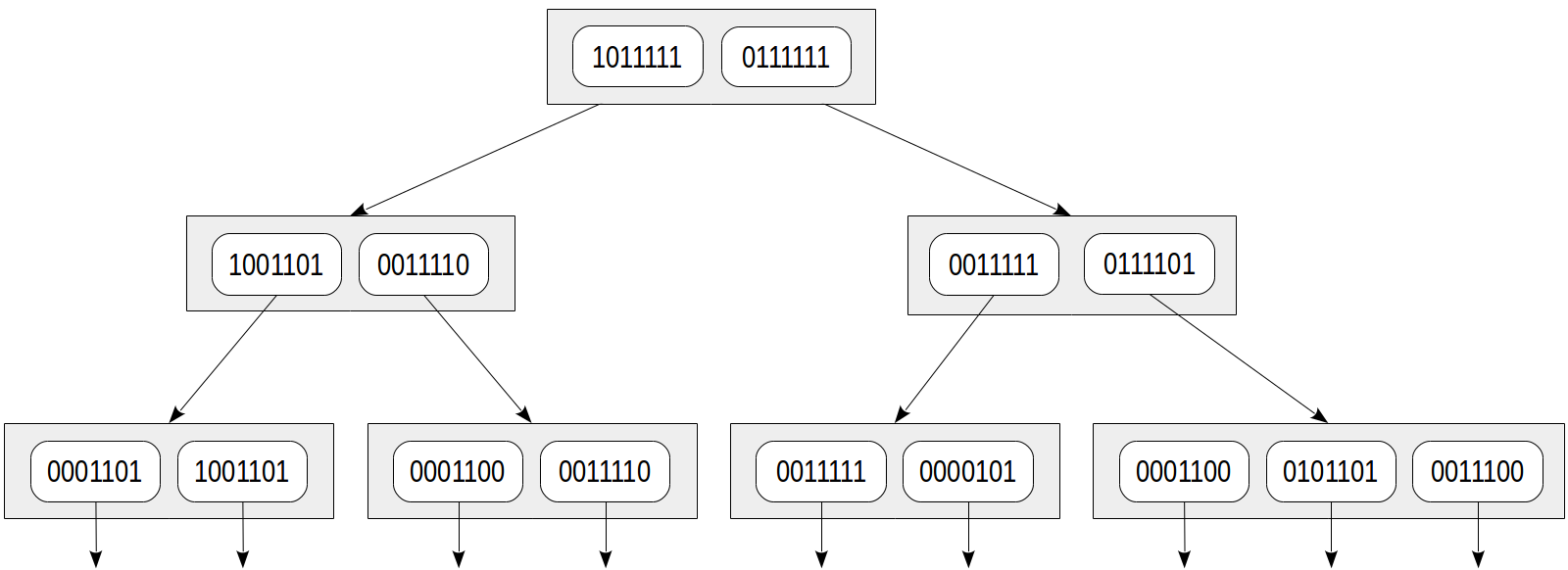
Les avantages de cette approche sont évidents: les lignes d'index ont des tailles égales et un tel index est compact. Mais un inconvénient est également clair: la précision est sacrifiée à la compacité.

Considérons la même condition doc_tsv @@ to_tsquery('sit') . Et calculons la signature de la requête de recherche de la même manière que pour le document: 0010000 dans ce cas. La fonction de cohérence doit renvoyer tous les nœuds enfants dont les signatures contiennent au moins un bit de la signature de requête:



Comparez avec la figure ci-dessus: nous pouvons voir que l'arbre est devenu jaune, ce qui signifie que des faux positifs se produisent et que des nœuds excessifs sont passés pendant la recherche. Ici, nous avons ramassé le lexème "qui que ce soit", dont la signature était malheureusement la même que la signature du lexème "assis". Il est important qu'aucun faux négatif ne puisse se produire dans le motif, c'est-à-dire que nous sommes sûrs de ne pas manquer les valeurs nécessaires.

En outre, il peut arriver que différents documents obtiennent également les mêmes signatures: dans notre exemple, les documents malchanceux sont "je tranche une feuille, une feuille je tranche" et "je tranche des feuilles" (les deux portent la signature 0001100). Et si une ligne d'index feuille ne stocke pas la valeur de "tsvector", l'index lui-même donnera des faux positifs. Bien sûr, dans ce cas, la méthode demandera au moteur d'indexation de revérifier le résultat avec la table, de sorte que l'utilisateur ne verra pas ces faux positifs. Mais l'efficacité de la recherche peut être compromise.

En fait, une signature fait 124 octets dans l'implémentation actuelle au lieu de 7 bits dans les figures, donc les problèmes ci-dessus sont beaucoup moins susceptibles de se produire que dans l'exemple. Mais en réalité, beaucoup plus de documents sont également indexés. Pour réduire en quelque sorte le nombre de faux positifs de la méthode d'indexation, l'implémentation devient un peu délicate: le "tsvector" indexé est stocké dans une ligne d'index feuille, mais seulement si sa taille n'est pas grande (un peu moins de 1/16 de une page, soit environ un demi-kilo-octet pour les pages de 8 Ko).

Exemple

Pour voir comment l'indexation fonctionne sur des données réelles, prenons l'archive des e-mails "pgsql-hackers". La version utilisée dans l'exemple contient 356125 messages avec la date d'envoi, le sujet, l'auteur et le texte:

 fts=# select * from mail_messages order by sent limit 1; 

 -[ RECORD 1 ]------------------------------------------------------------------------ id | 1572389 parent_id | 1562808 sent | 1997-06-24 11:31:09 subject | Re: [HACKERS] Array bug is still there.... author | "Thomas G. Lockhart" <Thomas.Lockhart@jpl.nasa.gov> body_plain | Andrew Martin wrote: + | > Just run the regression tests on 6.1 and as I suspected the array bug + | > is still there. The regression test passes because the expected output+ | > has been fixed to the *wrong* output. + | + | OK, I think I understand the current array behavior, which is apparently+ | different than the behavior for v1.0x. + ... 

Ajout et remplissage de la colonne de type "tsvector" et construction de l'index. Ici, nous joindrons trois valeurs dans un vecteur (sujet, auteur et texte du message) pour montrer que le document n'a pas besoin d'être un champ, mais peut être composé de parties arbitraires totalement différentes.

 fts=# alter table mail_messages add column tsv tsvector; fts=# update mail_messages set tsv = to_tsvector(subject||' '||author||' '||body_plain); 

 NOTICE: word is too long to be indexed DETAIL: Words longer than 2047 characters are ignored. ... UPDATE 356125 

 fts=# create index on mail_messages using gist(tsv); 

Comme nous pouvons le voir, un certain nombre de mots ont été supprimés en raison d'une taille trop grande. Mais l'index est finalement créé et peut prendre en charge les requêtes de recherche:

 fts=# explain (analyze, costs off) select * from mail_messages where tsv @@ to_tsquery('magic & value'); 

  QUERY PLAN ---------------------------------------------------------- Index Scan using mail_messages_tsv_idx on mail_messages (actual time=0.998..416.335 rows=898 loops=1) Index Cond: (tsv @@ to_tsquery('magic & value'::text)) Rows Removed by Index Recheck: 7859 Planning time: 0.203 ms Execution time: 416.492 ms (5 rows) 

Nous pouvons voir qu'avec 898 lignes correspondant à la condition, la méthode d'accès a renvoyé 7859 lignes supplémentaires qui ont été filtrées en revérifiant avec la table. Cela démontre un impact négatif de la perte de précision sur l'efficacité.

Internes

Pour analyser le contenu de l'index, nous utiliserons à nouveau l'extension "gevel":

 fts=# select level, a from gist_print('mail_messages_tsv_idx') as t(level int, valid bool, a gtsvector) where a is not null; 

  level | a -------+------------------------------- 1 | 992 true bits, 0 false bits 2 | 988 true bits, 4 false bits 3 | 573 true bits, 419 false bits 4 | 65 unique words 4 | 107 unique words 4 | 64 unique words 4 | 42 unique words ... 

Les valeurs du type spécialisé "gtsvector" qui sont stockées dans des lignes d'index sont en fait la signature plus, peut-être, la source "tsvector". Si le vecteur est disponible, la sortie contient le nombre de lexèmes (mots uniques), sinon, le nombre de vrais et faux bits dans la signature.

Il est clair que dans le nœud racine, la signature a dégénéré en "tous les uns", c'est-à-dire qu'un niveau d'index est devenu absolument inutile (et un autre est devenu presque inutile, avec seulement quatre faux bits).

Propriétés

Examinons les propriétés de la méthode d'accès GiST (des requêtes ont été fournies plus tôt ):

  amname | name | pg_indexam_has_property --------+---------------+------------------------- gist | can_order | f gist | can_unique | f gist | can_multi_col | t gist | can_exclude | t 

Le tri des valeurs et la contrainte unique ne sont pas pris en charge. Comme nous l'avons vu, l'index peut être construit sur plusieurs colonnes et utilisé dans les contraintes d'exclusion.

Les propriétés de couche d'index suivantes sont disponibles:

  name | pg_index_has_property ---------------+----------------------- clusterable | t index_scan | t bitmap_scan | t backward_scan | f 

Et les propriétés les plus intéressantes sont celles de la couche de colonne. Certaines propriétés sont indépendantes des classes d'opérateurs:

  name | pg_index_column_has_property --------------------+------------------------------ asc | f desc | f nulls_first | f nulls_last | f orderable | f search_array | f search_nulls | t 

(Le tri n'est pas pris en charge; l'index ne peut pas être utilisé pour rechercher un tableau; les valeurs NULL sont prises en charge.)

Mais les deux propriétés restantes, "distance_orderable" et "returnable", dépendront de la classe d'opérateur utilisée. Par exemple, pour les points, nous obtiendrons:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | t returnable | t 

La première propriété indique que l'opérateur de distance est disponible pour rechercher les voisins les plus proches. Et le second indique que l'index peut être utilisé pour l'analyse uniquement par index. Bien que les lignes d'index des feuilles stockent des rectangles plutôt que des points, la méthode d'accès peut renvoyer ce qui est nécessaire.

Voici les propriétés des intervalles:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | f returnable | t 

Pour les intervalles, la fonction de distance n'est pas définie et par conséquent, la recherche des voisins les plus proches n'est pas possible.

Et pour la recherche plein texte, nous obtenons:

  name | pg_index_column_has_property --------------------+------------------------------ distance_orderable | f returnable | f 

La prise en charge de l'analyse d'index uniquement a été perdue car les lignes de feuille peuvent contenir uniquement la signature sans les données elles-mêmes. Cependant, il s'agit d'une perte mineure car personne ne s'intéresse de toute façon à la valeur de type "tsvector": cette valeur est utilisée pour sélectionner des lignes, alors que c'est le texte source qui doit être affiché, mais qui est de toute façon manquant dans l'index.

Autres types de données

Enfin, nous mentionnerons quelques autres types qui sont actuellement pris en charge par la méthode d'accès GiST en plus des types géométriques déjà discutés (par exemple de points), des intervalles et des types de recherche en texte intégral.

Parmi les types standard, il s'agit du type " inet " pour les adresses IP. Tout le reste est ajouté via des extensions:

• cube fournit le type de données "cube" pour les cubes multidimensionnels. Pour ce type, tout comme pour les types géométriques dans un plan, la classe d'opérateur GiST est définie: R-tree, prenant en charge la recherche des plus proches voisins.
  
• seg fournit le type de données "seg" pour les intervalles avec des limites spécifiées avec une certaine précision et ajoute la prise en charge de l'index GiST pour ce type de données (arbre R).
  
• intarray étend les fonctionnalités des tableaux entiers et leur prend en charge GiST. Deux classes d'opérateurs sont implémentées: "gist__int_ops" (arbre RD avec une représentation complète des clés dans les lignes d'index) et "gist__bigint_ops" (arbre RD de signature). La première classe peut être utilisée pour les petits tableaux, et la seconde - pour les plus grandes tailles.
  
• ltree ajoute le type de données «ltree» pour les structures arborescentes et la prise en charge GiST pour ce type de données (RD-tree).
  
• pg_trgm ajoute une classe d'opérateur spécialisée "gist_trgm_ops" pour l'utilisation des trigrammes dans la recherche en texte intégral. Mais cela doit être discuté plus loin, avec l'indice GIN.
  

Continuez à lire .