Je rappelle une conclusion importante des parties précédentes. Pour un comportement séquentiel cyclique qui ne contient pas plusieurs signaux (commutation sur un cycle plus de deux fois), la fonction logique minimale de chaque signal peut être représentée sous la forme suivante (naturellement, en l'absence de conflits CSC):
1)
où a * b * ... * c est l'implicant d'une ou plusieurs variables. g + h + ... + i - il s'agit peut-être d'un ensemble vide d'implicants composé d'une variable. x * f est un implant de 2 variables, dont la présence sous une forme minimale n'est pas nécessaire. Toutes les variables, à l'exception de x, peuvent être incluses dans la formule sous forme directe et inverse, selon la disposition des signes des événements correspondants. Toutes les variables sont incluses dans la formule comme arguments strictement une fois.
Avant de poursuivre, nous allons regarder de plus près un phénomène comme la décomposition. Tout d'abord, la décomposition présente un intérêt, ce qui préserve l'auto-synchronisation. Lors de la décomposition d'une fonction logique NON-ET-OU, on peut distinguer comme un nouvel élément:
a) un ou plusieurs implicants,
b) plusieurs signaux (variables) d'un implant,
c) un onduleur d'entrée.
Pour commencer, nous considérons un cas particulier de la fonction NOR AND. Le comportement d'une telle fonction logique (x = a + b + c + d) pour le modèle en question:
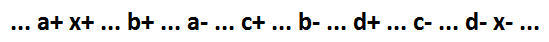
Elle peut distinguer plusieurs signaux comme un élément distinct.
En fait, la sélection d'un nouvel élément lors de la décomposition est l'addition d'un nouveau signal (f). Afin de maintenir un comportement correct, une semi-modularité et une auto-synchronisation, la commutation du signal f nouvellement ajouté doit avoir des événements de conséquence. Puisque la décomposition affecte seulement un élément du circuit (dans ce cas, x) et n'affecte pas les éléments restants du circuit, la commutation du signal f ne peut provoquer que la commutation du signal x. Sinon, la fonction logique d'un autre signal dépendrait du signal f. Étant donné cette conclusion, essayons de mettre en évidence plusieurs variables à l'exception de la variable a en tant que nouvel élément f. Prenons par exemple les variables b et c. Ils forment l'élément logique f = b + c.
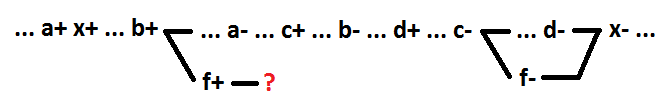
Comme on peut le voir, pour l'événement f +, il est impossible de déterminer l'événement de conséquence sans violer l'exactitude du comportement. Tout groupe de signaux qui ne contient pas la variable a ne peut pas être alloué en tant qu'élément séparé tout en conservant l'auto-synchronisation.
Un signal tel que dans cet exemple sera appelé mise sous tension. Dans le cas général, le signal de commutation pour la fonction OU (ET) est un signal, sa commutation sur 1 (0) modifie la valeur de la fonction de 0 à 1 (de 1 à 0). Pour maintenir l'auto-synchronisation pendant la décomposition de la fonction logique OU (ET) lors de la sélection d'un nouvel élément, vous devez utiliser le signal de commutation. Lors de la sélection d'un nouvel élément, il est également nécessaire d'utiliser uniquement les signaux formant une chaîne connectée (dans l'exemple ci-dessous a + b). x = f + c + d, f = a + b.
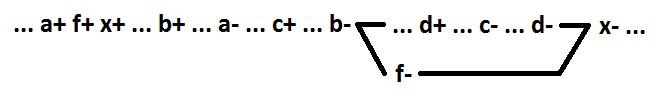
Lors de l'utilisation de signaux a + b + d, l'auto-synchronisation n'est pas préservée.
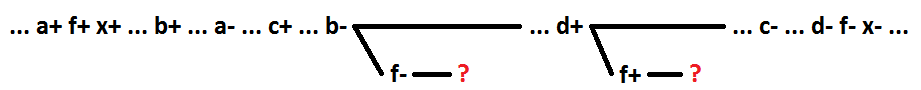
Ainsi, pour des comportements séquentiels sans signaux multiples lors de la décomposition de la fonction logique OR (I), mettre en évidence comme nouvel élément les premiers au cours du déploiement du processus de signal, à partir de la commutation, garantit l'auto-synchronisation du circuit.
Considérons maintenant la fonction non-OU (x =! A +! B). En tant qu'élément séparé (f) tout en conservant l'auto-synchronisation, seul l'inverseur d'entrée correspondant au signal de commutation (x = f +! B, f =! A) peut être sélectionné. La séparation des autres onduleurs d'entrée en tant qu'élément séparé entraînera une violation de l'auto-synchronisation.
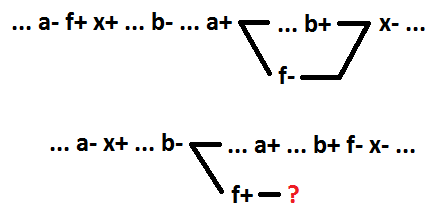
Passons à la fonction AND-OR. De même, en tant que signal de commutation pour la fonction OU, nous définissons l'implicant de commutation pour la fonction ET-OU. Il s'agit d'un implicant dont la modification de la valeur de 0 à 1 entraîne une modification de la valeur de la fonction de 0 à 1. De même, comme cela a été découvert pour la fonction OU, pour les comportements séquentiels sans signaux multiples lors de la décomposition de la fonction logique ET-OU, en sélectionnant les premiers comme nouvel élément en cours de déploiement, l'implicant, à commencer par l'inclusion, garantit la préservation de l'auto-synchronisation du circuit. Sinon, l'auto-synchronisation sera interrompue. Dans l'exemple ci-dessous, avant décomposition x = a * b + c. Après décomposition, x = f + c, f = a * b.
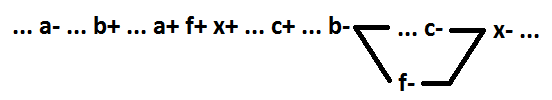
Maintenant pour la fonction ET-OU, nous considérons la sélection comme un nouvel élément de plusieurs variables incluses dans le même implicant. Seules les fonctions minimales sont prises en compte. Voici toutes les options possibles pour l'exemple de la fonction x = a * b * c + d (pour l'option 4 - x = a * b * c + d + e, pour l'option 6 - x = a * b * c * d + e) . L'élément en surbrillance est f = a * b.

Dans l'option 1, la commutation de l'un des signaux attribués (a +) est la cause de l'événement x +. Dans l'option 2, la commutation de l'un des signaux attribués (a-) est la cause de l'événement x. Dans les options 3 et 4, la commutation de l'un des signaux attribués (respectivement a + et a-) se situe entre les événements x + et x-, et n'est pas la cause de l'événement x-. L'option 5 est un cas particulier de l'option 4, lorsque l'implicant, dans lequel les signaux sont attribués, est inclusif. L'option restante 6 - toutes les commutations des signaux attribués sont situées entre les événements x- et x +, et ne sont pas les causes de l'événement x +.
Comme vous pouvez le voir, dans les options 1 et 6, l'événement f- ne peut pas être positionné correctement. De telles transformations ne sont pas une décomposition avec préservation de l'auto-synchronisation. Dans les options 2, 3 et 4, l'auto-synchronisation est conservée. Mais la valeur de la fonction x s'avère différente de f * c + d (f * c + d + e pour 4 options). Pour 2 options - x = f * (d + c), pour 3 options x = c * x + d *! F + x *! F, pour 4 options x = (f + d) * (e + c). De telles transformations ne sont pas des décompositions.
Seule l'option 5 est une décomposition avec préservation de l'auto-synchronisation (x = f * c + d). Dans ce cas, en tant qu'élément séparé dans l'implicant d'inclusion, les premiers signaux sont sélectionnés, en commençant par l'inclusion (le signal incluant l'implicant de And est le même que le signal incluant la fonction de AND). Mais, comme indiqué ci-dessus, un résultat similaire est obtenu en deux étapes. Tout d'abord, l'inclusion de l'implant est mise en évidence. À la deuxième étape, les premiers signaux sont sélectionnés dans le nouvel élément, en commençant par le signal de commutation.
Passons à la fonction NON-ET-OU. Considérons l'onduleur d'entrée comme un élément distinct. Le signal a correspond à l'entrée de l'élément x, à laquelle un inverseur d'entrée dédié est connecté (f =! A).
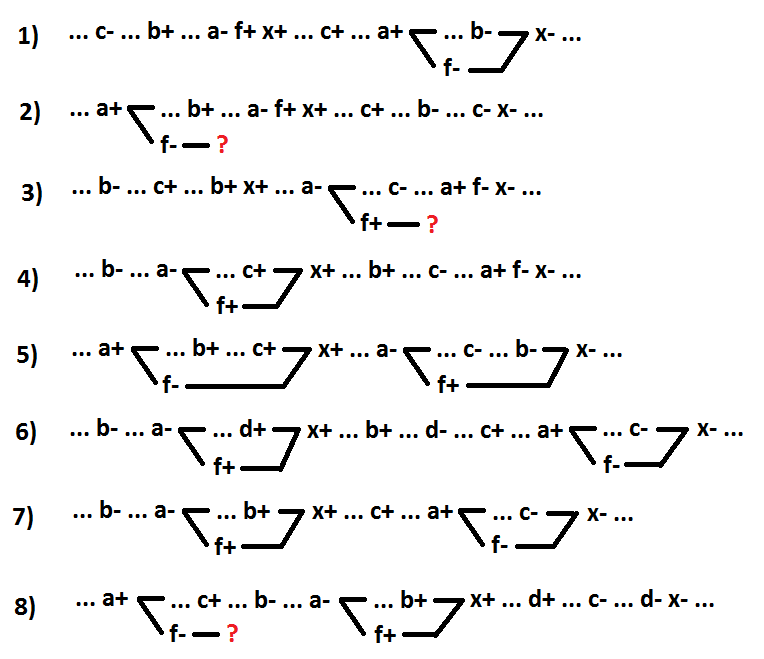
Options 1 et 2 - le signal de commutation a est la cause de l'événement x + (1 - x =! A + b * c, 2 - x = b *! A + c). Options 3 et 4 - la commutation du signal a est la cause de l'événement x- (3 - x =! A + b * c, 4 - x =! A * b + c). Options 5 et 6 - la commutation du signal a se situe entre les événements x + et x-, et n'est pas la cause de l'événement x- (5 - x = b *! A + c, 6 - x =! A * b + d + c). L'option 7 est un cas particulier de l'option 6, lorsque le signal a est un signal de commutation comprenant des implicants (x =! A * b + c). L'option restante 8 - tous les commutateurs de signaux a sont situés entre les événements x- et x +, et ne sont pas les causes de l'événement x + (x = c *! A * b + d).
Comme vous pouvez le voir, les options 2, 3 et 8 ne sont pas une décomposition avec conservation de l'auto-synchronisation, car il est impossible de positionner correctement la commutation de signal f. Pour l'option 4, après la conversion x = f * (c + b). Pour l'option 5, après la conversion x = c *! F +! F * x + b * x. Pour l'option 6, après la conversion x = (f + c) * (d + b). Ces transformations (options 4, 5 et 6) ne sont pas des décompositions. Pour l'option 7, après la conversion x = f * b + c. L'option 7 est une décomposition avec préservation de l'auto-synchronisation. Dans ce cas, un onduleur correspondant au signal de commutation incluant les implants est attribué en tant qu'élément séparé. Un résultat similaire est obtenu en deux étapes en utilisant les transformations ci-dessus. Tout d'abord, l'inclusion de l'implicant est mise en évidence, puis l'inverseur d'entrée du signal d'activation lui est alloué. Pour l'option 1, après la conversion x = f + b * c. L'option 1 est également une décomposition avec préservation de l'auto-synchronisation. Il s'agit d'un cas particulier de l'option 7, lorsque l'inclusion de l'implicant consiste en un signal.
Nous systématisons les résultats obtenus. Pour le modèle considéré, lors de la décomposition d'une fonction logique NON-ET-OU pour maintenir l'auto-synchronisme, seules les transformations suivantes sont possibles - allocation en tant qu'élément distinct:
1 - un ou plusieurs, à partir de l'implicatif inclusif se chevauchant (cas particulier - pour la fonction de sélection NON-OU de plusieurs signaux se chevauchant, à partir de l'inclusif);
2 - dans l'inclusion impliquée de plusieurs, à partir de l'inclusion, des signaux se chevauchant;
3 - onduleur d'entrée correspondant au signal de commutation, y compris les implicants (cas particulier - pour la fonction de sélection NON-OU de l'onduleur d'entrée correspondant au signal de commutation).
Ces transformations ne permettent pas à l'implicant d'être inclusif s'il n'était pas avant la transformation. D'où la conclusion: si une fonction logique contient un implicant, qui se compose de plusieurs signaux et n'est pas inclusif, une telle fonction ne peut pas être fragmentée à l'aide d'une décomposition qui préserve l'auto-synchronisation, jusqu'à deux éléments d'entrée. Toute fonction logique NON-ET-OU dans laquelle plus d'une variable ne contient qu'un implicant inclusif peut être divisée en éléments à deux entrées (2I-NOT, 2OR-NOT) à l'aide d'une décomposition qui préserve l'auto-synchronisation.
Étape 1 - si l'élément logique ne contient qu'un seul implicant (ou si tous les implicants sont constitués d'une seule variable), passez à l'étape 3, sinon passez à l'étape 2.
Étape 2 - sélectionnez comme élément séparé tous les implants, sauf un, en commençant par l'inclusion. Ensuite, nous travaillons avec l'élément nouvellement reçu. Passez à l'étape 1.
Étape 3 - si l'élément se compose de deux variables, passez à l'étape 5, sinon passez à l'étape 4.
Étape 4 - nous sélectionnons comme élément séparé toutes les variables, sauf une, en commençant par l'inclusion. Ensuite, nous travaillons avec l'élément nouvellement reçu. Passez à l'étape 3.
Étape 5 - s'applique à tous les éléments à deux entrées reçus.
Étape 5.1 - si les onduleurs d'entrée sont sur les deux entrées, nous convertirons l'élément en double.
Étape 5.2 - si l'onduleur d'entrée est un et correspond à un signal qui ne s'allume pas, nous convertirons l'élément en double.
Étape 5.3 - l'onduleur d'entrée, le cas échéant, est mis en évidence en tant qu'élément distinct. Concassage terminé.
Revenons maintenant à la formule 1 au début du texte. Si l'implicant x * f n'est pas dans l'expression logique, alors la fonction ressemble à ceci: x = a * b * c + g + h + i. Son comportement:
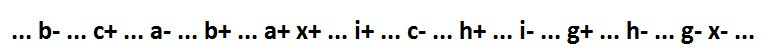
Comme vous pouvez le voir, le seul implicant de plus d'une variable (a * b * c) est inclusif. Et cette fonction à l'aide de la décomposition peut être fragmentée en composants minimum tout en maintenant l'auto-synchronisation.
Si l'impliquant x * f est présent dans une expression logique, alors la fonction ressemble à ceci: x = a * b * c + x * f + g + h + i. Son comportement:
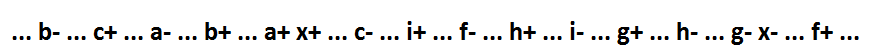
L'implicant x * f non inclus se compose de plusieurs variables. Une telle fonction ne peut pas être fragmentée tout en conservant l'auto-synchronisation. Mais nous appliquons une transformation qui préserve l'auto-synchronisation: ajoutez le signal y - dual au signal x. L'ajout du signal y modifie uniquement la fonction du signal x et du signal, dont la commutation était une conséquence de l'événement x- (la variable x est remplacée par la variable y).
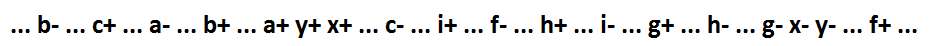
Maintenant x = (f + i + h + g) * y, y = c * b * a + x. Les implicants f + i + h + g et c * b * a comprenant et, respectivement, les fonctions x et y peuvent être fragmentés en composantes minimales tout en conservant une auto-synchronisation.
Un modèle de comportement simplifié (sans parallélisme, choix et signaux multiples) vous permet d'identifier les propriétés naturellement inhérentes aux processus binaires. La synthèse de circuits auto-synchrones dans une base minimale est un phénomène naturel qui ne nécessite aucune conception.