Dans un article précédent, j'ai souligné à quel point le problème de l'utilisation abusive du critère t est répandu dans les publications scientifiques (et cela n'est possible qu'en raison de leur ouverture et des déchets créés lorsqu'ils sont utilisés dans n'importe quel cours, rapports, tâches de formation, etc. - est inconnu) . Pour en discuter, j'ai parlé des bases de l'analyse de la variance et du niveau de signification α fixé par le chercheur lui-même. Mais pour bien comprendre l’ensemble de l’analyse statistique, il est nécessaire de souligner un certain nombre de choses importantes. Et le plus fondamental d'entre eux est le concept d'erreur.
Erreur et application incorrecte: quelle est la différence?
Tout système physique contient une sorte d'erreur, d'inexactitude. Sous la forme la plus diversifiée: la soi-disant tolérance - la différence de taille de différents produits du même type; caractéristique non linéaire - lorsqu'un appareil ou une méthode mesure quelque chose selon une loi bien connue dans certaines limites, puis devient inapplicable; discrétion - lorsque nous sommes techniquement incapables d'assurer une caractéristique de sortie régulière.
Et en même temps, il y a une erreur purement humaine - une mauvaise utilisation des appareils, des instruments, des lois mathématiques. Il existe une différence fondamentale entre l'erreur inhérente au système et l'erreur dans l'application de ce système. Il est important de distinguer et de ne pas confondre entre eux ces deux concepts, appelés le même mot «erreur». Dans cet article, je préfère utiliser le mot «erreur» pour désigner les propriétés du système et «utilisation incorrecte» - pour son utilisation erronée.
Autrement dit, l'erreur de la règle est égale à la tolérance de l'équipement, en mettant des traits sur sa toile. Une erreur dans le sens d'une mauvaise utilisation serait de l'utiliser pour mesurer les détails d'une montre. L'erreur du steelyard y est inscrite et s'élève à environ 50 grammes, et le mauvais usage du steelyard serait de peser un sac de 25 kg dessus, ce qui étire le ressort de la région de la loi de Hooke à la région des déformations plastiques. L'erreur d'un microscope à force atomique provient de sa discrétion - vous ne pouvez pas "toucher" des objets avec une sonde plus petite qu'avec un diamètre d'un atome. Mais il existe de nombreuses façons de les utiliser à mauvais escient ou de mal interpréter les données. Et ainsi de suite.
Alors, quel genre d'erreur cela a-t-il dans les méthodes statistiques? Et cette erreur est précisément le niveau notoire de signification α.
Erreurs du premier et du deuxième type
Une erreur dans l'appareil mathématique des statistiques est son essence probabiliste bayésienne elle-même. Dans le dernier article, j'ai déjà mentionné les méthodes statistiques sur lesquelles reposent: la détermination du niveau de signification α comme la plus grande probabilité admissible de rejeter illégalement l'hypothèse nulle, et le chercheur d'attribuer indépendamment cette valeur au chercheur.
Voyez-vous déjà cette convention? En fait, dans les méthodes de critères, il n'y a pas de rigueur mathématique familière. Les mathématiques fonctionnent sur des caractéristiques probabilistes.
Et voici un autre point où une mauvaise interprétation d'un mot dans un contexte différent est possible. Il faut faire la distinction entre le concept de probabilité et la mise en œuvre réelle d'un événement, exprimé dans la distribution de probabilité. Par exemple, avant de commencer l'une de nos expériences, nous ne savons pas quel type de valeur nous obtiendrons en conséquence. Il y a deux résultats possibles: après avoir fait une certaine valeur du résultat, nous l'obtiendrons vraiment ou non. Il est logique que la probabilité des deux événements soit de 1/2. Mais la courbe gaussienne présentée dans l'article précédent montre
la distribution de probabilité que l'on devine correctement la coïncidence.
Vous pouvez clairement illustrer cela avec un exemple. Lançons deux fois 600 dés - régulier et infidèle. Nous obtenons les résultats suivants:

Avant l'expérience, pour les deux cubes, la perte de n'importe quel visage sera également probable - 1/6. Cependant, après l'expérience, l'essence du cube de triche apparaît, et nous pouvons dire que la densité de probabilité des six qui le tombent est de 90%.
Un autre exemple connu des chimistes, des physiciens et de toute personne intéressée par les effets quantiques est celui des orbitales atomiques. Théoriquement, un électron peut être «étalé» dans l'espace et situé presque n'importe où. Mais dans la pratique, il y aura des domaines dans 90% ou plus des cas. Ces régions de l'espace formées par une surface dont la densité de probabilité de l'électron est de 90% sont des orbitales atomiques classiques sous forme de sphères, d'haltères, etc.
Ainsi, en fixant indépendamment le niveau de signification, nous acceptons délibérément l'erreur décrite dans son nom. Pour cette raison, aucun résultat ne peut être considéré comme «complètement fiable» - nos conclusions statistiques contiendront toujours une probabilité d'échec.
Une erreur formulée en déterminant le niveau de signification α est appelée une
erreur du premier type . Il peut être défini comme une «fausse alarme» ou, plus exactement, un faux résultat positif. En fait, que signifient les mots «rejeter par erreur l'hypothèse nulle»? Cela signifie prendre par erreur les données observées pour des différences significatives entre les deux groupes. Faire un faux diagnostic sur la présence de la maladie, se précipiter pour révéler au monde une nouvelle découverte, qui n'existe pas réellement - ce sont des exemples d'erreurs du premier type.
Mais alors, devrait-il y avoir de faux résultats négatifs? Tout à fait raison, et ils sont appelés
erreurs du deuxième type . Les exemples sont un diagnostic prématuré ou une déception à la suite de l'étude, bien qu'en fait il contienne des données importantes. Les erreurs du deuxième type sont indiquées par la lettre, curieusement, β. Mais ce concept lui-même n'est pas aussi important pour les statistiques que le nombre 1-β. Le nombre 1-β est appelé la
puissance du critère , et comme vous pouvez le deviner, il caractérise la capacité du critère à ne pas manquer un événement significatif.
Cependant, le contenu des méthodes statistiques d'erreurs du premier et du deuxième type n'est pas seulement leur limitation. Le concept même de ces erreurs peut être utilisé directement dans l'analyse statistique. Comment?
Analyse ROC
L'analyse ROC (à partir de la caractéristique de fonctionnement du récepteur) est une méthode pour quantifier l'applicabilité d'un certain attribut à une classification binaire d'objets. En termes simples, nous pouvons trouver un moyen de distinguer les personnes malades des personnes en bonne santé, les chats des chiens, les noirs des blancs, puis vérifier la validité de cette méthode. Regardons à nouveau un exemple.
Laissez-vous être un scientifique légiste en herbe et développez une nouvelle façon de déterminer discrètement et sans équivoque si une personne est un criminel. Vous avez trouvé un signe quantitatif: évaluer les penchants criminels des gens par la fréquence de leur écoute de Mikhail Krug. Mais votre symptôme donnera-t-il des résultats adéquats? Faisons les choses correctement.
Vous aurez besoin de deux groupes de personnes pour valider vos critères: les citoyens ordinaires et les criminels. En effet, supposons que la durée moyenne annuelle d'écoute de Mikhail Krug soit différente (voir la figure):
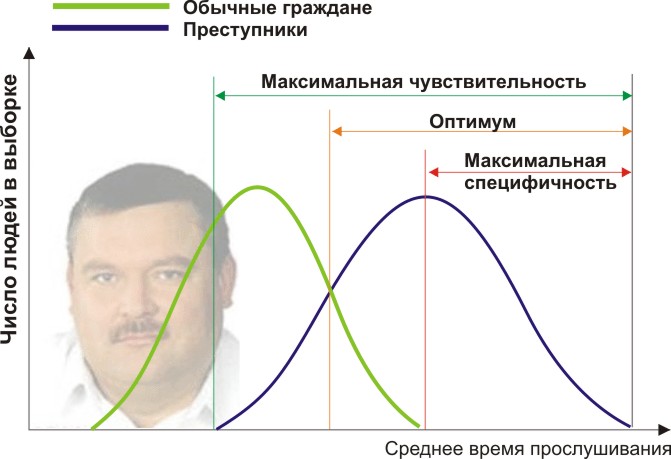
On voit ici que par le signe quantitatif du temps d'écoute, nos échantillons se croisent. Quelqu'un écoute le Cercle spontanément à la radio sans commettre de délits, et quelqu'un viole la loi en écoutant d'autres musiques ou même en étant sourd. Quelles conditions aux limites avons-nous? L'analyse ROC introduit les concepts de sélectivité (sensibilité) et de spécificité. La sensibilité est définie comme la capacité à identifier tous les points d'intérêt pour nous (dans cet exemple, les criminels), et la spécificité - pour ne rien capturer de faux positifs (pour ne pas mettre les habitants ordinaires en suspicion). Nous pouvons définir un trait quantitatif critique qui sépare certains des autres (orange), allant de la sensibilité maximale (vert) à la spécificité maximale (rouge).
Regardons le schéma suivant:

En décalant la valeur de notre attribut, nous modifions le rapport des résultats faux positifs et faux négatifs (l'aire sous les courbes). De la même manière, nous pouvons définir Sensibilité = Position. Res-t / (Res-t positif + faux négatif. Res-t) et spécificité = Neg. Res-t / (Res-t négatif + faux positif. Res-t).
Mais le plus important, nous pouvons évaluer le rapport des résultats positifs aux faux positifs sur toute la plage de valeurs de notre attribut quantitatif, qui est notre courbe ROC souhaitée (voir figure):

Et comment pouvons-nous comprendre à partir de ce graphique à quel point notre attribut est bon? Très simple, calculez l'aire sous la courbe (AUC, aire sous la courbe). La ligne pointillée (0,0; 1,1) signifie la coïncidence complète des deux échantillons et un critère complètement dénué de sens (l'aire sous la courbe est 0,5 du carré entier). Mais la convexité de la courbe ROC indique simplement la perfection du critère. Si nous parvenons à trouver un critère tel que les échantillons ne se coupent pas du tout, alors la zone sous la courbe occupera tout le graphique. En général, le caractère est considéré comme bon, permettant à l'un de séparer de manière fiable un échantillon d'un autre si l'ASC> 0,75-0,8.
Avec cette analyse, vous pouvez résoudre une variété de problèmes. Ayant décidé que trop de femmes au foyer sont soupçonnées à cause de Michael Krug, et en outre, les récidivistes dangereux qui écoutent Noggano sont manqués, vous pouvez rejeter ce critère et en développer un autre.
Ayant émergé comme un moyen de traiter les signaux radio et d'identifier «ami ou ennemi» après une attaque sur Pearl Harbor (d'où le nom étrange pour les caractéristiques du récepteur), l'analyse ROC a été largement utilisée dans les statistiques biomédicales pour analyser, valider, créer et caractériser des panneaux de biomarqueurs etc. Il est flexible à utiliser s'il est basé sur une logique sonore. Par exemple, vous pouvez développer des indications pour l'examen médical des patients de base retraités en appliquant un critère très spécifique, en augmentant l'efficacité de la détection des maladies cardiaques et en ne surchargeant pas les médecins de patients inutiles. Et lors d'une épidémie dangereuse d'un virus jusque-là inconnu, au contraire, vous pouvez trouver un critère hautement sélectif pour que personne d'autre n'échappe littéralement à la vaccination.
Nous avons rencontré des erreurs des deux types et leur visibilité dans la description des critères validés. Maintenant, en partant de ces fondements logiques, nous pouvons détruire une série de fausses descriptions stéréotypées des résultats. Certaines formulations incorrectes capturent nos esprits, souvent confondues par leurs mots et concepts similaires, et aussi en raison du très peu d'attention prêté à une interprétation incorrecte. Cela devra peut-être être écrit séparément.