Algorithme de triangulation de Delaunay par la méthode des lignes de balayage

Bonjour!

Dans cet article, je décrirai en détail l'algorithme que j'ai obtenu grâce à l'idée de «balayer la droite» pour construire la triangulation de Delaunay sur un plan. Il contient plusieurs idées que je n'ai jamais rencontrées en lisant des articles sur la triangulation.
Peut-être que quelqu'un les trouvera également inhabituels. Je vais essayer de tout faire dans la meilleure tradition et d'inclure les choses suivantes dans l'histoire: une description des structures de données utilisées, une description des étapes de l'algorithme, une preuve de correction, des estimations de temps, ainsi qu'une comparaison avec un algorithme itératif utilisant l'arbre kD.

Définitions et énoncé du problème

Triangulation

Ils disent que la triangulation est spécifiée sur l'ensemble des points du plan si certaines paires de points sont reliées par une arête, toute face finie dans le graphique résultant forme un triangle, les arêtes ne se coupent pas et le graphe est maximal en nombre d'arêtes.

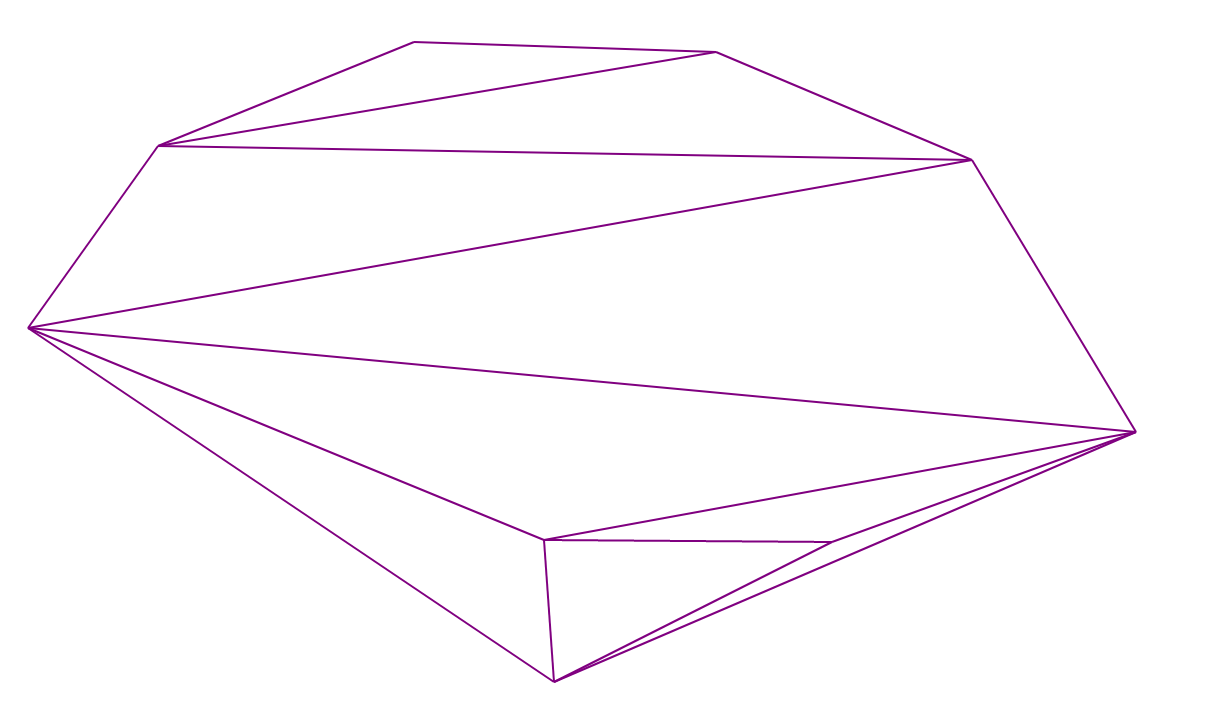
Triangulation de Delaunay

Une triangulation de Delaunay est une triangulation dans laquelle, pour tout triangle, il est vrai qu'il n'y a pas de points de l'ensemble d'origine à l'intérieur du cercle circonscrit autour de lui.

Remarque : pour un ensemble donné de points dans lesquels aucun 4 points ne se trouve sur le même cercle, il y a exactement une triangulation de Delaunay.

La condition Delaunay

Soit une triangulation donnée sur l'ensemble des points. Nous disons qu'un certain sous-ensemble de points satisfait la condition de Delaunay si la triangulation délimitée sur ce sous-ensemble est pour lui la triangulation de Delaunay.

Critère de triangulation de Delaunay

Le respect de la condition de Delaunay pour tous les points formant un quadrilatère dans une triangulation équivaut au fait que cette triangulation est une triangulation de Delaunay.

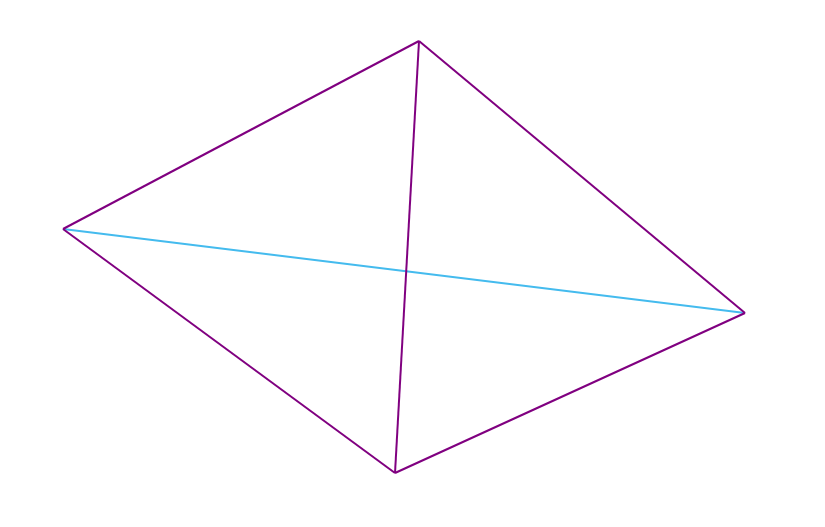
Remarque : pour les quadrangles non convexes, la condition de Delaunay est toujours remplie, et pour les quadrangles convexes (dont les sommets ne se trouvent pas sur le même cercle), il y a exactement 2 triangulations possibles (dont l'une est la triangulation de Delaunay).

La tâche consiste à construire une triangulation de Delaunay pour un ensemble de points donné.

Description de l'algorithme

Points visibles et bords visibles

Soit une coque convexe minimale (ci-après, MBO) d'un ensemble fini de points (bords reliant certains des points de sorte qu'ils forment un polygone contenant tous les points de l'ensemble) et un point A situé à l'extérieur de la coque. Ensuite, le point de l'avion est appelé visible pour le point A, si le segment le reliant au point A ne coupe pas le MBO.

Un bord MBO est appelé visible pour le point A si ses extrémités sont visibles pour A.

Dans l'image suivante, les bords visibles pour le point rouge sont marqués en rouge:

Remarque : le contour de triangulation Delaunay est le MBO des points sur lesquels il est construit.

Remarque 2 : dans l'algorithme, les arêtes visibles pour le point ajouté A forment une chaîne, c'est-à-dire plusieurs arêtes MBO d'affilée

Stocker la triangulation en mémoire

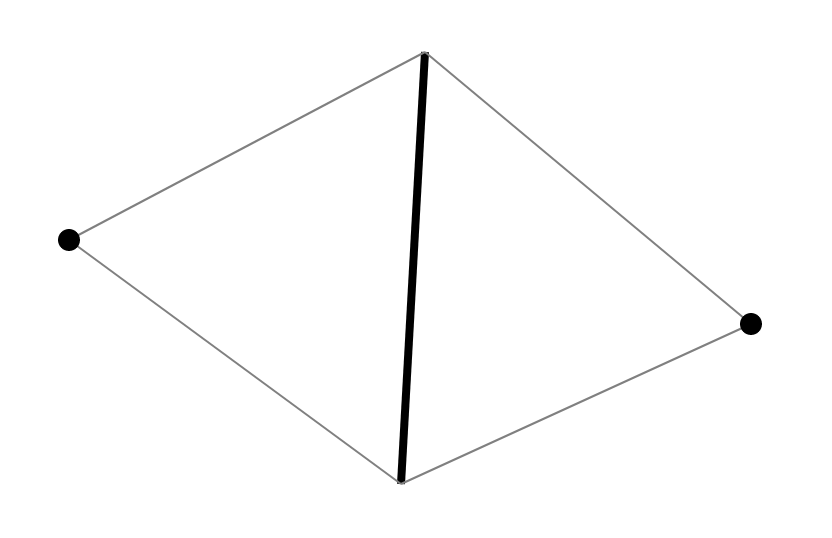
Il existe certaines méthodes standard qui sont bien décrites dans le livre de Skvortsov [1]. En raison des spécificités de l'algorithme, je proposerai ma propre version. Puisque nous voulons vérifier les 4 gons pour l'état de Delaunay, nous considérons leur structure. Chaque quadrangle en triangulation est composé de 2 triangles ayant un bord commun. Chaque arête a exactement 2 triangles adjacents. Ainsi, chaque quadrangle en triangulation est généré par une arête et deux sommets opposés à l'arête dans des triangles adjacents.
Puisque deux triangles et leur adjacence sont restaurés le long du bord et de deux sommets, nous pouvons restaurer la triangulation pour toutes ces structures. En conséquence, il est proposé de stocker une arête avec deux sommets dans l'ensemble et d'effectuer une recherche le long de l'arête (une paire ordonnée de sommets).

Algorithme

L'idée de la ligne de balayage est que tous les points sont triés dans une direction, puis traités à leur tour.

1. Trier tous les points le long d'une ligne droite (pour plus de simplicité, par coordonnées $$$x$)
2. Nous construisons un triangle sur les 3 premiers points.
   
   De plus, pour chaque point suivant, nous effectuerons des étapes qui préservent l'invariant qu'il existe une triangulation de Delaunay pour les points déjà ajoutés et, en conséquence, un MBO pour eux.
3. Ajoutez les triangles formés par les bords visibles et le point lui-même (c'est-à-dire, ajoutez les bords du point en question à toutes les extrémités des bords visibles).
4. On vérifie sur la condition de Delaunay tous les quadrangles générés par les bords visibles. Si la condition n'est pas remplie quelque part, nous reconstruisons la triangulation dans le quadrangle (je me souviens qu'il n'y en a que deux) et exécutons récursivement la vérification des quadrangles générés par les bords du quadrangle actuel (car ce n'est qu'après eux que la condition Delaunay pourrait être violée).

Remarque : à l'étape (4) lors d'un démarrage récursif, vous ne pouvez pas vérifier les quadrangles générés par les arêtes provenant du point considéré à cette itération (il y en a toujours deux sur quatre). Le plus souvent, ils seront non convexes, car pour la convexe la preuve est purement géométrique, je laisse le soin au lecteur. De plus, nous supposons que seulement 2 démarrages récursifs sont effectués pour chaque reconstruction.

Vérification d'une condition Delaunay

Les moyens de tester les quadrangles pour la condition de Delaunay peuvent être trouvés dans le même livre [1]. Je note seulement que lors du choix d'une méthode avec des fonctions trigonométriques à partir de là, avec une implémentation inexacte, des valeurs négatives de sinus peuvent être obtenues, il est logique de les prendre modulo.

Rechercher les bords visibles

Reste à comprendre comment trouver efficacement les bords visibles. Notez que le point ajouté S précédent se trouve dans le MBO à l'itération actuelle, car il a la plus grande coordonnée $$$x$et est également visible pour le point actuel. Ensuite, notant que les extrémités des bords visibles forment une chaîne continue de points visibles, nous pouvons aller du point S dans les deux directions le long du MBO et collecter les bords pendant qu'ils sont visibles (la visibilité du bord est vérifiée à l'aide du produit vectoriel). Ainsi, il est pratique de stocker le MBO en tant que liste doublement connectée, à chaque itération, supprimant les bords visibles et en ajoutant 2 nouveaux à partir du point considéré.

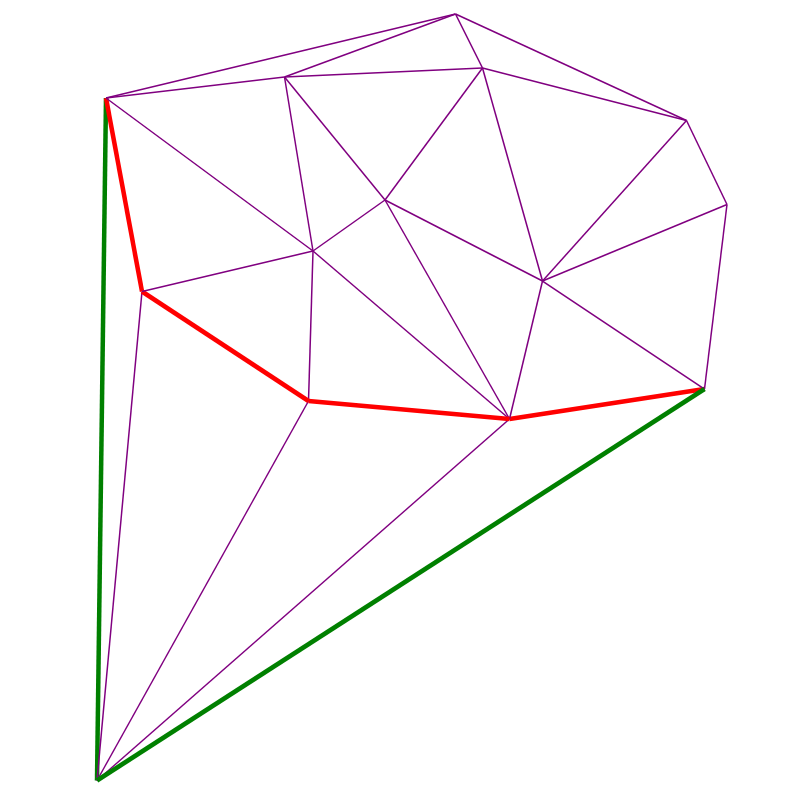
Visualisation d'algorithme

Deux points rouges - ajoutés et précédents. Des bords rouges à chaque instant constituent la pile de récursivité de l'étape (4):

Exactitude de l'algorithme

Pour prouver l'exactitude de l'algorithme, il suffit de prouver la conservation de l'invariant aux étapes (3) et (4).

Étape (3)

Après l'étape (3), évidemment, nous obtenons une triangulation de l'ensemble actuel de points.

Étape (4)

Dans le processus de l'étape (4), tous les quadrangles qui ne satisfont pas à la condition de Delaunay sont dans la pile de récursivité (découle de la description), ce qui signifie qu'à la fin de l'étape (4), tous les quadrangles satisfont à la condition de Delaunay, c'est-à-dire que la triangulation de Delaunay est réellement construite. Il reste alors à prouver que le processus de l'étape (4) se terminera un jour. Cela découle du fait que toutes les arêtes ajoutées lors de la reconstruction proviennent du sommet actuel en question (c'est-à-dire à l'étape $$$k$il n'y a pas plus de $$$k-1$) et du fait qu'après avoir ajouté ces arêtes, nous ne prendrons pas en compte les quadrangles générés par celles-ci (voir la remarque précédente), ce qui signifie que nous n'en ajouterons pas plus d'une fois.

Complexité temporelle

En moyenne, l'algorithme fonctionne assez bien sur des distributions uniformes et normales (les résultats sont présentés dans le tableau ci-dessous). On suppose que son temps de travail est $$$O (NlogN)$. Dans le pire des cas, une évaluation a lieu $$$O (N ^ 2)$.

Examinons le temps de travail en plusieurs parties et comprenons lequel a le plus d'impact sur le temps total:

Trier par direction

Pour le tri, nous utiliserons l'estimation $$$O (NlogN)$.

Rechercher les bords visibles

Tout d'abord, nous montrons que le temps total passé à rechercher des bords visibles est $$$O (N)$. Notez qu'à chaque itération, nous trouvons toutes les arêtes visibles et 2 autres (la première non visible) en temps linéaire. À l'étape (3), nous ajoutons de nouveaux 2 bords au MBO. Ainsi, au total, pas plus de $$$2N$par conséquent, et diverses côtes visibles ne seront plus $$$2N$. Nous trouverons également $$$2N$bords non visibles. Ainsi, au total, il n'y a plus $$$4N$côtes qui correspondent au temps $$$O (N)$.

Construire de nouveaux triangles

Le temps total pour construire des triangles de l'étape (3) avec des bords visibles déjà trouvés est évidemment $$$O (N)$.

Reconstruire la triangulation

Il reste à traiter l'étape (4). Tout d'abord, notez que vérifier la condition de Delaunay et la reconstruire si elle n'est pas remplie sont des actions assez coûteuses (bien qu'elles fonctionnent pour $$$O (1)$) Seule la vérification de la condition de Delaunay peut prendre environ 28 opérations arithmétiques. Examinons le nombre moyen de reconstructions au cours de cette étape. Les résultats pratiques de certaines distributions sont donnés ci-dessous. Pour eux, je veux vraiment dire que le nombre moyen de réarrangements augmente avec une vitesse logarithmique, mais laissons cela comme hypothèse.

Ici, je tiens également à noter que le nombre moyen de réarrangements par point peut varier considérablement en fonction de la direction dans laquelle le tri est effectué. Ainsi, pour un million uniformément réparti sur un long rectangle bas avec un rapport d'aspect de 100000: 1, ce nombre varie de 1,2 à 24 (ces valeurs sont obtenues lors du tri des données horizontalement et verticalement, respectivement). Par conséquent, je vois l'intérêt de choisir la direction de tri de manière arbitraire (dans cet exemple, avec une sélection arbitraire, en moyenne environ 2 reconstructions ont été obtenues) ou de la sélectionner manuellement si les données sont connues à l'avance.

Ainsi, la durée principale du programme passe généralement à l'étape (4). S'il s'exécute rapidement, il est logique de penser à accélérer le tri.

Pire cas

Pire cas sur $$$k$e itération se produit $$$k-1$l'appel récursif à l'étape (4), c'est-à-dire en sommant sur tout i, nous obtenons le comportement asymptotique dans le pire des cas $$$O (N ^ 2)$. L'image suivante illustre un bel exemple sur lequel le programme peut fonctionner pendant longtemps (1100 reconstructions en moyenne lors de l'ajout d'un nouveau point avec une entrée de 10 000 points).

Comparaison avec un algorithme itératif pour construire une triangulation de Delaunay en utilisant kD-tree

Description de l'algorithme itératif

Je décrirai brièvement l'algorithme ci-dessus. Lorsque le point suivant arrive, nous utilisons l'arbre kD (je vous conseille de le lire quelque part, si vous ne le savez pas), nous trouvons un triangle qui est déjà assez proche de lui. Puis, en contournant en profondeur, nous recherchons un triangle dans lequel le point lui-même tombe. Nous étendons les bords aux sommets du triangle trouvé et effectuons réellement l'étape (4) de notre algorithme pour les nouveaux quadrangles. Comme le point peut être en dehors de la triangulation, pour simplifier, il est proposé de couvrir tous les points avec un grand triangle (pour le construire à l'avance), cela résoudra le problème.

Similitude des algorithmes

En fait, si des points sont ajoutés dans l'ordre triés par direction, notre algorithme fonctionne en fait de la même manière que l'itératif, sauf que le nombre de réarrangements est inférieur. L'animation suivante le démontre parfaitement. Sur celui-ci, des points ont été ajoutés de droite à gauche, et ils sont tous couverts par un grand triangle, qui est ensuite supprimé.

Différences d'algorithme

Dans un algorithme itératif, la localisation d'un point (recherche du triangle souhaité) se produit en moyenne sur $$$O (logN)$, sur les distributions ci-dessus, en moyenne, 3 réarrangements se produisent (comme indiqué dans [1]) sous la condition d'un ordre arbitraire de fourniture de points. Ainsi, la ligne de balayage gagne le temps de l'algorithme itératif en localisation, mais le perd en reconstruction (ce qui, je le rappelle, est assez difficile). De plus, l'algorithme itératif fonctionne en ligne, ce qui est également sa caractéristique distinctive.

Conclusion

Ici, je montre juste quelques triangulations intéressantes résultant du fonctionnement de l'algorithme.

Beau motif

Distribution normale, 1000 points

Distribution uniforme, 1000 points

Triangulation basée sur l'emplacement de toutes les villes de Russie

Ici vous pouvez voir un exemple de mon code pour cet algorithme:
github.com/Vemmy124/Delaunay-Triangulation-Algorithm

Merci de votre attention!

Littérature

[1] Skvortsov A.V. Triangulation de Delaunay et son application. - Tomsk: maison d'édition Tom. Université, 2002 .-- 128 p. ISBN 5-7511-1501-5