Cet article classique détaille les façons les plus populaires de créer et de parcourir des labyrinthes. L'article est divisé en quatre parties: classification, algorithmes de génération, algorithmes de résolution de labyrinthes et autres opérations avec des labyrinthes.Classification du labyrinthe
Les labyrinthes dans leur ensemble (et donc les algorithmes pour les créer) peuvent être divisés en sept classifications différentes: dimension, hyperdimension, topologie, tessellation, routage, texture et priorité. Le labyrinthe peut utiliser un élément de chaque classe dans n'importe quelle combinaison.
Dimension: la classe de dimension détermine essentiellement le nombre de dimensions dans l'espace que le labyrinthe remplit. Les types suivants sont disponibles:

Deux dimensions : la plupart des labyrinthes, papier et réel, ont cette dimension, c'est-à-dire que nous pouvons toujours afficher le plan du labyrinthe sur une feuille de papier et le déplacer sans traverser d'autres couloirs du labyrinthe.- En trois dimensions : le labyrinthe en trois dimensions a plusieurs niveaux; en elle (au moins dans la version orthogonale), les passages peuvent descendre et monter, en plus des quatre points cardinaux. Un labyrinthe 3D est souvent visualisé comme un tableau de niveaux 2D avec des escaliers de haut en bas.
Dimensions supérieures : vous pouvez créer des labyrinthes à quatre dimensions et encore plus des labyrinthes multidimensionnels. Parfois, ils sont visualisés comme des labyrinthes 3D avec des «portails» menant à travers la quatrième dimension, par exemple, des portails vers le «passé» et le «futur».
Entrelacement : labyrinthes avec entrelacement - ce sont essentiellement des labyrinthes bidimensionnels (ou plutôt 2,5 dimensions), dans lesquels, cependant, les passages peuvent se chevaucher. Lors de l'affichage, il est généralement assez évident où se trouvent les impasses et comment un passage est au-dessus de l'autre. Des labyrinthes du monde réel, dans lesquels se trouvent des ponts reliant une partie du labyrinthe à une autre, s'entrelacent partiellement.
Hyperdimension: la classification selon l'hyperdimension correspond à la dimension d'un objet se déplaçant dans un labyrinthe, et non au labyrinthe lui-même. Les types suivants sont disponibles:

Non-hyperlabyrinthes : presque tous les labyrinthes, même ceux créés en haute dimensionnalité ou avec des règles spéciales, sont généralement des non-hyperlabyrinthes. En eux, nous travaillons avec un point ou un petit objet, par exemple, une balle ou le joueur lui-même, qui se déplace d'un point à un autre, et l'itinéraire pavé forme une ligne. À chaque point, il existe un nombre de choix facilement dénombrable.- Hyperlabyrinthes: les hyperlabyrinthes sont des labyrinthes dans lesquels l'objet à résoudre n'est pas seulement un point. Un hyperlabyrinthe standard (ou hyperlabyrinthe de premier ordre) consiste en une ligne qui forme une surface lors du déplacement le long d'un chemin. L'hyperlabyrinthe ne peut exister qu'en 3D ou dans un milieu de plus grande dimension, et l'entrée de l'hyperlabyrinthe n'est souvent pas un point, mais une ligne. L'hyperlabyrinthe est fondamentalement différent, car il est nécessaire de prendre en compte et de travailler simultanément avec plusieurs parties le long de la ligne, et à tout moment, il existe un nombre presque infini d'états et d'options pour ce qui peut être fait avec la ligne. La ligne de solution est infinie, ou ses extrémités sont en dehors de l'hyperlabyrinthe pour éviter que la ligne ne soit compressée en un point, car dans ce cas, elle peut être considérée comme non hyperlabyrinthe.
- Hyper-hyperlabyrinthe: les hyperlabyrinthes peuvent avoir une dimension arbitrairement élevée. L'hyper-hyperlabyrinthe (ou hyperlabyrinthe de second ordre) augmente à nouveau la dimension de l'objet à résoudre. Ici, l'objet à résoudre est un plan qui, en se déplaçant le long du chemin, forme une figure tridimensionnelle. L'hyper-hyperlabyrinthe ne peut exister que dans un environnement dimensionnel 4D ou supérieur.
Topologie: la classe de topologie décrit la géométrie de l'espace du labyrinthe dans lequel il existe dans son ensemble. Les types suivants sont disponibles:

Normal : il s'agit du labyrinthe standard dans l'espace euclidien.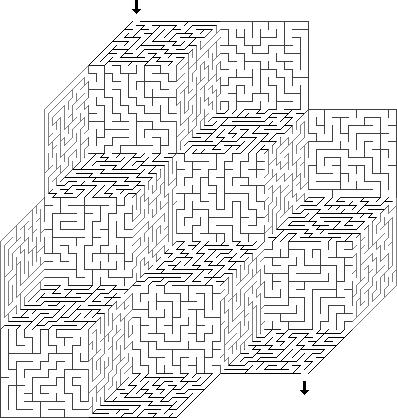
Planair : Le terme «planair» décrit tout labyrinthe avec une topologie inhabituelle. Cela signifie généralement que les bords du labyrinthe sont connectés de manière intéressante. Exemples: labyrinthes à la surface d'un cube, labyrinthes à la surface d'une bande Mobius et labyrinthes équivalents à ceux d'un tore où les côtés gauche et droit, supérieur et inférieur sont reliés par paires.
Tessellation: une classification de la géométrie des cellules individuelles qui composent le labyrinthe. Types existants:

Orthogonale : Il s'agit d'une grille rectangulaire standard dans laquelle les cellules ont des passages qui se coupent à angle droit. Dans le contexte de la tessellation, ils peuvent également être appelés labyrinthes gamma.
Delta : les labyrinthes Delta se composent de triangles connectés, et chaque cellule peut avoir jusqu'à trois passages qui lui sont connectés.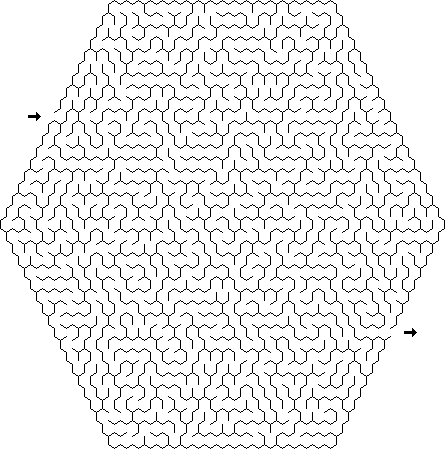
Sigma : les labyrinthes Sigma sont constitués d'hexagones connectés; chaque cellule peut avoir jusqu'à six passes.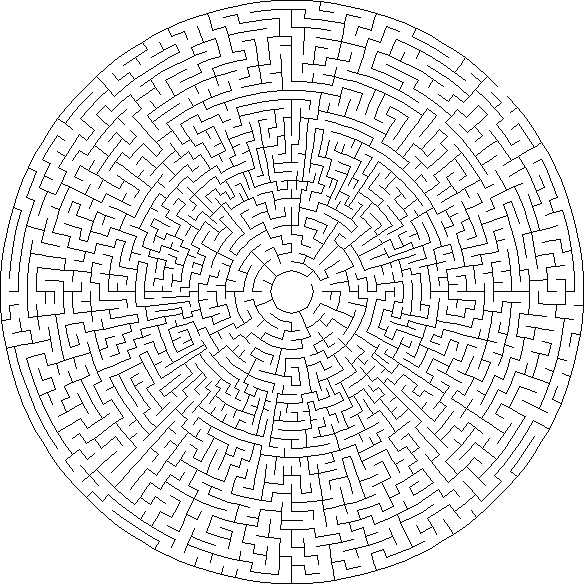
Thêta : les labyrinthes thêta sont constitués de cercles concentriques de passages dont le début ou la fin est au centre et l'autre sur le bord extérieur. Les cellules ont généralement quatre chemins de connexion possibles, mais il peut y en avoir plus en raison du plus grand nombre de cellules dans les anneaux externes des passages.
Epsilon : les labyrinthes d'Epsilon sont constitués d'octogones ou de carrés connectés, chaque cellule en eux peut avoir jusqu'à huit ou quatre passes.
Zeta : Le labyrinthe zeta est situé sur une grille rectangulaire, seulement en plus des passages horizontaux et verticaux, les passages diagonaux sont autorisés à un angle de 45 degrés.
Oméga : le terme oméga fait référence à presque tous les labyrinthes à pavage constant non orthogonal. Les labyrinthes delta, sigma, thêta et ipsilon sont de ce type, comme de nombreux autres schémas auxquels vous pouvez penser, par exemple, un labyrinthe composé de paires de triangles rectangles.
Fissure : Un labyrinthe de fissures est un labyrinthe amorphe sans pavage constant, dans lequel les murs et les allées sont situés à des angles aléatoires.
Fractale : Un labyrinthe fractal est un labyrinthe composé de labyrinthes plus petits. Un labyrinthe fractal à partir de cellules imbriquées est un labyrinthe dans chaque cellule dont d'autres labyrinthes sont placés, et ce processus peut être répété plusieurs fois. Un labyrinthe fractal infiniment récursif est une véritable fractale dans laquelle le contenu du labyrinthe se réplique, créant un labyrinthe essentiellement infiniment grand.
Routage: La classification par routage est probablement l'aspect le plus intéressant dans la génération de labyrinthes. From est associé à des types de passes dans la géométrie définie dans les catégories décrites ci-dessus.

Idéal : «idéal» est un labyrinthe sans boucles ni circuits fermés et sans zones inaccessibles. Il est également appelé un labyrinthe simplement connecté. De chaque point, il y a exactement un chemin vers tout autre point. Labyrinth n'a qu'une seule solution. Du point de vue de la programmation, un tel labyrinthe peut être décrit comme un arbre, un ensemble de connexion de cellules ou de sommets.
Tressé : tressé signifie qu'il n'y a pas d'impasse dans le labyrinthe. Il est également appelé le labyrinthe de labyrinthe purement connecté. Dans un tel labyrinthe, on utilise des passages fermés et revenant les uns aux autres (d'où le nom «osier»), ils leur font passer plus de temps à tourner en rond au lieu de se retrouver dans des impasses. Un labyrinthe tissé de qualité peut être beaucoup plus compliqué qu'un labyrinthe idéal de la même taille.
Single-route (Unicursal) : single- route signifie un labyrinthe sans fourches. Le labyrinthe à sens unique contient un long passage sinueux qui change de direction dans tout le labyrinthe. Ce n'est pas très compliqué, seulement si vous ne faites pas accidentellement demi-tour et ne revenez pas au début.
Clairsemé: un labyrinthe clairsemé ne traverse pas chaque cellule, c'est-à-dire que certains d'entre eux ne sont pas créés. Cela implique la présence de zones inaccessibles, c'est-à-dire en quelque sorte l'opposé du labyrinthe en osier. Un concept similaire peut être appliqué lors de l'ajout de murs, de sorte que vous pouvez obtenir un labyrinthe inégal avec de larges allées et des pièces.- Partiellement en osier: Labyrinthe partiellement en osier est un labyrinthe mixte qui a à la fois des boucles et des impasses. Le mot «osier» peut être utilisé pour une évaluation quantitative, c'est-à-dire qu'un «labyrinthe solide» est un labyrinthe avec de nombreuses boucles ou des murs rétractés, et il n'y en a que quelques-uns dans le «labyrinthe faiblement tissé».
Texture: la classification de la
texture décrit le style des passes avec un routage et une géométrie différents. La texture n'est pas seulement des paramètres qui peuvent être activés ou désactivés. Voici quelques exemples de variables:

Biais : dans un labyrinthe avec des passages décalés, les passages droits ont tendance à aller plus dans un sens que dans les autres. Par exemple, dans un labyrinthe à fort déplacement horizontal, nous aurons de longs passages de gauche à droite, et seulement de courts passages de haut en bas les reliant. Un tel labyrinthe est généralement plus difficile à passer «à travers les fibres».
Overflight : la métrique Overflight détermine combien de temps les couloirs prendront avant que les virages forcés n'apparaissent. Dans un labyrinthe de faible envergure, il n'y aura pas de passages rectilignes de plus de trois ou quatre cellules, et cela aura l'air très aléatoire. Dans un labyrinthe à grande portée, le labyrinthe aura un grand pourcentage de passes longues, ce qui lui donnera l'apparence d'une micropuce.
Élitisme: l'indicateur «élite» du labyrinthe détermine la longueur de la solution par rapport à la taille du labyrinthe. Les labyrinthes d'élite ont généralement une solution courte et directe, et dans les labyrinthes non élites, la solution passe sur une grande partie de la zone du labyrinthe. Un labyrinthe d'élite de haute qualité peut être beaucoup plus compliqué qu'un labyrinthe non d'élite.
Symétrie : un labyrinthe symétrique a des passages symétriques, par exemple, dans la symétrie de rotation par rapport au centre, ou réfléchi le long des axes horizontal ou vertical. Le labyrinthe peut être partiellement ou complètement symétrique et peut répéter le motif un certain nombre de fois.
Homogénéité: un algorithme homogène génère tous les labyrinthes possibles avec une probabilité égale. Un labyrinthe peut être qualifié de texture homogène s'il ressemble à un labyrinthe typique généré par un algorithme homogène. Un algorithme hétérogène peut théoriquement également générer tous les labyrinthes possibles dans n'importe quel espace, mais pas avec une probabilité égale. L'hétérogénéité peut aller encore plus loin - il peut y avoir des labyrinthes que l'algorithme ne générera jamais.- Débit de la rivière: La caractéristique de «débit» signifie que lors de la création d'un labyrinthe, l'algorithme recherchera et nettoiera les cellules (ou parois) voisines de la cellule actuelle, c'est-à-dire qu'il coulera (d'où le terme de «fluidité») dans les parties encore non créées du labyrinthe, comme l'eau. Dans un labyrinthe idéal avec un débit plus faible, il y aura généralement de nombreuses impasses courtes, et dans un labyrinthe plus «fluide», il y aura moins d'impasses, mais elles seront plus longues.
Priorité: cette classification montre que les processus de création de labyrinthes peuvent être divisés en deux types principaux: l'ajout de murs et la sculpture de passages. Habituellement, lors de la génération de cela, cela se résume uniquement à la différence dans les algorithmes, et non à des différences notables dans les labyrinthes, mais il est toujours utile d'en tenir compte. Le même labyrinthe est souvent généré dans les deux sens:
- Ajout de murs: les algorithmes pour lesquels les murs sont prioritaires commencent par une zone vide (ou une bordure externe), ajoutant des murs dans le processus. Dans le monde réel, de vrais labyrinthes composés de haies, de plafonds ou de murs en bois ajoutent définitivement des murs.
- Couper les allées: les algorithmes dont la priorité est aux allées commencent par un bloc solide et coupent des passages dans celui-ci au cours du processus. Dans le monde réel, ces labyrinthes sont des tunnels miniers ou des labyrinthes à l'intérieur des tuyaux.

Modèle: bien sûr, les labyrinthes peuvent simultanément couper des passages et ajouter des murs; certains algorithmes informatiques le font. Un modèle de labyrinthe est une image graphique qui n'est pas un labyrinthe qui, au moindre nombre d'étapes, se transforme en véritable labyrinthe, mais conserve la texture du modèle graphique d'origine. Les styles de labyrinthe complexes, tels que les spirales qui se croisent, sont plus faciles à implémenter en tant que modèles dans un ordinateur, plutôt que d'essayer de créer le bon labyrinthe tout en préservant son style.
Autre: ce qui précède n'est en aucun cas une liste exhaustive de toutes les classes ou éléments possibles au sein de chaque classe. Ce ne sont que ces types de labyrinthes que j'ai créés moi-même. Notez que presque tous les types de labyrinthe, y compris les labyrinthes avec des règles spéciales, peuvent être exprimés sous forme de graphique dirigé dans lequel il y aura un nombre fini d'états et un nombre fini de choix dans chaque état, et cela s'appelle l'
équivalence des labyrinthes . Voici quelques autres classifications et types de labyrinthes:

Orientation : sur certains passages, vous ne pouvez vous déplacer que dans une seule direction. Du point de vue de la programmation, un tel labyrinthe sera décrit par un graphe orienté, contrairement à un graphe non orienté décrivant tous les autres types.
Segmentation : le labyrinthe peut avoir différentes parties correspondant à différentes classes.
Labyrinthes de longueur infinie: nous pouvons créer un labyrinthe infiniment long (un nombre fini de colonnes et un nombre quelconque de lignes), mais en même temps ne stocker qu'une partie du labyrinthe en mémoire, "faire défiler" d'une extrémité à l'autre et détruire les lignes précédentes lors de la création de la suivante. Un exemple est une version modifiée de l'algorithme Hunt and Kill. On peut imaginer un labyrinthe potentiellement sans fin sous la forme d'un long film composé d'images individuelles. Seules deux trames consécutives sont stockées en mémoire à la fois. Exécutons l'algorithme Hunt and Kill, bien qu'il crée un biais sujet au cadre supérieur, il se termine donc en premier. Une fois terminé, le cadre n'est plus nécessaire, vous pouvez l'imprimer ou faire autre chose avec. Quoi qu'il en soit, jetez-le, faites du cadre inférieur partiellement créé un nouveau cadre supérieur et effacez le nouveau cadre inférieur. Répétez le processus jusqu'à ce que nous décidions d'arrêter, puis attendez que Hunt And Kill termine les deux images. La seule limitation est que le labyrinthe n'aura jamais de chemin se ramifiant vers l'entrée sur une longueur de plus de deux images. La façon la plus simple de créer un labyrinthe sans fin est l'algorithme Eller ou l'algorithme Sidewinder, car ils créent déjà des labyrinthes une ligne à la fois, vous pouvez donc simplement les laisser ajouter sans cesse des lignes au labyrinthe.
Labyrinthes fractals virtuels : le virtuel est un labyrinthe dans lequel tout le labyrinthe n'est pas stocké en mémoire en même temps. Par exemple, il ne peut stocker qu'une partie des passages 100x100 près de votre emplacement dans une simulation où vous vous promenez dans un grand labyrinthe. L'extension des labyrinthes fractals imbriqués peut être utilisée pour créer d'énormes labyrinthes virtuels, par exemple, un milliard par milliard de passes. Si nous construisions une véritable copie du labyrinthe d'un milliard par milliard de passes (avec une distance de six pieds entre les passages), cela remplirait la surface de la Terre plus de 6 000 fois! Considérez un labyrinthe de 10 9 à 10 9 passes, ou un labyrinthe fermé avec seulement 9 niveaux. Si nous voulons avoir au moins une partie 100x100 autour de nous, alors il nous suffit de créer au niveau le plus bas un sous-labyrinthe de 100x100 passes et sept labyrinthes 10x10 dans lesquels il est intégré afin de savoir exactement où se trouvent les murs dans la partie 100x100. (En fait, il vaut mieux avoir quatre pièces adjacentes de 100 x 100, formant un carré au cas où vous seriez près du bord ou du coin de la pièce, mais le même concept s'applique ici.) Pour garantir que le labyrinthe est constant et inchangé lors du déplacement, nous avons une formule, définir un nombre de graines aléatoire pour chaque coordonnée à chaque niveau d'imbrication. Les labyrinthes fractals virtuels sont similaires à la fractale Mandelbrot, dont les images existent virtuellement, et nous devons visiter une certaine coordonnée à un grossissement assez élevé. pour qu'il apparaisse.
Algorithmes de labyrinthe
Voici une liste d'algorithmes généralisés pour créer les différentes classes de labyrinthes décrites ci-dessus:

Idéal : pour créer un labyrinthe idéal standard, il est généralement nécessaire de le «cultiver», en garantissant l'absence de boucles et de zones isolées. Nous partons du mur extérieur et ajoutons au hasard un fragment du mur qui le touche. Nous continuons d'ajouter au hasard des segments de mur au labyrinthe, mais vérifions que chaque nouveau segment touche une extrémité du mur existant et que son autre extrémité se trouve dans la partie non créée du labyrinthe. Si vous ajoutez un segment de mur, dont les deux extrémités sont séparées du reste du labyrinthe, cela créera un mur non connecté avec une boucle autour de lui, et si vous ajoutez un segment, dont les deux extrémités touchent le labyrinthe, cela créera une zone inaccessible. Il s'agit d'une méthode pour ajouter des murs; elle est presque analogue à la découpe de passages, dans lesquels des parties des passages sont coupées de sorte qu'une seule extrémité touche la passe existante.
: , , . : (1) , (2) , , -«», (3) , , , (4) , , (3) , , .
: — , , , , . U- , , , , . . , : , , , . , . , .
: , . , , . - , , , , .- 3D : , , , . - .

: , , . ( ): , , , . , . , ; , . , , .
Crack : Crack- , , . , , , «» . , , . , - . , , ; . , .
: «» , , . , - : (1) , . (2) , , , , , (.. ). (3) , , . , .
: — 3D-, -, , . 3D- , , . , , . , . , ( ), , , .
Planair : Planair- , . — . , .
: , , , -, , , , . , . , , , , , .
Il existe de nombreuses façons de créer des labyrinthes parfaits, et chacun d'eux a ses propres caractéristiques. Voici une liste d'algorithmes spécifiques. Tous décrivent la création d'un labyrinthe en découpant des passages, cependant, sauf indication contraire, chacun peut également être mis en œuvre en ajoutant des murs:
Backtracker récursif : - recursive backtracker, , . , , . , , . , . , . , , , . , . Recursive backtracking , , , .
: , . , «» , , . , , ( ). , . , , . , - , , . , , . , . , - (union-find algorithm): , . . , - .
Algorithme de Prim (vrai) : cet algorithme crée un arbre couvrant minimal en traitant des poids de bord aléatoires uniques. La quantité de mémoire requise est proportionnelle à la taille du labyrinthe. Nous partons de n'importe quel sommet (le labyrinthe fini sera le même, peu importe le sommet que nous commençons). Nous sélectionnons le bord du passage avec le plus petit poids reliant le labyrinthe à un point qui n'y est pas déjà, puis le fixons au labyrinthe. Le labyrinthe est terminé lorsque les bords en question ne sont plus laissés. Pour sélectionner efficacement le bord suivant, vous avez besoin d'une file d'attente prioritaire (généralement implémentée à l'aide d'un segment) qui stocke tous les bords de la bordure. Cependant, cet algorithme est plutôt lent car il faut du temps à log (n) pour sélectionner des éléments dans le tas. Par conséquent, il est préférable de préférer l'algorithme Kraskal, qui crée également un arbre couvrant minimal, car il est plus rapide et crée des labyrinthes avec une structure identique. En fait, avec la même graine aléatoire, les algorithmes Prima et Kraskal peuvent créer les mêmes labyrinthes.
Algorithme de Prim (simplifié) : cet algorithme de Prim crée un arbre couvrant minimal. Il est simplifié de telle sorte que tous les poids des bords sont les mêmes. Il nécessite une capacité mémoire proportionnelle à la taille du labyrinthe. Nous partons d'un pic aléatoire. Nous sélectionnons au hasard le bord du passage reliant le labyrinthe à un point qui n'y est pas encore, puis nous le fixons au labyrinthe. Le labyrinthe est terminé lorsque les bords en question ne sont plus laissés. Étant donné que les bords sont en apesanteur et non ordonnés, ils peuvent être stockés sous forme de liste simple, c'est-à-dire que la sélection des éléments de la liste sera très rapide et prend un temps constant. Par conséquent, il est beaucoup plus rapide que le véritable algorithme Prim avec des poids de bord aléatoires. La texture de labyrinthe créée aura un débit plus faible et une solution plus simple que la vraie méthode Prim, car elle se propage uniformément à partir du point de départ, comme le sirop renversé, et ne contourne pas les fragments de côtes avec un poids plus élevé, qui sont pris en compte plus tard.
Algorithme de Prim (modifié) : cet algorithme de Prim crée un arbre couvrant minimal, modifié de sorte que tous les poids des bords soient les mêmes. Cependant, il est implémenté de telle sorte qu'au lieu de bords, il regarde les cellules. La quantité de mémoire est proportionnelle à la taille du labyrinthe. Dans le processus de création, chaque cellule peut avoir l'un des trois types suivants: (1) «interne»: la cellule fait partie du labyrinthe et y est déjà découpée, (2) «limite»: la cellule ne fait pas partie du labyrinthe et n'y a pas encore été découpée, mais est située à côté de la cellule qui est déjà "interne", et (3) "externe": la cellule ne fait pas encore partie du labyrinthe, et aucun de ses voisins n'est également la cellule "interne". Nous commençons par choisir une cellule, la rendons «interne», et pour tous ses voisins, nous définissons le type sur «limite». Nous sélectionnons au hasard la cellule «limite» et y coupons un passage d'une des cellules «internes» voisines. Nous changeons l'état de cette cellule «limite» en «interne» et changeons le type de tous ses voisins de «externe» en «frontière». Le labyrinthe est achevé lorsqu'il ne reste plus de cellules «limites» (c'est-à-dire qu'il n'y a plus de cellules «externes», ce qui signifie que tout le monde est devenu «interne»). Cet algorithme crée des labyrinthes avec un indice de rendement très faible, a de nombreux blocages courts et une solution plutôt simple. Le labyrinthe résultant est très similaire au résultat de la méthode simplifiée de Prim, avec une légère différence: les vides dans l'arbre couvrant ne sont remplis que si une cellule limite est sélectionnée au hasard, contrairement à la triple probabilité de remplir cette cellule par l'une des cellules limites qui y mènent. De plus, l'algorithme est très rapide, plus rapide que l'algorithme Prim simplifié, car il n'a pas besoin de compiler et de traiter la liste des arêtes.
Algorithme d' Aldous-Broder : ce qui est intéressant dans cet algorithme, c'est qu'il est homogène, c'est-à-dire qu'il crée avec une probabilité égale tous les labyrinthes possibles d'une taille donnée. De plus, il ne nécessite ni mémoire supplémentaire ni pile. Nous sélectionnons un point et nous nous déplaçons au hasard vers une cellule voisine. Si nous entrons dans une cellule non coupée, découpez ensuite le passage de la cellule précédente. Nous continuons à nous déplacer vers les cellules voisines jusqu'à ce que nous coupions les passages à toutes les cellules. Cet algorithme crée des labyrinthes avec un faible débit, seulement légèrement supérieur à l'algorithme de Kraskal. (Cela signifie que pour un échange donné, il y a plus de labyrinthes avec un indice de rendement faible qu'avec des indices élevés, car le labyrinthe avec une probabilité moyenne est également faible.) La mauvaise chose à propos de cet algorithme est qu'il est très lent car il n'effectue pas de recherche intellectuelle pour ce dernier cellules, c'est-à-dire, en fait, n'a pas de garanties d'achèvement. Cependant, en raison de sa simplicité, il peut rapidement parcourir de nombreuses cellules, il se termine donc plus rapidement que vous ne le pensez. En moyenne, cela prend sept fois plus de temps que les algorithmes standard, bien que dans les mauvais cas, cela puisse être beaucoup plus long si le générateur de nombres aléatoires évite constamment les dernières cellules. Il peut être implémenté comme l'ajout de murs, si le mur de bordure est considéré comme un seul sommet, c'est-à-dire, par exemple, si le mouvement nous déplace vers le mur de frontière, nous nous téléportons à un point aléatoire le long de la frontière, et ensuite nous continuons à bouger. Dans le cas de l'ajout de murs, cela fonctionne presque deux fois plus vite, car la téléportation le long du mur frontalier permet un accès plus rapide aux parties éloignées du labyrinthe.
Algorithme de Wilson : il s'agit d'une version améliorée de l'algorithme Aldous-Broder, il crée des labyrinthes avec exactement la même texture (les algorithmes sont homogènes, c'est-à-dire que tous les labyrinthes possibles sont générés avec une probabilité égale), mais l'algorithme Wilson est beaucoup plus rapide. Il prend de la mémoire jusqu'à la taille du labyrinthe. Nous commençons avec une cellule de labyrinthe initiale choisie au hasard. Nous sélectionnons une cellule aléatoire qui ne fait pas encore partie du labyrinthe et effectuons une marche aléatoire jusqu'à ce que nous trouvions une cellule qui appartient déjà au labyrinthe. Dès que nous tombons sur la partie déjà créée du labyrinthe, nous retournons à la cellule aléatoire sélectionnée et coupons tout le chemin effectué en ajoutant ces cellules au labyrinthe. Plus précisément, lorsque nous revenons le long du chemin, nous coupons dans chaque cellule dans la direction dans laquelle la marche aléatoire a eu lieu la dernière fois que nous avons quitté la cellule. Cela évite l'apparition de boucles le long du chemin de retour, de sorte qu'un long passage rejoint le labyrinthe. Le labyrinthe est terminé lorsque toutes les cellules y sont attachées. L'algorithme a les mêmes problèmes de vitesse que Aldous-Broder, car il peut prendre beaucoup de temps pour trouver le premier chemin aléatoire vers la cellule initiale, mais après avoir placé plusieurs chemins, le reste du labyrinthe est découpé assez rapidement. En moyenne, il fonctionne cinq fois plus vite qu'Aldous-Broder, et moins de deux fois plus lentement que les meilleurs algorithmes. Il convient de noter que dans le cas de l'ajout de murs, cela fonctionne deux fois plus vite, car tout le mur de bordure fait initialement partie du labyrinthe, de sorte que les premiers murs se rejoignent beaucoup plus rapidement.
Algorithme de chasse et de destruction : cet algorithme est pratique car il ne nécessite pas de mémoire supplémentaire ou une pile, et convient donc à la création d'énormes labyrinthes ou labyrinthes sur des ordinateurs faibles en raison de l'impossibilité de manquer de mémoire. Comme il n'a pas de règles à suivre en permanence, il est également plus facile de modifier et de créer des labyrinthes avec différentes textures en l'utilisant. Il est presque similaire à un backtracker récursif, mais il n'y a pas de cellule non créée près de la position actuelle. On passe en mode «chasse» et on scrute systématiquement le labyrinthe jusqu'à trouver une cellule non créée à côté de la cellule déjà coupée. À ce stade, nous recommençons à couper dans ce nouvel emplacement. Le labyrinthe est terminé quand en mode «chasse» toutes les cellules sont scannées. Cet algorithme a tendance à créer des labyrinthes avec un débit élevé, mais pas aussi élevé que le backtracker récursif. Vous pouvez le forcer à générer des labyrinthes avec un débit plus faible, en entrant plus souvent en mode "chasse". Il s'exécute plus lentement en raison du temps passé à rechercher les dernières cellules, mais pas beaucoup plus lentement que l'algorithme de Kraskal. Il peut être implémenté selon le principe de l'ajout de murs, si vous vous téléportez occasionnellement au hasard pour éviter les problèmes inhérents à un backtracker récursif.
Algorithme croissant
arbre (algorithme d'arbre en croissance) : il s'agit d'un algorithme généralisé qui peut créer des labyrinthes avec différentes textures. La mémoire requise peut atteindre la taille du labyrinthe. Chaque fois qu'une cellule est coupée, nous l'ajoutons à la liste. Sélectionnez une cellule dans la liste et découpez le passage vers la cellule non créée à côté d'elle. S'il n'y a pas de cellules non créées à proximité de la cellule actuelle, supprimez la cellule actuelle de la liste. Le labyrinthe est terminé lorsqu'il n'y a rien d'autre dans la liste. La chose intéressante à propos de l'algorithme est que, selon la façon dont vous sélectionnez une cellule dans la liste, vous pouvez créer de nombreuses textures différentes. Par exemple, si vous sélectionnez toujours la dernière cellule ajoutée, cet algorithme se transforme en backtracker récursif. Si vous sélectionnez toujours des cellules au hasard, il se comporte de la même manière, mais pas de manière identique à l'algorithme Prim. Si vous sélectionnez toujours les cellules les plus anciennes ajoutées à la liste, nous créerons un labyrinthe avec l'indice de rendement le plus bas possible, même inférieur à celui de l'algorithme Prim. Si vous choisissez généralement la toute dernière cellule, mais que vous choisissez parfois une cellule aléatoire, le labyrinthe aura un débit élevé, mais une solution courte et directe. Si l'une des cellules les plus récentes est sélectionnée au hasard, le labyrinthe aura un faible débit, mais une solution longue et sinueuse.
Algorithme de forêt en croissance : il s'agit d'un algorithme plus généralisé combinant des types basés sur des arbres et des ensembles. Il s'agit d'une extension de l'algorithme de croissance arborescente, qui comprend essentiellement plusieurs instances se développant simultanément. Nous commençons avec toutes les cellules triées aléatoirement dans une liste de "nouvelles"; en outre, chaque cellule a son propre ensemble, comme au début de l'algorithme Kruskal. Sélectionnez d'abord une ou plusieurs cellules en les déplaçant de la liste des «nouvelles» vers la liste des «actives». Sélectionnez une cellule dans la liste "active" et découpez le passage à la cellule non créée suivante dans la liste "nouvelle", en ajoutant une nouvelle cellule à la liste des "actifs" et en combinant les ensembles de deux cellules. Si une tentative est faite pour couper dans la partie existante du labyrinthe, activez-la si les cellules sont dans des ensembles différents et combinez les cellules, comme cela se fait dans l'algorithme de Kraskal. S'il n'y a pas de «nouvelles» cellules près de la cellule actuelle, déplacez la cellule actuelle vers la liste des cellules «terminées». Le labyrinthe est terminé lorsque la liste des "actifs" devient vide. À la fin, nous combinons tous les ensembles restants, comme dans l'algorithme de Kruskal. Périodiquement, vous pouvez créer de nouveaux arbres en déplaçant une ou plusieurs cellules de la liste des "nouveaux" vers la liste des "actifs", comme cela a été fait au début. En contrôlant le nombre d'arbres d'origine et les parts des arbres nouvellement créés, vous pouvez générer de nombreuses textures uniques qui se combinent avec les paramètres déjà flexibles de l'algorithme de croissance des arbres.
Algorithme d'Eller : il s'agit d'un algorithme spécial, car il est non seulement plus rapide que tout le monde, mais n'a pas non plus de biais ou de lacunes évidents; en outre, lors de sa création, la mémoire est utilisée plus efficacement. Il ne nécessite même pas que tout le labyrinthe soit en mémoire, il utilise un volume proportionnel à la taille de la ligne. Il crée un labyrinthe ligne par ligne, une fois la génération de la chaîne terminée, l'algorithme n'en tient plus compte. Chaque cellule d'une rangée est contenue dans un ensemble; deux cellules appartiennent au même ensemble s'il y a un chemin entre elles le long du labyrinthe déjà créé. Ces informations vous permettent de découper des passages dans la ligne actuelle sans créer de boucles ou de zones isolées. En fait, il est assez similaire à l'algorithme de Kraskal, seulement ici il est formé une ligne à la fois, tandis que Kraskal regarde à travers tout le labyrinthe. La création d'une ligne se compose de deux parties: connectez de manière aléatoire les cellules adjacentes de la ligne, c'est-à-dire nous coupons les passages horizontaux, puis connectons au hasard les cellules entre la ligne actuelle et la ligne suivante, c'est-à-dire découpez les passages verticaux. Lors de la découpe de passages horizontaux, nous ne connectons pas les cellules qui sont déjà dans le même ensemble (car une boucle sera créée autrement), et lors de la découpe de passages verticaux, nous devons connecter une cellule si elle a une taille d'unité (car si vous la laissez, cela créera une zone isolée). Lors de la découpe de passages horizontaux, nous connectons les cellules si elles sont dans le même ensemble (car maintenant il y a un chemin entre elles), et lors de la découpe des passages verticaux lorsque nous ne nous connectons pas avec la cellule, nous le mettons dans un ensemble séparé (car maintenant il est séparé du reste du labyrinthe) ) La création commence par le fait qu'avant de connecter les cellules de la première ligne, chaque cellule a son propre ensemble. La création est terminée une fois les cellules connectées dans la dernière ligne. Il existe une règle spéciale d'achèvement: au moment de l'achèvement, chaque cellule doit être dans le même ensemble afin d'éviter les zones isolées. (La dernière ligne est créée en combinant chacune des paires de cellules voisines qui ne sont pas encore dans le même ensemble.) Il est préférable d'implémenter l'ensemble en utilisant une liste cyclique de cellules doublement liées (qui peut être juste un tableau qui lie des cellules à des paires de cellules des deux côtés du même ensemble), permettant effectuer l'insertion, la suppression et la vérification de la présence de cellules voisines dans un ensemble pendant un temps constant. Le problème avec cet algorithme est le déséquilibre dans le traitement des différents bords du labyrinthe; Pour éviter les taches dans les textures, vous devez connecter et ignorer les cellules de connexion dans les bonnes proportions.
Division récursive: cet algorithme est quelque peu similaire au backtracking récursif, car ils utilisent tous deux des piles, seulement il ne fonctionne pas avec les allées, mais avec les murs. Nous commençons par créer un mur horizontal ou vertical aléatoire qui intersecte une zone accessible dans une ligne ou une colonne aléatoire, et placons au hasard des espaces vides le long de celle-ci. Ensuite, nous répétons récursivement le processus pour les deux sous-régions générées par le mur de séparation. Pour de meilleurs résultats, vous devez ajouter une déviation dans le choix de l'horizontale ou de la verticale en fonction des proportions de la zone, par exemple, une zone dont la largeur est le double de la hauteur doit être plus souvent divisée par des murs verticaux. C'est l'algorithme le plus rapide sans déviation de direction, et souvent il peut même rivaliser avec des labyrinthes basés sur des arbres binaires, car il crée plusieurs cellules en même temps, bien qu'il présente un inconvénient évident sous la forme de longues parois coupant l'intérieur du labyrinthe. Cet algorithme est une sorte de labyrinthe fractal intégré, mais au lieu de créer constamment des labyrinthes de cellules de taille fixe avec des labyrinthes de même taille à l'intérieur de chaque cellule, il divise au hasard une zone donnée en un labyrinthe de taille aléatoire: 1x2 ou 2x1. La division récursive ne peut pas être utilisée pour découper des passages, car cela conduit à la création d'une solution évidente qui suit le long du bord extérieur ou intersecte directement l'intérieur.
Labyrinthes basés sur des arbres binaires : en fait, ce sont les algorithmes les plus simples et les plus rapides possibles, cependant, les labyrinthes créés ont une texture avec un biais très élevé. Pour chaque cellule, nous coupons un passage vers le haut ou vers la gauche, mais jamais dans les deux sens. Dans la version avec ajout de murs, un segment de mur est ajouté pour chaque sommet menant vers le bas ou vers la droite, mais pas dans les deux directions. Chaque cellule est indépendante de toutes les autres cellules, car nous n'avons pas besoin de vérifier l'état de certaines autres cellules lors de sa création. Il s'agit donc d'un véritable algorithme de génération de labyrinthes sans mémoire, non limité par la taille des labyrinthes créés. En fait, il s'agit d'un arbre binaire, si nous considérons le coin supérieur gauche comme une racine, et chaque nœud ou cellule a un nœud parent unique, qui est une cellule au-dessus ou à gauche de celui-ci. Les labyrinthes basés sur des arbres binaires sont différents des labyrinthes idéaux standard, car plus de la moitié des types de cellules ne peuvent pas exister en eux. Par exemple, il n'y aura jamais d'intersections et toutes les impasses ont des passages menant vers le haut ou vers la gauche, et ne menant jamais vers le bas ou vers la droite. Les labyrinthes ont tendance à avoir des passages menant en diagonale du coin supérieur gauche au coin inférieur droit, et il est beaucoup plus facile de se déplacer du coin inférieur droit au coin supérieur gauche. Vous pouvez toujours vous déplacer vers le haut ou vers la gauche, mais jamais simultanément dans les deux sens, vous pouvez donc toujours vous déplacer de manière déterministe en diagonale vers le haut et vers la gauche, sans rencontrer d'obstacles. Vous aurez la possibilité de choisir et de tomber dans des impasses en vous déplaçant vers le bas et vers la droite. , , , .
Sidewinder: , . : , , . , , , , , . , ( , ). , sidewinder . , sidewinder . , sidewinder , , . sidewinder , « ». , sidewinder — , , , , . sidewinder , , , .
| Algorithme | % impasses | Tapez | Priorité | Pas de parti pris? | Homogène? | La mémoire | Le temps | % solution |
| Itinéraire unique | 0 | Arbre | Les murs | Oui | Jamais | N ^ 2 | 379 | 100,0 |
| Backtracker récursif | 10 | Arbre | Passerelles | Oui | Jamais | N ^ 2 | 27 | 19,0 |
| Chasser et tuer | 11 (21) | Arbre | Passerelles | Oui | Jamais | 0 | 100 (143) | 9,5 (3,9) |
| Division récursive | 23 | Arbre | Les murs | Oui | Jamais | N * | 10 | 7.2 |
| Arbre binaire | 25 | Beaucoup | Les deux | Non | Jamais | 0 * | 10 | 2.0 |
| Sidewinder | 27 | Beaucoup | Les deux | Non | Jamais | 0 * | 12 | 2.6 |
| Algorithme Eller | 28 | Beaucoup | Les deux | Non | Non | N * | 20 | 4,2 (3,2) |
| Algorithme de Wilson | 29 | Arbre | Les deux | Oui | Oui | N ^ 2 | 48 (25) | 4.5 |
| Algorithme Aldous-Broder | 29 | Arbre | Les deux | Oui | Oui | 0 | 279 (208) | 4.5 |
| Algorithme de Kraskal | 30 | Beaucoup | Les deux | Oui | Non | N ^ 2 | 33 | 4.1 |
| Algorithme Prima (vrai) | 30 | Arbre | Les deux | Oui | Non | N ^ 2 | 160 | 4.1 |
| Algorithme Prima (simplifié) | 32 | Arbre | Les deux | Oui | Non | N ^ 2 | 59 | 2.3 |
| Algorithme Prima (modifié) | 36 (31) | Arbre | Les deux | Oui | Non | N ^ 2 | 30 | 2.3 |
| La croissance des arbres | 49 (39) | Arbre | Les deux | Oui | Non | N ^ 2 | 48 | 11,0 |
| Croissance des forêts | 49 (39) | Les deux | Les deux | Oui | Non | N ^ 2 | 76 | 11,0 |
Ce tableau résume les caractéristiques des algorithmes de création de labyrinthes idéaux décrits ci-dessus. À titre de comparaison, un algorithme de labyrinthe à itinéraire unique a été ajouté (théoriquement, les labyrinthes à itinéraire unique sont idéaux). Explication de la colonne:- : , , , 2D-. . , , , . 10% ( ) 49% ( ). Recursive Backtracker 1%. 66%: .
- : : , , . , , , , . , , .
- : , . . , , . Recursive Backtracker , , , . , , . , Hunt and Kill , , .
- : , . , . Sidewinder , . , . Hunt and Kill , , , .
- : . «» , . «» , , . «» , , . , .
- : , . , , (N), (N^2). , ( ). , , . Sidewinder , . , .
- : , , , . , ( 10), . 100x100 Daedalus. , , , .
- : , , . , 100x100 . . «» . , . , . , , , .
Il existe de nombreuses façons de résoudre des labyrinthes, et chacun d'eux a ses propres caractéristiques. Voici une liste d'algorithmes spécifiques:
Suivre le long des murs (suiveur de mur) : . («»), . ( ). , ( ) . , . , , . , , , . 3D- , 3D- 2D-, .. , -, -, .
: , «» , . 2D- , , .. . , , . . , , . , , . , , . , , — -1, — 1. , , .. 360 , «». , «», , , , , . , , . , — , .
: (Chain algorithm) , ( ) . , , . , . , , . , . ( ) , . . , , . «» , . , , , . , . , .
Recursive backtracker: , . , . : ( ), «», , , «», , . , , «»; «» . (backtracking) , , . , . , , .
(Trémaux's algorithm): . recursive backtracker : , . , . , , . , , , . ( , .) , (.. ), , , , (.. , ). , , , , , . , . , , .
(Dead end filler) : . , . , , . , . , , . , , .
Cul-de-sac filler : , , . dead end filler, , . ( — , , ) , . dead end filler. , , , , . , , , dead end filler.
Blind alley filler : , , . , . — , , . , , cul-de-sac filler, . . , , , , . , , , ( ). , , . , cul-de-sac filler - , collision solver , - .
Blind alley sealer : blind alley filler , , . . . , , blind alley filler, . . , , , , . , , . , . , , . , , .
(Shortest path finder): , , . , , . collision solver, , , «» , ( ), «» , , . «», , . , - , . , , , A* , .
(Shortest paths finder) : , . , , , , , , , - , . , , , «» , , , . , , , , . , .- Collision solver: "amoeba" solver. . , . «» , ( ). « » ( ), , . «», , , , . ( , «», . , , , .) , shortest paths finder, ( ) ( ).
- Random mouse: , , .. , . 180 , . , , . , , .
| | ? | | ? | ? | ? | ? |
| Random Mouse | 1 | Non | Tu es | / | Non | | Non |
| Wall Follower | 1 | Non | Tu es | / | | | |
| 1 | Non | Tu es | / | | | |
| 1 | | + | Non | | Non | |
| Backtracker récursif | 1 | Oui | Tu es | Non | Oui | Non | Oui |
| Algorithme Tremo | 1 | Oui | Tu es | À l'intérieur / sur | Non | Non | Oui |
| Remplisseur de cul-de-sac | Tous + | Non | Labyrinthe | Plus | Non | Oui | Oui |
| Remplisseuse cul-de-sac | Tous + | Non | Labyrinthe | Plus | Non | Oui | Oui |
| Scellant pour allées aveugles | Tous + | Oui | Labyrinthe | Non | Non | Non | Oui |
| Remplisseur de ruelle aveugle | Tous | Oui | Labyrinthe | Plus | Non | Oui | Non |
| Solveur de collision | Tout court | Oui | Vous + | Non | Non | Non | Oui |
| Rechercher les chemins les plus courts | Tout court | Oui | Vous + | Non | Oui | Non | Oui |
| Rechercher le chemin le plus court | 1 plus court | Oui | Vous + | Non | Oui | Non | Oui |
Ce tableau répertorie brièvement les caractéristiques des algorithmes de résolution de labyrinthe décrits ci-dessus. Selon ces critères, il est possible de classer et d'évaluer des algorithmes de résolution de labyrinthes. Explications des colonnes:
- Solutions: décrit les solutions trouvées par l'algorithme et les actions de l'algorithme, s'il y en a plusieurs. L'algorithme peut choisir une solution ou en laisser plusieurs. De plus, la ou les solutions peuvent être n'importe quel chemin ou le chemin le plus court. Le remplissage en cul-de-sac et le cul-de-sac (ainsi que le scellant pour allée aveugle lors du traitement de ses zones inaccessibles) laissent toutes les solutions, mais ils peuvent également laisser des passages qui ne se trouvent dans aucun des chemins de solution, je les ai donc marqués comme «Tous + ".
- Garantie: L'algorithme est-il garanti pour trouver au moins une solution? Pour la souris aléatoire, «non» est indiqué, car son achèvement n'est pas garanti, et pour le suiveur de mur et l'algorithme du Collège, «non» est indiqué, car ils ne pourront pas trouver de solution si la cible est à l'intérieur de l'île. «Dead» est indiqué pour les enduits sans issue et les enduits en cul-de-sac, car dans les labyrinthes en osier, ils peuvent ne pas trouver de solution.
- Priorité: Il existe deux types d'algorithmes pour résoudre le labyrinthe: donner la priorité à «vous» (situé dans le labyrinthe) ou donner la priorité au labyrinthe. Si la priorité vous est donnée, alors nous avons un point («Vous» est indiqué dans le tableau) ou plusieurs points («Vous +») et l'algorithme essaie de les dessiner du début à la fin du labyrinthe. Si la priorité est donnée au labyrinthe, alors nous examinons le labyrinthe dans son ensemble et éliminons les passages inutiles.
- Disponible pour l'homme: un homme peut-il utiliser l'algorithme pour résoudre le labyrinthe, soit dans le vrai labyrinthe, soit en regardant la carte d'en haut. Certains des algorithmes qui donnent la priorité à «vous» peuvent être implémentés en tant que personne à l'intérieur du labyrinthe (ou au-dessus), et certains qui donnent la priorité au labyrinthe peuvent être implémentés en tant que personne, mais uniquement au-dessus du labyrinthe. D'autres algorithmes sont trop complexes et leur implémentation fiable n'est possible que sur ordinateur.
- Pass indépendant: l'algorithme peut-il s'exécuter n'importe où. Certains algorithmes exigent que le labyrinthe ait des passages évidents ou, en parlant dans la terminologie des graphiques, des bords nets entre les sommets individuels, ou des passages d'un pixel lorsqu'il est implémenté sur un ordinateur. Le suiveur de mur, l'algorithme Pledge et l'algorithme de circuit nécessitent un mur uniquement sur un côté de vous. Le backtracker récursif et le plus court localisateur de chemin acheminent le leur à travers des espaces ouverts.
- Aucune mémoire requise: avez-vous besoin de mémoire supplémentaire ou d'une pile pour implémenter l'algorithme. Les algorithmes efficaces ne nécessitent qu'une image bitmap du labyrinthe lui-même et ils n'ont pas besoin d'ajouter de marqueurs au labyrinthe dans le processus de résolution.
- Rapide: le processus de décision est-il considéré comme rapide? Les algorithmes les plus efficaces suffisent à ne regarder chaque cellule du labyrinthe qu'une seule fois, ou ils peuvent en ignorer complètement certaines parties. Le temps d'exécution doit être proportionnel à la taille du labyrinthe, ou O (n ^ 2), où n est le nombre de cellules le long d'un côté. La souris aléatoire est lente car son achèvement n'est pas garanti, et le remplissage en allée aveugle résout potentiellement le labyrinthe de chaque fourche.
Autres opérations avec des labyrinthes
En plus de créer et de résoudre des labyrinthes, vous pouvez effectuer d'autres opérations avec eux:

Fill: c'est une fonction «rapide et sale», mais néanmoins utile qui peut être implémentée en un seul appel à la procédure de bibliothèque graphique Fill ou FloodFill. Nous effectuons le FloodFill du passage au début, et si la fin n'est pas inondée, alors le labyrinthe n'a pas de solution. Dans les labyrinthes, dont l'entrée et la sortie sont sur les bords, nous effectuons le FloodFill d'un mur, et les bords restants marquent la solution. Dans les labyrinthes où le début et la fin sont à l'intérieur, nous exécutons le FloodFill du mur d'enceinte, et si le mur de sortie n'a pas été supprimé, ce labyrinthe ne peut pas être résolu en suivant le long des murs. De nombreuses méthodes de création de labyrinthes et d'autres fonctions utilisent le "remplissage" du labyrinthe à certains points.
Dissolvant d'isolement: changez le labyrinthe afin qu'il ne comporte pas de parties avec des passages inaccessibles depuis le reste du labyrinthe. Il est réalisé en enlevant les murs reliant ces parties avec le reste du labyrinthe. Nous commençons par une copie du labyrinthe, puis remplissons le passage vers le début. Nous scannons le labyrinthe (de préférence dans un ordre aléatoire, mais avec une visite à toutes les cellules possibles) pour la présence de cellules non remplies adjacentes à la cellule remplie. Nous supprimons le segment de mur à ce point dans le labyrinthe d'origine, remplissons le labyrinthe à ce nouveau point et répétons jusqu'à ce que toutes les pièces soient remplies. Cette fonction est utilisée pour créer des labyrinthes tissés et à motifs.
Suppression des boucles: modifiez le labyrinthe afin qu'il n'y ait pas de boucles et de murs qui ne soient connectés à rien, et que chaque partie du labyrinthe soit accessible à partir de n'importe quel point d'une seule manière. La mise en œuvre de cette fonction est presque similaire à la suppression des zones isolées, seulement nous percevons les murs comme des passages, et vice versa. Nous commençons par une copie du labyrinthe, puis remplissons les murs extérieurs. Nous scannons le labyrinthe (de préférence dans un ordre aléatoire, mais avec une visite à tous les sommets de murs possibles) pour la présence de murs non remplis à côté de ceux remplis. Ajoutez un segment de mur reliant les deux parties des murs au labyrinthe d'origine à ce stade, remplissez le labyrinthe à ce nouveau point et répétez jusqu'à ce que toutes les parties soient remplies. Cette fonction est utilisée pour créer des labyrinthes modèles et peut être utilisée pour convertir des labyrinthes en osier à des labyrinthes idéaux, qui restent néanmoins similaires aux originaux.
Rechercher les goulots d'étranglement : Rechercher dans le dédale de passages ou de points d'intersection par lesquels passent toutes les solutions de ce dédale. Pour ce faire, commencez à suivre le long des murs avec la méthode de la main gauche pour obtenir la solution de gauche et commencez à suivre le long des murs avec la méthode de la main droite pour obtenir la bonne solution. Les endroits où les deux solutions sont communes sont des goulots d'étranglement. Cependant, cette technique ne fonctionne que pour les labyrinthes, qui peuvent être résolus avec succès en suivant le long des murs. Dans d'autres labyrinthes, pour trouver des goulots d'étranglement, vous devez trouver n'importe quelle solution, ainsi que exécuter un scellant pour allée aveugle (cela peut rendre le labyrinthe insoluble s'il perçoit l'entrée ou la sortie à l'intérieur du labyrinthe comme une grande impasse). Des parties du chemin de solution passant par des passages fermés sont des goulots d'étranglement.
Implémentations d'algorithmes
- Daedalus : tous les algorithmes de création et de résolution de labyrinthes décrits ci-dessus sont implémentés dans Daedalus, un programme Windows gratuit et téléchargeable. Complet avec Daedalus il y a un code source complet.