Il est plus difficile d'écrire sur les mathématiques (pour que ce soit intéressant) que sur la physique. Cependant, j'espère que vous lirez au moins les exemples de programmes C fous.
Les monstres peuvent se développer à partir de choses complètement inoffensives. Prenons, par exemple, le jeu des sous-chaînes. Nous écrivons une chaîne de lettres a et b et sélectionnons les sous-chaînes du caractère 1 au caractère 2, de 2 à 4, de trois à 6, de n à 2n, jusqu'à ce que la longueur de la chaîne principale soit suffisante. Notre tâche est de nous assurer que dans ces sous-chaînes le plus court n'entre plus. J'ai même écrit un analyseur SQL:
declare @s varchar(max) = 'abbbaaaaaaab' declare @n int=1 declare @sub table (n int, sub varchar(max)) while @n*2<=len(@s) begin insert into @sub select @n,substring(@s,@n,@n+1) set @n=@n+1 end select *,(select max(sub) from @sub I where In>On and charindex(O.sub,I.sub)>0) as FoundMatch from @sub O order by 1
Voici un exemple de sortie:
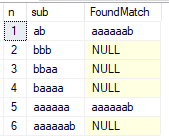
Comme vous pouvez le voir, les sous-chaînes 1 et 5 n'ont pas réussi le test. Nous pouvons supprimer le dernier caractère et la chaîne de 11 caractères résultante «abbbaaaaaaaa» réussira le test. Il s'avère que c'est la chaîne la plus longue possible dans l'alphabet à deux caractères qui remplit cette condition.
Pour un alphabet d'un caractère, la longueur de chaîne maximale est de 3, puis pour des raisons purement techniques. Il s'avère que la longueur maximale est finie pour un alphabet de n'importe quel nombre de lettres. Nous avons donc:
f ( 1 ) = 3
f ( 2 ) = 11
f ( 3 ) = ? ? ?
Testez votre intuition sur la durée d'une chaîne dans un alphabet à trois lettres. 100? 1000? En fait, bien plus que Googol, et bien plus que GoogolPlekh.
f ( 3 ) > 2 u p a r r o w 7198 158836
Et je dois passer du temps à montrer la force des tireurs.
Flèches (hyperopération)
Nous utilisons la multiplication pour ne pas écrire de nombreuses opérations d'addition:

Nous utilisons l'exponentiation afin de ne pas écrire de nombreuses multiplications:

En considérant l'addition comme une opération de niveau 0, la multiplication comme 1, l'exponentiation comme 2, nous pouvons introduire l'opération «flèche», par exemple,

Notez que les parenthèses sont déjà importantes ici. Le niveau suivant est l'opération à deux flèches:
3 uparrow uparrow3=3 uparrow(3 uparrow3)=3 uparrow7625597484987=33...3
La dernière pyramide de triples a une hauteur de 7 milliards, et ce nombre est déjà beaucoup, beaucoup plus grand que googol et googolpleks. Nous désignons ce nombre énorme comme
Darkness (c'était un tel chiffre dans l'ancienne langue russe) et essayons de faire un pas de plus:
3 uparrow33=3 uparrow uparrow uparrow3=3 uparrow uparrow(3 uparrow uparrow3)=3 uparrow uparrowobscurité=3 uparrow3 uparrow3... uparrow3
(et tant de fois) ... On imagine même déjà à quel point ce nombre est important. Veuillez noter que lorsqu'il y a beaucoup de flèches, nous écrivons un répéteur en haut. Vous pouvez donc comprendre à quel point
f(3)>2 uparrow7198158836
Et bien plus
À l'aide de flèches, seul le plus petit des grands nombres est créé, pour ainsi dire. Le taux de croissance des fonctions est mesuré à une certaine échelle - en le comparant à
des fonctions à croissance rapide . La première fonction de cette hiérarchie correspond à l'addition, la seconde à la multiplication, la troisième à la flèche et les n-èmes à n-2 flèches (approximativement, pas exactement). Mais vous pouvez définir
fw(n)=fn(n)
Une telle fonction pour n = 3 est comparable à une flèche, pour n = 4 à deux flèches, et à mesure que le paramètre n croît, elle dépasse la croissance de la fonction avec n'importe quel nombre statique de flèches.
Vous pouvez aller encore plus loin:
fw,fw+1,fw+n,fw2,fw2,fww,fwww,f epsilon Ces fonctions sont indexées par des ordinaux, ou dans la littérature russe par des nombres ordinaux. L'image avec la structure des nombres ordinaux initiaux précède l'article, mais ils s'étendent beaucoup plus loin et commencent plus loin
Petit mysticisme
La pyramide sans fin des oméga donne un ordinal
e p s i l o n 0 . Lisez à propos de la
fonction dont la croissance est mesurée par cet ordinal. Il s'avère qu'une fonction croît si vite que l'arithmétique formelle ne peut en principe prouver qu'une telle fonction est définie du tout!
Bien sûr, vous savez sur le théorème de Godel qu'il y a des déclarations non prouvables. Mais, en règle générale, le seul exemple d’une telle déclaration est la construction même de Gödel («Je ne suis pas démontrable»). Le théorème de Goodstein est un bon exemple d'une telle affirmation.
De plus, il s'avère que les ordinaux
mesurent en quelque sorte
la puissance des théories . La «force» de l'arithmétique formelle est
e p s i l o n 0 , la
théorie simplifiée des ensembles de Kripke-Plateka a la force de l'
ordinal de Feferman-Schutte , etc.
Tin - Maths tourniquet - Concours de langue C
Un concours a été organisé pour générer un grand nombre. Non, la programmation d'une machine de Turing est encore trop cruelle, donc C a été utilisé pour une machine infinie abstraite avec sizeof (int) = infinity. Vous pouvez également utiliser malloc () et la quantité de mémoire, comme la pile, est illimitée. Seule la longueur du programme était limitée - le programme devait tenir sur 512 octets (hors espaces), mais l'utilisation d'un préprocesseur (#define) était autorisée.
Les résultats sont publiés sur
le site Web de mathématiques . Découvrez en même temps le design du site d'un vrai mathématicien. Les résultats sont
ici . Voici le texte du programme, qui a pris la deuxième place, donnant le nombre de
f w w ( 10 500 )
typedef int J; JP(J x,J y) { return x+y ? x%2 + y%2*2 + P(x/2,y/2)*4 : 0 ;} JH(J z) { return z ? z%2 + 2*H(z/4) : 0 ;} JI(J f,J e,J r){ return f ? P(P(f,e),r) : r ;} JM(J x,J e) { return x ? I(x%2, M(e,0), M(x/2, e+1)) : 0 ;} JD(J,J); JE(J f,J e,J r,J b) { return e ? E(1, D(e,b), I(b-1, D(e,b), I(f-1,e,r)), b) : I(f-1,e,r) ; } JD(J x,J b) { return x ? E( H(H(x)), H(H(x)/2), H(x/2), b) : 0 ;} JF(J x,J b) { return x ? F(D(x,b+1),b+1) : b ;} JG(J x) { return F(M(x,9), 9) ;} J f(J n,J x) { return n ? f(n-1, G(x ? f(n,x-1) : n)) : G(x) ;} J g(J x) { return f(x,x) ;} J h(J n,J x) { return n ? h(n-1, g(x ? h(n,x-1) : n)) : g(x) ;} J main(void) { return h(g(9),9) ;}
Le texte du programme du gagnant est plus long, je voulais juste montrer où il commence:
#define R { return #define PP ( #define LL ( #define TS (v, y, c, #define C ), #define X x) #define F );}
Mais même l'organisateur du concours a eu du mal à évaluer la taille du nombre (écrit
très gros )
Castors occupés
D'accord, assez pour faire face à de petits nombres, faisons-en de grands. Imaginez qu'un concours universel ait été organisé pour écrire un programme pour générer le plus grand nombre. Comme le nombre de programmes ne dépasse pas 512 caractères, il y a bien sûr toujours un gagnant absolu. Désignons-le comme BB (512) -
fonction de castor occupé .
Il est clair que BB (1024) >> BB (512). Mais à quelle vitesse la fonction BB se développe-t-elle? Il s'avère que sa croissance est plus rapide que tout ce que nous avons rencontré. La fonction BB elle-même est insoluble sur le plan algorithmique; elle ne peut pas être calculée sur un ordinateur. Mais à mesure que la durée du programme valide augmente, nous pouvons mettre en œuvre de plus en plus de nouvelles idées. BB croît donc plus rapidement que toute fonction décidable par algorithme.
GRAND PIED
D'accord, assez pour faire face à de petits nombres, faisons-en de grands. Ah, je l'ai déjà dit? Ce serait cool d'exécuter BB (BB (n)). Mais comme BB n'est pas calculable, cela pose des problèmes techniques (une telle fonction est calculable dans les machines Turing avec des oracles - ne pas confondre les oracles avec Oracle DBMS).
Mais vous pouvez le faire plus facilement, au lieu d'un
programme, considérez une
formule avec des quantificateurs de longueur n. Une formule de quantification n'a pas d'importance si quelque chose est calculable ou non. Vous pouvez donc au moins prendre la fonction BB (1 000 000 000) et l'appliquer à vous-même BB (BB (BB (1 000 000))) fois. Et c'est seulement ce qui m'est venu à l'esprit.
Le plus grand nombre pouvant être indiqué par une formule d'au plus n caractères est indiqué par FOOT (n).
G R A N D P I E D = P I E D 10 ( 10 100 )
PS
Pour le prochain article, je voudrais comprendre sur quoi se concentrer, participez à l'enquête s'il vous plaît