🧑🏾‍🤝‍🧑🏽 ⚜️ 🍼 Diminution de la taille de l'échantillon des données expérimentales sans perte d'informations ✊ 🛢️ ⛹🏽

Quel est le problème des histogrammes de données expérimentales

La base de la gestion de la qualité des produits de toute entreprise industrielle est la collecte de données expérimentales avec leur traitement ultérieur.

Le traitement initial des résultats expérimentaux consiste à comparer les hypothèses sur la loi de distribution des données, qui décrit, avec la plus petite erreur, une variable aléatoire sur l'échantillon observé.

Pour cela, l'échantillon est présenté sous la forme d'un histogramme composé de

k

$k$ colonnes construites à intervalles de longueur

d

$d$ .

L'identification de la forme de la distribution des résultats de mesure nécessite également un certain nombre de problèmes dont l'efficacité de la solution diffère pour différentes distributions (par exemple, en utilisant la méthode des moindres carrés ou en calculant les estimations d'entropie).

De plus, l'identification de la distribution est également nécessaire car la dispersion de toutes les estimations (écart type, excès, kurtosis, etc.) dépend également de la forme de la loi de distribution.

Le succès de l'identification de la forme de distribution des données expérimentales dépend de la taille de l'échantillon et, si elle est petite, les caractéristiques de distribution sont masquées par le caractère aléatoire de l'échantillon lui-même. En pratique, il n'est pas possible de fournir un échantillon de grande taille, par exemple supérieur à 1 000, pour diverses raisons.

Dans une telle situation, il est important de répartir les données d'échantillonnage de la meilleure manière dans les intervalles, lorsque la série d'intervalles est nécessaire pour une analyse et des calculs supplémentaires.

Par conséquent, pour une identification réussie, il est nécessaire de résoudre le problème d'attribution du nombre d'intervalles k

A. Hald dans le livre [1] convainc largement qu'il existe un nombre optimal d'intervalles de regroupement lorsque l'enveloppe pas à pas de l'histogramme construit sur ces intervalles est la plus proche de la courbe de distribution lisse de la population générale.

L'un des signes pratiques de l'approche de l'optimum est la disparition des creux dans l'histogramme, puis le plus grand k est considéré comme proche de l'optimum, auquel l'histogramme conserve toujours un caractère lisse.

De toute évidence, le type d'histogramme dépend de la construction d'intervalles d'appartenance à une variable aléatoire, cependant, même dans le cas d'une partition uniforme, une méthode satisfaisante pour cette construction n'est toujours pas disponible.

La partition, qui pourrait être considérée comme correcte, conduit au fait que l'erreur d'approximation par la fonction constante par morceaux de la densité de distribution supposée continue (histogramme) sera minimale.

Les difficultés sont dues au fait que la densité estimée est inconnue; par conséquent, le nombre d'intervalles affecte fortement la forme de la distribution de fréquence de l'échantillon final.

Pour une longueur d'échantillon fixe, l'élargissement des intervalles de partition conduit non seulement à un raffinement de la probabilité empirique d'y entrer, mais aussi à une perte inévitable d'informations (à la fois au sens général et au sens de la courbe de distribution de densité de probabilité), donc, avec un agrandissement non justifié, la distribution étudiée est trop lissée .

Une fois qu'elle est apparue, la tâche de diviser de manière optimale la plage sous l'histogramme ne disparaît pas du champ de vision des spécialistes, et jusqu'à ce que le seul avis établi sur sa solution apparaisse, la tâche restera pertinente.

Choix des critères d'évaluation de la qualité de l'histogramme des données expérimentales

Le critère de Pearson, comme on le sait, nécessite de diviser l'échantillon en intervalles - c'est en eux que la différence entre le modèle adopté et l'échantillon comparé est évaluée.

c h i^{2} = s u m_{j = 1}^{m} f r a c (E_{j} - M_{j})^{2} M_{j}

$\ chi ^ {2} = \ sum_ {j = 1} ^ {m} \ frac {(E_ {j} -M_ {j}) ^ {2}} {M_ {j}}$

où:

E_{j}

$E_ {j}$ - fréquences expérimentales

(n_{j})

$(n_ {j})$ ;

M_{j}

$M_ {j}$ - valeurs de fréquence dans la même colonne; nombre m de colonnes d'histogramme.

Cependant, l'application de ce critère dans le cas d'intervalles de longueur constante, habituellement utilisés pour construire des histogrammes, est inefficace. Par conséquent, dans les travaux sur l'efficacité du critère de Pearson, les intervalles ne sont pas considérés avec une longueur égale, mais avec une probabilité égale conformément au modèle accepté.

Dans ce cas, cependant, le nombre d'intervalles de longueur égale et le nombre d'intervalles de probabilité égale diffèrent plusieurs fois (à l'exception d'une distribution également probable), ce qui permet de douter de la fiabilité des résultats obtenus dans [2].

Comme critère de proximité, il est conseillé d'utiliser le coefficient d'entropie, calculé comme suit [3]:

k_{e} = f r a c d n 2 s i g m a 10^{b e t a}

$k_ {e} = \ frac {dn} {2 \ sigma} 10 ^ {\ beta}$

b e t a = - f r a c 1 n s u m_{i = 1}^{m} n_{i} l g (n_{i})

$\ beta = - \ frac {1} {n} \ sum_ {i = 1} ^ {m} {n_ {i} lg (n_ {i})}$

où:

n_{i}

$n_ {i}$ - le nombre d'observations dans le i-ème intervalle

i = 0, . . ., m

$i = 0, ..., m$

Algorithme pour évaluer la qualité de l'histogramme des données expérimentales à l'aide du coefficient d'entropie et du module numpy.histogram

La syntaxe d'utilisation du module est la suivante [4]:

numpy.histogram (a, bins = m, range = None, normed = None, poids = None, densité = None)

Nous considérerons les méthodes pour trouver le nombre optimal m d' intervalles de fractionnement d'histogramme implémentés dans le module numpy.histogram:

• «auto» - notes maximales de «sturges» et «fd» , offre de bonnes performances;
• «fd» (Freedman Diaconis Estimator) - un évaluateur fiable (résistant aux émissions) qui prend en compte la variabilité et la taille des données;
• «doane» - une version améliorée de l'estimation des sturges qui fonctionne plus précisément avec des ensembles de données avec une distribution non normale;
• «scott» est un évaluateur moins fiable qui prend en compte la variabilité et la taille des données;
• «pierre» - l'évaluateur est basé sur un recoupement de l'estimation du carré de l'erreur, peut être considéré comme une généralisation de la règle de Scott;
• «riz» - l'évaluateur ne prend pas en compte la variabilité, mais uniquement la taille des données, surestime souvent le nombre d'intervalles requis;
• «sturges» - une méthode (par défaut) qui ne prend en compte que la taille des données, est optimale uniquement pour les données gaussiennes et sous-estime le nombre d'intervalles pour les grands ensembles de données non gaussiens;
• 'sqrt' est l'estimateur de racine carrée pour la taille des données utilisée par Excel et d'autres programmes pour des calculs rapides et faciles du nombre d'intervalles.

Pour commencer la description de l'algorithme, nous adaptons le module numpy.histogram () pour calculer le coefficient d'entropie et l'erreur d'entropie:

from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#       m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#  ke=h/std (a)#    (1). return ke,h

Considérons maintenant les principales étapes de l'algorithme:

1) Nous formons un échantillon témoin (ci-après dénommé "grand échantillon") qui répond aux exigences de l'erreur de traitement des données expérimentales . À partir d'un grand échantillon, en supprimant tous les membres impairs, nous formons un échantillon plus petit (ci-après dénommé le "petit échantillon");

2) Pour tous les évaluateurs 'auto', 'fd', 'doane', 'scott', 'stone', 'rice', 'sturges', 'sqrt' nous calculons le coefficient d'entropie ke1 et l'erreur h1 pour un grand échantillon et le coefficient d'entropie ke2 et l'erreur h2 pour un petit échantillon, ainsi que la valeur absolue de la différence - abs (ke1-ke2);

3) En contrôlant les valeurs numériques des évaluateurs au niveau d'au moins quatre intervalles, nous sélectionnons l'évaluateur qui fournit la valeur minimale de la différence absolue - abs (ke1-ke2).

4) Pour la décision finale sur le choix d'un évaluateur, nous construisons sur un histogramme les distributions pour les grands et les petits échantillons avec l'évaluateur fournissant la valeur abs minimale (ke1-ke2), et sur la seconde avec l'évaluateur fournissant la valeur abs maximale (ke1-ke2). L'apparition de sauts supplémentaires dans un petit échantillon dans le deuxième histogramme confirme le bon choix de l'évaluateur dans le premier.

Considérons le travail de l'algorithme proposé sur un échantillon de données d'une publication [2]. Les données ont été obtenues en sélectionnant au hasard 80 blancs sur 500 avec mesure ultérieure de leur masse. La pièce doit avoir une masse dans les limites suivantes:

m = 17_{- 0, 4}^{+ 0, 6}

$m = 17 _ {- 0,4} ^ {+ 0,6}$ kg Nous déterminons les paramètres d'histogramme optimaux en utilisant la liste suivante:

Annonce

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h a =array([17.37, 17.06, 16.96, 16.83, 17.34, 17.45, 17.60, 17.30, 17.02, 16.73, 17.08, 17.28, 17.08, 17.21, 17.29,17.47, 16.84, 17.39, 16.95, 16.92, 17.59, 17.28, 17.31, 17.25, 17.43,17.30, 17.18, 17.26, 17.19, 17.09,16.61, 17.16, 17.17, 17.06, 17.09,16.83, 17.17, 17.06, 17.59, 17.37,17.09, 16.94, 16.76, 16.98, 16.70, 17.27, 17.48, 17.21, 16.74, 17.12,17.33, 17.15, 17.56, 17.45, 17.49,16.94, 17.28, 17.09, 17.39, 17.05, 16.97, 17.16, 17.38, 17.23, 16.87,16.84, 16.94, 16.90, 17.27, 16.93,17.25, 16.85, 17.41, 17.37, 17.50,17.13, 17.16, 17.05, 16.68, 17.56 ] ) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=80) : %s"%round(std(a),3)) print("    (n=80):%s"%round(mean(a),3)) print("     (n=40): %s"%round(std(b),3)) print("   (n=40): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

Nous obtenons:

L'écart type pour l'échantillon (n = 80): 0,24
L'espérance mathématique pour l'échantillon (n = 80): 17,158
L'écart type pour l'échantillon (n = 40): 0,202
L'espérance mathématique de l'échantillon (n = 40): 17,138
ke1 = 1,95, h1 = 0,467, ke2 = 1,917, h2 = 0,387, dke = 0,033, m = auto
ke1 = 1,918, h1 = 0,46, ke2 = 1,91, h2 = 0,386, dke = 0,008, m = fd
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = doane
ke1 = 1,918, h1 = 0,46, ke2 = 1,91, h2 = 0,386, dke = 0,008, m = scott
ke1 = 1,898, h1 = 0,455, ke2 = 1,934, h2 = 0,39, dke = 0,036, m = pierre
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = riz
ke1 = 1,95, h1 = 0,467, ke2 = 1,917, h2 = 0,387, dke = 0,033, m = sturges
ke1 = 1,831, h1 = 0,439, ke2 = 1,917, h2 = 0,387, dke = 0,086, m = sqrt

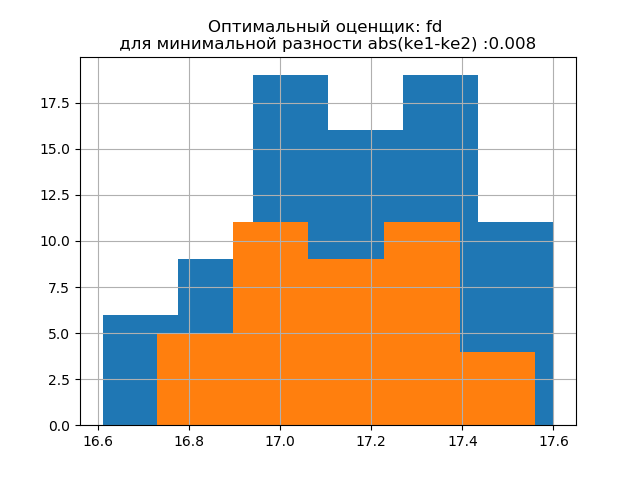
La forme de la distribution d'un grand échantillon est similaire à la forme de la distribution d'un petit échantillon. Comme il ressort du script, «fd» est un évaluateur fiable (résistant aux émissions) qui prend en compte la variabilité et la taille des données. Dans ce cas, l'erreur d'entropie du petit échantillon diminue même légèrement: h1 = 0,46, h2 = 0,386 avec une légère diminution du coefficient d'entropie de k1 = 1,918 à k2 = 1,91.

Les modèles de distribution des grands et des petits échantillons diffèrent. Comme le suggère la description, «doane» est une version améliorée du score «sturges» qui fonctionne mieux avec des ensembles de données dont la distribution n'est pas normale. Dans les deux échantillons, le coefficient d'entropie est proche de deux et la distribution est proche de la normale. L'apparition de sauts supplémentaires dans un petit échantillon sur cet histogramme, en comparaison avec le précédent, indique en outre le bon choix de l'évaluateur 'fd' .

Nous générons deux nouveaux échantillons pour la distribution normale avec les paramètres mu = 20, sigma = 0,5 et size = 100 en utilisant la relation:

 a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])

La méthode développée est applicable à l'échantillon obtenu à l'aide du programme suivant:

Annonce

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h #a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) a=array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945,20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=100):%s"%round(std(a),3)) print("    (n=100):%s"%round(mean(a),3)) print("     (n=50):%s"%round(std(b),3)) print("   (n=50): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

Nous obtenons:
L'écart type pour l'échantillon (n = 100): 0,524
L'espérance mathématique pour l'échantillon (n = 100): 19,992
L'écart type pour l'échantillon (n = 50): 0,462
L'espérance mathématique de l'échantillon (n = 50): 20,002
ke1 = 1,979, h1 = 1,037, ke2 = 2,004, h2 = 0,926, dke = 0,025, m = auto
ke1 = 1,979, h1 = 1,037, ke2 = 1,915, h2 = 0,885, dke = 0,064, m = fd
ke1 = 1,979, h1 = 1,037, ke2 = 1,804, h2 = 0,834, dke = 0,175, m = doane
ke1 = 1,943, h1 = 1,018, ke2 = 1,934, h2 = 0,894, dke = 0,009, m = scott
ke1 = 1,943, h1 = 1,018, ke2 = 1,804, h2 = 0,834, dke = 0,139, m = pierre
ke1 = 1,946, h1 = 1,02, ke2 = 1,804, h2 = 0,834, dke = 0,142, m = riz
ke1 = 1,979, h1 = 1,037, ke2 = 2,004, h2 = 0,926, dke = 0,025, m = sturges
ke1 = 1,946, h1 = 1,02, ke2 = 1,804, h2 = 0,834, dke = 0,142, m = sqrt

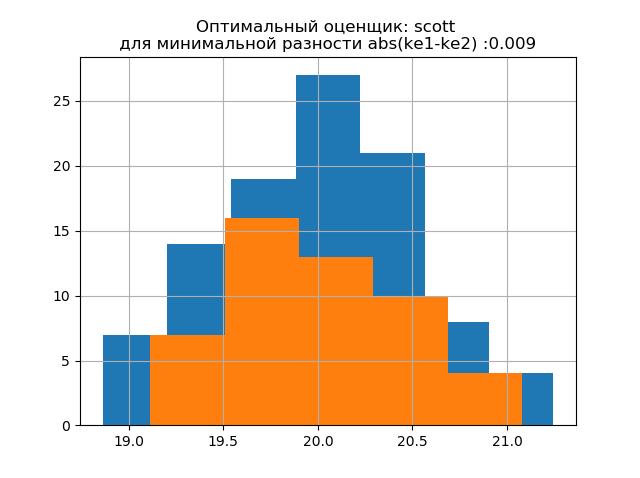
La forme de la distribution d'un grand échantillon est similaire à la forme de la distribution d'un petit échantillon. Comme il ressort de la description, «scott» est un évaluateur moins fiable qui prend en compte la variabilité et la taille des données. Dans ce cas, l'erreur d'entropie d'un petit échantillon diminue même légèrement: h1 = 1,018 et h2 = 0,894 avec une légère diminution du coefficient d'entropie de k1 = 1,943 à k2 = 1,934. . Il convient de noter que pour le nouvel échantillon, nous avons eu la même tendance à modifier les paramètres que dans l'exemple précédent.

Les modèles de distribution des grands et des petits échantillons diffèrent. Comme il ressort de la description, «doane» est une version améliorée de l'estimation «sturges» , qui fonctionne plus précisément avec des ensembles de données dont la distribution n'est pas normale. Dans les deux échantillons, la distribution est normale. L'apparition de sauts supplémentaires dans un petit échantillon sur cet histogramme par rapport au précédent indique en outre le bon choix de l'évaluateur «scott» .

L'utilisation de l'anticrénelage pour l'analyse comparative des histogrammes

Le lissage des histogrammes construits sur les grands et petits échantillons vous permet de déterminer avec plus de précision leur identité du point de vue de la conservation des informations contenues dans un plus grand échantillon. Imaginez les deux derniers histogrammes comme des fonctions de lissage:

Annonce

 from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show()

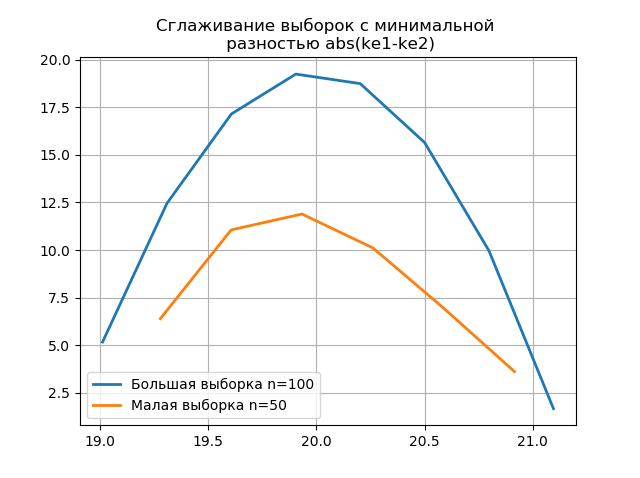
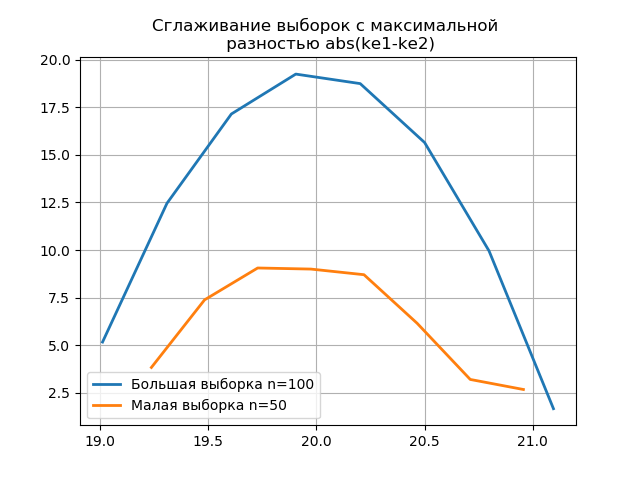
L'apparition de sauts supplémentaires dans un petit échantillon sur le graphique d'un histogramme lissé par rapport au précédent indique en outre le bon choix de l'évaluateur scott .

Conclusions

Les calculs présentés dans l'article dans la gamme de petits échantillons communs à la production ont confirmé l'efficacité de l'utilisation du coefficient d'entropie comme critère de maintien du contenu informationnel de l'échantillon tout en réduisant son volume . La technique d'utilisation de la dernière version du module numpy.histogram avec des évaluateurs intégrés est considérée - 'auto', 'fd', 'doane', 'scott', 'stone', 'rice', 'sturges', 'sqrt', qui sont tout à fait suffisants pour l'optimisation analyse des données expérimentales sur les estimations d'intervalle.

Références:

1. Hald A. Statistiques mathématiques avec applications techniques. - Moscou: maison d'édition. lit., 1956
2. Kalmykov V.V., Antonyuk F.I., Zenkin N.V.
Détermination du nombre optimal de classes de regroupement de données expérimentales pour les estimations d'intervalles // South Siberian Scientific Bulletin.- 2014. - No. 3. - P. 56-58.
3. Novitsky P. V. Le concept de la valeur d'entropie de l'erreur // Technique de mesure - 1966. - No. 7. —S. 11-14.
4.numpy.histogram - NumPy v1.16 Manual

Diminution de la taille de l'échantillon des données expérimentales sans perte d'informations

Quel est le problème des histogrammes de données expérimentales

Choix des critères d'évaluation de la qualité de l'histogramme des données expérimentales

Algorithme pour évaluer la qualité de l'histogramme des données expérimentales à l'aide du coefficient d'entropie et du module numpy.histogram

L'utilisation de l'anticrénelage pour l'analyse comparative des histogrammes

Conclusions

Références:

More articles: