Présentation

Comment savoir qu'une personne a compris ce que sont les monades? Lui-même vous en parlera dans les 5 premières minutes de communication et essaiera certainement de l'expliquer. Il rédigera également un texte à ce sujet et, si possible, le publiera quelque part, afin que tous les autres comprennent également ce que sont les monades.

Parmi les programmeurs fonctionnels, en particulier sur Haskell, les monades sont devenues un peu un mème local. Ils sont souvent tentés d'expliquer, en partant de cas particuliers et en donnant immédiatement des exemples d'utilisation. Pour cette raison, l'auditeur peut ne pas saisir l'essence principale du concept, et les monades resteront de la magie noire, ou tout simplement un moyen d'écraser les effets secondaires dans des langages purement fonctionnels.

Je vais d'abord parler des concepts de base de la théorie des catégories, puis d'un point de vue pratique, nous aborderons la définition d'une monade et verrons qu'en fait, de nombreux programmeurs utilisent cette puissante abstraction dans l'une de ses manifestations.

Ma présentation est largement basée sur le livre de Bartosz Milewski, Category Theory for Programmers, qui a été créé comme une série d’ articles de blog , est disponible en PDF et a récemment été publié sur papier.

Les exemples sont fournis dans Haskell, on suppose que le lecteur est familier avec la syntaxe et les concepts de base du langage. Dans le livre mentionné, il existe des exemples en C ++, vous pouvez comparer la pureté et l'intelligibilité du code.

Les catégories

Définition

Les catégories elles-mêmes sont des constructions très simples. Une catégorie est une collection d' objets et de morphismes entre eux. Les morphismes peuvent être considérés comme des flèches unidirectionnelles reliant des objets. Dans le cas général, on ne sait rien de l'essence des objets eux-mêmes. La théorie des catégories ne fonctionne pas avec les objets, mais avec les morphismes, ou plutôt avec leur composition .

La notation suivante est utilisée:

• Ob _C - objets de catégorie C ;
• Hom _C (A, B) - morphismes de A à B;
• g ∘ f est la composition des morphismes f et g.

Lors de la définition d'une catégorie, les morphismes sont soumis à des restrictions supplémentaires:

1. Pour une paire de morphismes f et g, si f est un morphisme de A à B (f ∈ Hom (A, B)), g est un morphisme de B à C (g ∈ Hom (B, C)), alors il existe une composition g ∘ f est un morphisme de A à C (g ∘ f ∈ Hom (A, C)).
2. Pour chaque objet, un morphisme d'identité id _A ∈ Hom (A, A) est donné.

Il existe deux propriétés importantes que toute catégorie doit satisfaire (axiomes de la théorie des catégories):

1. L'associativité de la composition: h ∘ (g ∘ f) = (h ∘ g) ∘ f;
2. Composition au morphisme identitaire: si f ∈ Hom (A, B), alors f ∘ id _A = id _B ∘ f = f.

Les catégories sont très facilement et naturellement visualisées sous forme de graphiques dirigés. En principe, tout graphe orienté peut être étendu à une catégorie en ajoutant des compositions de morphismes et de morphismes identiques, si nécessaire.

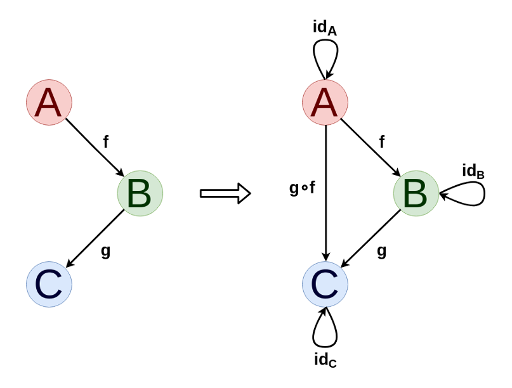
Pour n'importe quelle catégorie, vous pouvez définir une double catégorie (notée C ^op , dans laquelle les morphismes sont obtenus en tournant les flèches de la catégorie d'origine et les objets sont les mêmes. Cela nous permet de formuler des énoncés et des théorèmes doubles, dont la vérité ne change pas lorsque les flèches sont inversées.

Les objets et les morphismes ne forment pas nécessairement des ensembles (au sens classique, de la théorie des ensembles), par conséquent, dans le cas général, l'expression "classe d'objets" est utilisée. Les catégories dans lesquelles les classes d'objets et les morphismes sont encore définis sont appelées petites catégories . De plus, nous ne travaillerons qu'avec eux.

Types et fonctions

, Haskell, — . , Int Bool — , Int -> Bool — .

id, :

id :: a -> a
id x = x

— , Haskell :

f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : Hom_C(A, B) ∈ C. , a -> b — Haskell.

.

Void, ( ). absurd, , , Void, :

absurd :: Void -> a

Unit, — , (). unit , :

unit :: a -> Unit
unit _ = ()

— Bool:

data Bool = True | False

, Void, Unit Bool.

Void , absurd, Bool, Unit. , Void, , .

Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:

true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 2²ⁿ): id, true false, , not:

not :: Bool -> Bool
not True = False
not False = True

, :

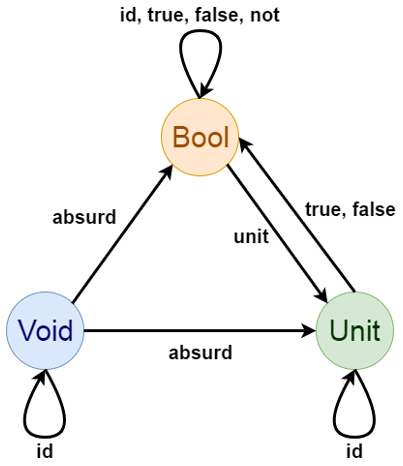
Haskell- .

— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.

, " " :

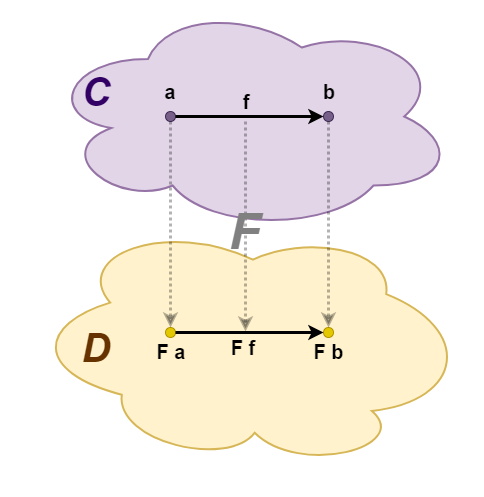
1. h = g ∘ f, F h = F g ∘ F f.
2. id_a — a, F id_a = id_{F a} — F a.

, "" : , , . , , () . , .

. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . Id_C, Id_D Id_E. , , .

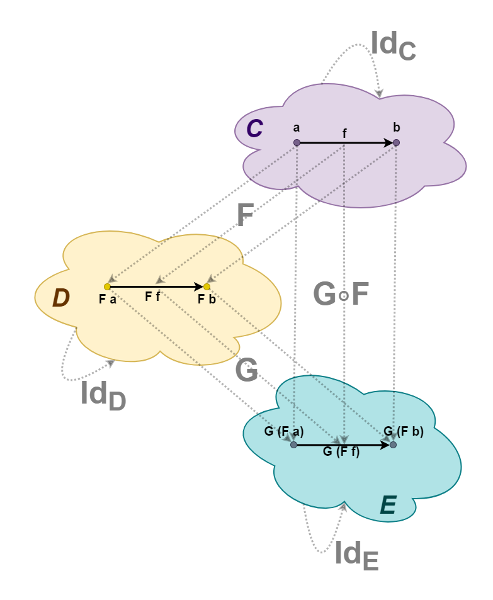
, , -, — (). , Cat ( ).

Haskell . , , - , .

Maybe , a Maybe a ( Maybe !):

data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):

--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):

class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .

, , , .. , . : , - .

. , . , , — Haskell.

: upCase, , toWords, . toUpper words:

upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:

processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".

— , . -, , , -, , .

, a , .

newtype Writer a = Writer (a, String)

, Writer — , fmap:

instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:

upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :

compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :

processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:

writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .

C m. K, , C, .. Ob_K = Ob_C. a -> b K a -> m b C: Hom_K(a, b) = Hom_C(a, m b). , , K — C.

, , , . , m — . Haskell ( Hask):

class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.

>=> . , -. a, f, , , bind:

f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:

class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:

ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :

join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:

class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:

fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))

, "" .

(.. , ) .

(a -> [b]) -> (b -> [c]) -> (a -> [c]). :

(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .

>>= :

(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :

return :: a -> [a]
return x = [x]

Monad:

instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..

, , - .

, , Maybe. Just, — Nothing. , , :

(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:

instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :

data Either a b = Left a | Right b

, . . :

type WithException a = Either String a

Maybe:

(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :

instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x

, , write-only , . a -> b , , . , , ( , ):

a -> s -> (b, s)

:

newtype State s a = State (s -> (a, s))

s , State s . runState:

runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:

instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :

(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:

instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:

get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .

, , . , , , s Unit, s -> State s Unit:

put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :

type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .