🤣 🍰 😻 États neuronaux quantiques - Représentation d'une fonction d'onde par un réseau neuronal 👻 🤖 🐅

Dans cet article, nous considérerons l'application inhabituelle des réseaux de neurones en général et des machines Boltzmann limitées en particulier pour résoudre deux problèmes complexes de la mécanique quantique - trouver l'énergie de l'état fondamental et approximer la fonction d'onde d'un système à plusieurs corps.

Nous pouvons dire qu'il s'agit d'une nouvelle version gratuite et simplifiée d'un article [2], publié dans Science en 2017 et quelques travaux ultérieurs. Je n'ai pas trouvé d'expositions scientifiques populaires de ce travail en russe (et seulement celle-ci des versions anglaises), même si cela m'a semblé très intéressant.

Concepts essentiels minimum de la mécanique quantique et du deep learning

Je veux tout de suite noter que ces définitions sont extrêmement simplifiées . Je les apporte pour ceux pour qui le problème décrit est une forêt sombre.

Un état est simplement un ensemble de quantités physiques qui décrivent un système. Par exemple, pour un électron volant dans l'espace, ce seront ses coordonnées et son élan, et pour un réseau cristallin, ce sera un ensemble de spins d'atomes situés dans ses nœuds.

La fonction d'onde du système est une fonction complexe de l'état du système. Une certaine boîte noire qui prend une entrée, par exemple, un ensemble de spins, mais renvoie un nombre complexe. La propriété principale de la fonction d'onde qui est importante pour nous est que son carré est égal à la probabilité de cet état:

P s i (s) P s i (s)^{*} = P (s)

$\ Psi (s) \ Psi (s) ^ * = P (s)$

Il est logique que le carré de la fonction d'onde soit normalisé à l'unité (et c'est aussi l'un des problèmes importants).

Espace de Hilbert - dans notre cas, une telle définition suffit - l'espace de tous les états possibles du système. Par exemple, pour un système de 40 spins pouvant prendre les valeurs +1 ou -1, l'espace de Hilbert est tout

2^{40}

$2 ^ {40}$ conditions possibles. Pour les coordonnées qui peuvent prendre des valeurs

[- i n f t y, + i n f t y]

$[- \ infty, + \ infty]$ , la dimension de l'espace de Hilbert est infinie. C'est l'énorme dimension de l'espace de Hilbert pour tout système réel qui est le principal problème qui ne permet pas de résoudre des équations analytiquement: dans le processus, il y aura des intégrales / sommations sur tout l'espace de Hilbert qui ne peuvent pas être calculées «de front». Un fait curieux: pendant toute la vie de l'Univers, vous ne pouvez rencontrer qu'une petite partie de tous les états possibles inclus dans l'espace Hilbert. Ceci est très bien illustré par une image d'un article sur Tensor Networks [1], qui représente schématiquement tout l'espace de Hilbert et les états qui peuvent être rencontrés après un polynôme à partir des caractéristiques de la complexité de l'espace (nombre de corps, particules, spins, etc.)

Une machine Boltzmann limitée - si difficile à expliquer, il s'agit d'un modèle probabiliste graphique non orienté, dont la limitation est l'indépendance conditionnelle des probabilités des nœuds d'une couche par rapport aux nœuds de la même couche. Si de manière simple, il s'agit d'un réseau de neurones avec une entrée et une couche cachée. Les valeurs de sortie des neurones dans la couche cachée peuvent être 0 ou 1. La différence avec le réseau neuronal habituel est que les sorties des neurones de la couche cachée sont des variables aléatoires sélectionnées avec une probabilité égale à la valeur de la fonction d'activation:

P_{i} (1) = s i g m a (b_{i} + s u m_{j} W_{i j} s_{j})

$P_i (1) = \ sigma (b_i + \ sum_jW_ {ij} s_j)$

où

s i g m a

$\ sigma$ - fonction d'activation sigmoïde ,

b_{i}

$b_i$ - offset pour le i-ème neurone,

W

$W$ - le poids du réseau neuronal,

s_{j}

$s_j$ - couche visible. Les machines Boltzmann limitées appartiennent aux soi-disant "modèles énergétiques", car nous pouvons exprimer la probabilité d'un état particulier d'une machine utilisant l'énergie de cette machine:

E (v, h) = - a^{T} v - b^{T} h - v^{T} W h

$E (v, h) = -a ^ Tv - b ^ Th - v ^ TWh$

où v et h sont les couches visibles et cachées, a et b sont les déplacements des couches visibles et cachées, W sont les poids. La probabilité de l'état est alors représentable sous la forme:

P (v, h) = f r a c 1 Z e^{- E (v, h)}

$P (v, h) = \ frac {1} {Z} e ^ {- E (v, h)}$

où Z est le terme de normalisation, également appelé somme statistique (il est nécessaire que la probabilité totale soit égale à l'unité).

Présentation

Aujourd’hui, les spécialistes de l’apprentissage en profondeur ont une opinion selon laquelle
Les machines Boltzmann (ci-après - OMB) est un concept dépassé qui n'est pratiquement pas applicable dans les tâches réelles. Cependant, en 2017, un article [2] paru dans Science a montré l'utilisation très efficace de l'OMB pour les problèmes de mécanique quantique.

Les auteurs ont remarqué deux faits importants qui peuvent sembler évidents, mais ils ne s'étaient jamais produits pour personne auparavant:

L'OMB est un réseau neuronal qui, selon le théorème universel de Tsybenko , peut théoriquement approximer n'importe quelle fonction avec une précision arbitrairement élevée (il y a encore beaucoup de restrictions, mais vous pouvez les ignorer).
L'OMB est un système dont la probabilité de chaque état est fonction de l'entrée (couche visible), des poids et des déplacements du réseau neuronal.

Eh bien et plus loin, les auteurs ont dit: que notre système soit complètement décrit par la fonction d'onde, qui est la racine de l'énergie OMB, et les entrées OMB sont les caractéristiques de notre état du système (coordonnées, spins, etc.):

P s i (s) = f r a c 1 Z s q r t e^{E (s, h)}

$\ Psi (s) = \ frac {1} {Z} \ sqrt {e ^ {E (s, h)}}$

où s sont les caractéristiques de l'état (par exemple, les spins), h sont les sorties de la couche cachée d'OMB, E est l'énergie d'OMB, Z est la constante de normalisation (somme statistique).

Voilà, l'article de Science est prêt, il ne reste que quelques petits détails. Par exemple, il est nécessaire de résoudre le problème de la fonction de partition non calculable en raison de la taille énorme de l'espace Hilbert. Et le théorème de Tsybenko nous dit qu'un réseau de neurones peut approximer n'importe quelle fonction, mais il ne dit pas du tout comment trouver un ensemble approprié de poids et de décalages de réseau pour cela. Eh bien, et comme d'habitude, le plaisir commence ici.

Formation modèle

Il y a maintenant quelques modifications de l'approche originale, mais je ne considérerai que l'approche de l'article original [2].

Défi

Dans notre cas, la tâche de formation sera la suivante: trouver une approximation de la fonction d'onde qui rendrait l'état d'énergie minimale le plus probable. Cela est intuitivement clair: la fonction d'onde nous donne la probabilité d'un état, la valeur propre de l'hamiltonien (l'opérateur d'énergie, ou encore plus simple, l'énergie - dans le cadre de cet article, cette compréhension suffit) car la fonction d'onde est l'énergie. Tout est simple.

En réalité, nous nous efforcerons d'optimiser une autre quantité, l'énergie dite locale, toujours supérieure ou égale à l'énergie de l'état fondamental:

E_{l o c} (s i g m a) = R e s u m_{s i g m a s i g m a^{'}} H_{s i g m a s i g m a^{'}} f r a c P s i (s i g m a^{'}) P s i (s i g m a)

$E_ {loc} (\ sigma) = Re \ sum _ {\ sigma \ sigma '} H _ {\ sigma \ sigma'} \ frac {\ Psi (\ sigma ')} {\ Psi (\ sigma)}$

ici

s i g m a

$\ sigma$ Est notre condition

s i g m a^{'}

$\ sigma '$ - tous les états possibles de l'espace de Hilbert (en réalité nous considérerons une valeur plus approximative),

H_{s i g m a s i g m a^{'}}

$H _ {\ sigma \ sigma '}$ Est l'élément matriciel de l'hamiltonien. Dépendant fortement du hamiltonien spécifique, par exemple, pour le modèle d'Ising, c'est juste

f (s i g m a)

$f (\ sigma)$ si

s i g m a = s i g m a^{'}

$\ sigma = \ sigma '$ et

- c o n s t

$-const$ dans tous les autres cas. Ne vous arrêtez pas ici maintenant; il est important que ces éléments puissent être trouvés pour divers hamiltoniens populaires.

Processus d'optimisation

Échantillonnage

Une partie importante de l'approche de l'article original était le processus d'échantillonnage. Une variation modifiée de l'algorithme Metropolis-Hastings a été utilisée. L'essentiel est:

Nous partons d'un état aléatoire.
Nous changeons le signe d'un spin choisi au hasard à l'opposé (pour les coordonnées il y a d'autres modifications, mais elles existent aussi).
Avec une probabilité égale à $P (\ sigma '| \ sigma) = \ Big | {\ frac {\ Psi (\ sigma')} {\ Psi (\ sigma)} \ Big | ^ 2$ , passez à un nouvel état.
Répétez N fois.

En conséquence, nous obtenons un ensemble d'états aléatoires sélectionnés en fonction de la distribution que notre fonction d'onde nous donne. Vous pouvez calculer les valeurs énergétiques dans chaque état et l'attente mathématique de l'énergie

m a t h b b E (E_{l o c})

$\ mathbb {E} (E_ {loc})$ .

On peut montrer que l'estimation du gradient énergétique (plus précisément, la valeur attendue de l'hamiltonien) est égale à:

G_{k} (x) = 2 * (E_{l o c} (x) - m a t h b b E (E_{l o c})) * D_{k}^{*} (x)

$G_k (x) = 2 * (E_ {loc} (x) - \ mathbb {E} (E_ {loc})) * D ^ * _ k (x)$

Conclusion

Il s'agit d'une conférence donnée par G. Carleo en 2017 pour Advanced School on Quantum Science and Quantum Technology. Il y a des entrées sur Youtube.

Dénote:

D_{k}^{*} (x) = f r a c p a r t i a l_{p_{k}} P s i (x) P s i (x)

$D ^ * _ k (x) = \ frac {\ partial_ {p_k} \ Psi (x)} {\ Psi (x)}$

Ensuite:

p a r t i a l_{p_{k}} m a t h b b E (H) =

$\ partial_ {p_k} \ mathbb {E} (H) =$

p a r t i a l f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} =

$\ partial \ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} D_{k} (x^{'}) P s i (x^{'}) s u m_{x} | P s i (x) |^{2} + f r a c s u m_{x x^{'}} P s i^{*} (x) D_{k}^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} D_k (x ') \ Psi (x')} {\ sum_x | \ Psi (x) | ^ 2} + \ frac {\ sum_ {xx '} \ Psi ^ * (x) D_k ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} -$

f r a c s u m_{x x^{'}} P s i^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | P s i (x) |^{2} f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) - D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} =

$\ frac {\ sum_ {xx '} \ Psi ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ Psi (x) | ^ 2} \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) - D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c s u m_{x x^{'}} f r a c P s i^{*} (x) P s i^{*} (x^{'}) H_{x x^{'}} D_{k} (x^{'}) | P s i (x^{'}) |^{2} + s u m_{x x^{'}} | P s i (x) |^{2} H_{x x^{'}} D_{k}^{*} (x^{'}) f r a c P s i (x^{'}) P s i (x) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ sum_ {xx '} \ frac {\ Psi ^ * (x)} {\ Psi ^ * (x')} H_ {xx '} D_k (x') | \ Psi (x ') | ^ 2 + \ sum_ {xx '} | \ Psi (x) | ^ 2H_ {xx'} D ^ * _ k (x ') \ frac {\ Psi (x')} {\ Psi (x)}} {\ sum_x | \ Psi (x) | ^ 2} -$

m a t h b b E (H) f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) + D_{k}^{*} (x)) s u m_{x} | P s i (x) |^{2} e n v i r o n

$\ mathbb {E} (H) \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) + D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2 } \ environ$

m a t h b b E (E_{l o c} D_{k}^{*}) - m a t h b b E (E_{l o c}) m a t h b b E (D_{k}^{*}) + C

$\ mathbb {E} (E_ {loc} D ^ * _ k) - \ mathbb {E} (E_ {loc}) \ mathbb {E} (D ^ * _ k) + C$

Ensuite, nous résolvons simplement le problème d'optimisation:

Nous échantillonnons les états de notre OMB.
Nous calculons l'énergie de chaque état.
Estimez le gradient.
Nous mettons à jour le poids de l'OMB.

En conséquence, le gradient énergétique tend vers zéro, la valeur énergétique diminue, tout comme le nombre de nouveaux états uniques dans le processus Metropolis-Hastings, car en échantillonnant à partir de la véritable fonction d'onde, nous obtiendrons presque toujours l'état fondamental. Intuitivement, cela semble logique.

Dans le travail d'origine, pour les petits systèmes, les valeurs de l'énergie de l'état fondamental ont été obtenues, très proches des valeurs exactes obtenues analytiquement. Une comparaison a été faite avec les approches bien connues pour trouver l'énergie de l'état fondamental, et NQS a gagné, en particulier compte tenu de la complexité de calcul relativement faible de NQS par rapport aux méthodes connues.

NetKet - une bibliothèque de l'approche "inventeurs"

L'un des auteurs de l'article original [2] avec son équipe a développé l'excellente bibliothèque NetKet [3], qui contient un noyau C très bien optimisé (à mon avis), ainsi que l'API Python, qui fonctionne avec des abstractions de haut niveau.

La bibliothèque peut être installée via pip. Les utilisateurs de Windows 10 devront utiliser le sous-système Linux pour Windows.

Considérons l'utilisation de la bibliothèque comme exemple d'une chaîne de 40 spins prenant les valeurs + -1 / 2. Nous considérerons le modèle de Heisenberg, qui prend en compte les interactions voisines.

NetKet possède une excellente documentation qui vous permet de comprendre rapidement quoi et comment faire. Il existe de nombreux modèles intégrés (dos, bosons, modèles Ising, Heisenberg, etc.), et la possibilité de décrire vous-même le modèle.

Description du décompte

Tous les modèles sont présentés sous forme de graphiques. Pour notre chaîne, le modèle Hypercube intégré avec une dimension et des conditions aux limites périodiques convient:

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

Description de Hilbert Space

Notre espace Hilbert est très simple - tous les tours peuvent prendre des valeurs +1/2 ou -1/2. Dans ce cas, le modèle intégré pour les tours est adapté:

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

Description de l'hamiltonien

Comme je l'ai déjà écrit, dans notre cas, le hamiltonien est le hamiltonien de Heisenberg pour lequel il existe un opérateur intégré:

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

Description de RBM

Dans NetKet, vous pouvez utiliser une implémentation RBM prête à l'emploi pour les tours - c'est juste notre cas. Mais en général, il y a beaucoup de voitures, vous pouvez en essayer différentes.

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

Ici, alpha est la densité des neurones dans la couche cachée. Pour 40 neurones du visible et de l'alpha 4, il y en aura 160. Il existe une autre façon d'indiquer directement par le nombre. La deuxième commande initialise les poids de manière aléatoire à partir de

N (0, s i g m a)

$N (0, \ sigma)$ . Dans notre cas, sigma est 0,01.

Samler

Un échantillonneur est un objet qui nous sera retourné par un échantillon de notre distribution, qui est donné par la fonction d'onde sur l'espace de Hilbert. Nous utiliserons l'algorithme Metropolis-Hastings décrit ci-dessus, modifié pour notre tâche:

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

Pour être précis, l'échantillonneur est un algorithme plus délicat que celui que j'ai décrit ci-dessus. Ici, nous vérifions simultanément jusqu'à 12 options en parallèle pour sélectionner le point suivant. Mais le principe, en général, est le même.

Optimiseur

Ceci décrit l'optimiseur qui sera utilisé pour mettre à jour les poids du modèle. Sur la base d'une expérience personnelle de travail avec des réseaux de neurones dans des domaines qui leur sont plus «familiers», l'option la meilleure et la plus fiable est la bonne vieille descente de gradient stochastique avec un instant (bien décrite ici ):

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

La formation

NetKet a une formation à la fois sans enseignant (notre cas) et avec un enseignant (par exemple, la soi-disant «tomographie quantique», mais c'est le sujet d'un article séparé). Nous décrivons simplement les «enseignants», et c'est tout:

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

Le Monte Carlo variationnel indique comment nous évaluons le gradient de la fonction que nous optimisons. n_smaples est la taille de l'échantillon de notre distribution que l'échantillonneur renvoie.

Résultats

Nous exécuterons le modèle comme suit:

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

La bibliothèque est construite en utilisant OpenMPI, et le script devra être exécuté comme ceci: mpirun -n 12 python Main.py (12 est le nombre de cœurs).

Les résultats que j'ai reçus sont les suivants:

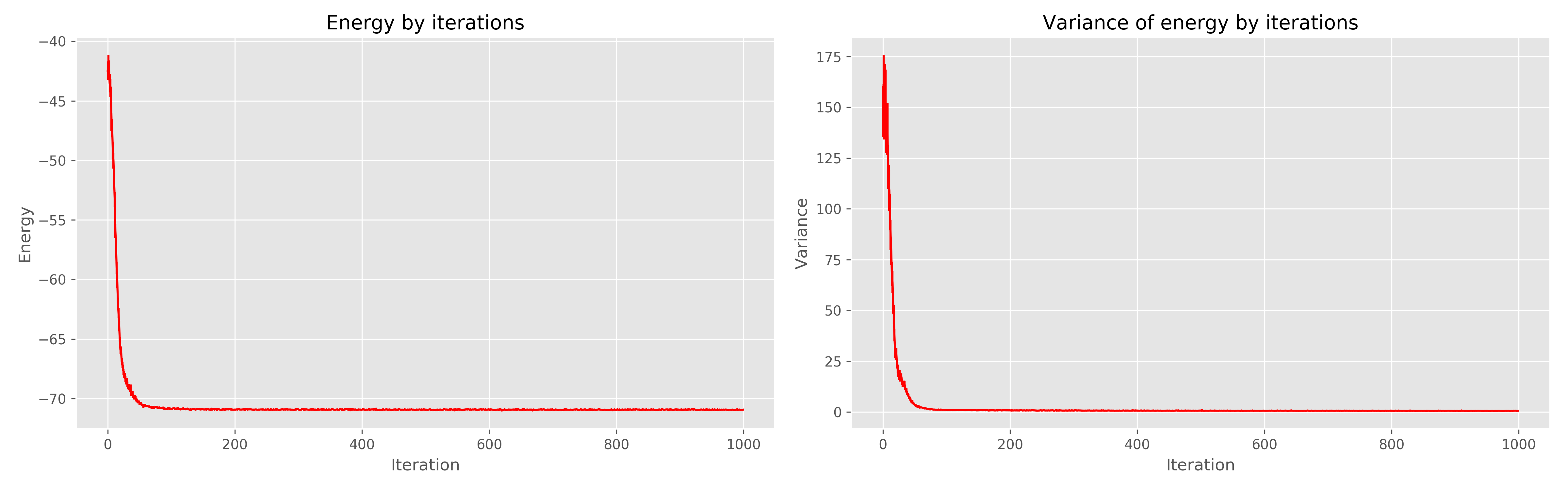
À gauche, un graphique de l'énergie de l'ère de l'apprentissage, à droite, la dispersion de l'énergie de l'ère de l'apprentissage.
On peut voir que 1000 époques sont clairement redondantes, 300 auraient suffi. En général, cela fonctionne très bien, converge rapidement.

Littérature

Orús R. Une introduction pratique aux réseaux de tenseurs: états des produits matriciels et états projetés des paires enchevêtrées // Annals of Physics. - 2014 .-- T. 349. - S. 117-158.
Carleo G., Troyer M. Résolution du problème quantique à plusieurs corps avec les réseaux de neurones artificiels // Science. - 2017. - T. 355. - Non. 6325. - Art. 602-606.
www.netket.org

États neuronaux quantiques - Représentation d'une fonction d'onde par un réseau neuronal