Catalyse des muons en termes de chimie quantique. Partie II: électronique vs liaison chimique muon

Mnogabukaff que la chimie quantique pense au principe de la catalyse muonique: comment exactement le muon abaisse la température du plasma souhaité. En deux parties (la première partie peut être lue ici ).

L'essence de la deuxième partie est simple: le muon est plus lourd que l'électron, il fournit donc une liaison chimique plus forte et une approche plus proche des noyaux, abaissant ainsi la température plasmatique requise pour déclencher la réaction thermonucléaire.

Mais ceux qui veulent regarder les formules, les graphiques et voir l'essence conceptuelle de la chimie quantique appliquée aux molécules (quasi) les plus simples sont les bienvenus sous cat.

Présentation

Dans la première partie (voir ici ) nous avons examiné la différence entre un atome d'hydrogène $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ de son homologue de muons lourds $$$\ mathrm {p} ^ + \ mu ^ -$ : dans le second cas, le muon sera lié plus fortement, et il se trouvera à une distance plus proche du proton. Dans le même temps, nous avons examiné certaines choses importantes dont nous aurons besoin ici (formes d'orbitales et système atomique d'unités).

Dans la deuxième partie (c'est-à-dire ici), nous essaierons de comprendre pourquoi, comment et dans quelle mesure la température du plasma nécessaire pour déclencher la réaction thermonucléaire diminuera. Les réactions qui nous intéressent sont:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {nouveaux noyaux + énergie}$$

où n, m = 1,2,3 correspondent respectivement au proton, au deutérium et au tritium. Naturellement, ces noyaux ont une charge positive, donc si vous essayez de les rapprocher, ils commenceront à se repousser conformément à la loi de Coulomb (voir la partie précédente ), et c'est la barrière même qui empêche le début des réactions de fusion. Soit dit en passant, dans le cas des réactions de désintégration nucléaire, cette répulsion a le rôle inverse, car après la séparation du noyau commun, les fragments, se repoussant les uns les autres, acquièrent une énergie cinétique supplémentaire, et c'est cette énergie qui est chauffée dans les centrales nucléaires.

Pour surmonter cette barrière de Coulomb, une augmentation de la température du plasma ( T ) est nécessaire, qui, comme tout le monde se souvient du cours scolaire de MKT , est associée à la vitesse moyenne des particules dans le plasma ( v ) par la formule

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

où m est la masse de particules, et $$$k_ \ mathrm {B}$ - Constante de Boltzmann .

Mais imaginons que nous avons combiné deux noyaux d'hydrogène en une certaine particule, où ils sont déjà situés à proximité, et donc le reste de la barrière pour eux est déjà très petit. Ensuite, nous aurions besoin d'accélérer considérablement ces particules (lire: nous avons besoin de températures plus basses) afin de les combiner en quelque chose de nouveau. Et juste un tel rôle devrait jouer un ion intermédiaire $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}) ^ +$ , un analogue de l'ion d'une molécule d'hydrogène $$$\ mathrm {H} _2 ^ + = (\ mathrm {He ^ -H}) ^ +$ .
Après avoir examiné les différences entre ces deux particules, nous réaliserons à quel point le muon est efficace pour abaisser la température d'inflammation de la fusion thermonucléaire.

LAIT MO MO LKAO

Nous avons donc notre système moléculaire, composé de 2 noyaux d'hydrogène avec une charge + e (un modulo de charge d'électrons) et une particule (électron ou muon) avec une charge - e . Notre système, jusqu'à ce qu'il entre en collision avec d'autres particules, est isolé, et donc son énergie peut être décomposée en ses parties constituantes:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ underbrace {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1 \ text {from} H_2}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

où les deux premiers termes ( $$$T (\ mathrm {H} _1)$ et $$$T (\ mathrm {H} _2)$ ) Est l'énergie cinétique des noyaux d'hydrogène, le troisième terme ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) Est l'énergie cinétique d'une particule négative (électron ou muon), le quatrième terme $$$V (\ mathrm {H_1 \ text {from} H_2})$ C'est l'énergie de la répulsion coulombienne des hydrogènes les uns des autres, et les deux autres sont l'attraction coulombienne de l'électron / muon pour chacun des protons. Dans le cas général, il s'agit d'un problème à 3 corps, juste un problème quantique. Naturellement, le résoudre dans le front est très difficile. Mais, heureusement, les noyaux sont au moins 1800 fois plus lourds que l'électron et 10 plus lourds que le muon, ils se déplaceront donc nettement plus lentement que les petites particules négatives. Pour cette raison, vous pouvez d'abord résoudre le problème tour à tour: d'abord, trouvez l'énergie des mouvements qui ne sont pas liés au mouvement des noyaux, c'est-à-dire $$$E_ \ mathrm {e}$ puis pleine énergie. Cela ressemble à ceci.

1. L'arrangement des noyaux d'hydrogène les uns par rapport aux autres est sélectionné, ce qui détermine les interactions coulombiennes entre eux et avec l'électron / muon. Potentiel de Coulomb $$$V (R) = k \ frac {q_1q_2} {R}$ ne dépend que des charges de particules $$$q_i$ et la distance entre eux, donc pour tous les isotopes de l'hydrogène, cette valeur sera la même. De plus, le problème du mouvement d'un électron / muon dans le champ de ces noyaux est résolu. C'est la tâche d'un seul organisme.
2. Ces énergies $$$E_ \ mathrm {e}$ sont calculés pour toutes les dispositions possibles des noyaux les uns par rapport aux autres, et ce sera l'énergie potentielle effective du mouvement des noyaux. Dans notre cas, nous devons calculer les énergies à différentes distances les unes des autres, de sorte que le potentiel pour une paire de noyaux est toujours unidimensionnel. Eh bien, nous n'avons qu'à résoudre le problème à deux corps du mouvement de deux isotopes d'hydrogène l'un par rapport à l'autre.

De toute évidence, la racine du problème avec nous est le calcul de l'énergie électron / muon dans le domaine des noyaux $$$E_ \ mathrm {e}$ . En fait, c'est le lien chimique: un certain potentiel qui maintient les noyaux ensemble à certains endroits. Et cette tâche même de trouver l'énergie de la liaison chimique est la principale de la chimie quantique.

Malheureusement, à la fois le muon et l'électron sont des particules quantiques, donc, pour trouver cette énergie, nous devons recourir aux méthodes de la mécanique quantique. En fait, notre problème du mouvement d'un électron / muon dans le domaine de deux noyaux identiques est résolu explicitement (voir ici ), mais cette solution est très compliquée et le résultat n'est pas aussi clair que dans le cas d'un atome d'hydrogène. Par conséquent, nous essaierons de démonter une approche différente et approximative, applicable à tous les systèmes. C'est ce qu'on appelle méthode des orbitales moléculaires sous forme de combinaisons linéaires d'orbitales atomiques, ou MO LKAO.

Examinons de plus près l'équation de Schrödinger pour le mouvement d'un électron / muon dans le domaine des noyaux d'hydrogène:

$$

$$\ hat {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} {\ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2})} ^ {\ hat {T}} + \ overbrace {- \ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ droite)} _ {\ hat {H}} \ psi = E \ psi$$

Cette équation a été écrite dans le système atomique d'unités (voir PS dans la partie précédente ), par conséquent, la charge du noyau d'hydrogène et de l'électron / muon est respectivement +1, --1, la masse électronique est m = 1, et pour le muon m ≈207.

Et si vous regardez de plus près, vous pouvez voir que dans l'hamiltonien, vous pouvez sélectionner une pièce liée uniquement au mouvement d'une particule négative autour d'un seul des noyaux, qui n'est que l'hamiltonien de l'atome d'hydrogène, et cela peut être fait de 2 manières:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

En dehors de l'hamiltonien d'un atome d'hydrogène ( $$$\ hat {H} _i, \ i = $ 1.$ ) nous avons toujours 2 morceaux: l'énergie d'interaction d'un électron / muon avec un autre noyau ( $$$\ hat {V} _j$ ) et l'énergie de répulsion nucléaire ( $$$\ hat {V} _ \ mathrm {HH}$ ) Le second d'entre eux n'affecte pas du tout le mouvement des électrons - c'est juste un changement d'énergie d'une certaine quantité, mais l'interaction d'un électron avec un autre noyau est une chose importante.
Nous pouvons imaginer qu'à tout moment notre particule ne tourne que autour d'un des noyaux, et l'interaction avec le second n'est qu'une correction. En tant que méthode de rotation autour de l'un des noyaux, nous pouvons supposer que l'électron / muon est dans l'état fondamental (1s), dont la fonction d'onde est bien connue de la partie précédente:

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left (- \ frac {R} {R_1} \ right)$$

où $$$R_1$ Est le rayon de Bohr pour une particule. Dans le cas d'un électron $$$R_1 = 1$ Bore (qui est le rayon de Bohr pour un électron, égal à environ 0,5 angströms), et dans le cas d'un muon $$$R_1 = \ frac {1} {m_ \ mu} \ approx \ frac {1} {207}$ .
Afin d'approximer en quelque sorte la fonction d'onde électron / muon dans le domaine de 2 noyaux, nous pouvons essayer de prendre la représentation suivante:

$$

$$\ psi \ environ c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

puis le problème de la résolution d'une équation différentielle partielle complexe avec nous est réduit à la recherche de 2 coefficients inconnus c ₁ et c ₂ . Il s'agit de l'orbitale très moléculaire présentée comme la somme des orbitales atomiques 1s des coefficients (une combinaison linéaire des scientifiques).

Naturellement, nous avons besoin d'une équation pour ces paramètres. Et l'obtenir est assez simple si vous remplacez cette approximation par l'équation de Schrödinger $$$\ hat {H} \ psi = E \ psi$ :

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

En fait, nous voulons que ce rapport soit satisfait partout, afin que nous puissions en quelque sorte calculer les valeurs moyennes de tout cela. On multiplie cette équation à gauche par $$$<1s_1 |$ et $$$<1s_2 |$ et intégrer sur toutes les coordonnées. On obtient ainsi un système de 2 équations linéaires, où il faut trouver les coefficients c ₁ , c ₂ et l'énergie E :

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Quiconque a étudié l'algèbre linéaire reconnaîtra un problème généralisé de vecteur propre-valeur propre. Avant de le résoudre, nous analyserons ce à quoi les éléments des 2 matrices, les tuta existants, sont égaux (et en même temps nous introduisons leur désignation courte avec une lettre).

• Commençons par le plus simple: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - c'est la normalisation des fonctions d'onde, et comme nous le rappelons, la probabilité totale de trouver un électron / muon est d'au moins 1 quelque part.
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - c'est ce qu'on appelle chevauchement intégral, montrant comment les nuages ​​d'électrons se chevauchent pour chacun des atomes.
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ . Cette intégrale se compose de plusieurs parties:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ . Ici, c'est similaire:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \ chapeau {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  c'est-à-dire l'énergie d'un atome d'hydrogène et la répulsion internucléaire, mise à l'échelle par l'intégrale de chevauchement (premier et dernier termes), et, pour ainsi dire, l'énergie de l'électron / muon sautant d'un atome à l'autre.
  

Trouvons les expressions des énergies de notre ion hydrogène à partir de l'équation réécrite comme

$$

$$\ begin {pmatrix} \ alpha & \ beta \\ \ beta & \ alpha \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} 1 & S \\ S & 1 \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

Pour trouver l'énergie dont vous avez besoin pour résoudre l'équation:

$$

$$\ det \ begin {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ alpha -E \ end {pmatrix} = (\ alpha -E) ^ 2 - (\ beta - ES) ^ 2 = 0$$

où "det" désigne le déterminant (déterminant d'une matrice, en russe).

Les solutions de cette équation quadratique par rapport à E sont:

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

La première pièce est évidemment l'énergie de l'atome, la seconde est la répulsion internucléaire, la même barrière coulombienne qui empêche l'inflammation de la réaction thermonucléaire, et la dernière structure complexe doit être traitée.

Si nous rejetons la répulsion internucléaire, qui n'est qu'un point de référence pour l'énergie électron / muon, nous obtenons que nous avons deux états avec l'énergie

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

Étant donné que les deux fonctions d'onde $$$| 1s_1 \ rangle$ et $$$| 1s_2 \ rangle$ - positif, et $$$\ chapeau {V} _i <0$ (parce que la particule négative est toujours attirée par le positif), alors $$$\ epsilon_ + <- \ frac {m} {2}$ (énergie d'un seul atome), et $$$\ epsilon _-> - \ frac {m} {2}$ , c'est-à-dire nous obtenons une image standard des orbitales moléculaires:



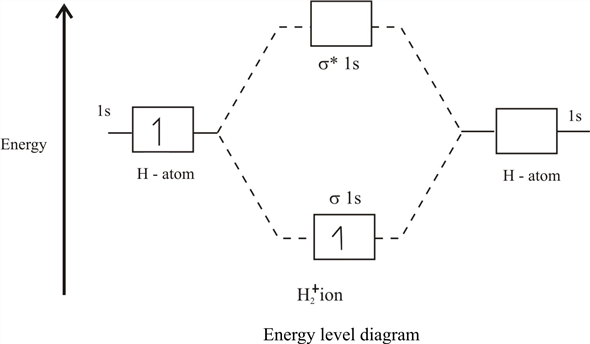
Orbitale inférieure avec énergie $$$E _ +$ appelé reliure, et le haut (avec de l'énergie $$$E _-$ ) - anti-liant ou desserrant. En conséquence, si un électron / muon se trouve sur l'orbitale moléculaire inférieure, il profite de voler autour de 2 noyaux par rapport à un, et avec son mouvement, il abaisse l'énergie totale du système. Et c'est le lien chimique très magique qui filtre la répulsion internucléaire, permettant aux noyaux d'être côte à côte pendant un certain temps.

Et ici, les intégrales de la liaison chimique doivent être calculées afin de comprendre à quel point les noyaux d'hydrogène peuvent être proches. En fait, les trois intégrales recherchées sont calculées analytiquement, mais elles sont terriblement hémorroïdaires et compliquées (pour toute personne intéressée, voir le chapitre 9 du livre de Flary sur la chimie quantique ). Par conséquent, nous irons d'une manière différente, plus simple, et calculerons ces intégrales numériquement en utilisant la méthode de Monte Carlo.

Méthode Metropolis

Je trouve cela très logique dans le texte sur l'énergie thermonucléaire de rendre hommage à son grand-père: l'atome militaire, et plus précisément le projet Manhattan . C'est à partir de lui que la méthode Monte Carlo s'est développée, et en particulier l'algorithme Metropolis , dont l'un des auteurs, Edward Teller, est le «père de la bombe à hydrogène» (c'est-à-dire la personne qui a lancé la fusion thermonucléaire sur l'atoll Envetok).


En général, nous analyserons l'essence de la méthode. Il est destiné aux tâches de mécanique statistique. La distribution principale est la distribution de Boltzmann: la probabilité de détecter un système dans un certain état est $$$\ exp (- \ beta E)$ , $$$\ beta ^ {- 1} = k_ \ mathrm {B} T$ . Et la valeur observée d'un paramètre A pour le système en équilibre thermodynamique est égale à l'intégrale

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

où q est les coordonnées qui paramètrent l'état du système (par exemple, les coordonnées / impulsions des particules), et Z est le facteur de normalisation appelé fonction de partition:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

S'il y a trop de particules dans le système, il n'est pas réaliste de compter aucune des intégrales dans le front. La méthode naïve de Monte-Carlo, dans laquelle nous sélectionnons simplement un tas de coordonnées q aléatoires, ne donnera également rien de significatif s'il existe des états vraiment possibles du système pour lesquels la probabilité $$$\ exp (- \ beta E)$ sensiblement non nul, très peu. Et c'est précisément pour de tels cas que nous avons besoin d'un échantillon par signification, dans lequel nous ne permettons à l'algorithme d'échantillonner que des endroits suffisamment probables dans l'espace d'état.

L'algorithme Metropolis se présente comme suit.

1. Lors du lancement de la simulation, nous sélectionnons une approximation de départ dans l'espace de configuration $$$\ mathbf {q} ^ {(0)}$ et un vecteur de l'incrément maximum possible $$$\ delta \ mathbf {q}$ . Au point de départ, nous calculons l'énergie du système $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (lire - probabilité $$$p = \ exp (- \ beta E ^ {(0)})$ )
2. La nouvelle configuration à la nième étape est la suivante.
   
   1. Calculez l'énergie de la configuration d'essai $$$E_ \ mathrm {trial} = E (\ mathbf {q} _ \ mathrm {trial})$ (c.-à-d. probabilité $$$p_ \ mathrm {trial} = \ exp (- \ beta E_ \ mathrm {trial})$ )
   2. Et puis on compare l'ancienne probabilité $$$p ^ {(n)}$ avec essai $$$p_ \ mathrm {trial}$
      
      
      • si la nouvelle configuration a une probabilité supérieure ou identique ( $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} \ geq 1$ ), ou, de manière équivalente, l'énergie du nouveau point est inférieure ou identique à celle de l'ancien ( $$$E_ \ mathrm {trial} \ leq E ^ {(n)}$ ), le nouveau point est accepté et le système y entre ( $$$q ^ {(n + 1)} = q_ \ mathrm {trial}$ ),
      • si la configuration d'essai est plus élevée en énergie ( $$$E_ \ mathrm {trial}> E ^ {(n)}$ ), ce qui est équivalent $$$\ frac {p_ \ mathrm {trial}} {p ^ {(n)}} <1$ , dans ce cas, nous générons un nombre aléatoire $$$P \ in [0; 1)$ à partir d'une distribution uniforme, et la comparer avec le rapport des probabilités, qui sont les probabilités de transition. Si $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ , alors nous acceptons un nouveau point, et sinon ( $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {(n)}}$ ), puis nous rejetons, et le système reste dans l'ancienne configuration ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. En suivant de nombreuses étapes selon l'algorithme ci-dessus, nous échantillonnons une partie importante (c'est-à-dire vraiment importante) de l'espace possible des configurations du système. L'intégrale qui nous intéresse est calculée par la formule:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

C'est ainsi que fonctionne l'algorithme Metropolis.

Et maintenant il faudrait l'adapter au calcul des 3 intégrales qui nous intéressent. Examinons-les plus en détail.

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}} ^ {p (\ mathbf {r})} dx dy dz$ où $$$\ mathbf {r} = (x, y, z) ^ \ mathbf {T}$ - coordonnées électron / muon, $$$\ mathbf {r} _i = (x_i, y_i, z_i) ^ \ mathbf {T}$ Sont les coordonnées des noyaux d'hydrogène, et $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - distances entre particules positives et négatives,
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limites _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1} \ frac {1} {R_2} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limites _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_2)} _ {1s_2} \ frac {1} {R_1} } ^ {A (\ mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} ^ {p (\ mathbf {r})} dxdydz$

On peut voir que, si nous calculons la fonction 1s de l'un des atomes pour la probabilité p ,


alors tout le reste sous le signe de l'intégrale (la deuxième fonction d'onde et dans 2 cas sur 3 le potentiel d'attraction de l'électron / muon vers le noyau) sera une fonction dont la valeur moyenne est calculée. La seule chose qui devra être faite, contrairement au calcul habituel par la méthode Metropolis, est de redresser la normalisation des intégrales. Le fait est que la normalisation standard sera

$$

$$Z = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ exp (-m R) dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp (-m R) R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

Et nous avons besoin de normalisation pour $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ où

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ exp (-2 m R) dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp (-2m R) R ^ 2 dR = \ frac {\ pi} {m ^ 3}$$

Cela signifie que chaque intégrale calculée selon la métropole devra être multipliée par un facteur

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

Cela peut déjà être organisé sous la forme d'un certain script, par exemple, en Python (par exemple, le code est ci-dessous).


En utilisant de tels calculs, nous pouvons enfin comparer les énergies potentielles dans l'ion hydrogène $$$\ mathrm {H} _2 ^ +$ et son homologue muon.

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ contre $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

Ainsi, armé d'un script, nous pouvons calculer la surface de l'énergie potentielle de l'approche des noyaux d'hydrogène liés par un électron et un muon. Comme point de référence énergétique, nous prenons des atomes infiniment dilués les uns des autres (c'est-à-dire, $$$-m / 2$ , qui est égal au potentiel à la distance entre les noyaux $$$R = + \ infty$ )

Dans le cas d'un électron, le potentiel proche du minimum ressemble à ceci:



Le minimum se produit à une distance d'environ 2 bore (c'est-à-dire approximativement la somme de 2 rayons atomiques), et l'énergie de dissociation de la molécule en fragments est d'environ 0,06 Hartree, ce qui correspond à un chauffage à environ 20000 degrés Kelvin (ou Celsius, cela n'a pas d'importance ici). Pour convertir les énergies, je recommande d'utiliser des ressources en ligne, comme celle- ci .

Une situation similaire avec un ion hydrogène lié par voie muonale:



Étant donné que le rayon de Bohr pour l'hydrogène muon est plus petit (voir la partie précédente ), les noyaux d'hydrogène sont également environ 200 fois plus proches à l'énergie potentielle minimale. L'énergie de dégradation de cette molécule est déjà supérieure à 10 Hartree, ce qui correspond à une température de plus de trois degrés lyam ( $$$\ approx (3.2 \ cdot 10 ^ 6) ^ \ circ$ )

Pour l'inflammation, les réactions nécessitent généralement une température de l'ordre de 10 ⁸ K , soit environ 320 Hartree. Voyons à quelles distances une énergie similaire est atteinte dans le cas de l'ion divodoron ordinaire et dans le cas de sa version muon:



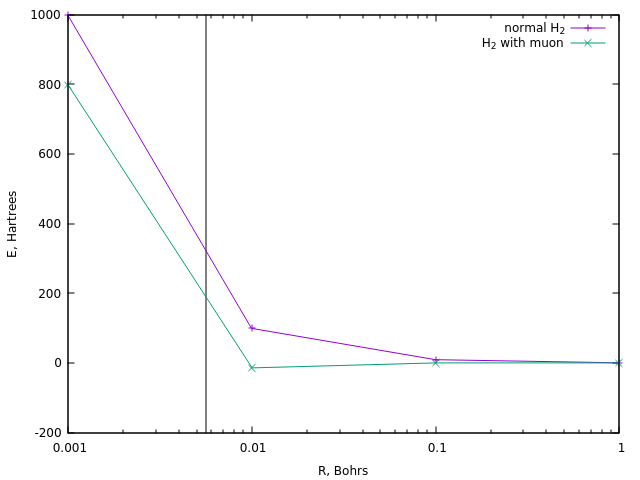
Dans le premier cas, cela correspond à une distance d'environ 0,0058 bore (ligne verticale).

Une distance similaire en hydrogène muonique est atteinte à une énergie d'environ 190 Ha, soit environ une fois et demie de moins. Et c'est l'estimation la plus simple de la température de catalyse des muons.

Mais en fait, tout sera encore plus cool. Le fait est que si une particule stable se forme $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ , alors ces noyaux, tandis que le muon est vivant, oscilleront les uns par rapport aux autres. Et ici, un effet tunnel de l'état «deux atomes d'hydrogène» à l'état «cœur plus lourd» peut se produire, et la probabilité de l'effet tunnel dépend de la longueur de effet tunnel requise d environ $$$p ^ {- d}$ , de sorte qu'en rapprochant les deux noyaux par le muon, nous augmenterons considérablement la probabilité de l'effet tunnel de cette réaction. Malheureusement, les estimations de cet effet ne nécessitent plus la chimie quantique, mais la physique nucléaire, donc cette partie de la discussion dépasse le cadre de cet article. Donc là-dessus, nous nous arrêterons.

PS Pourquoi n'est-ce pas si simple?

En fait, former ces particules n'est pas si simple dans des conditions de plasma. Le fait est que si nous heurtons deux particules, leur énergie totale dépasse évidemment l'énergie de dissociation (ou ionisation, dans le cas d'un noyau + électron / muon), donc quand elles entrent en collision, elles ne forment pas une particule stable (atome, ion, molécule), mais s'envolent par les uns les autres. Pour s'en tenir les uns aux autres, ils doivent rejeter quelque part un surplus d'énergie, et pour cela, nous avons besoin d'un troisième supplémentaire qui prendra cette énergie. Il peut s'agir d'un photon ou d'une sorte de particule gauche volant à proximité, mais l'essentiel est que les conditions contribuent à cet entraînement d'énergie excédentaire.

PPS

Si vous avez des commentaires / clarifications / questions, écrivez dans les commentaires ou dans PM. Je corrigerai tout, je répondrai et expliquerai tout.