Entrée
Au
YOW! 2013 l' un des développeurs de la langue Haskell,
prof. Philip Wadler a montré comment les monades permettent aux langages fonctionnels purs d'effectuer des opérations essentiellement impératives, telles que la gestion des entrées-sorties et des exceptions. Sans surprise, l'intérêt du public pour ce sujet a généré une croissance explosive des publications sur les monades sur Internet. Malheureusement, la plupart de ces publications utilisent des exemples écrits dans des langages fonctionnels, ce qui implique que les nouveaux arrivants en programmation fonctionnelle veulent en savoir plus sur les monades. Mais les monades ne sont pas spécifiques à Haskell ou aux langages fonctionnels, et peuvent bien être illustrées par des exemples dans les langages de programmation impératifs. C'est le but de ce guide.
En quoi ce guide est-il différent des autres? Nous allons essayer d'ouvrir les monades en moins de 15 minutes, en utilisant seulement l'intuition et quelques exemples élémentaires de code Python. Par conséquent, nous ne commencerons pas à théoriser et à nous plonger dans la philosophie, en discutant des
burritos ,
des combinaisons spatiales , des
bureaux et des endofoncteurs.
Exemples de motivation
Nous examinerons trois questions liées à la composition des fonctions. Nous les résoudrons de deux manières: l'impératif habituel et l'utilisation de monades. Ensuite, nous comparons les différentes approches.
1. Journalisation
Supposons que nous ayons trois fonctions unaires:
f1 ,
f2 et
f3 , qui prennent un nombre et le renvoient augmenté respectivement de 1, 2 et 3. Chaque fonction génère également un message, qui est un rapport sur l'opération terminée.
def f1(x): return (x + 1, str(x) + "+1") def f2(x): return (x + 2, str(x) + "+2") def f3(x): return (x + 3, str(x) + "+3")
Nous aimerions les enchaîner pour traiter le paramètre
x , en d'autres termes, nous aimerions calculer
x+1+2+3 . En outre, nous devons obtenir une explication lisible par l'homme de ce que chaque fonction a fait.
Nous pouvons obtenir le résultat dont nous avons besoin de la manière suivante:
log = "Ops:" res, log1 = f1(x) log += log1 + ";" res, log2 = f2(res) log += log2 + ";" res, log3 = f3(res) log += log3 + ";" print(res, log)
Cette solution n'est pas idéale, car elle consiste en un grand nombre de middleware monotones. Si nous voulons ajouter une nouvelle fonction à notre chaîne, nous serons obligés de répéter ce code de liaison. De plus, les manipulations avec les variables
res et
log nuisent à la lisibilité du code, ce qui rend difficile de suivre la logique principale du programme.
Idéalement, un programme devrait ressembler à une simple chaîne de fonctions, comme
f3(f2(f1(x))) . Malheureusement, les types de données renvoyés par
f1 et
f2 ne correspondent pas aux types de paramètres
f2 et
f3 . Mais nous pouvons ajouter de nouvelles fonctions à la chaîne:
def unit(x): return (x, "Ops:") def bind(t, f): res = f(t[0]) return (res[0], t[1] + res[1] + ";")
Maintenant, nous pouvons résoudre le problème comme suit:
print(bind(bind(bind(unit(x), f1), f2), f3))
Le diagramme suivant montre le processus de calcul se produisant à
x=0 . Ici
v1 ,
v2 et
v3 sont les valeurs obtenues à la suite d'appels à l'
unit et à la
bind .

La fonction
unit convertit le paramètre d'entrée
x en un tuple d'un nombre et d'une chaîne. La fonction
bind appelle la fonction qui lui est passée en paramètre et accumule le résultat dans la variable intermédiaire
t .
Nous avons pu éviter de répéter le middleware en le plaçant dans la fonction
bind . Maintenant, si nous obtenons la fonction
f4 , nous l'incluons simplement dans la chaîne:
bind(f4, bind(f3, ... ))
Et nous n'avons pas besoin d'apporter d'autres modifications.
2. Liste des valeurs intermédiaires
Nous allons également commencer cet exemple avec de simples fonctions unaires.
def f1(x): return x + 1 def f2(x): return x + 2 def f3(x): return x + 3
Comme dans l'exemple précédent, nous devons composer ces fonctions afin de calculer
x+1+2+3 . Nous devons également obtenir une liste de toutes les valeurs obtenues grâce au travail de nos fonctions, c'est-à-dire
x ,
x+1 ,
x+1+2 et
x+1+2+3 .
Contrairement à l'exemple précédent, nos fonctions sont composables, c'est-à-dire que les types de leurs paramètres d'entrée coïncident avec le type du résultat. Par conséquent, une simple chaîne
f3(f2(f1(x))) renverra le résultat final. Mais dans ce cas, nous perdons les valeurs intermédiaires.
Résolvons le problème "de front":
lst = [x] res = f1(x) lst.append(res) res = f2(res) lst.append(res) res = f3(res) lst.append(res) print(res, lst)
Malheureusement, cette solution contient également beaucoup de middleware. Et si nous décidons d'ajouter
f4 , nous devrons à nouveau répéter ce code pour obtenir la liste correcte des valeurs intermédiaires.
Par conséquent, nous ajoutons deux fonctions supplémentaires, comme dans l'exemple précédent:
def unit(x): return (x, [x]) def bind(t, f): res = f(t[0]) return (res, t[1] + [res])
Maintenant, nous réécrivons le programme comme une chaîne d'appels:
print(bind(bind(bind(unit(x), f1), f2), f3))
Le diagramme suivant montre le processus de calcul se produisant à
x=0 . Encore une fois,
v1 ,
v2 et
v3 indiquent les valeurs obtenues à partir des appels
unit et
bind .

3. Valeurs vides
Essayons de donner un exemple plus intéressant, cette fois avec des classes et des objets. Supposons que nous ayons une classe
Employee avec deux méthodes:
class Employee: def get_boss(self):
Chaque objet de la classe
Employee a un gestionnaire (un autre objet de la classe
Employee ) et un salaire, auxquels on accède par des méthodes appropriées. Les deux méthodes peuvent également renvoyer
None (l'employé n'a pas de gestionnaire, le salaire est inconnu).
Dans cet exemple, nous allons créer un programme qui montre le salaire du dirigeant de cet employé. Si le gestionnaire n'est pas trouvé ou si son salaire ne peut être déterminé, le programme renverra
None .
Idéalement, nous devons écrire quelque chose comme
print(john.get_boss().get_wage())
Mais dans ce cas, si l'une des méthodes retourne
None , notre programme se terminera avec une erreur.
Une façon évidente de gérer cette situation pourrait ressembler à ceci:
result = None if john is not None and john.get_boss() is not None and john.get_boss().get_wage() is not None: result = john.get_boss().get_wage() print(result)
Dans ce cas, nous
get_boss des appels supplémentaires aux
get_wage get_boss et
get_wage . Si ces méthodes sont suffisamment lourdes (par exemple, l'accès à la base de données), notre solution ne fonctionnera pas. Par conséquent, nous le changeons:
result = None if john is not None: boss = john.get_boss() if boss is not None: wage = boss.get_wage() if wage is not None: result = wage print(result)
Ce code est optimal en termes de calcul, mais est mal lu en raison de trois
if imbriqués. Par conséquent, nous allons essayer d'utiliser la même astuce que dans les exemples précédents. Définissez deux fonctions:
def unit(e): return e def bind(e, f): return None if e is None else f(e)
Et maintenant, nous pouvons mettre toute la solution sur une seule ligne.
print(bind(bind(unit(john), Employee.get_boss), Employee.get_wage))
Comme vous l'avez probablement déjà remarqué, dans ce cas, nous n'avons pas eu à écrire la fonction d'
unit : elle renvoie simplement le paramètre d'entrée. Mais nous allons le laisser pour qu'il nous soit alors plus facile de généraliser notre expérience.
Notez également qu'en Python, nous pouvons utiliser des méthodes en tant que fonctions, ce qui nous a permis d'écrire
Employee.get_boss(john) au lieu de
john.get_boss() .
Le diagramme suivant montre le processus de calcul lorsque John n'a pas de leader, c'est-à-dire que
john.get_boss() renvoie
None .
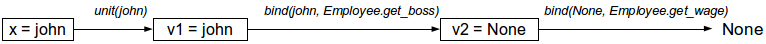
Conclusions
Supposons que nous voulons combiner les fonctions de même type
f1 ,
f2 ,
… ,
fn . Si leurs paramètres d'entrée sont les mêmes que les résultats, on peut utiliser une simple chaîne de la forme
fn(… f2(f1(x)) …) . Le diagramme suivant montre un processus de calcul généralisé avec des résultats intermédiaires, notés
v1 ,
v2 ,
… ,
vn .

Souvent, cette approche n'est pas applicable. Les types de valeurs d'entrée et de résultats de fonction peuvent varier, comme dans le premier exemple. Ou les fonctions peuvent être composables, mais nous voulons insérer une logique supplémentaire entre les appels, comme dans les exemples 2 et 3, nous avons inséré une agrégation de valeurs intermédiaires et une vérification pour une valeur vide, respectivement.
1. Décision impérative
Dans tous les exemples, nous avons d'abord utilisé l'approche la plus simple, qui peut être représentée par le diagramme suivant:

Avant d'appeler
f1 nous avons fait une initialisation. Dans le premier exemple, nous avons initialisé une variable pour stocker un journal commun, dans le second pour une liste de valeurs intermédiaires. Après cela, nous avons intercalé les appels de fonction avec un certain code de connexion: nous avons calculé les valeurs agrégées, vérifié le résultat pour
None .
2. Monades
Comme nous l'avons vu dans les exemples, les décisions impératives ont toujours souffert de verbosité, de répétition et de logique confuse. Pour obtenir un code plus élégant, nous avons utilisé un certain modèle de conception, selon lequel nous avons créé deux fonctions:
unit et
bind . Ce modèle est appelé la
monade . La fonction de
bind contient un middleware tandis que l'
unit implémente l'initialisation. Cela nous permet de simplifier la solution finale en une seule ligne:
bind(bind( ... bind(bind(unit(x), f1), f2) ... fn-1), fn)
Le processus de calcul peut être représenté par un diagramme:

Un appel à l'
unit(x) génère une valeur initiale de
v1 . Ensuite,
bind(v1, f1) génère une nouvelle valeur intermédiaire
v2 , qui est utilisée dans le prochain appel à
bind(v2, f2) . Ce processus se poursuit jusqu'à l'obtention d'un résultat final. En définissant diverses
unit et
bind dans le cadre de ce modèle, nous pouvons combiner différentes fonctions dans une même chaîne de calculs. Bibliothèques
de monades (
par exemple, PyMonad ou OSlash - environ Transl. )
Contiennent généralement des monades prêtes à l'emploi (paires d'
unit et fonctions de
bind ) pour la mise en œuvre de certaines compositions de fonctions.
Pour chaîner des fonctions, les valeurs renvoyées par
unit et
bind doivent être du même type que les paramètres d'entrée de
bind . Ce type est appelé
monadique . Selon le diagramme ci-dessus, le type de variables
v1 ,
v2 ,
… ,
vn doit être de type monadique.
Enfin, réfléchissez à la façon dont vous pouvez améliorer le code écrit à l'aide de monades. De toute évidence, les appels de
bind répétés semblent inélégants. Pour éviter cela, définissez une autre fonction externe:
def pipeline(e, *functions): for f in functions: e = bind(e, f) return e
Maintenant à la place
bind(bind(bind(bind(unit(x), f1), f2), f3), f4)
nous pouvons utiliser l'abréviation suivante:
pipeline(unit(x), f1, f2, f3, f4)
Conclusion
Les monades sont un modèle de conception simple et puissant utilisé pour composer des fonctions. Dans les langages de programmation déclarative, il aide à implémenter des mécanismes impératifs tels que la journalisation ou l'entrée / sortie. Dans les langues impératives
il permet de généraliser et de raccourcir le code qui relie une série d'appels de fonctions du même type.
Cet article ne fournit qu'une compréhension superficielle et intuitive des monades. Vous pouvez en savoir plus en contactant les sources suivantes:
- Wikipédia
- Monades en Python (avec une belle syntaxe!)
- Chronologie des tutoriels Monad