Dans un dernier article, j'ai décrit un algorithme qui vous permet de construire des itinéraires de marche plus intéressants (par opposition à plus courts, comme toutes les marques Yandex-Google) entre deux points. L'algorithme a chargé des vues, des parcs et d'autres objets agréables et intéressants pour les piétons de l'Open Street Map et a tracé un itinéraire à travers eux. En conséquence, le chemin pourrait être 10 à 20% plus long, mais beaucoup plus pittoresque et intéressant.

Photos de la ville - Alex 'Florstein' Fedorov
Dans les commentaires, beaucoup ont écrit qu'en plus des itinéraires entre deux points, ils seraient intéressés à construire des itinéraires circulaires qui commenceraient et se termineraient au même point et s'inscriraient dans un délai donné. Par exemple, si vous avez deux heures de train ou pour rencontrer des amis, vous n'aurez pas le temps d'aller quelque part loin pendant cette période, mais il est tout à fait possible de faire une promenade et de voir la beauté à proximité.
Après un certain nombre d'expériences, j'ai composé un algorithme génétique qui construit de très bonnes routes (pour moi) dans cette situation. Sous cat description du principe de fonctionnement et quelques exemples.
Ainsi, les utilisateurs veulent pouvoir faire un petit tour des environs et revenir au point de départ dans le délai spécifié (généralement 1-2 heures). Il s'est avéré que ce type de promenade est très demandé. Par exemple, l'article "Schémas de déplacement des touristes dans une destination" décrit l'étude des traces de 250 touristes à Hong Kong, tandis que 40% des touristes ont commencé à explorer la ville à partir d'un itinéraire circulaire dans un rayon de 500 mètres de l'hôtel. Cependant, souvent, les gens traînent, ne sachant pas ce qui est intéressant peut être vu à proximité.
La tâche est compliquée si ce n'est pas dans le centre touristique (où que vous alliez - vous trouverez quelque chose d'intéressant partout), mais quelque part à la périphérie où vous devez chercher des sites touristiques.
Rayon et sélection d'attractions
Pour construire un itinéraire, nous devons d'abord sélectionner les attractions que nous voulons visiter. Et pour cela, vous devez déterminer la zone de leur recherche autour du point de départ. Si l'utilisateur définit le temps de marche maximum en M minutes, le point le plus éloigné auquel vous pouvez atteindre et avoir le temps de revenir est le point à distance (V * M / 2), où V est la vitesse du piéton.
La vitesse moyenne préférée d'un piéton peut être considérée comme 1,4 mètre par seconde. Cependant, lors de visites touristiques, une personne va un peu plus lentement, car elle consacre plus de temps à une visite. J'ai construit des itinéraires autour de la ville et les ai parcourus, en comparant le moment de la promenade avec ce que l'application avait prédit. En conséquence, il s'est avéré que ma vitesse de marche moyenne était d'environ 20% inférieure, c'est-à-dire environ 1,1 m / s. Comme je m'arrêtais périodiquement pour prendre des photos, consultez la carte, parfois je traversais à nouveau la route pour choisir le meilleur angle ou acheter des glaces.

J'ai mené des expériences dans des quartiers inconnus de la ville, en utilisant mon algorithme, vous pouvez trouver toutes sortes de choses intéressantes dont je n'avais jamais entendu parler auparavant. Par exemple, un monument à la première brochure.
Le choix d'un point d'intérêt à une distance maximale conduira à la construction d'un itinéraire circulaire dégénéré. Comme le piéton n'aura plus le temps de sortir du chemin le plus court en ligne droite, il ne pourra visiter que cette attraction, y aller et revenir le long de la même rue, comme indiqué par la flèche rouge.
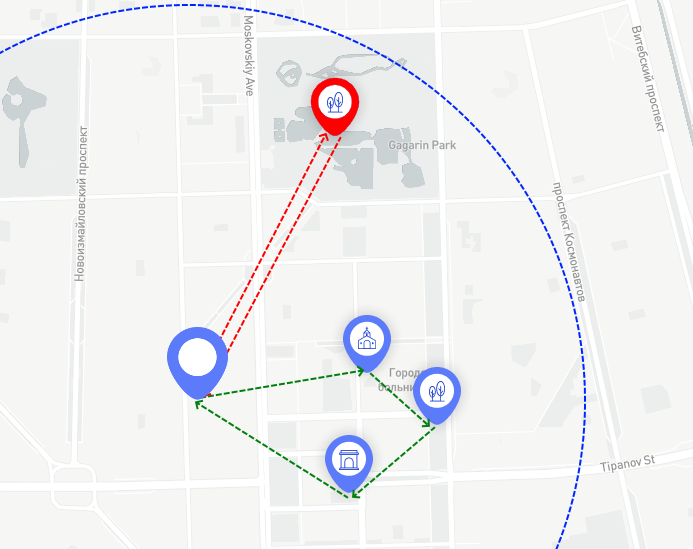
Ici, nous pouvons soit aller au parc plus loin, soit visiter plusieurs points à la fois plus près
Mais cette situation contredit l'idée de circuits circulaires intéressants, car en fait nous n'avons vu qu'une seule rue et un seul objet, mais je veux voir le plus. Par conséquent, selon les résultats des expériences, un rayon égal au tiers de la distance maximale a été choisi. Avec ce rayon de recherche, le piéton aura suffisamment de temps pour atteindre le point d'intérêt le plus éloigné le long du rayon, puis, si nécessaire, parcourra la même distance le long de l'accord à la recherche d'autres objets intéressants, puis reviendra dans le temps.
Problèmes d'approche frontale
D'accord, nous avons dressé une liste des attractions candidates. Reste maintenant à choisir lequel d'entre eux et dans quel ordre nous voulons inspecter. Très probablement, nous n'aurons pas le temps de les visiter, nous devons donc choisir le sous-ensemble le plus intéressant d'entre eux.
Tout d'abord, j'ai essayé de formuler et de construire un algorithme séquentiel simple. Cependant, j'ai rapidement rencontré un certain nombre de problèmes.
Si nous considérons la situation de la figure ci-dessus, il n'est pas clair par où commencer la construction de l'itinéraire. Si le parc est l'attraction la plus importante mais la plus éloignée, nous commencerons par une version dégénérée, dont nous avons parlé plus tôt.
La prochaine solution évidente consiste à regrouper les sites et à essayer de trouver le chemin vers le cluster le plus rentable, puis à l'intérieur. Mais là encore, tout n'est pas clair: à partir de quel cluster commencer, quelle direction prendre. Vous pouvez toujours tomber dans le piège du type où nous nous sommes trompés et avons couru dans le «désert» - une zone sans vues que nous n'avons pas assez de temps pour parcourir et revenir au point de départ.
À un moment donné, il est devenu clair pour moi que je faisais pratiquement le travail de l'algorithme génétique: je dessine différentes routes sur la carte et j'essaie de déterminer à quel point je les aimerais personnellement.
Algorithme génétique
Après avoir reçu une liste numérotée d'attractions, l'algorithme doit choisir un sous-ensemble ordonné, qui constituera la base de l'itinéraire circulaire. L'itinéraire final dans ce cas est l'un des emplacements de nombreuses attractions clés (nous ne voulons pas de répétitions et ne sommes pas tenus d'utiliser tous les objets possibles).
Connaissant la formule du nombre de placements de n à k, nous pouvons estimer le nombre possible d'options. Si nous considérons l'itinéraire d'une heure autour de la place du Palais à Saint-Pétersbourg, il y aura 54 candidats pour des attractions clés après filtrage et regroupement dans un rayon de 1320 mètres (défini comme décrit ci-dessus).
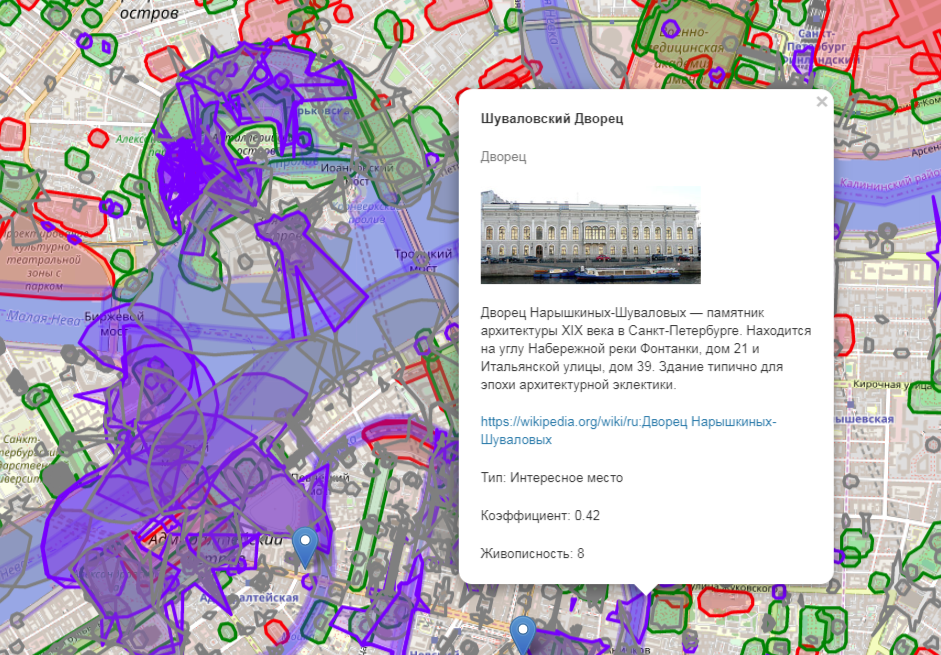
Bouillie infernale d'un tas de vues au centre, sortie de débogage des zones de visibilité calculées selon l'algorithme de l'article précédent
Le principe de sélection et de tri est décrit dans un article précédent, et nous supprimons en outre les objets ayant un intérêt inférieur à 3 (pour des objets aussi mineurs, il est peu probable qu'une personne soit prête à aller loin, sauf s'il n'y a rien d'autre à proximité). Ainsi, le nombre possible d'itinéraires peut être calculé par la formule du nombre d'emplacements de 54 à 5, il est de 379501200. Pour un itinéraire de 2 heures, dans le rayon duquel 151 points d'intérêt tombent déjà, ce nombre sera égal à 73423236600. Eh bien, c'est trop pour une simple recherche.
Chromosomes et opérateurs génétiques
Les chromosomes dans ce cas sont une ligne dans laquelle chaque élément est le numéro de l'attraction clé correspondante. Pour de telles tâches dans lesquelles les chromosomes sont des permutations ou des arrangements, il existe des variantes optimisées spéciales d'opérateurs génétiques. Ces opérateurs conservent la propriété du chromosome pour rester une permutation ou un placement de l'ensemble initial d'éléments.
- Le crossover partiellement cartographié (PMX) est utilisé pour le croisement.
- Pour la mutation, l'échange de places de deux gènes aléatoires (Swap Mutator) est utilisé.
Une description du fonctionnement de ces opérateurs avec des exemples peut être trouvée, par exemple, dans l'ouvrage "Algorithmes génétiques pour le problème du voyageur de commerce: une revue des représentations et des opérateurs".
Fonction fitness
La fonction fitness doit prendre en compte les facteurs suivants pour construire un itinéraire circulaire intéressant:
- L'intérêt total de toutes les attractions clés visitées doit être aussi grand que possible.
- Le temps de trajet total doit être aussi proche que possible de celui spécifié par l'utilisateur, l'itinéraire ne doit être ni beaucoup plus long ni beaucoup plus court. Les itinéraires courts ne sont autorisés que lorsqu'il n'y a pas suffisamment d'attractions à proximité.
- L'itinéraire ne doit pas se croiser. Pour chaque auto-intersection, nous ajoutons des pourcentages de pénalité à la valeur totale de la fonction.
- La forme de l'itinéraire doit être proche du cercle, elle doit capturer la plus grande zone possible de la ville et éviter les cas dégénérés. Pour ce faire, nous avons mis dans la fonction le rapport de l'aire de la figure décrite par l'itinéraire à l'aire du cercle dans lequel les vues ont été recherchées.
Voici un exemple d'un bon aller-retour. Il traverse deux parcs et ne visite jamais le même endroit deux fois
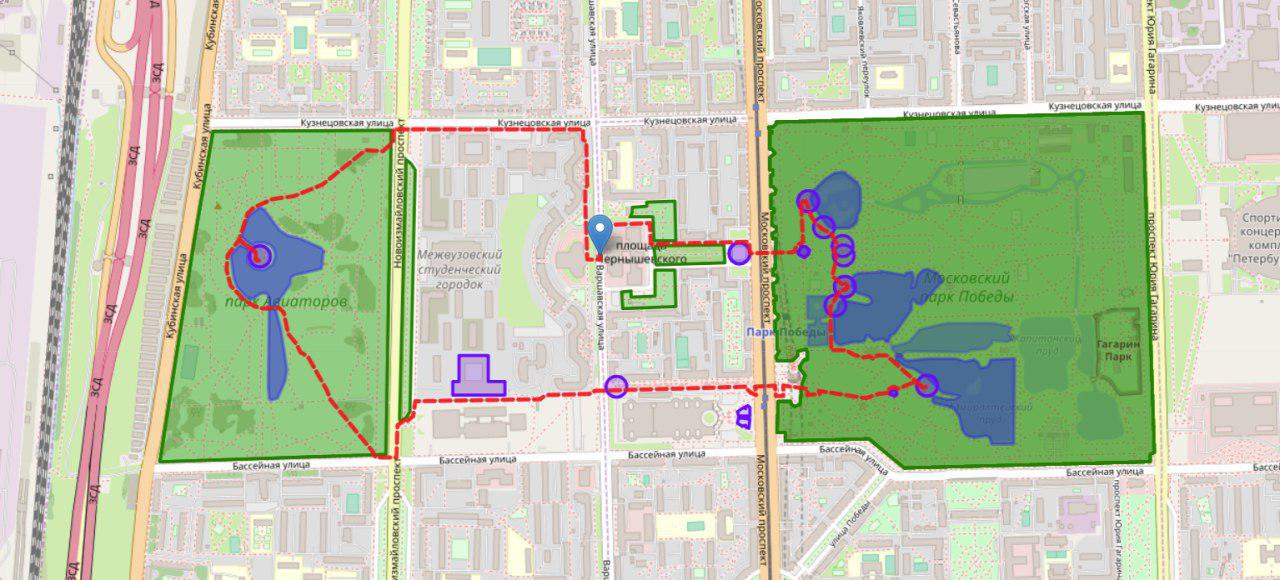
Voici un exemple d'un itinéraire clairement infructueux. Il contient des branches sans issue, où le piéton devra revenir en arrière le long du chemin examiné, et des auto-intersections. Aux intersections, le temps est généralement perdu en vain pour réexaminer des sections déjà vues de la ville.
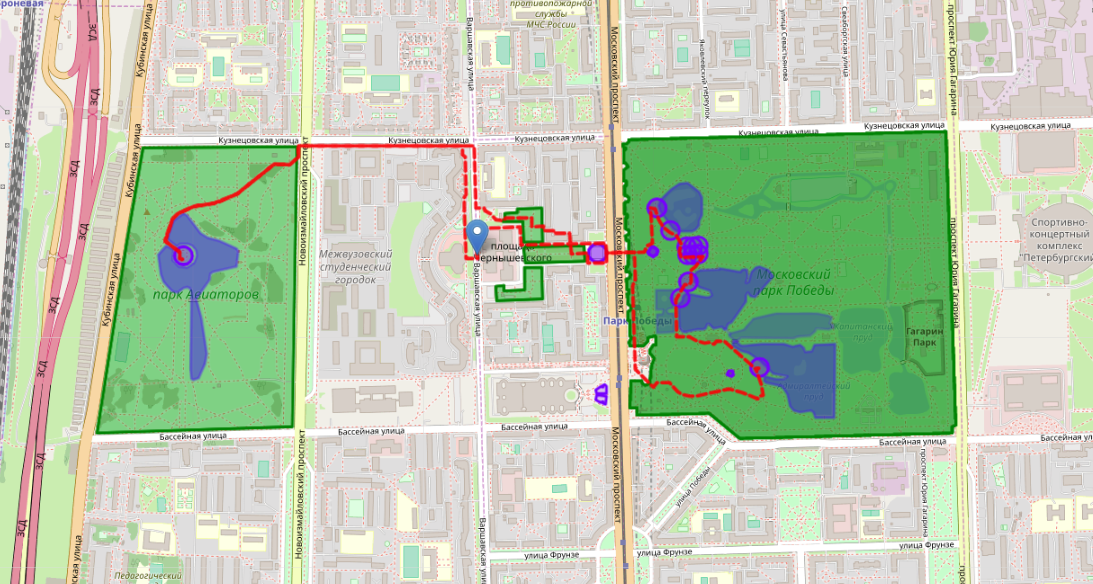
La mauvaise route a en fait été obtenue par la génétique, dans laquelle les points 3 et 4 ont été désactivés pour la fonction fitness (amendes pour auto-franchissement et pour une petite zone)
Nuances
Pendant les tests, quelques nuances supplémentaires sont apparues.
Délai dépassé
Lors des travaux de génétique, nous comptons la longueur de l'itinéraire le long de lignes droites entre des points. Et après avoir sélectionné des objets pour la communication en utilisant l'algorithme génétique, nous recherchons le chemin entre eux en utilisant l'algorithme de l'article précédent. Dans ce cas, le chemin peut devenir plus long et ramper hors du temps. Après tout, dans la ville, le chemin le plus court le long de la rue peut être plusieurs fois plus long qu'une ligne droite.
En moyenne, la différence est généralement d'environ 10 à 20% et nous l'intégrons dans la fonction fitness (c'est-à-dire que la génétique recherche une route avec une marge de temps, qui est ensuite consommée lors de la pose d'une route détaillée). Parfois, cela ne suffit pas - vous devez recalculer à nouveau l'itinéraire. Nous avons de tels endroits dans les villes où la différence entre les itinéraires «comme un oiseau» et «comme un piéton» est de kilomètres.
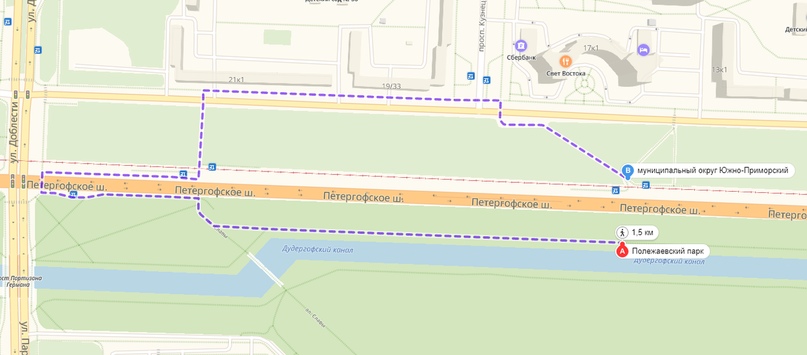
Entre les points de 50 mètres en ligne droite, mais un kilomètre et demi le long des trottoirs et des passages contournant.
Cependant, tout de même, l'algorithme dépasse parfois le temps défini par l'utilisateur, mais ici, tout le monde peut décider lui-même s'il a 10-15 minutes supplémentaires ou s'il devra terminer la marche plus tôt.
Venise
Lorsque l'algorithme était prêt, j'ai décidé d'ajouter les meilleures villes touristiques d'Europe pour le plaisir. Cela s'est avéré intéressant: les villes sont différentes partout, les fonctionnalités de la cartographie dans OSM aussi, par conséquent, j'ai dû constamment terminer quelque chose.
Plus précisément, la recherche d'itinéraires circulaires s'est interrompue à Venise. Comme il s'agit d'un exemple unique d'une ville avec des zones indépendantes - les îles sont séparées par le Grand Canal, à travers lequel il n'y a pas de ponts, la traversée n'est possible que par ferry.

En conséquence, l'algorithme a sélectionné une partie des objets d'un côté du détroit, une partie de l'autre, puis n'a pas pu trouver un chemin terrestre entre eux et est tombé. J'ai dû ajouter un contrôle sur l'accessibilité de toutes les attractions depuis le point de départ.
Parfois, vous devez toujours revenir de la même manière
Dans l'exemple avec le parc ci-dessus, il y a une partie de l'itinéraire où vous devez revenir en arrière de la même manière - c'est une petite péninsule sur laquelle se dresse un monument avec un avion. Le seul chemin mène à cette péninsule, et il faudra y revenir. De tels remboursements ne peuvent donc pas être totalement interdits. L'algorithme pour cela augmente le poids de tous les bords qui ont déjà été parcourus, réduisant la probabilité d'un retour le long d'eux, mais rend cela encore possible.
Bien que parfois cela fonctionne toujours mal. Par exemple, ils se plaignent de la cathédrale principale de Kaliningrad. Il est situé sur une île au milieu de la rivière par laquelle passe le pont. De ce pont, il y a une descente et un chemin vers la cathédrale, apparemment l'algorithme augmente trop le poids de ce seul chemin, ce qui rend le retour sur celui-ci peu rentable. En conséquence, il ne mène presque jamais à la cathédrale, bien que ce soit l'une des principales attractions de la ville. Cela nécessite encore une sorte de raffinement.
Résultats
L'algorithme génétique est un peu imprévisible, il est donc parfois bogué et dessine d'étranges zigzags. Mais en général, je suis satisfait du résultat. Ce qui est particulièrement agréable, l'algorithme fonctionne non seulement dans le centre touristique (où ce n'est pas un problème pour s'amuser), mais aussi à la périphérie de la ville. Où, souvent, sans indices, trouver quelque chose d'intéressant est très difficile.
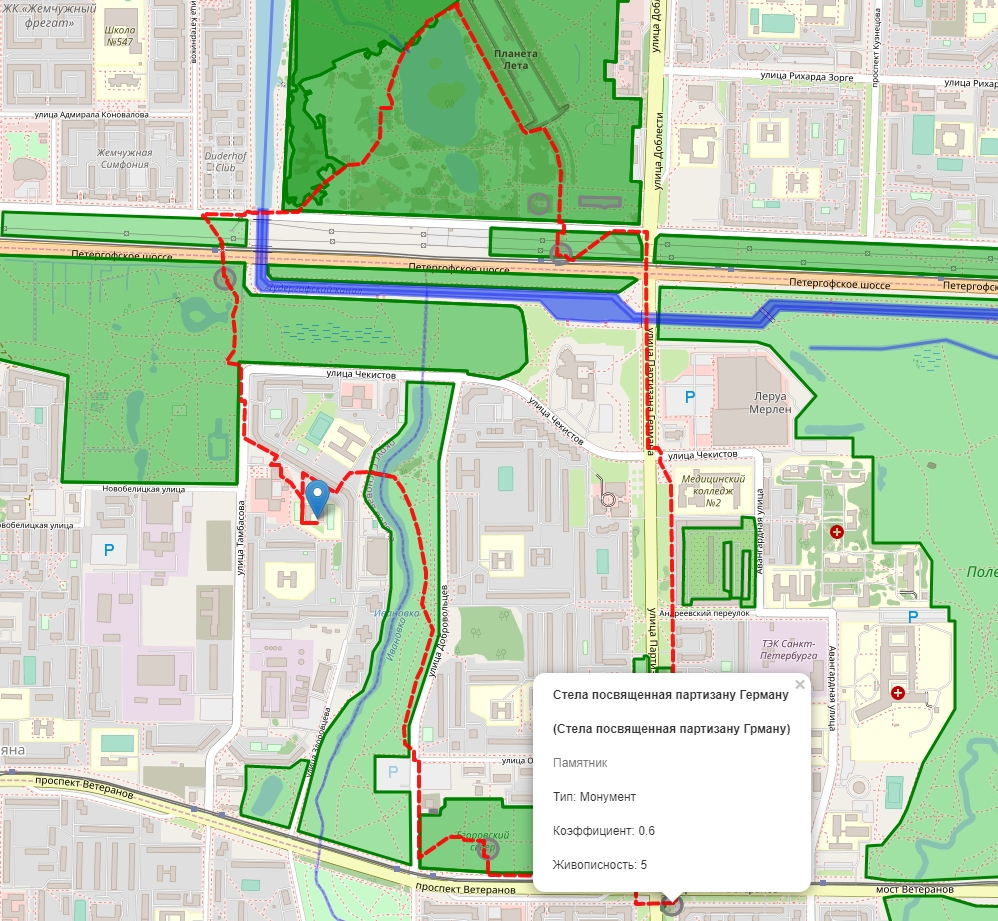
Même dans les sacs de couchage du sud-ouest de Saint-Pétersbourg, vous pouvez trouver suffisamment de monuments pour une promenade de deux heures
Vous pouvez essayer l'algorithme vous-même dans l'une des 77 villes prises en charge sur notre site Web Sight Safari ou dans notre application Android (oui, nous l'avons finalement terminé).
Il est particulièrement intéressant de voir comment l'algorithme fonctionnera dans les villes avec un terrain et des élévations complexes. Nous avons ajouté la prise en charge de l'analyse d'élévation à la bibliothèque de sondeurs Graphopper, mais nous ne pouvons pas vérifier comment cela devrait être - Peter est une ville trop plate.
En général, essayez, écrivez des avis, les itinéraires sont-ils correctement construits. Vous pouvez immédiatement demander l'ajout de nouvelles villes.