🌙 🤞🏼 🧚🏻 Types d'infinis et de tronc cérébral 🍑 🖊️ 🚶🏿

Cet article est la suite d'un article sur des nombres énormes . Mais maintenant, nous allons encore plus loin - dans l'infini de l'infini.

Pour cela, nous avons besoin de ZFC - la théorie des ensembles Zermelo, Frenkel + Choice. Le choix est l'axiome du choix, l'axiome le plus controversé de la théorie des ensembles. Elle mérite un article séparé. On suppose que vous savez quelle est la "puissance" de l'ensemble. Sinon, alors google, c'est sûr que c'est mieux que moi. Ici, je ne ferai que rappeler à certains

Faits connus

La puissance d'un ensemble d'entiers est notée par $\ aleph_0$ . Il s'agit de la première puissance infinie; ces ensembles sont appelés dénombrables.
La puissance de tout sous-ensemble infini d'entiers est simple, régulière, etc. - également dénombrable.
L'ensemble des nombres rationnels, c'est-à-dire les fractions p / q, est également dénombrable; ils peuvent être transmis par un serpent.
Pour toute puissance, il existe une opération de jeu de puissance - l'ensemble de tous les sous-jeux qui crée plus de puissance que celui d'origine. Parfois, cette opération est appelée élever un deux à une puissance, c'est-à-dire $powerset (\ aleph_0) = 2 ^ {\ aleph_0} = \ aleph_c$ . Le jeu de puissance à partir de la puissance calculée est la puissance du continuum.
La puissance du continuum est possédée par: des segments finis et infinis, des figures planes et volumétriques, et même des espaces à n dimensions dans leur ensemble
Pour les mathématiques ordinaires, la puissance suivante, $powerset (\ aleph_c)$ pratiquement pas nécessaire, généralement tout le travail se fait avec des ensembles dénombrables et des ensembles d'alimentation continue

Maintenant

Des faits peu connus

Dans ZFC, toutes les collections d'éléments ne peuvent pas être définies. Il existe des collections si vastes qu'il est impossible de les laisser se constituer; des paradoxes surgissent. En particulier, «l' ensemble de tous les ensembles » n'est pas un ensemble. Cependant, il existe des théories des ensembles où de tels ensembles sont autorisés.

Plus loin. Définir la théorie ... Quels objets? Des chiffres? Une pomme? Des oranges? Curieusement, ZFC n'a besoin d'aucun objet. Prenez l'ensemble vide {} et acceptez qu'il signifie 0. 1 désigne {{}} le diable comme {{{}}} et ainsi de suite. {5,2} est {{{{{{{{}}}}}}, {{{}}}}. En utilisant des entiers, nous pouvons en créer de vrais, et des collections de vrais peuvent créer toutes les formes.

La théorie des ensembles est donc ... comment dire ... la théorie creuse. Cette théorie n'est rien. Plus précisément, sur la façon dont vous pouvez imbriquer (imbriquer, c'est-à-dire les mettre les uns dans les autres) des accolades.

La seule opération définie dans la théorie des ensembles est

$\ in$ - un symbole d'appartenance. Mais qu'en est-il de l'unification, de l'exclusion, de l'égalité, etc.? Ce sont toutes des macros, par exemple:

$(A = B) \ equiv \ forall x ((x \ in A) = (x \ in B))$

Autrement dit, en traduction en russe, deux ensembles sont considérés comme identiques lorsque, lors du test d'un élément pour leur appartenir, nous obtiendrons les mêmes résultats

Les ensembles ne sont pas ordonnés, mais cela peut être corrigé: que la paire ordonnée (p, v) soit {{p}, {p, v}}. Inélégant du point de vue du programmeur, mais suffisant pour un mathématicien. Maintenant, l'ensemble de toutes les paires param-valeur définit une fonction, qui est maintenant également définie! Et voila! toute analyse mathématique, qui fonctionne au niveau des langages du second ordre , puisqu'elle ne parle pas de l'existence des nombres , mais de l'existence des fonctions , s'effondre dans un langage du premier ordre!

Ainsi, la théorie des ensembles est une théorie pauvre sans objets et avec une icône de relation, qui a un pouvoir absolument monstrueux - sans aucune nouvelle hypothèse, elle génère de lui-même l'arithmétique formelle, les nombres réels, l'analyse, la géométrie et bien plus encore. C'est une sorte de mathématiques TOE.

Hypothèse du continuum - CH

Y a-t-il du pouvoir entre

$\ aleph_0$ et

$2 ^ {\ aleph_0}$ ? Cantor n'a pas pu résoudre ce problème, le «roi des mathématiciens» Hilbert a loué son importance, mais ce n'est que plus tard qu'il a été prouvé que cette hypothèse ne peut être ni prouvée ni réfutée. Elle est indépendante de ZFC.

Cela signifie que vous pouvez créer deux calculs différents: l'un avec ZFC + CH, l'autre avec ZFC + (pas CH). En fait, même plus de deux. Supposons que nous rejetons CH, c'est-à-dire que nous croirons qu'entre

$\ aleph_0$ et

$2 ^ {\ aleph_0}$ il y a encore du pouvoir. Combien peut-il y en avoir? Un, deux? Godel n'en croyait qu'un seul. Mais, comme il s'est avéré, l'hypothèse qu'il y en a 2, 17, 19393493 ne conduit pas à des contradictions. N'importe quel nombre, mais pas infini!

Lorsque, dans l'arithmétique formelle, nous tombons sur une déclaration non démontrable, pour certaines raisons, nous savons que, néanmoins, cette déclaration, bien que non prouvable, est en fait soit vraie soit fausse. Dans la théorie des ensembles, cela ne fonctionne pas, nous obtenons vraiment différents mathématiciens. Comment s'y rapporter? Il existe trois approches philosophiques:

Formalisme: pourquoi, en fait, être surpris? Nous fixons les règles du jeu des symboles, des règles différentes - un résultat différent. Pas besoin de chercher un problème là où il n'existe pas

Platonisme: Mais comment expliquer alors que des théories complètement différentes, telles que ZFC et New Foundations, construites sur des principes complètement différents, donnent presque toujours le même résultat? Est-ce à dire que derrière les formules se cache une sorte de réalité que nous étudions? Cette opinion a été défendue, par exemple, par Godel

Multivers: Nous pouvons avoir de nombreux axiomatiques, donnant parfois le même résultat, parfois non. Nous devons percevoir l'image dans son ensemble - si la couleur est associée à différents systèmes d'axiomes, alors l'arbre d'effets coloré est mathématique. Si quelque chose est vrai partout - c'est blanc, mais il y a aussi des branches colorées.

De plus en plus haut.

À l'avenir, pour simplifier, nous accepterons l'hypothèse du continuum, c.-à-d.

$powerset (\ aleph_0) = \ aleph_1 = \ aleph_c$ - c'est très pratique. En fait, nous accepterons également l'axiome le plus fort, l'hypothèse du continuum généralisé selon laquelle entre x et le jeu de puissances (x), il n'y a jamais de pouvoirs intermédiaires. Maintenant, nous itérons le jeu de puissance et tout est simple:

$\ aleph_0 \ rightarrow \ aleph_1 \ rightarrow \ aleph_2 \ rightarrow ... \ rightarrow \ aleph_ {36463634} \ rightarrow$

Jusqu'où peut-on aller? Après un nombre infini d'itérations, nous arrivons à

$\ aleph_ \ omega$ - une puissance infinie dans l'ordre! À propos, son existence n'était pas évidente pour Cantor. Mais une seconde! Après tout, la fonction PowerSet est toujours définie, donc

$\ aleph_ \ omega$ ne peut pas être le dernier!

$\ aleph_ \ omega \ rightarrow \ aleph _ {\ omega + 1} \ rightarrow \ aleph _ {\ omega + 2} \ rightarrow ...$

Pour obtenir

$\ aleph _ {\ omega + 3}$ il est nécessaire de répéter l'infini et trois fois de plus . Avez-vous déjà commencé à démolir le toit? Ou bien ça le sera. Parce qu'encore une fois, après avoir répété le jeu de puissance un nombre infini de fois, nous arrivons à

$\ aleph _ {\ omega + \ omega} = \ aleph _ {\ omega2}$ , après quoi, naturellement,

$\ aleph _ {\ omega2 + 1}$

Ayant atteint l'infini un nombre infini de fois , nous obtenons l'indice

$\ oméga ^ 2$ . Comment aimez-vous ce pouvoir, par exemple:

$\ aleph _ {\ omega ^ 3 + \ omega ^ 2 + \ omega4 + 48745}$ ? Alors que nous avons répété le pouvoir sur la liste des ordinaux, voici les ordinaux initiaux:

mais il y en a beaucoup, beaucoup plus. Nous allons donc tout sauter tout de suite et le faire

Grand pas tout de suite

Attention! Ce qui est écrit ci-dessous peut être dangereux pour votre cerveau! Nous avons réitéré le nombre de puissances un nombre dénombrable de fois, mais n'agitons-nous pas dans le continuum ? Honnêtement, je suis moi-même un peu saucisse du fait que le cycle peut être effectué un continuum de fois, mais la théorie des ensembles nécessite l'existence

$\ aleph _ {\ aleph_1}$

Ensuite, nous irons plus vite:

$\ aleph _ {\ aleph_1} \ rightarrow \ aleph _ {\ aleph_2} ... \ rightarrow \ aleph _ {\ aleph_ \ omega} = \ aleph _ {\ aleph_ \ aleph} \ rightarrow$

La dernière Alef a un indice de zéro, mais le latex local ne permet pas de le mettre - il y a trop de niveaux. Mais l'essentiel est que vous compreniez, peu importe la façon dont nous créerions un nouveau pouvoir monstrueux, nous pouvons dire - oui, ce n'est qu'un répéteur , et mettre toute cette construction sous la forme d'un index du nouvel Aleph. Maintenant les capacités grandissent comme une boule de neige, on ne peut pas s'arrêter, la pyramide d'Aleph est plus haute et on peut créer n'importe quel pouvoir ... Ou pas?

Puissance inaccessible

Et s'il y a un pouvoir si grand

$\ theta$ que peu importe comment nous essayons de l'atteindre «par le bas», en construisant des structures d'Alephs, nous n'y arriverons pas? Il s'avère que l'existence d'un tel pouvoir est indépendante de ZFC. Vous pouvez accepter son existence ou non.

J'entends le murmure du rasoir d'Occam ... Non, non. Les mathématiciens adhèrent au principe opposé, qui est appelé le maximalisme ontologique - que tout ce qui est possible existe. Mais il y a au moins deux autres raisons pour lesquelles je veux accepter cette hypothèse.

Premièrement, ce n'est pas le premier pouvoir inaccessible que nous connaissons. D'abord ... c'est le pouvoir de comptage familier. Curieusement, il a toutes les propriétés inaccessibles - il n'est tout simplement pas habituel de l'appeler ainsi:
Il n'y a aucun moyen d'obtenir une puissance infinie «d'en bas» - ni en ajoutant des éléments un nombre fini de fois, ni en itérant le jeu de puissances () un nombre fini de fois, en utilisant des ensembles finis pour l'ensemencement, vous n'obtiendrez pas l'infini. Pour obtenir l'infini, vous devez déjà l'avoir quelque part.
L'existence d'une puissance infinie est introduite par un axiome spécial - l'axiome de l'infini. Sans elle, l'existence d'une puissance infinie n'est pas démontrable.

Deuxièmement: si nous rejetons l'axiome de l'infini, nous obtenons FinSet, une simple théorie des ensembles de jouets avec des ensembles finis. Écrivons tous ces ensembles (le soi-disant modèle théorique )

{}
{{}}
{{{}}, {}}
{{{{}}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}}
{{{{}}}, {{}}, {}}
...

Et nous obtenons ... un ensemble infini d'ensembles finis ... C'est-à-dire que le modèle de la théorie des ensembles finis est infini et y joue le rôle de "l'ensemble de tous les ensembles". Peut-être que cela aidera à comprendre pourquoi la théorie ne peut pas parler de «l'ensemble de tous les ensembles» - un tel ensemble existe toujours en tant que modèle en dehors de la théorie et a d'autres propriétés que les ensembles à l'intérieur. Vous ne pouvez pas ajouter l'infini à la théorie des ensembles finis.

Et oui

$\ theta$ c'est la «multitude de toutes les multitudes» de la théorie ZFC. Dans cette vidéo, à la fin, il est très joliment dit à propos de la puissance inaccessible, mais nous devons continuer.

Encore plus loin.

Bien sûr, nous pouvons aller plus loin en répétant

$powerset (\ theta)$ . Après avoir traversé toutes les étapes décrites ci-dessus, construit d'énormes tours de répétition, nous rencontrons à nouveau un cardinal inaccessible (mais maintenant nous n'avons plus besoin de nouveaux axiomes, avec l'axiome de l'existence d'un pouvoir inaccessible que nous venons d'ajouter, cela est devenu prouvable). Et encore et encore.

$\ theta_0 \ rightarrow \ theta_1 \ rightarrow \ theta_2 \ rightarrow ... \ rightarrow \ theta_ {36463634} \ rightarrow$

Notez que maintenant la flèche n'a plus de sens pour nous, comme l'exécution de la fonction Powerset (), mais GetNextInaccessible (). Sinon, tout semble très similaire, nous avons:

$\ theta _ {\ theta_1} \ rightarrow \ theta _ {\ theta_2} ... \ rightarrow \ theta _ {\ theta_ \ omega} \ rightarrow \ theta _ {\ theta_ \ theta} \ rightarrow$

Maintenant, nous allons certainement réaliser quoi que ce soit ... Ou pas?

Hiérarchie des grandes capacités.

Oui, avec GetNextInaccessible, nous rencontrons une puissance hyper inaccessible. Son existence nécessite un axiome de plus. Il existe des pouvoirs hyper-hyper-inaccessibles. Et ainsi de suite. Mais il existe d'autres façons de déterminer la puissance , non seulement par l'inaccessibilité:

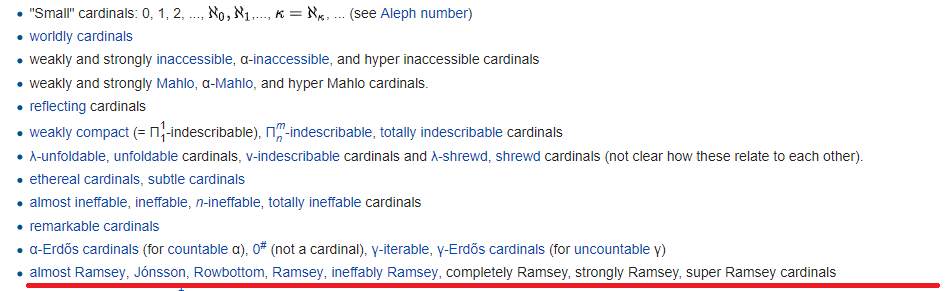
Derrière chaque lien se trouve, en règle générale, toute une hiérarchie sans fin avec un nombre arbitraire de préfixes d'hyper- et de répéteurs. Cependant, le nombre total de formules qui déterminent les cardinaux inaccessibles n'est pas si grand - car le nombre de formules est dénombrable !!! Par conséquent, tôt ou tard, ils prendront fin. Là où ils se terminent, une ligne rouge est tracée. Tout ce qui est en dessous de cette ligne est défini de manière plus instable, quoique formellement.

La ligne rouge elle-même marque la fin de l'univers de Gödel (mais n'oubliez pas que Gödel a créé DEUX univers différents) - l'univers d'ensembles construits par le bas à l'aide de formules. Les capacités au-dessus de la ligne rouge sont appelées hmm, "petites" et en dessous - grandes:

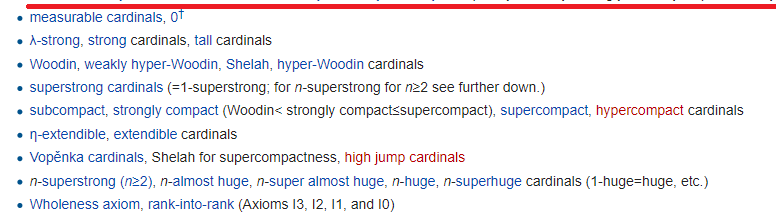
L'idée principale en eux est que l'univers des ensembles devient si grand qu'il commence à se répéter dans différents sens. Chaque ligne, comme toujours, nécessite un axiome distinct et plusieurs. Et plus intéressant encore, tout cela n'est pas aussi inutile qu'on pourrait le penser. Par exemple, l'axiome le plus fort (rang en rang), en fin de compte, est nécessaire pour prouver le fait des comprimés .

Ci-dessous une enquête, le dernier choix est décrypté ici .

Types d'infinis et de tronc cérébral