Non, bien sûr, je ne suis pas sérieux. Il doit y avoir une limite dans la mesure où il est possible de simplifier le sujet. Mais pour les premières étapes, une compréhension des concepts de base et une "entrée" rapide dans le sujet, cela peut être permis. Et comment nommer correctement ce matériel (options: «Apprentissage automatique pour les nuls», «Analyse des données des couches», «Algorithmes pour les plus petits»), nous discuterons à la fin.
Pour les entreprises. Il a écrit plusieurs programmes d'application sur MS Excel pour la visualisation et la visualisation des processus qui se produisent dans différentes méthodes d'apprentissage automatique lors de l'analyse des données. Voir, c'est croire, en fin de compte, selon les médias de la culture qui a développé la plupart de ces méthodes (en passant, en aucun cas toutes. La plus puissante "méthode du vecteur de support", ou SVM, machine à vecteur de support est une invention de notre compatriote Vladimir Vapnik, de l'Institut de gestion de Moscou. 1963, au fait! Maintenant, cependant, il enseigne et travaille aux États-Unis).
Trois dossiers à réviser
1. Cluster K-means
Les tâches de ce type concernent «l’apprentissage sans enseignant», lorsque nous devons décomposer les données initiales en un certain nombre de catégories connues à l’avance, mais que nous n’avons pas un certain nombre de «bonnes réponses», nous devons les extraire des données elles-mêmes. Le problème classique fondamental de trouver des sous-espèces de fleurs d'iris (Ronald Fisher, 1936!), Qui est considéré comme le premier signe de ce domaine de connaissances - est de cette nature.
La méthode est assez simple. Nous avons un ensemble d'objets représentés comme des vecteurs (ensembles de N nombres). Pour les iris, ce sont des ensembles de 4 chiffres caractérisant une fleur: la longueur et la largeur des lobes externes et internes du périanthe, respectivement (
Iris Fisher - Wikipedia ). En tant que distance ou mesure de proximité entre les objets, la métrique cartésienne habituelle est choisie.
De plus, les centres des grappes sont sélectionnés arbitrairement (ou non arbitrairement, voir ci-dessous), et les distances de chaque objet aux centres des grappes sont calculées. Chaque objet de cette étape d'itération est marqué comme appartenant au centre le plus proche. Ensuite, le centre de chaque groupe est transféré à la moyenne arithmétique des coordonnées de ses membres (par analogie avec la physique, il est également appelé le "centre de masse"), et la procédure est répétée.
Le processus converge assez rapidement. Dans les images en deux dimensions, cela ressemble à ceci:
1. La distribution aléatoire initiale des points sur le plan et le nombre de clusters

2. Définition des centres de clusters et affectation de points à leurs clusters
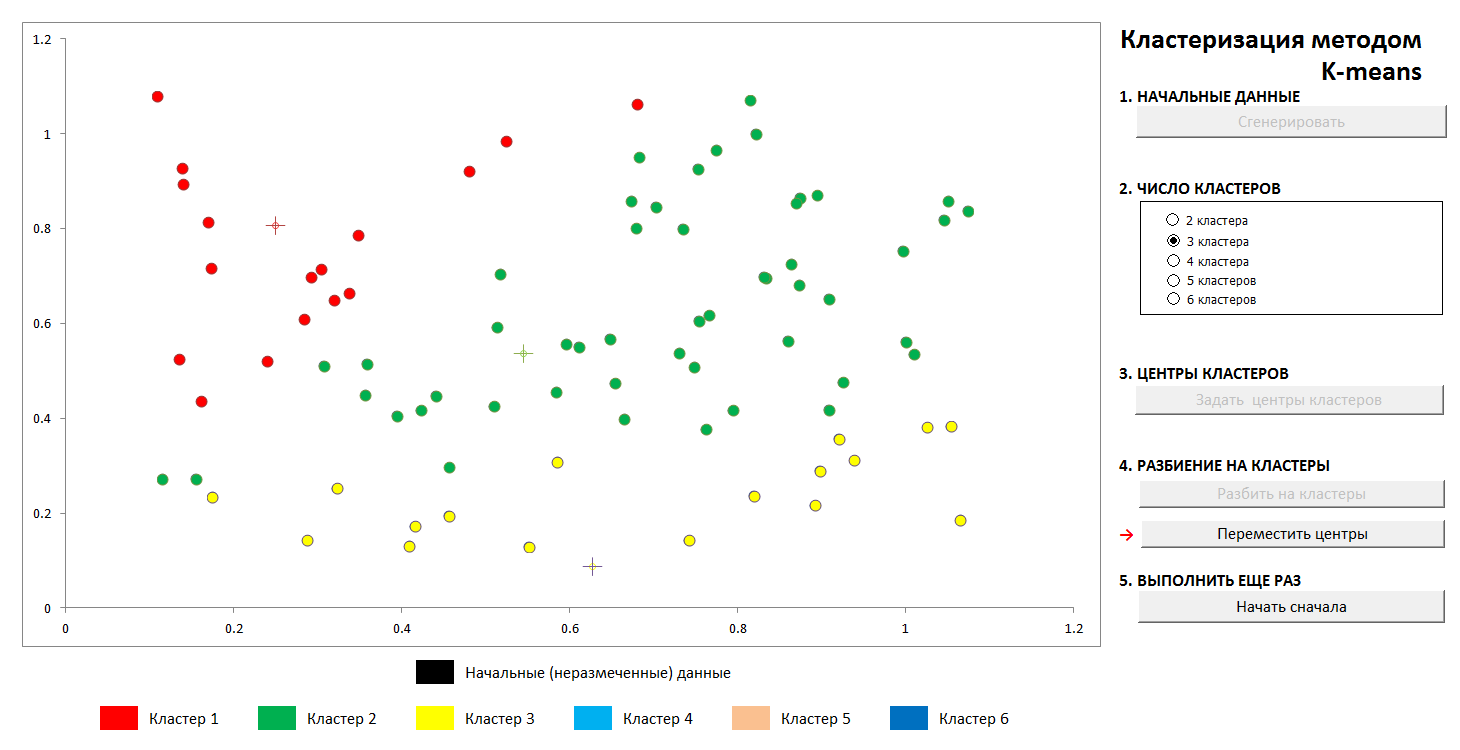
3. Transfert des coordonnées des centres de clusters, recalcul des points, jusqu'à stabilisation des centres. La trajectoire du centre de l'amas vers la position finale est visible.

À tout moment, vous pouvez définir de nouveaux centres de cluster (sans générer une nouvelle distribution de points!) Et voir que le processus de partitionnement n'est pas toujours unique. Mathématiquement, cela signifie que pour la fonction optimisée (la somme des carrés des distances des points aux centres de ses grappes), nous trouvons non pas un minimum global, mais un minimum local. Ce problème peut être vaincu soit par un choix non aléatoire des centres initiaux des grappes, soit en triant les centres possibles (parfois il est avantageux de les placer exactement à un moment donné, alors au moins il y a une garantie que nous n'obtiendrons pas de grappes vides). Dans tous les cas, un ensemble fini a toujours une limite inférieure exacte.
Vous pouvez jouer avec ce fichier sur ce lien (n'oubliez pas d'activer le support des macros. Les fichiers sont vérifiés pour les virus)
Description de la méthode Wikipedia - Méthode
K-means2. Approximation par polynômes et ventilation des données. Recyclage
Un remarquable scientifique et vulgarisateur de la science des données K.V. Vorontsov parle brièvement des méthodes d'apprentissage automatique comme de "la science du dessin de courbes à travers des points". Dans cet exemple, nous trouverons le motif dans les données par la méthode des moindres carrés.
La technique de division des données source en «formation» et «contrôle», ainsi qu'un phénomène tel que le recyclage ou le «recyclage» des données sont présentés. Avec une approximation correcte, nous aurons une certaine erreur sur les données d'entraînement et une erreur légèrement plus grande sur les données de contrôle. Si c'est faux, c'est un ajustement exact des données d'entraînement et une énorme erreur sur le contrôle.
(C'est un fait bien connu que grâce à N points, il est possible de dessiner une seule courbe du N-1er degré, et cette méthode ne donne généralement pas le résultat souhaité. Le
polynôme d'interpolation de Lagrange sur Wikipedia )
1. Nous fixons la distribution initiale

2. Divisez les points en «formation» et «contrôle» dans un rapport de 70 à 30.

3. On trace une courbe d'approximation pour les points d'entraînement, on voit l'erreur qu'elle donne sur les données de contrôle

4. Nous dessinons la courbe exacte à travers les points d'entraînement, et nous voyons une erreur monstrueuse sur les données de contrôle (et zéro sur l'entraînement, mais quel est le point?).

Bien entendu, la variante la plus simple avec une seule partition en sous-ensembles «formation» et «contrôle» est représentée, dans le cas général, cela se fait de façon répétée pour le meilleur ajustement des coefficients.
Le fichier est disponible ici, anti-virus vérifié. Activez les macros pour fonctionner correctement
3. Descente de gradient et dynamique d'erreur
Il y aura un cas à 4 dimensions et une régression linéaire. Les coefficients de régression linéaire seront déterminés par étapes par la méthode de descente en gradient, initialement tous les coefficients sont des zéros. Un graphique séparé montre la dynamique de la réduction des erreurs à mesure que les coefficients sont de plus en plus finement réglés. Il est possible de voir les quatre projections bidimensionnelles.
Si vous définissez un pas de descente trop grand, il est clair que chaque fois que nous sauterons le minimum et que nous arriverons au résultat dans un plus grand nombre de pas, bien qu'à la fin nous arriverons quand même (à moins que nous ne touchions trop au pas de descente, alors l'algorithme ira " dans l'espacement "). Et le graphique de la dépendance de l'erreur sur l'étape d'itération ne sera pas lisse, mais «saccadé».
1. Générez des données, définissez le pas de descente du gradient
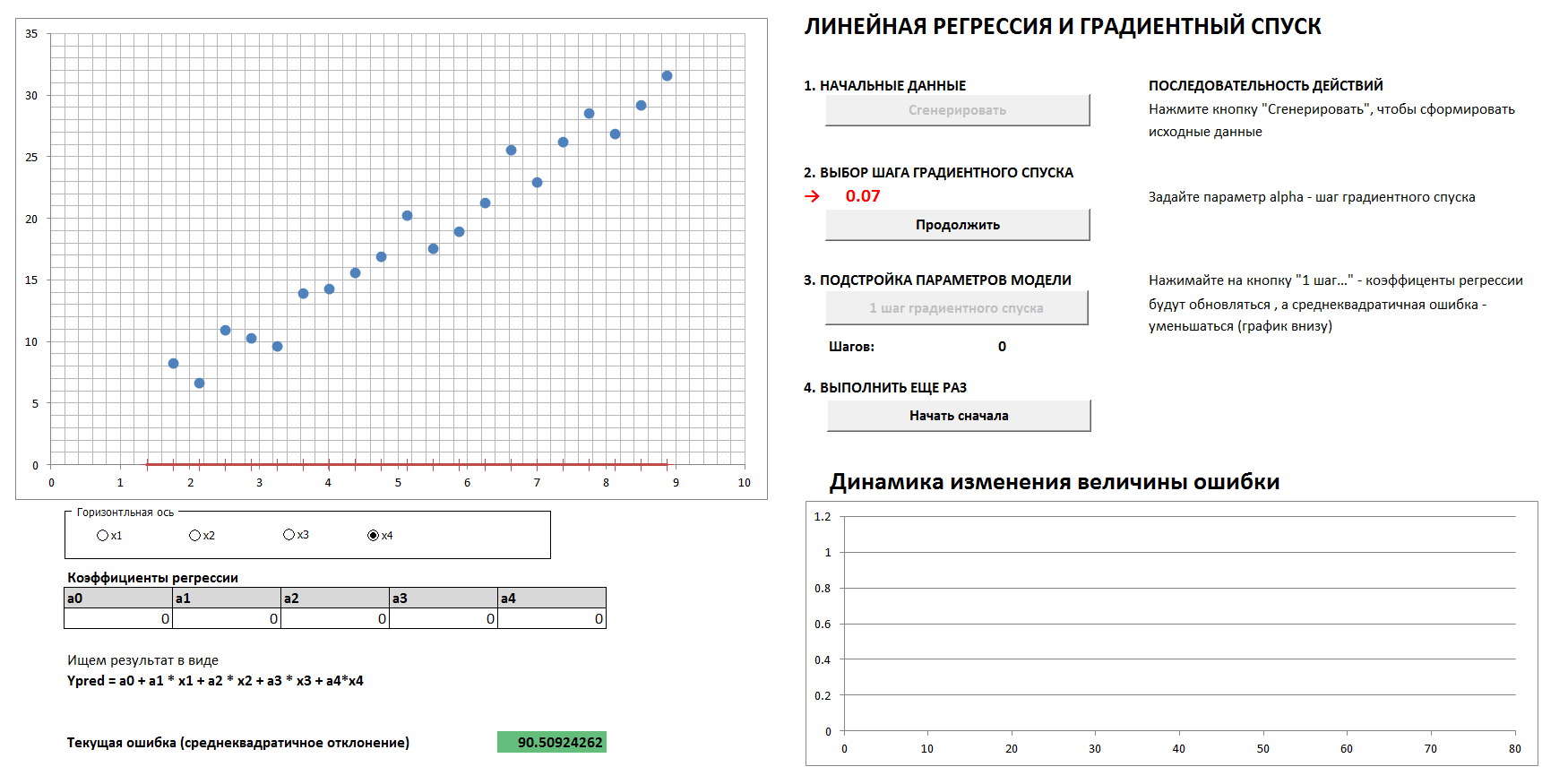
2. Avec le bon choix de l'étape de descente du gradient, nous arrivons au minimum en douceur et rapidement

3. Si l'étape de descente du gradient n'est pas sélectionnée correctement, nous sautons le maximum, le graphique d'erreur est "saccadé", la convergence prend un plus grand nombre d'étapes

et

4. Avec une sélection complètement incorrecte du pas de descente du gradient, nous nous éloignons du minimum

(Pour reproduire le processus avec les valeurs de l'étape de descente de gradient montrées dans les images, cochez la case "données de référence").
Fichier - par ce lien, vous devez activer les macros, il n'y a pas de virus.Selon une communauté respectée, une telle simplification et méthode de présentation est-elle acceptable? Dois-je traduire l'article en anglais?