Il est difficile de repenser le concept d'une tâche, mais le résultat en vaut la peine
 Note de l'auteur
Note de l'auteur : je sais que j'ai mal calculé le transfert de Bragg dans les cas classiques et quantiques; cependant, il est assez proche de la vérité pour comprendre la différence entre la programmation d'ordinateurs classiques et quantiques.
Heure: quelque part en 2018. Emplacement: canal pourri à Slaka.
"Connaissez-vous Python?"
Les questions de John Timmer, directeur scientifique d'Ars Technica, peuvent parfois être prises par surprise. S'il était possible d'imprégner des lettres à Slaka avec prudence, ma réponse «Oui» serait tout simplement suintante.
Il s'avère que D-Wave a décidé de donner au monde l'accès à son optimiseur quantique via l'API. Ars l'a invité à essayer, mais il fallait connaître Python. J'étais prêt pour ça.
J'ai supposé que D-Wave libérerait une sorte d'API fantastique qui pourrait prendre mon code propriétaire qui fait pleurer les programmeurs et le transformer en lignes optimisées quantiquement. Hélas, quand je suis arrivé à l'optimiseur quantique, il s'est avéré que ce n'était pas le cas. Je me suis rapidement retrouvé plongé dans la documentation, essayant de comprendre ce que je devais faire.
Je pense que le représentant des relations publiques de D-Wave avait en tête une personne qui en savait assez pour exécuter des exemples tout faits. Mais je suis têtu. Je devais trouver trois ou quatre tâches possibles que je voulais tester. Je voulais savoir: puis-je maîtriser le processus de résolution de ces problèmes sur un ordinateur D-Wave? Est-il facile de faire un saut conceptuel de la programmation classique à l'utilisation du recuit quantique? Est-ce qu'au moins certaines de mes tâches conviendront à cette machine?
Révélant une conclusion étonnante tout de suite, je dirai que les réponses étaient les suivantes: ce n'est peut-être pas tout à fait du «mastering»; difficile; pas toutes les tâches.
Choix des tâches de programmation
Malgré la façon dont vous m'imaginez, je peux être appelé un programmeur pratiquant. Essentiellement, toute personne ayant une bonne compréhension de la programmation grimacerait (et pourrait commettre un meurtre) après avoir vu mon code Python.
Cependant, je peux proposer des tâches qui nécessitent d'écrire un programme pour les résoudre. J'ai besoin, par exemple, de quelque chose qui calcule le champ électrique d'un ensemble d'électrodes. Quelque chose qui trouve un état avec une énergie d'atome d'hélium minimale. Ou quelque chose qui compte l'augmentation de l'intensité lumineuse au début du laser. Ces tâches m'intéressent le plus. Et en commençant ce projet, je ne savais pas si l'architecture D-Wave pouvait résoudre ces problèmes.
J'ai choisi deux problèmes qui, à mon avis, pourraient fonctionner: trouver des membres de l'ensemble de Mandelbrot et calculer les contours potentiels d'un ensemble d'électrodes. L'avantage de ces problèmes était que je pouvais les résoudre rapidement en utilisant le code classique et comparer les réponses. Mais j'ai rapidement rencontré des problèmes en essayant de comprendre comment commencer à résoudre ces problèmes sur une machine de D-Wave. Cela nécessite un changement majeur dans la compréhension des tâches, et ma pensée fonctionne très simplement.
Par exemple, l'un des problèmes que j'ai rencontrés est que nous avons affaire à des nombres binaires de bas niveau (malgré le fait qu'ils sont exprimés sous forme de qubits, pas de bits). Cela signifie qu'en fait, le programme n'a pas de types. Presque toute mon expérience en programmation a consisté à résoudre des problèmes physiques à l'aide de types numériques à virgule flottante.
Vous devez penser différemment à la tâche: la réponse doit être exprimée sous la forme d'un nombre binaire (idéalement, vrai ou faux), et toute la physique (par exemple, tous les nombres à virgule flottante) doit être exprimée par une combinaison de qubits. Même si ma vie en dépendait, je ne serais pas en mesure de comprendre comment cela peut être fait pour aucune de mes tâches. Immergé dans l'enseignement, j'ai laissé ce problème bouillir un peu dans mon propre jus.
Six mois plus tard, j'ai finalement rencontré un problème que je connaissais et que je pouvais résoudre avec un ordinateur D-Wave. Le passage de la lumière à travers un réseau de Bragg à fibres peut s'exprimer comme un problème binaire: un photon est-il sorti du filtre ou non? Toute la physique est contenue dans des composés qubit, et la réponse est extraite de l'énergie de la solution.
Caillebotis de Bragg
Un réseau de Bragg unidimensionnel est un matériau multicouche. Chaque espace entre les deux couches reflète une petite quantité de lumière. La pénétration totale à travers toute la structure est déterminée par la distance entre les interstices. Pour que la lumière passe, il faut que les ondes de différents intervalles s'additionnent en phase. Le spectre de passage d'un réseau de Bragg idéal avec 50 couches et une réflectance de 0,1% est indiqué ci-dessous.
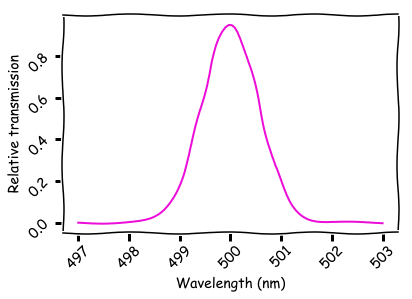
Le code suivant génère des données pour ce graphique:
ld = np.linspace(ld_center-3e-9, ld_center+3e-9, num_ld) k = 2*np.pi/ld T = np.ones(ld.shape) for j in range(num_layers): T = T*(1-A)*np.cos(j*k*layer_sep)**2
Ici, nous calculons explicitement les contributions relatives de chaque espace, exprimées en puissance optique, qui atteignent l'espace suivant. Les interférences constructives et destructrices sont prises en compte en réduisant ou en augmentant la contribution de l'écart, en fonction de la distance entre les couches coïncide avec la moitié de la longueur d'onde.
Ce hack est nécessaire car la connexion des qubits s'exprime uniquement en nombres réels et non en nombres complexes (la physique s'exprime mieux par des nombres complexes contenant l'amplitude et la phase de la lumière). Néanmoins, la sortie du code classique semble approximativement correcte - l'absence de bandes de fréquences latérales inquiète un peu, ce qui indique l'incomplétude du modèle, mais jusqu'à présent, cela n'a pas d'importance.
Le code du modèle classique manque de contrôles de cohérence. J'ai calculé le résultat, suggérant exactement comment l'onde se propagerait. Même si cette hypothèse s'avère incorrecte, le résultat du calcul sera le même - bien que toutes les équations soient basées sur la physique, il est impossible de garantir dans le code qu'elles le décrivent correctement.
On passe aux quanta
Dans le système D-Wave, il est nécessaire de créer une chaîne de qubits, chacun représentant l'intensité lumineuse dans l'espace. Chaque qubit est associé à ses voisins, et le poids de la connexion représente le passage d'un espace à l'autre, en tenant compte de la distance entre les interfaces. Si la distance entre les interfaces est égale à la moitié de la longueur d'onde, la lumière peut résonner entre les deux interfaces et passer. Si la distance est d'un quart de la longueur d'onde, une interférence destructrice est déclenchée et la connexion doit être minimale.
Le passage à travers un écart est indiqué à 99,9%, donc la connexion entre le zéro et les premiers qubits est
Entre le premier et le deuxième:
Entre le deuxième et le troisième:
Dans cette formule, d est la distance physique entre les couches et λ est la longueur d'onde. Si d / λ = 0,5, alors le cosinus est égal à l'unité, et nous pouvons espérer la transmission idéale de la lumière.
Dans le système D-Wave, cela signifie que tous les deux qubits voisins doivent être connectés comme suit:
Dans cette expression, le degré u prend en compte l'influence des qubits précédents et simplifie le schéma de connexion.
Mise en œuvre des tâches
Maintenant, sachant comment connecter les qubits, nous devons examiner la connexion physique des qubits pour décider comment terminer cette tâche. C'est ce qu'on appelle une intégration mineure.
Nous devons donner à l'ordinateur une liste des connexions entre les qubits avec leurs poids. Il faut également préciser les écarts indiquant l'importance de chaque qubit. Dans notre cas, tous les qubits sont également importants, ils sont donc définis comme -1 pour tous les qubits (j'ai pris ce nombre dans l'exemple standard). Les écarts et les connexions doivent être associés aux qubits physiques et aux relations entre eux. Dans le cas de tâches volumineuses, la recherche d'un tel mappage peut prendre beaucoup de temps.
Le code pour générer des relations et des écarts est assez simple.
Heureusement, l'API D-Wave essaiera de trouver seule une petite implémentation. J'ai trouvé que cela fonctionnait pour un filtre avec 50 couches, mais ne pouvait pas faire face à 100 couches. Cela me semble assez étrange, car ayant 2 000 qubits et une longueur de chaîne de 1 (nous n'avons pas besoin de combiner plusieurs qubits physiques pour en créer un logique), le système doit être capable d'implémenter des problèmes encore plus importants. Avec le recul, je pense que l'échec est dû au fait que j'ai demandé trop de connexions zéro.
Une autre approche consiste simplement à ne pas définir explicitement les liaisons nulles. Cela donne à l'algorithme la liberté de trouver plus d'options d'implémentation où les qubits n'ont pas de connexions. Je n'ai pas essayé cela, mais cette option me semble la prochaine étape logique.
Dans tous les cas, le démarrage de la machine D-Wave est très simple:
response = EmbeddingComposite(DWaveSampler()).sample_qubo(Q_auto, num_reads=num_runs)
Apprendre à parler cubiquement
La différence entre mon algorithme classique et la solution D-Wave est que l'ordinateur D-Wave ne renvoie pas directement un résultat clair. Il se révèle divisé en plusieurs parties. Nous obtenons une liste d'énergies, et la plus petite d'entre elles devrait être la solution. Pour plusieurs courses (disons 1000) pour chaque énergie, nous obtenons le nombre de fois qu'elle est apparue dans la réponse. Et pour chaque exécution, nous obtenons une «réponse», la valeur des qubits. Il n'était pas immédiatement clair pour moi laquelle de ces valeurs peut (et peut) être interprétée comme passant par un filtre.
Au final, j'ai décidé que l'énergie minimale de la solution serait la meilleure réponse, car cette valeur représente en quelque sorte la quantité d'énergie stockée dans le filtre. Par conséquent, une solution avec une énergie plus élevée représente une plus grande perméabilité du filtre, comme indiqué ci-dessous. Transformer cette réponse en un véritable passage de lumière reste un devoir pour ceux qui comprennent cela.

Il est également possible d'obtenir une représentation physique du processus en examinant les valeurs des qubits dans une solution avec l'énergie la plus faible. Ci-dessous, vous pouvez voir les valeurs binaires des solutions correspondant au pic de la courbe de transmission (500 nm), 50% de transmission (500,6 nm) et 5% de transmission (501,4 nm).
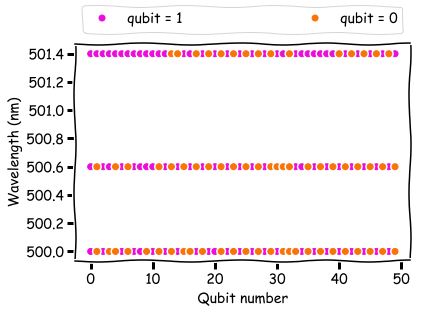
Au bord du pic de transmission, les qubits ont tendance à s'accumuler en groupes d'unités. Au sommet, les qubits alternent entre 0 et 1. Cette dernière solution est une image binaire de la façon dont l'intensité lumineuse dans le réseau de Bragg varie. En d'autres termes, la solution D-Wave présente également directement la physique, ce qui ne peut pas être dit de mon code classique.
C'est la vraie force du recuit quantique. Oui, je peux parfaitement dériver la courbe de passage à travers le filtre à partir de calculs classiques. Mais pour obtenir une image de ce qui se passe réellement à l'intérieur, vous avez besoin d'un code plus complexe. Et dans le recuit quantique, c'est totalement gratuit. À mon avis, c'est très cool.
Un autre avantage du recuit quantique est qu'il garantit une solution cohérente dans le cadre de mon choix de poids d'obligations qubit. Cela signifie que la solution d'un ordinateur quantique est susceptible d'être plus fiable que la solution obtenue à partir du code classique.
Discussions sur la programmation quantique
La partie la plus difficile de la programmation d'une machine D-Wave est que vous devez penser différemment aux tâches. Par exemple, je me suis habitué à minimiser les problèmes lorsque la courbe coïncide avec les données. Mais j'ai trouvé très difficile de changer votre façon de penser à un problème physique afin de commencer à écrire du code pour le résoudre. Cela n'aide pas que la plupart des exemples donnés par la société me semblent abstraits et ne s'adaptent pas aux problèmes physiques. Mais cette situation va changer lorsque de plus en plus d'utilisateurs commenceront à publier leur code.
De plus, des difficultés peuvent survenir avec l'interprétation de la réponse. Fondamentalement, j'ai aimé la simplicité de l'API, et c'est génial d'avoir des idées supplémentaires gratuitement. Dans un avenir proche, je pourrais utiliser D-Wave pour résoudre de vrais problèmes.